Способы улучшения цифровых сигналов в условиях ограниченного объема априорной информации

Содержание

Основная часть

Выводы

Библиографический список

В современных радиоэлектронных системах в процессе передачи сигнала на него накладываются различные шумы. Процесс приема и перевода сигнала в цифровой вид также сопряжен с внесением в сигнал шумовой составляющей. В большинстве случаев шум является аддитивным. Как правило, при обработке сигнала основной задачей является выделение полезной и ослабление шумовой составляющей. Для решения данной задачи чаще всего используются критерий минимума среднеквадратической погрешности или критерий среднеабсолютного отклонения. В связи с чем актуальной является задача обработки цифрового сигнала одновременно по нескольким критериям [1].

В связи с этим значительный интерес представляет использование многокритериальных методов обработки результатов измерений, представленных единственной реализацией при ограниченном объеме априорной информации о функциях полезной составляющей и шуме.

Цель работы тАУ уменьшение дисперсии шумовой составляющей многокритериальными методами сглаживания входного сигнала, представленного единственной реализацией нестационарного случайного процесса в условиях априорной неопределенности.

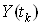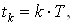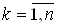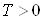Пусть исходные результаты измерений представляют собой дискретную последовательность значений измеряемой физической величины , полученную в равноотстоящие моменты времени Вагде Ва(Ва- константа). Данную выборку результатов измерений можно рассматривать как реализацию случайного процесса 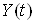, который является аддитивной смесью полезного сигнала и шума. Упрощенная математическая модель входного сигнала представляется в виде:

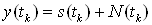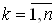, ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

где 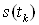ВатАУ полезная составляющая; 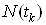ВатАУ аддитивная шумовая составляющая; 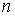ВатАУ объем выборки.

Функциональная зависимость от времени 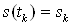Ваполезной составляющей неизвестна. Закон распределения аддитивного шума 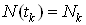Ватакже считается априорно неизвестным. Однако предполагается, что плотность распределения шумовой составляющей имеет нормальный закон, а математическое ожидание равно нулю.

Получение оценки 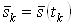Вавеличины 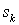Ваможно интерпретировать как уменьшение дисперсии аддитивного шума 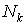. Предлагается уменьшать дисперсию измеряемого процесса путем существенного уменьшения суммы квадратов конечных разностей его значений [2]:

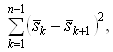ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)

а также (или) уменьшения суммы квадратов конечных разностей второго порядка:

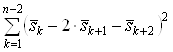.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)

При этом в качестве меры расхождения исходного и полезного сигналов используется сумма:

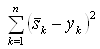.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)

Для определения оценок 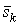Вабудем стремиться одновременно уменьшить суммы (2 и(или) 3) и (4). Эта цель достигается минимизацией двухкритериальных целевых функций вида [1тАУ3]:

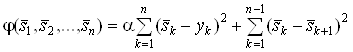,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)

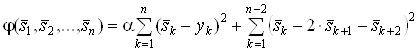,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6)

а также минимизаций трехкритериальной целевой функцией вида:

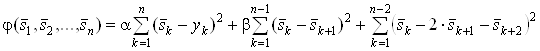,(7)

где 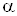Ваи 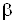ВатАУ постоянные регулировочные множители. При реализации рассматриваемых методов сглаживания наилучшие результаты на основе использования имитационного моделирования достигаются при значениях 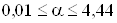Вав случае использования целевых функций вида (5) и (6) и 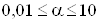, 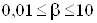Вав случае использования целевой функции вида (7).

Заметим, что целевые функции (6, 5тАУ7) непрерывны и ограничены снизу на множестве 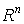, поэтому, по крайней мере, в одной точке 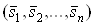Вадостигает своего наименьшего значения. Докажем единственность такой точки на примере целевой функции вида (5). В силу необходимого условия экстремума ее координаты должны удовлетворять системе уравнений:

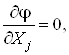
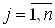,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)

то есть следующей системе 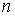Валинейных уравнений с 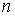Ванеизвестными

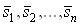:.ВаВаВаВаВаВа (9)

Перепишем систему (9) в виде:

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (10)

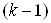Докажем, что система уравнений (10) имеет единственное решение. С этой целью методом математической индукции установим справедливость утверждения ВаВлпервые Вауравнений системы (10) задают переменные Вакак линейные функции аргумента 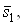Ват.е. 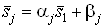, причем 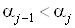, 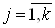В» при каждом 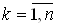Ва(полагаем здесь 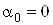). При 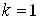Ваимеем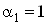 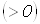, , 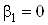а в случае 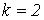ВатАУ 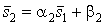, где 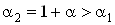, , 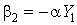то есть утверждения 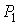, 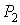Ваверны. В предположении верности утверждения 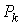Вапри некотором Вадокажем справедливость утверждения 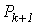. Из 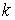-го уравнения системы (10) получаем

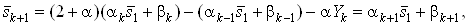
где ; .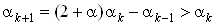

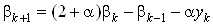Итак, утверждения Вавыполнены. С помощью утверждения 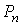Вапоследнее уравнение системы (10) приводится к виду 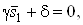Вагде 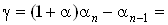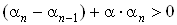, 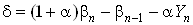. Полученное уравнение имеет единственное решение 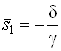, по которому однозначно определяются значения 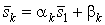, где .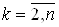

Таким образом, система уравнений (5) имеет единственное решение; аналогично доказательство единственности решения для целевых функций вида (6) и (7).

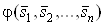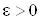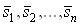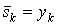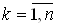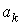Для нахождения точки наименьшего значения целевых функций Ва(5), (6) и (7) применим метод наискорейшего спуска [4]. Зададим точность , с которой будут найдены значения . В качестве начальной итерации примем , . При каждом Вазададим величину , присвоив ей значение левой части k-го уравнения систем (10).

Для целевой функции (6), получим:

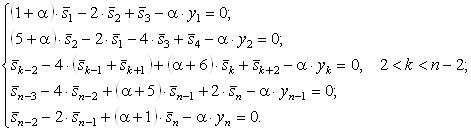ВаВаВаВаВаВаВаВа (11)

Целевая функция (7) сводится к решению системы:

(12)

Кроме того, для целевой функции вида (5) введем величину:

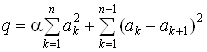.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (13)

Для целевой функции вида (6) тАУ величину:

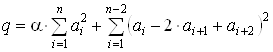.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (14)

Для целевой функции вида (7) тАУ величину:

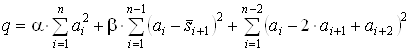.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (15)

Если 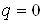, то в точке Вафункция Вадостигает наименьшего значения. Заметим, что 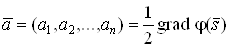Ваи что 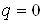Ватогда и только тогда, когда 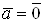. В случае 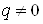Вафункция Ваявляется квадратичной функцией с положительной второй производной. Решив уравнение 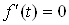, найдем точку минимума

тАУ для целевой функции вида (5):

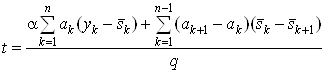,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (16)

тАУ для целевой функции вида (6):

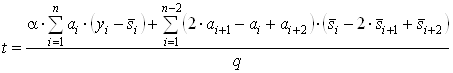,ВаВаВаВаВаВаВаВа (17)

тАУ для целевой функции вида (7):

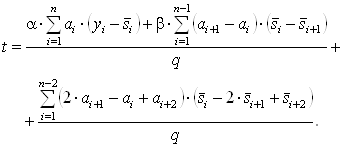ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (18)

Так как в точке 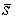Вапроизводная функции Вапо направлению вектора 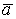Ваположительна, то 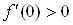; следовательно 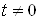. Произведем коррекцию значений :

, .

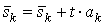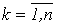После этого проверяем условие

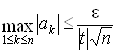.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (19)

Если неравенство (19) выполняется, требуемая точность считается достигнутой, и расчет заканчивается. Тогда 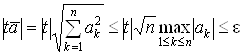, т.е. расстояние между двумя последними итерациями в пространстве 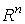Ване превосходит 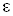. В случае невыполнения условия (19) повторяется расчет величин 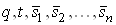Ваи проверка указанного условия.

Таким образом, вектор оценок Ваитерационно корректируется так, чтобы целевая функция 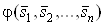Вадостигла своего наименьшего значения. На некотором шаге итерационного процесса выполнится условие (19), и вычисления прекращаются. Полученный вектор оценок Вас заданной точностью 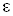Вабудет являться точкой наименьшего значения целевой функции 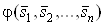Вапри заданных начальных условиях [5].

Также в работе предложено аналитическое решение двухкритериальной целевой функции вида (5). Как установлено ранее, точка минимума функции (5) является единственным решением системы линейных уравнений [2, 3]

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (20)

Покажем, что это решение имеет вид

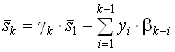, Ва,Ва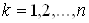ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (21)

где,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (22)

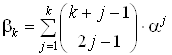ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (23)