Цифровая схемотехника
тАЮ ЦИФРОВАЯ СХЕМОТЕХНИКА тАЭ
ХАРЬКОВ 2006
СОДЕРЖАНИЕ
Предисловие
1 ЛОГИЧЕСКИЕ И СХЕМОТЕХНИЧЕСКИЕ ОСНОВЫ ЦИФРОВОЙ МИКРОСХЕМОТЕХНИКИ
1.1 Основные понятия алгебры логики
1.2 Логические элементы
1.3 Основные законы алгебры логики
1.4 Дизъюнктивные нормальные формы
1.5 Минимизация логических функций
1.6 Синтез комбинационных логических схем
2 КОМБИНАЦИОННЫЕ СХЕМЫ
2.1 Основные положения
2.2 Дешифраторы
2.3 Шифраторы
2.4 Демультиплексоры
2.5 Мультиплексоры
2.6 Арифметические устройства
3 ТРИГГЕРНЫЕ УСТРОЙСТВА
3.1 Основные понятия
3.2 Асинхронный RS-триггер
3.3 Синхронные триггеры
4 РЕГИСТРЫ
4.1 Общие сведения о регистрах
4.2 Регистры памяти
4.3 Сдвигающие регистры
4.4 Реверсивные регистры
4.5 Универсальные регистры
5 iЕТЧИКИ
5.1 Общие сведения о счетчиках
5.2 Счетчики с последовательным переносом
5.3 Счетчики с параллельным переносом
5.4 Реверсивные счетчики
5.5 Счетчики с произвольным коэффициентом счета не равным 2n
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРИ
ПРЕДИСЛОВИЕ
Данное методическое пособие содержит информацию, которая обеспечивает изучение дисциплин:
- ВлЦифровая схемотехникаВ» для студентов специальности 5.091504 (Обслуживание компьютерных и интеллектуальных систем и сетей);
- ВлМикросхемотехникаВ» для студентов специальности 5.090805 (Конструирование, производство и техническое обслуживание изделий электронной техники);
- ВлЭлектронные приборы и микроэлектроникаВ» для студентов специальности 5.090704 (Конструирование, производство и техническое обслуживание радиотехнических устройств).
Материал, который представлен в данной работе, предназначен для ознакомления студентов с основами современной цифровой микросхемотехники и включает основные виды цифровых устройств, которые широко используются и как самостоятельные изделия в виде микросхем малой и средней степени интеграции, и в составе микросхем высокой степени интеграции: микропроцессоров и микроконтроллеров.
Методическое пособие состоит из пяти разделов:
- логические и схемотехнические основы цифровой микросхемотехники,
- комбинационные схемы,
- триггерные устройства,
- регистры,
- счетчики.
Изложение материала построено таким образом, чтобы последовательно Влот простого к сложномуВ» представить основные теоретические принципы анализа и синтеза цифровых устройств. Каждый раздел содержит подразделы, в которых дается информация об условном графическом обозначении изучаемого устройства, приводится его таблица функционирования, функциональная или принципиальная схема и временные диаграммы работы там, где это требуется. Каждой из схем дается подробное описание логики ее работы с таким расчетом, чтобы каждый изучающий предмет освоил принципы анализа работы цифровых схем и приобрел необходимые навыки. Каждая из приведенных схем является типичной для данного устройства. При этом не исключается другая схемная реализация.
Основные понятия, определения, правила выделены ВлжирнымВ» шрифтом, чтобы сделать освоение предмета более удобным и наглядным.
Учитывая, что изложение материала проводится в порядке возрастания сложности изучаемых цифровых устройств и при этом каждая последующая тема базируется на материале предыдущей, целесообразно пользоваться данным методическим пособием в той последовательности, в которой расположены соответствующие разделы.
Данное пособие полезно использовать не только при изучении теоретических основ цифровой микросхемотехники, но и при подготовке к выполнению лабораторных работ, целью которых является углубление знаний и приобретение практических навыков по сборке и отладке цифровых устройств. Пособием можно пользоваться для самостоятельного изучения, а также при курсовом и дипломном проектировании.
1 ЛОГИЧЕСКИЕ и схемотехнические ОСНОВЫ ЦИФРОВОЙ МИКРОСХЕМОТЕХНИКИ
1.1 Основные понятия алгебры логики
Логика тАФ это наука о законах и формах мышления.
Математическая логика тАФ наука о применении математических методов для решения логических задач.
Все цифровые вычислительные устройства построены на элементах, которые выполняют те или иные логические операции. Одни элементы обеспечивают переработку двоичных символов, представляющих цифровую или иную информацию, другие тАФ коммутацию каналов, по которым передается информация, наконец, третьи тАФ управление, активизируя различные действия и реализуя условия их выполнения.
Электрические сигналы, действующие на входах и выходах названных элементов, имеют, как правило, два различных уровня и, следовательно, могут быть представлены двоичными символами, например 1 или 0. Условимся обозначать свершение какого-либо события (например, наличие высокого уровня напряжения в какой-либо точке схемы) символом 1. Этот символ называют логической единицей. Отсутствие какого-либо события обозначим символом 0, называемым логическим нулем.
Принято считать, что логическому нулю соответствует низкий уровень напряжения, а логической единице тАФ высокий.
Таким образом, каждому сигналу на входе или выходе двоичного элемента ставится в соответствие логическая переменная, которая может принимать лишь два значения: состояние логической единицы (событие истинно) и состояние логического нуля (событие ложно). Эти переменные называют булевыми по имени английского математика Дж. Буля, который еще в девятнадцатом столетии разработал основные положения математической логики. Обозначим логическую переменную символом х.
Различные логические переменные могут быть связаны функциональными зависимостями. Например, выражение у = f (x1, х2) указывает на функциональную зависимость логической переменной у от логических переменных х1 и х2, называемых аргументами или входными переменными.
Любую логическую функцию всегда можно представить в виде совокупности простейших логических операций. К таким операциям относятся:
- отрицание (операция ВлНЕВ»);
- логическое умножение (конъюнкция, операция ВлИВ»);
- логическое сложение (дизъюнкция, операция ВлИЛИВ»).
Отрицание (операция ВлНЕВ») - это такая логическая связь между входной логической переменной х и выходной логической переменной у, при которой у истинно только тогда, когда х ложно, и, наоборот, у ложно только тогда, когда истинно х. Изобразим данную функциональную зависимость в виде таблицы 1.1, которая называется таблицей истинности.
Таблица истинности - это таблица, отображающая соответствие всех возможных комбинаций значений двоичных аргументов значениям логической функции.
Таблица 1.1- Таблица истинности операции ВлНЕВ»
Логическая функция НЕ переменной у записывается как у =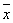 
Ваи читается Влу есть не хВ». Если, например, х - утверждение о наличии сигнала высокого уровня (логической единицы), то y соответствует утверждению о наличии сигнала низкого уровня (логического нуля).
Логическое умножение (конъюнкция, операция ВлИВ») - это такая функция, которая истинна только тогда, когда одновременно истинны все умножаемые переменные. Таблица истинности операции логического умножения соответствует таблице 1.2.
Таблица 1.2- Таблица истинности операции логического умножения
Операция ВлИВ» обозначается точкой (тАв). Иногда точка подразумевается. Например, операция ВлИВ» между двумя переменными х1 и х2 обозначается как у = х1 тАв х2.
Логическое сложение (дизъюнкция, операция ВлИЛИВ») тАУ это такая функция, которая ложна только тогда, когда одновременно ложны все слагаемые переменные. Таблица истинности операции логического сложения соответствует таблице 1.3. Операция ВлИЛИВ» обозначается знаком V. Например, у = x1 V х2.
Таблица 1.3 - Таблица истинности операции логического сложения
1.2 Логические элементы
1.2.1 Общие сведения о логических элементах
Логические элементы - это электронные схемы, реализующие простейшие логические функции.
Логические элементы, схематически представляются в виде прямоугольников, на поле которых изображается символ, обозначающий функцию, выполняемую данным элементом. ВаВаВаВаВаВаВаВа Например, на рисунке 1.1 показаны условные обозначения элементов, реализующих логические функции НЕ, И, ИЛИ, И- НЕ, ИЛИ- НЕ.
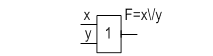
Рисунок 1.1-Условные обозначения логических элементов НЕ, И, ИЛИ, И-НЕ, ИЛИ-НЕ
Входные переменные принято изображать слева, а выходные тАФ справа. Считается, что передача информации происходит слева направо.
Если выходы одних элементов соединить со входами других, то получим схему, реализующую более сложную функцию. Совокупность различных типов элементов, достаточных для воспроизведения любой логической функции, назовем логическим базисом. Элементы И и НЕ представляют такой логический базис.
Логический базис может состоять всего лишь из одного типа элементов, например элемента типа И─НЕ, схема которого показана на рис. 1.2.
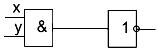
Рисунок 1.2- Схема получения элемента И-НЕ
Универсальность элемента И─НЕ обеспечила ему широкое применение при создании логических устройств цифровой вычислительной техники.
Существует и ряд других элементов, реализующих простейшие логические функции. К их числу, например, относится элемент суммирования по модулю два (исключающее ИЛИ), реализующий функцию неравнозначности двух переменных:
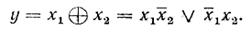
Таблица истинности и условное обозначение такого элемента показаны на рис. 1.3.
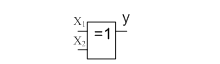
Рисунок 1.3 - Таблица истинности и условное обозначение элемента Влисключающее ИЛИВ»
Функция неравнозначности равна единице лишь в случае, когда переменные xl и х2 имеют разные значения.
1.2.2 Параметры логических элементов
Простейшие цифровые элементы характеризуются следующими параметрами:
-быстродействием tз ср ,
-нагрузочной способностью (коэффициентом разветвления по выходу) п,
-коэффициентом объединения по входу (числом входов логического элемента) т,
-помехоустойчивостью Un,
-потребляемой мощностью Рср,
-напряжением питания U,
-уровнем сигналов.
Быстродействие тАФ один из важнейших параметров, характеризуемый средним временем задержки распространения сигнала
tзср =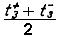 
,
где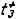 
Ваи 
Ва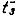тАФ задержки включения и выключения схемы (рисунок 1.4).
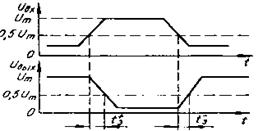
Рисунок 1.4-Задержки включения и выключения схемы
Нагрузочная способность показывает, сколько логических входов может быть одновременно подключено к выходу данного логического элемента без нарушения его работоспособности.
Коэффициент объединения по входу определяет максимально возможное число входов логического элемента. Увеличение т расширяет логические возможности схемы за счет реализации функции от большего числа аргументов на одном элементе ИтАФНЕ, ИЛИтАФНЕ и т. д., однако при этом ухудшаются быстродействие и помехоустойчивость.
Помехоустойчивость характеризует способность элемента правильно функционировать при наличии помех. Помехоустойчивость определяется максимально допустимым напряжением помехи, при котором обеспечивается работоспособность схемы.
Потребляемая мощность характеризуется средним значением
Рср = (Р0 + Р3 )/ 2 ,
где Р0 и Р3 потребляемые мощности в открытом и закрытом состояниях схемы. При этом считается, что в устройстве в каждый момент времени приблизительно половина схем открыта. Однако в устройствах, которые имеют сложный инвертор, потребляемая мощность зависит от частоты их переключений. Поэтому тут необходимо учитывать среднюю потребляемую мощность при максимально допустимой частоте следования переключающих импульсов и скважности, равной двум. При определении этой мощности усреднение проводят по полному периоду переключения схемы.
Логические элементы характеризуются еще количеством используемых источников питания и значениями напряжения питания, а также полярностью и уровнем входного и выходного сигналов.
1.2.3 Базовые схемы логических элементов
Из всего разнообразия схемотехнического и технологического построения цифровых схем наибольшее распространение получили две основные разновидности: ТТЛ и МОП-схемы.
1.2.3.1 Базовые интегральные ТТЛ-схемы
Основной особенностью элементов ТТЛ является использование в них многоэмиттерных транзисторов (МЭТ), которые реализует функцию ВлИВ». Базовые интегральные ТТЛ-схемы реализует функцию И-НЕ и имеют два вида выходов: с нагрузкой в коллекторе выходного транзистора VT4 (R3, VT3, VD) и с открытым коллектором. Оба варианта показаны на рисунках 1.5 и 1.6.
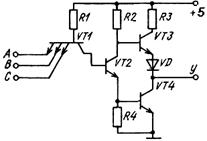
Рисунок 1.5-Базовая интегральная ТТЛ-схема с нагрузкой в коллекторе выходного транзистора
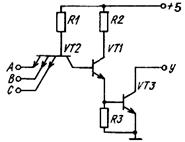
Рисунок 1.6-Базовая интегральная ТТЛ-схема с открытым коллектором
В схеме на рисунке 1.5 на транзисторах VT2тАФVT4 реализован сложный инвертор, осуществляющий операцию ВлНЕВ», что позволило обеспечить высокую нагрузочную способность, достаточное быстродействие и помехоустойчивость схемы. Кроме того, в выходной цепи отсутствует сквозной ток по цепи +5В через R3 тАУ VT3 тАУ VD тАУ VT4 тАУ общий провод, т.к. в любом состоянии закрыт один из транзисторов либо VT3, либо VT4.
Схема на рисунке 1.6 с открытым коллектором, позволяет иметь много параллельных выходов, что повышает нагрузочную способность схемы.
Рассмотрим принцип работы базовой ТТЛ-схемы (рисунок 1.5) для двух случаев, соответствующих различным наборам входных сигналов.
Случай 1. Если на все входы МЭТ VT1 поданы напряжения, соответствующие уровню логической единицы, то закрыты эмиттерные переходы VT1, и протекает ток через резистор R1, открытый коллекторный переход в базу транзистора VT2, открывая его. Теперь протекает ток через резистор R2, открытый VT2, а затем усиленный ток с эмиттера VT2 поступает в базу выходного инвертирующего транзистора VT4, открывая его до состояния насыщения, тем самым соединяя выход с общим проводом тАУ и напряжение на выходе У будет соответствовать уровню логического нуля. При этом транзистор VT3 будет закрыт, т.к. потенциал его базы не будет превышать 1В, что недостаточно для открывания VT3.
Действительно:
UбVT3 = UбэVT4 + UкэVT2 = 0,7 + 0,3 = 1В;
UэVT3 = UкэVT4 + UVD = 0,3 + 0,7 = 1В.
UбэVT3 = UбVT3 тАУ UэVT3 = 1 тАУ 1 = 0.
Случай 2. Если хотя бы на одном входе МЭТ VT1 появится входное напряжение, соответствующее уровню логического нуля, то откроется соответствующий переход база тАФ эмиттер VT1, МЭТ перейдет в состояние насыщения и потенциал его коллектора станет близким к нулю.
А точнее, если считать, что логический ноль не превышает 0,3В, а падение напряжения на открытом переходе база - эмиттер VT1 тАУ 0,7В, то потенциал базы VT1 будет не более, чем 0,3 + 0,7 = 1В. Следовательно, VT2 закроется, и закроется VT4, т.к. для их открывания необходимо по 0,7В и плюс 0,7В для открывания перехода база тАУ коллектор VT1. Итак, чтобы открыть цепочку VT2 - VT4 надо, чтобы на базе VT1 было не менее 0,7 + 0,7 + 0,7 = 2,1В, что соответствует первому случаю.
Транзистор VT3 откроется по следующей причине. Т.к. VT2 закрыт, то нет тока через R2 и соответственно падения напряжения на нем, поэтому потенциал на коллекторе VT2, а следовательно и на базе VT3, повысится до 5В. На выходе у схемы установится напряжение, соответствующее уровню логической единицы, которое поступает через открытый VT3 от +5В.
Кроме рассмотренных ТТЛ-схем, выпускаются схемы с тремя состояниями для обеспечения совместной работы с линиями магистралей (рисунок 1.7).
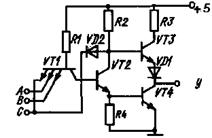
Рисунок 1.7- Базовая интегральная ТТЛ-схема с тремя состояниями
Название этих схем может ввести в заблуждение, так как на самом деле они не являются логическими элементами с тремя уровнями напряжений. Это самые обычные логические схемы, которые имеют третье состояние выхода тАФ ВлобрывВ». Они совмещают в себе все преимущества элементов с резистором в цепи нагрузки и способность работать на общую шину, которой обладает схема с открытым коллектором. Схемы с тремя состояниями имеют отдельный запирающий вход С (обычно он обозначается CS (Chip Select тАУ выбор кристалла), с помощью которого (при подаче на него логического нуля) они могут устанавливаться в третье состояние независимо от того, какие сигналы действуют на логических входах. Третье состояние характеризуется тем, что при этом закрыты оба транзистора VT3 и VT4, и выход не подсоединен ни к +5В, ни к общему проводу.
Ввиду улучшенных характеристик их используют обычно в качестве шинных формирователей вместо схем с открытым коллектором. Устанавливать нагрузочный резистор в этом случае не требуется.
1.2.3.2 Логические схемы на МОП-транзисторах
В настоящее время выпускается несколько разновидностей логических схем на МОП-транзисторах. Особенность ИМС на МОП-структурах состоит в том, что в этих схемах отсутствуют резисторы, а роль нелинейных резисторов выполняют соответствующим образом включенные транзисторы. Они имеют высокую нагрузочную способность и помехоустойчивость и занимают мало площади на поверхности кристалла, они технологичны и дешевы. МОП-транзисторы по принципу работы являются аналогами электронных ламп, так как управляются напряжением, а не током.
Схемы на МОП-транзисторах пока имеют меньшее быстродействие, чем схемы на биполярных транзисторах, что объясняется довольно значительными емкостями, образующимися между затвором, истоком, стоком и подложкой МОП-транзистора, на перезаряд которых требуется определенное время.
Наибольшее распространение получили КМОП-схемы (комплементарные МОП-схемы), в которых совместно применяются как п-канальные, так и р-канальные транзисторы.
Преимуществами схем на КМОП-транзисторах являются малая потребляемая мощность, высокое быстродействие и повышенная помехоустойчивость. В основе всех логических КМОП-схем лежит КМОП-инвертор (рисунок 1.8).
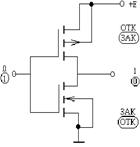
Рисунок 1.8 - КМОП-инвертор
3десь нижний транзистор с каналом n-типа, верхний тАФ с каналом р-типа. Затворы обоих транзисторов объединены, на них подается управляющее напряжение. Подложки соединены с истоками. При поступлении на вход напряжения высокого уровня (логической единицы) открывается транзистор с каналом n-типа (нижний), a с каналом р-типа (верхний) закрывается. На выходе тАУ сигнал логического нуля.
Наоборот, при подаче на вход напряжения, соответствующего уровню логического нуля, открывается верхний транзистор, a нижний закрывается. На выходе тАУ сигнал логической единицы.
Схема, реализующая функцию ИЛИтАФНЕ, показана на рисунке 1.9.
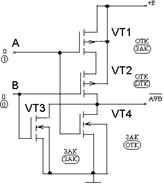
Рисунок 1.9 - Схема ИЛИтАФНЕ КМОП
При поступлении на вход А напряжения, соответствующего уровню логической единицы, открывается транзистор VT4 и закрывается VT1, в результате чего напряжение на выходе будет соответствовать уровню логического нуля. При подаче на входы A и В напряжения, соответствующего уровню логического нуля, транзисторы VT3 и VT4 закрываются, a VT1 и VT2 открываются. При этом напряжение на выходе будет соответствовать уровню логической единицы (т. е. близко к напряжению Е).
Схема, реализующая функцию ИтАФНЕ, изображена на рисунке 1.10.
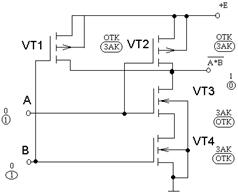
Рисунок 1.10- Схема ИтАФНЕ КМОП
К недостаткам КМОП-технологии следует отнести то, что здесь невозможно достичь столь же высокой плотности упаковки, как при МОП-техноологии из-за некоторой избыточности транзисторов. Однако в КМОП-схемах не протекает постоянно ток, что значительно снижает потребляемую мощность в статическом режиме. В динамическом режиме потребляемая мощность растет из-за перезаряда межэлектродных емкостей транзисторов и одновременного открывания всех транзисторов в момент их переключения, т. е. потребляемая мощность таких схем растет с повышением частоты переключения.
1.3 Основные законы алгебры логики
В алгебре логики приняты следующие основные законы:
- переместительный (свойства коммутативности)
x1 V х2 = х2V x1
x1 тАв х2 = х2 тАв x1
- сочетательный (свойства ассоциативности)
x1 V (х2 V x 3) = (x1 V х2 ) V x 3
x1 тАв (х2 тАв x 3) = (x1 тАв х2 ) тАв x 3
- распределительный (свойства дистрибутивности)
x1 V х2 тАв x 3 = (x1 V х2 ) (x1 V х3 )
x1 тАв ( х2 V x 3 ) = x1 тАв х2 V x1 тАв х3
- закон инверсии (правило де Моргана)
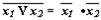
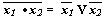
- закон склеивания
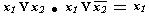
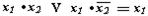
Переместительный и сочетательный законы встречается в обычной алгебре и не вызывает сомнения.
Распределительного закона для умноження и закона инверсии в обычной алгебре нет. Доказательство этих законов может быть выполнено посредством составления таблиц истинности для правой и левой частей уравнений, описывающих тот или иной закон.
Закон инверсии может быть использован для перехода от дизъюнкции к конъюнкции, и наоборот. Так, например, если применить инверсию к левой и правой частям выражений, отражающих закон инверсии, получим 
Ва, и далее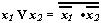 
Ва. Такое преобразование может понадобиться при проектировании логической схемы для перехода к базису И-НЕ.
В законе склеивания каждая пара объединяемых элементарных произведений различается лишь одной переменной (х2), которая входит в первое произведение без отрицания, а во второе тАФ с отрицанием. Такие элементарные произведения называют соседними. К соседним произведениям применим закон склеивания, в результате чего уменьшаются число суммируемых произведений и на единицу тАФ число переменных. Остается только та переменная, которая неизменна.
1.4 Дизъюнктивные нормальные формы
Для записи одной и той же функции алгебры логики можно использовать много различных форм. Формы, которые представляют суммы элементарных произведений, называют дизъюнктивными нормальными формами (ДНФ).
Элементарное произведение тАУ это такое произведение, в котором сомножителями являются только отдельные переменные или их отрицания.
Очевидно, одна и та же функция может быть представлена множеством различных ДНФ. Однако существуют такие виды ДНФ, в которых функция может быть записана единственным образом. Эти формы называют совершенными дизъюнктивными нормальными формами (СДНФ). СДНФ определяется как сумма элементарных произведений, в которых присутствуют все переменные либо с отрицанием, либо без него.
Правило записи СДНФ функции по ее таблице истинности:
Для всех комбинаций входных переменных, обращающих функцию в единицу, записать элементарные произведения, инвертируя переменные, равные в данной комбинации нулю, а все полученные элементарные произведения соединить знаками логического суммирования.
Рассмотрим пример. Пусть функция задана таблицей истинности (таблица 1.4). Требуется записать СДНФ функции по ее таблице истинности.
Таблица 1.4- Таблица истинности
| х2 | х1 | х0 | F(х2, х1, х0) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Вместе с этим смотрят:
GPS-навигация
IP-телефония. Особенности цифровой офисной связи
РЖсторiя звтАЩязку та його розвиток
Автоматика, телемеханика и связь
Анализ режимов автоматического управления