Исследование переходных процессов
Кузнецкий институт информационных и управленческих технологий
(филиал ПГУ)
Курсовая работа
по дисциплине тАЬТОЭ тАЭ
специальности 200100
ВлМикроэлектроника и твердотельная электроникаВ»
на тему: Исследование переходных процессов
2009 г.
Содержание
1. Краткие теоретические сведения
2. Расчет переходного процесса классическим методом
3. Расчет переходного процесса операторным методом
4. Построение графика в имитационном режиме WorkBench
Заключение
Список литературы
1. Краткие теоретические сведения
В соответствии со структурной схемой выполнения курсовой работы на первом этапе производится расчет переходных процессов в электрических цепях со сосредоточенными параметрами и определяется напряжение на одном из элементов схемы, т.е. происходит формирование сигнала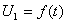 на половине периода
на половине периода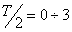 τ maх.
τ maх.
По заданному варианту выбирается электрическая схема, параметры этой схемы, а также определяется искомое напряжение на отдельном элементе схемы. Во всех схемах действует постоянная ЭДС. Необходимо на 1 этапе получить закон изменения во времени искомого напряжения после коммутации. И на основании полученного аналитического выражения построить график изменения 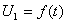 Вана интервале времени от 0 до 3 τ max.
Вана интервале времени от 0 до 3 τ max.
Переходные процессы в линейных электрических цепях описываются линейными дифференциальными уравнениями. Решение таких уравнений представляет собой сумму двух решений: частного и общего.
При этом частное решение (принужденная составляющая) определяется напряжением на элементе в установившемся режиме ( t → ∞) - 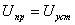 . Общее решение (свободная составляющая напряжения) зависит от вида корней характеристического уравнения, которые могут быть:
. Общее решение (свободная составляющая напряжения) зависит от вида корней характеристического уравнения, которые могут быть:
В· вещественными различными,
В· вещественными равными,
В· комплексно-сопряженными.
Соответственно этим трем видам корней решение для свободной составляющей напряжения приводится к виду:
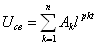 ;
;
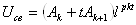 ;
;
 .
.
Где введены обозначения:
В· n-число корней характеристического уравнения (для рассматриваемых схем n = 2)
В· k- номер корня характеристического уравнения
В· 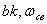 - соответственно-вещественная и мнимая части комплексно-сопряженных корней (
- соответственно-вещественная и мнимая части комплексно-сопряженных корней (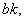 - характеризует затухание переходного процесса,
- характеризует затухание переходного процесса, 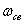 - частоту свободных колебаний переходного процесса).
- частоту свободных колебаний переходного процесса). 
В· 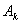 - постоянные интегрирования, определяемые из начальных условий.
- постоянные интегрирования, определяемые из начальных условий.
В· pk- тАЬkтАЭ- корень характеристического уравнения.
При определении начальных условий используются законы коммутации и уравнения цепи, составленные по первому и второму законам Кирхгофа для схемы после коммутации.
Различают два закона коммутации:
1. Ток в ветви с индуктивным элементом в момент коммутации 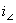
 Варавен току в этой ветви до коммутации
Варавен току в этой ветви до коммутации 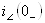 :
:
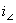
 Ва=
Ва= 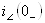 ;
;
2. Напряжение на емкостном элементе в момент коммутации 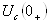 Варавно напряжению на этом элементе до коммутации
Варавно напряжению на этом элементе до коммутации 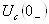 :
:
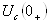 Ва=
Ва= 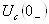 .
.
С учетом изложенного алгоритма расчета переходного процесса классическим методом имеет вид:
1. Рассчитывается электрическая схема до коммутации, и определяются независимые начальные условия 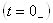 .
.
2. После коммутации по законам коммутации определяются:
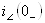 ,
, 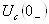 ;
;
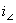
 Ва=
Ва= 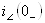 ;
;
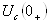 Ва=
Ва= 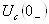 .
.
3. Определяют искомое напряжение на элементе в установившемся режиме 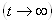 . Для этого электрическую цепь рассчитывают методом расчета электрических цепей постоянного тока. При этом учитывают
. Для этого электрическую цепь рассчитывают методом расчета электрических цепей постоянного тока. При этом учитывают 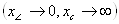 .
.
4. Составляют характеристическое уравнение электрической цепи для схемы после коммутации. В простых цепях это уравнение получают с помощью входного сопротивления цепи в комплексной форме: 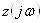 . Заменяя
. Заменяя 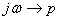 Ва- получаем характеристическое уравнение: z(p)=0. Решая это уравнение находят корни (
Ва- получаем характеристическое уравнение: z(p)=0. Решая это уравнение находят корни (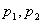 ).
).
5. Составляют в общем виде решение дифференциального уравнения описывающее переходный процесс
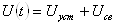 .
.
6. Для нахождения постоянных интегрирования переходного процесса составляется система уравнений по законам Кирхгофа для схемы в момент коммутации 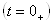 . А также учитываются законы коммутации из п.I алгоритма. ВаИз уравнений находится зависимое начальное условие искомого напряжения, и для момента времени t=0 и зависимых и независимых начальных условий тАУ определяются постоянные интегрирования.
. А также учитываются законы коммутации из п.I алгоритма. ВаИз уравнений находится зависимое начальное условие искомого напряжения, и для момента времени t=0 и зависимых и независимых начальных условий тАУ определяются постоянные интегрирования.
7. В соответствии с полученными корнями характеристического уравнения и найденными постоянными интегрирования составляется решение искомого напряжения в аналитической форме:
7.1. Корни вещественные различные: 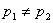
 ;
;
7.2. Корни вещественные равные: 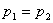
 ;
;
7.3. Корни комплексно-сопряженные:

8. На основании полученного аналитического выражения строят график  Вав интервале времени от
Вав интервале времени от 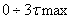 , при этом постоянные времени определяют по формулам
, при этом постоянные времени определяют по формулам
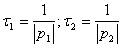 .
.
2. Расчет переходного процесса классическим методом
В цепи, питаемой от источника постоянной ЭДС, размокнут ключ. Необходимо найти напряжение на конденсаторе после коммутации при следующих параметрах элементов схемы:
E=120 B
L=10 мГн;
С=10 мкФ;
R1=20 Ом;
R2=80 Ом;
R3=1000Ом;
R4=1000Ом.
1. Нужно определить искомое напряжение 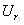 Ваклассическим методом. Мы видим, что
Ваклассическим методом. Мы видим, что . Поэтому ищем
. Поэтому ищем 
Чтобы найти решение свободной составляющей, составим характеристическое входное сопротивление. При этом индуктивностям приписываем сопротивление pL, а емкостям 1/pC.
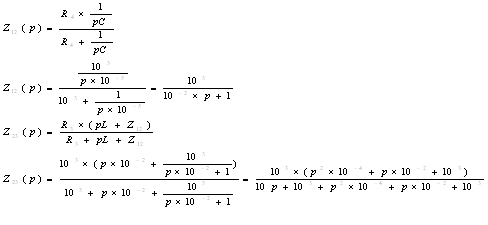

Корни действительные и различные.
Свободная составляющая напряжения на конденсаторе.
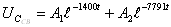
Независимые начальные условия:

По законам Киркгофа:
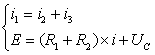
В начальный момент времени (после коммутации)
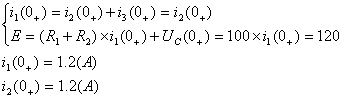
т.к. 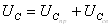
Установившееся значение тока i3пр неизменно следовательно на L нет падения напряжения, и схема выглядит так:
Вот и видим, что Ur3(f)=Uc(f)
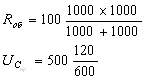
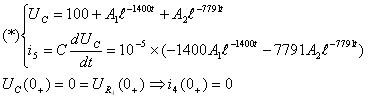
Для узла 3: 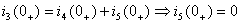
Тогда (*) для момента 0+:
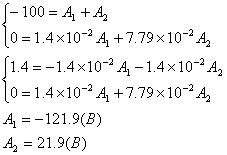
Искомое напряжение:
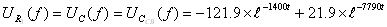
Изобразим на миллиметровой бумаге график переходного процесса.
3.Расчет переходного процесса операторным методом
Находим операторное сопротивление цепи:
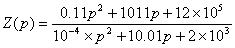
Так как операторные сопротивления записываются точно также, как и сопротивления для тех же цепей в комплексной форме, где 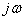 Вазаменяется на p (т.е. все как для Zвх из пункта 1.)
Вазаменяется на p (т.е. все как для Zвх из пункта 1.)
I1(p)-изображение тока, через изображение входного сопротивления
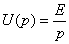
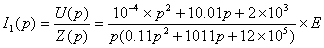
Изображение напряжения на R3 изображению напряжения на конденсаторе:
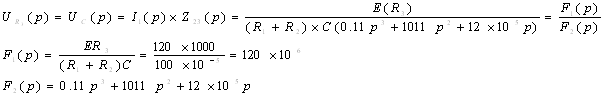
По формуле разложения от изображений к аригеналам переход такой:

Свободная составляющая.
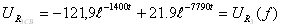
 4. Построение графика в имитационном режиме WorkBench:
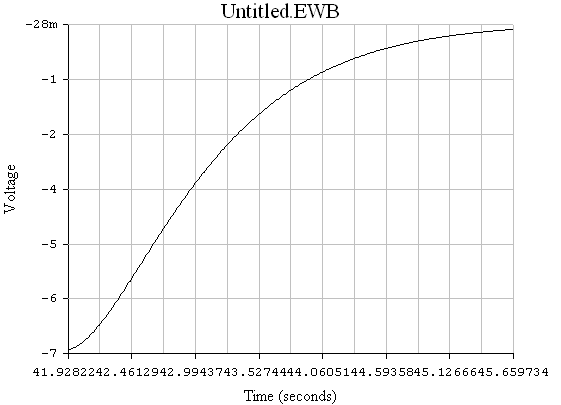
4. Построение графика в имитационном режиме WorkBench:
Заключение
В результате выполнения курсовой работы был исследован переходной процесс в некоторой схеме. Расчет производился двумя методами: классическим и операторным. В итоге функция напряжения на R3, найденная операторным методом, сошлась с функцией напряжения классического метода. Это свидетельствует о правильности выполнения расчетов и курсовой работы в целом. переходный электрический цепь напряжение
Список используемой литературы
1. Бессонов Л.А. Теоретические основы электротехники. М:Высшая школа, 1999, - 786с.
2. Ашанин В.Н, Герасимов А.И., Чепасов А.П. Анализ передачи сигнала в линейных электрических системах .Методические указания к выполнению курсовых работ. Пенза, ПГУ, 2000г.
Вместе с этим смотрят:
GPS-навигация
IP-телефония. Особенности цифровой офисной связи
РЖсторiя звтАЩязку та його розвиток
Автоматика, телемеханика и связь
Анализ режимов автоматического управления