Основи теорii сигналiв

Спектральний метод аналiзу, заснований на поданнi сигналу у виглядi суми (або iнтегралу) гармонiчних складових (гармонiк) i подальшому розрахунку проходження кожноi з гармонiк через коло. Вихiдний сигнал знаходиться на основi принципу накладання у виглядi суми вiдгукiв на кожну з гармонiк вхiдного сигналу. Сукупнiсть гармонiк, на якi розкладаються сигнали, називаiться iх спектрами.

Вивчення спектрiв розпочинаiться з перiодичних iмпульсних вiдеосигналiв.

РЖмпульсними називаються струми i напруги кiнцевоi енергii, миттiвi значення яких вiдмiннi вiд нуля впродовж деякого (як правило, досить невеликого) iнтервалу часу.

Перiодичнi послiдовностi iмпульсiв (рис. 1) вiдносяться до перiодичних несинусоiдних процесiв i знаходять широке використання в радiоелектронiцi.

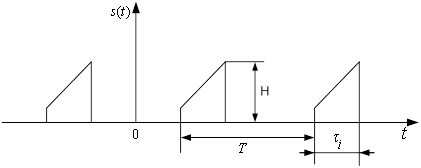
Рисунок 1 тАУ Перiодична послiдовнiсть iмпульсiв

Перiодичнi послiдовностi iмпульсiв характеризуються iх формою, тривалiстю , перiодом повторення Ва(або частотою ), висотою (максимальним значенням) тАУ.

Тривалiсть iмпульсiв Вазнаходять на деякому рiвнi вiд висоти Ва(у границi на нульовому рiвнi), або як iнтервал часу, в якому мiститься визначена потужнiсть iмпульсу (зазвичай 90або бiльше).

РЖнколи вводиться також вторинний параметр тАУ щiлиннiсть:

Перiодична послiдовнiсть iмпульсiв, описуiться функцiiю, яка задовольняi умови Дiрiхле i може бути подана нескiнченим рядом (рядом ФуртАЩi) гармонiк з частотами, кратними частотам слiдування , :

, (1)

де ВатАУ комплексна амплiтуда -i гармонiки,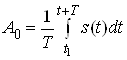 тАУ постiйна складова iмпульсiв (середнi значення).

Сукупнiсть амплiтуд гармонiк Ваназивають спектром амплiтуд або амплiтудно-частотним спектром (АЧС).

Сукупнiсть початкових фаз Ваназивають спектром фаз або фазочастотним спектром (ФЧС).

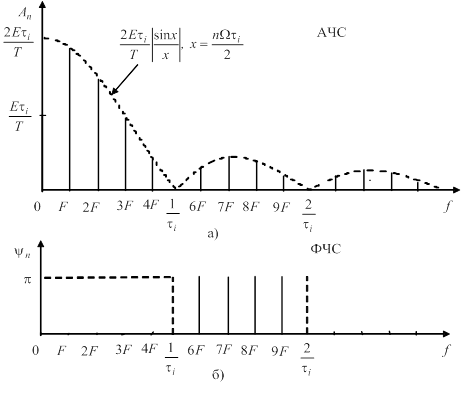
АЧС i ФЧС зображують у виглядi графiкiв, в яких за вiссю абсцис вiдкладають частоту ( або ), а за вiссю ординат тАУ амплiтуди гармонiк у АЧС i початковi фази у ФЧС (рис. 2). Властивiстю спектра перiодичного коливання i поступове зменшення амплiтуд гармонiк зi зростанням iх частоти. Це дозволяi оперувати з нескiнченними межами сум у (1), а з сумами обмеженими . 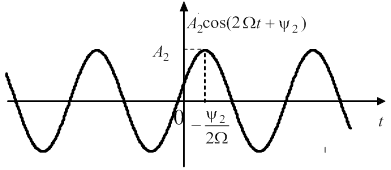Кожнiй парi ординат графiкiв АЧС i ФЧС вiдповiдна частота однiii з гармонiк, тобто ,, повнiстю визначають параметри цiii гармонiки. Наприклад, на рис. 3 побудована у функцii часу друга гармонiка спектра з частотою , амплiтудою Ваi зсувом максимуму косинусоiди вправо (вiдносно ) на вiдрiзок часу пропорцiйний .

Оскiльки середня потужнiсть перiодичного сигналу i сумою потужностей гармонiчних складових сигналу i потужностi сталоi складовоi, ширина спектра визначаiться частотою коливання з амплiтудою , яка ще впливаi на значення середньоi потужностi на заданому рiвнi:

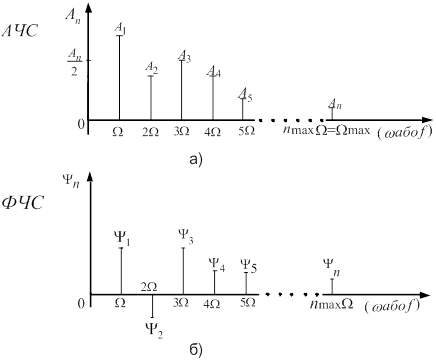
Рисунок 2 тАУ Графiки АЧС (а) i ФЧС (б)

У тих випадках, коли ВатАУ парна функцiя часу, Вав (1) дорiвнюi нулю або . Для непарноi функцii, навпаки, ряд ФуртАЩi складаiться тiльки iз синусоiдних коливань, тобто Вадорiвнюi Ваабо .

У двох послiдовностях iмпульсiв Ваi , якi вiдрiзняються тiльки початком вiдлiку часу, АЧС однаковi, а вiдрiзняються тiльки iх ФЧС. Дiйсно, якщо , тодi

Ва(2)

Таким чином, при зсувi сигналу на Вафази його гармонiки змiнюiться на .

Як iлюстрацii наведемо результати розкладу в ряд ФуртАЩi перiодичноi послiдовностi прямокутних iмпульсiв (рис. 4), яку аналiтично можна записати у виглядi:

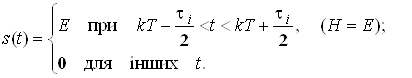
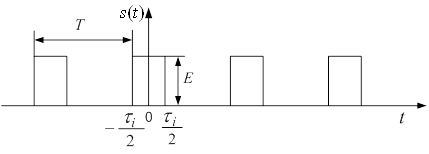
Рисунок 4 тАУ Перiодична послiдовнiсть прямокутних iмпульсiв

На пiдставi (2) Ваможна подати у виглядi:

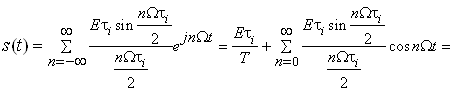
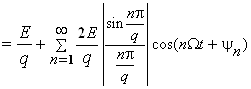. (3)

Обвiдна амплiтуд спектра визначаiться значеннями функцii:

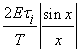де 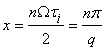, при , тобто , Ваi амплiтуди гармонiк дорiвнюють нулю.

Позитивним значенням Вавiдповiдають нульовi значення фаз гармонiк, вiдтАЩiмним тАУ початковi фази рiвнi , тому що , тобто початковi фази гармонiк у (3) визначаються як:

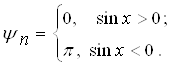
Графiки АЧС i ФЧС наведено на рис. 5 Графiки побудовано для щiльностi . Такi спектри мають назву дискретних.

При змiнюваннi тривалостi iмпульсiв або частоти iх повторення змiнюються i спектри. Рис. 6 iлюструi змiни у спектрах при збiльшеннi тривалостi iмпульсiв Ваi незмiннiй частотi повторення . При збiльшеннi тривалостi iмпульсiв вiдбуваiться ВлстисненняВ» спектра тАУ гармонiчнi складовi, якi мають найбiльшi амплiтуди, зсуваються в область бiльш низьких частот. РЖнтервали мiж спектральними лiнiями за частотою не змiнюються.

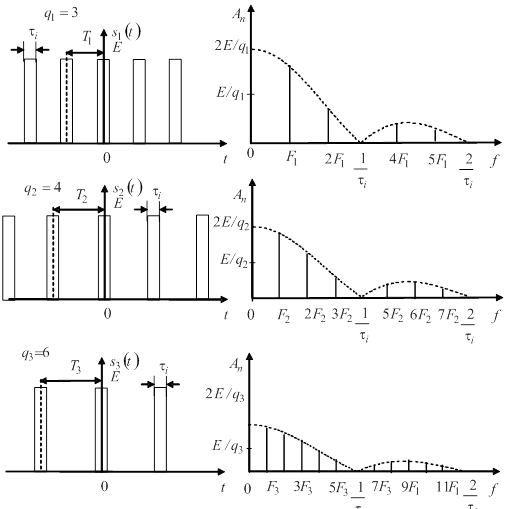
Рис. 7 iлюструi змiни у спектрах при збiльшеннi перiоду i незмiннiй тривалостi iмпульсу. Збiльшення перiоду (зменшення частоти слiдування) призводить до зменшення iнтервалу мiж спектральними лiнiями. При цьому зменшуiться i амплiтуда всiх складових спектра, що фiзично пояснюiться зменшенням потужностi у перiодичноi послiдовностi iмпульсiв.

Якщо спрямувати перiод до нескiнченностi, амплiтуди зменшаться до нескiнченно малих величин, а спектральнi лiнii наблизяться одна до одноi, тобто спектр стане суцiльним. Вiдбудеться перехiд вiд перiодичноi послiдовностi до одиночного iмпульсу.

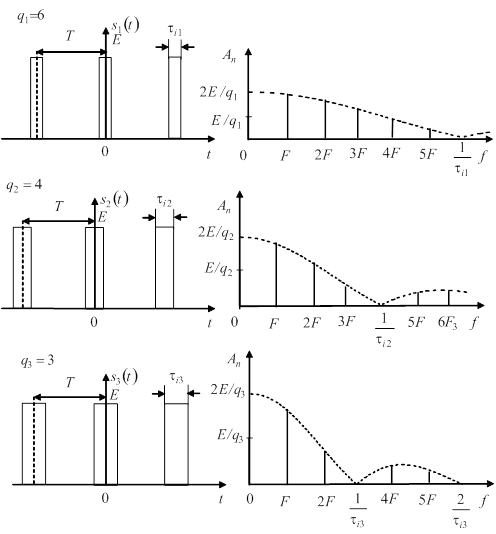
Рисунок 6 тАУ Вплив тривалостi iмпульсiв на АЧС

Якщо початок вiдлiку часу не збiгаiться з серединою iмпульсiв (рис. 8,а), вiдповiдно до формули (3) змiнюiться тiльки ФЧС, як показано на рис. 8,б.

Спектри неперiодичних одиночних сигналiв оцiнюiться, так званою, спектральною густиною , у вiдповiдностi з перетворенням ФуртАЩi:

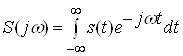Модуль спектральноi густини маi розмiрнiсть В/Гц або А/Гц в залежностi вiд розмiрностi сигналу (В або А).

Вiдновлення одиночного сигналу за його спектральною густиною виконуiться за допомогою оберненого перетворення ФуртАЩi:

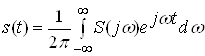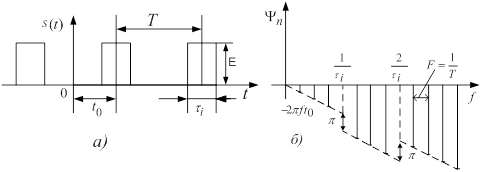
Рисунок 8 тАУ Вплив початку вiдлiку часу на ФЧС

Спектральна густина одиночного прямокутного iмпульсу висотою Ваi тривалiстю Ваописуiться виразом:

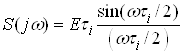Частотна залежнiсть модуля спектральноi густини Ва(АЧС) i частотна залежнiсть аргументу спектральноi густини Ва(ФЧС) одиночного прямокутного iмпульсу наведенi на рис. 9.

Для розрахунку вiдгук кiл спектральним методом використовують комплексний коефiцiiнт передачi кола , який дозволяi визначити вихiднi сигнали у випадках:

а) перiодичного сигналу тАУ

перiодичний послiдовнiсть iмпульс спектр амплiтуда

де , ,тАУ комплексна амплiтуда, амплiтуда i початкова фаза -i гармонiки вхiдного сигналу вiдповiдно; , , ВатАУ комплексний коефiцiiнт передачi, значення АЧХ i ФЧХ кола для частоти -i гармонiки вхiдного сигналу вiдповiдно;

б) неперiодичного сигналу тАУ

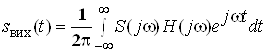де ВатАУ спектральна густина вхiдного сигналу.

Розглянутi вище сигнали мають спектри в областi низьких частот i такi сигнали називають вiдеосигналами. На вiдмiну вiд них, радiосигнали з амплiтудною, частотною або фазовою модуляцiiю мають спектри, сконцентрованi поблизу носiйноi частоти .

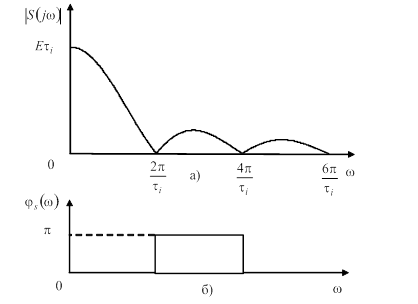
Рисунок 9 тАУ АЧС (а) i ФЧС (б) одиночного прямокутного iмпульсу наведеного на рис. 8,а

Якщо у носiйного коливання , амплiтуда змiнюiться за законом Вавiдносно деякого середнього рiвня , формуiться амплiтудно-модульоване коливання (АМК), яке можна записати у виглядi:

де постiйний коефiцiiнт Вавибраний таким, щоб амплiтуда коливань була завжди додатною.

Якщо модулююче коливання Вамiстить декiлька гармонiчних складових, якi поданi рядом:

, (4)

тодi модульоване коливання набуваi вигляду:

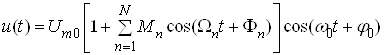, (5)

де величини ВатАУ парцiальнi (частковi) коефiцiiнти модуляцii, .

Подамо модулюючий сигнал (4) в iншому виглядi, пронормувавши амплiтуди гармонiк за амплiтудою першоi гармонiки.

де 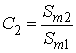; 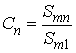ВатАУ нормованi амплiтуди гармонiк.

Тодi у виразi (5) парцiальний коефiцiiнт модуляцii -i гармонiки можна подати як:

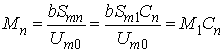Спектр АМК (1) пiсля тригонометричних перетворень набуваi вигляду

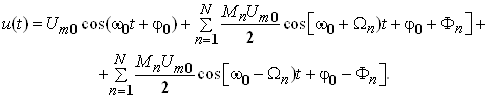Ва(6)

Якщо АЧС модулюючого коливання маi вигляд, наведений на рис. 2, а), тодi у вiдповiдностi до (2) матимемо спектр АМК, представлений на рис. 10.

Рисунок 10 тАУ АЧС амплiтудно-модульованого коливання

Таким чином, спектр АМК можна подати як перенесений на носiйну частоту спектр модулюючого вiдеосигналу. Спектр мiстить носiйне коливання i двi боковi смуги частот тАУ ВлнижнюВ» з частотами Ваi ВлверхнюВ» з частотами . Рiвень бокових частот визначаiться вiдповiдними коефiцiiнтами глибини модуляцii , а ширина спектра дорiвнюi . Такий спектр вiдповiдаi радiосигналу.

Частковим випадком АМК i балансна модуляцiя або амплiтудна манiпуляцiя, коли радiосигнал отримуiмо у виглядi:

При цьому у випадку модулюючого сигналу Ваз дискретним спектром (4) спектр радiосигналу (2) вiдрiзнятиметься вiдсутнiстю носiйного коливання.

У випадку, коли балансна модуляцiя здiйснюiться неперiодичним сигналом, спектральна густина радiосигналу маi вид:

де тАУ спектральна густина модулюючого вiдеосигналу.

Наприклад, спектральна густина радiосигналу на разi модулюючого коливання у виглядi одиночного прямокутного радiоiмпульсу за умов балансноi модуляцii описуiться виразом:

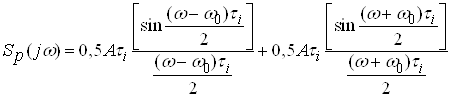Таким чином, амплiтудна манiпуляцiя одиночним сигналом призводить до переносу спектра модульованого сигналу в область частот .

Наявнiсть вiдтАЩiмних частот при спектральному аналiзi пояснюiться комплексною формою запису ряду ФуртАЩi, або iнтеграла ФуртАЩi, в яких дiйсна змiнна часу коливання Ваформуiться за допомогою векторiв, що обертаються як у додатному напрямi з частотою , так i у вiдтАЩiмному з частотою .

Вместе с этим смотрят:

GPS-навигация

IP-телефония. Особенности цифровой офисной связи

РЖсторiя звтАЩязку та його розвиток

Автоматика, телемеханика и связь

Анализ режимов автоматического управления