Розрахунки надiйностi електронноi апаратури
РОЗРАХУНКИ НАДРЖЙНОСТРЖ ЕЛЕКТРОННОРЗ АПАРАТУРИ (ЕА)
1. Аналiтичний метод розрахунку надiйностi
Пiд розрахунком надiйностi розумiтимемо визначення числових значень показникiв за будь-якими вихiдними даними. У звтАЩязку iз включенням кiлькiсних показникiв надiйностi у технiчнi вимоги на апаратуру виникла необхiднiсть не тiльки теоретичноi, а й практичноi перевiрки виконання цих вимог за статистичними даними. Вирiшення цiii задачi потребуi розробки визначених математичних методiв, а також проведення ряду органiзацiйних заходiв по збиранню статистичних даних у процесi експлуатацii.
Розрiзняють аналiтичнi методи розрахункiв при проектуваннi апаратури i розрахунки надiйностi за статистичними даними, отриманими у процесi експлуатацii або випробовування.
Загальнi вимоги до надiйностi ЕА встановлюються з урахуванням призначення, умов експлуатацii та наслiдкiв вiдмов апаратури. Пiд час розробки завдання на проектування у технiчне завдання (ТЗ) зазвичай включають такi питання:
- перелiк показникiв надiйностi;
- кiлькiснi значення показникiв надiйностi;
- термiни розрахункiв показникiв надiйностi на етапi проектування;
- методика, умови та мiсце випробовувань апаратури на надiйнiсть;
- точнiсть оцiнки результатiв випробовувань на надiйнiсть.
Складна радiоелектронна апаратура, в тому числi й побутова, складаiться з окремих блокiв, модулiв, елементiв, вiд надiйностi яких залежить реалiзацiя встановлених параметрiв надiйностi РЕА в цiлому. Отже, необхiдно розподiлити вимоги до надiйностi окремих частин апаратури, виходячи з загальних вимог до надiйностi РЕА в цiлому.
Ймовiрнiсть безвiдмовноi роботи системи за час t:
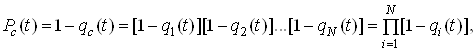 Ва(1)
Ва(1)
де qc тАУ ймовiрнiсть вiдмови системи (апаратури);
qi тАУ ймовiрнiсть вiдмови модуля (блока);
N тАУ кiлькiсть модулiв (блокiв).
Пiд час розгляду методiв розрахунку надiйностi вважатимемо, що нiяких попереднiх заходiв з ii пiдвищення не вжито, елементи, якi використовуються, типовi i зтАЩiднанi мiж собою послiдовно.
Залежнiсть мiж ймовiрнiстю безвiдмовноi роботи елемента та iнтенсивнiстю його вiдмов при розподiлi часу безвiдмовноi роботи за довiльним законом визначаiться виразом:
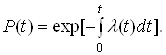 (2)
(2)
Ймовiрнiсть безвiдмовноi роботи апаратури з послiдовним зтАЩiднанням елементiв за надiйнiстю можна показати у виглядi добутку ймовiрностей безвiдмовноi роботи ii елементiв:
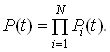 Ва(3)
Ва(3)
Замiнивши Pi(t) його значенням з попереднього рiвняння, запишемо:
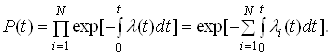 Ва(4)
Ва(4)
Позначивши:
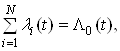
отримаiмо:
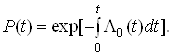 Ва(5)
Ва(5)
Як правило, будь-яка апаратура складаiться з великоi кiлькостi груп рiзних елементiв, якi мають приблизно однакову надiйнiсть. Тодi для апаратури, яка маi k груп елементiв, отримаiмо iнтенсивнiсть вiдмов:
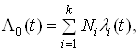
де Ni тАУ кiлькiсть елементiв у групi.
Пiдставивши отриманий вираз у формулу (5), маiмо:
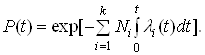 Ва(6)
Ва(6)
В окремому випадку, коли iнтенсивнiсть вiдмов можна вважати постiйною в часi, тобто для експоненцiального закону:
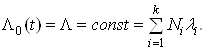
![]() Ва(7)
Ва(7)
Таким чином, ми отримали формулу ймовiрностi безвiдмовноi роботи апаратури при експоненцiальному законi розподiлу iнтенсивностi вiдмов.
Важливою властивiстю експоненцiального закону i те, що ймовiрнiсть безвiдмовноi роботи протягом заданого промiжку часу t не залежить вiд того, скiльки часу прилад працював до того.
Середнiй час роботи до першоi вiдмови (або напрацювання на вiдмову), показники ремонтопридатностi та готовностi ми розглядали у попереднiх лекцiях.
При розрахунках показникiв ремонтопридатностi i готовностi середня тривалiсть поточного ремонту зазвичай береться з досвiду експлуатацii ранiше створених аналогiчних радiоелектронних засобiв.
Таким чином, для аналiтичного розрахунку надiйностi необхiдно розподiлити вимоги за надiйнiстю окремих вузлiв, блокiв, виходячи iз загальних вимог до надiйностi пристрою в цiлому; мати данi про iнтенсивностi вiдмов елементiв, закон розподiлу вiдмов та середнiй час поточного ремонту.
2. Розрахунки надiйностi за статистичними даними
Для оцiнки надiйностi за статистичними даними необхiдна велика робота щодо правильного та обтАЩiктивного збирання цих даних. Обсяг iнформацii, яка маi бути зiбрана, визначаiться метою оцiнки, особливостями апаратури та умовами ii експлуатацii. Для визначення кiлькiсних показникiв надiйностi та виявлення найбiльш надiйних елементiв пiд час збирання статистичних даних необхiдно отримати:
- вiдомостi про блок, вузол, елемент, якi вiдмовили, та iх виробникiв;
- вiдомостi про час настання вiдмови;
- вiдомостi про причину вiдмови;
- вiдомостi про iнтенсивнiсть вiдмов окремих елементiв, блокiв апаратури в цiлому;
- вiдомостi про час ремонту на мiсцi, у майстернi; час простою.
При розрахунку надiйностi за статистичними даними для кожного типу апаратури складаiться таблиця потоку вiдмов. За результатами цiii таблицi будуiться варiацiйний ряд напрацювання даного пристрою. При великiй кiлькостi спостережень (декiлька сотень) варiацiйний ряд перестаi бути зручною формою запису статистичного матерiалу. Для додання йому бiльшоi компактностi i наочностi ряд пiддаiться додатковiй обробцi.
Для цього весь дiапазон зафiксованих значень вiдмов розподiляiться на iнтервали часу Δti i пiдраховуiться кiлькiсть вiдмов ni, якi припадають на кожен i - й iнтервал. Отримали статистичний ряд.
За даними статистичного ряду будуються гiстограми для оцiнки показникiв надiйностi. На рис. 1 як приклад наведена гiстограма ймовiрностi безвiдмовноi роботи апаратури P(t):
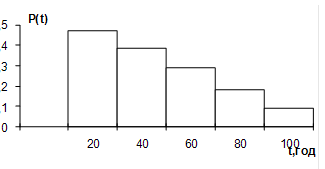
Рисунок 1 тАУ Гiстограма ймовiрностi безвiдмовноi роботи апаратури
У подальшому побудованi гiстограми апроксимуються кривою, за виглядом якоi можна орiiнтовно встановити закон розподiлу вiдмов шляхом порiвняння з вiдповiдними теоретичними кривими. Основною особливiстю оцiнки надiйностi за статистичними даними i обмеженiсть статистичного матерiалу, якого недостатньо для точного визначення експлуатацiйних показникiв.
Слiд пiдкреслити, що будь-яке значення шуканого показника, обчисленого на основi обмеженоi кiлькостi дослiдiв, завжди мiститиме елементи випадковостi. Таке наближене, випадкове значення показника називають оцiнкою показника.
Позначимо оцiнку параметра символом ![]() . Щодо оцiнки
. Щодо оцiнки ![]() Вапараметра v, висуваiться ряд вимог, яким вона маi задовольняти.
Вапараметра v, висуваiться ряд вимог, яким вона маi задовольняти.
По-перше, оцiнка ![]() Вапри збiльшеннi кiлькостi дослiдiв п маi наближатися до параметра v. Оцiнка, що маi такi властивостi, називаiться обТСрунтованою.
Вапри збiльшеннi кiлькостi дослiдiв п маi наближатися до параметра v. Оцiнка, що маi такi властивостi, називаiться обТСрунтованою.
По-друге, бажано, щоб оцiнка ![]() Ване мала систематичноi помилки, тобто, щоб була виконана умова:
Ване мала систематичноi помилки, тобто, щоб була виконана умова:
![]()
Оцiнка, яка задовольняi наведенiй умовi, при якiй ii математичне сподiвання дорiвнюi параметру, який вона оцiнюi, називаiться незсуненою.
По-третi, вибрана незсунена оцiнка повинна мати порiвняно з iншими оцiнками найменшу дисперсiю, тобто:
![]()
Оцiнка, яка маi такi властивостi, називаiться ефективною. На практицi часто потрiбно не тiльки знайти статистичне математичне сподiвання ![]() Ваi дисперсiю
Ваi дисперсiю ![]() для параметра v, а й оцiнити iх точнiсть та надiйнiсть. Потрiбно знати, до яких помилок може призвести замiна параметра v його точковою оцiнкою
для параметра v, а й оцiнити iх точнiсть та надiйнiсть. Потрiбно знати, до яких помилок може призвести замiна параметра v його точковою оцiнкою ![]() Ваi з якою мiрою впевненостi можна очiкувати, що цi помилки не вийдуть за певну межу.
Ваi з якою мiрою впевненостi можна очiкувати, що цi помилки не вийдуть за певну межу.
Для характеристики точностi та надiйностi оцiнки ![]() Вакористуються так званим довiрчим iнтервалом i довiрчою ймовiрнiстю. Нехай для параметра v отримана з п дослiдiв незсунена оцiнка
Вакористуються так званим довiрчим iнтервалом i довiрчою ймовiрнiстю. Нехай для параметра v отримана з п дослiдiв незсунена оцiнка ![]() . Оцiнiмо ймовiрнiсть, при якiй допущена помилка не перевищить деякоi величини ε. Позначимо цю ймовiрнiсть:
. Оцiнiмо ймовiрнiсть, при якiй допущена помилка не перевищить деякоi величини ε. Позначимо цю ймовiрнiсть:
![]() Ва(8)
Ва(8)
Це i ймовiрнiсть того, що справжнi (дiйсне) значення v мiститиметься в межах ![]()
Ймовiрнiсть Р(ε) називаiться довiрчою ймовiрнiстю, межi (границi) ![]() довiрчими межами (границями), iнтервали РЖε=
довiрчими межами (границями), iнтервали РЖε=![]() В±ε тАУ довiрчими iнтервалами.
В±ε тАУ довiрчими iнтервалами.
Довiрчий iнтервал характеризуi точнiсть отриманого результату, а довiрча ймовiрнiсть тАУ його надiйнiсть.
2.1 Довiрчий iнтервал при нормальному розподiлi
Нехай величина Х розподiлена за нормальним законом з параметрами Мх i σх. Розглянемо питання про знаходження довiрчих границь для математичного сподiвання.
Потрiбно знайти ймовiрнiсть нерiвностi:
![]() (9)
(9)
Якби закон розподiлу ![]() Вабув вiдомим, то знаходження ймовiрностi нерiвностi (9) не викликало б складнощiв. Проте закон розподiлу оцiнки
Вабув вiдомим, то знаходження ймовiрностi нерiвностi (9) не викликало б складнощiв. Проте закон розподiлу оцiнки ![]() Вазалежить вiд розподiлу величини Х та ii невiдомих параметрiв Мх i σх.
Вазалежить вiд розподiлу величини Х та ii невiдомих параметрiв Мх i σх.
Нам вiдомо, що величина Х розподiлена за нормальним законом, але зважаючи на те, що параметри Мх i σх цього закону невiдомi, скористуватися цим законом розподiлу неможливо.
Щоб обiйти це ускладнення, введемо замiсть випадковоi величини ![]() Ваiншу випадкову величину Тт:
Ваiншу випадкову величину Тт:
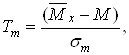 Ва(10)
Ва(10)
де 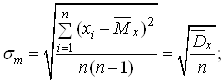 Ва(11)
Ва(11)
п тАУ кiлькiсть спостережень;
![]() ВатАУ статистична дисперсiя величини Х.
ВатАУ статистична дисперсiя величини Х.
В математичнiй статистицi доведено, що випадкова величина Тт пiдкоряiться так званому закону Стьюдента:
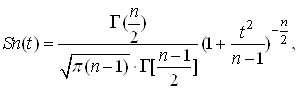 (12)
(12)
де Г(п/2) тАУ гамма тАУ функцiя;
п тАУ кiлькiсть спостережень.
З рiвняння (12) видно, що розподiл Стьюдента не залежить вiд параметрiв Мх i σх величини Х, а залежить тiльки вiд аргументу t i кiлькостi спостережень п.
Розподiл Стьюдента дозволяi знайти ймовiрнiсть нерiвностi ![]() Для цього задамося довiльним позитивним числом ta i знайдемо ймовiрнiсть влучення величини Тт на вiдрiзок (-ta, ta):
Для цього задамося довiльним позитивним числом ta i знайдемо ймовiрнiсть влучення величини Тт на вiдрiзок (-ta, ta):
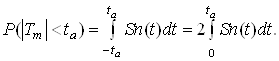 Ва(13)
Ва(13)
Пiдставимо в лiву частину цiii формули замiсть Тт його значення з формули (10) i отримаiмо:
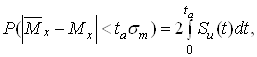 Ва(14)
Ва(14)
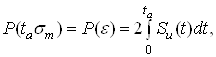 Ва(15)
Ва(15)
де ![]() тАУ довiрча ймовiрнiсть;
тАУ довiрча ймовiрнiсть;
![]()
ta тАУ квантиль розподiлу Стьюдента для вибраноi ймовiрностi P(ε) та кiлькостi ступенiв свободи r=n-1.
Функцiя ta табульована. За допомогою такоi табульованоi функцii можна вирiшувати практичнi задачi з оцiнки точностi математичного спадкування.
Довiчний iнтервал знаходиться так:
1. Задамося довiрчою ймовiрнiстю P(ε). Зазвичай P(ε)=0,9; 0,95; 0,98; 0,99.
2. Знаходимо величину σm за формулою (11).
3. Визначаiмо кiлькiсть ступенiв свободи r=n-1.
За вiдомими r та P(ε) знаходимо за таблицями [1] величину ta.
5. Помноживши ta на σm, знаходимо ε= ta∙σm тАУ половину довжини довiрчого iнтервалу.
6. Знаходимо довiрчий iнтервал ![]()
2.2 Довiрчий iнтервал при експоненцiальному розподiлi
При експоненцiальному законi розподiлу вiдмов оцiнки параметрiв λ i напрацювання до вiдмови То вiдповiдно дорiвнюють:
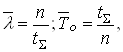 Ва(16)
Ва(16)
де tΣ тАУ сумарне напрацювання;
n тАУ кiлькiсть вiдмов в iнтервалi tΣ.
Для неремонтованих елементiв сумарне напрацювання:
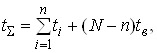 Ва(17)
Ва(17)
де ti тАУ час справноi роботи i - го елемента, який вiдмовив;
N тАУ кiлькiсть елементiв (приладiв);
tв тАУ час випробовувань;
n тАУ кiлькiсть елементiв (приладiв), що вiдмовили.
Для ремонтованих елементiв сумарне напрацювання:
![]() Ва(18)
Ва(18)
Для випадку, коли випробовування проводяться до тих пiр, поки не вiдмовлять всi елементи (прилади), якi поставили на випробовування, сумарне напрацювання:
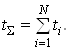 Ва(19)
Ва(19)
Довiрчий iнтервал для iнтенсивностi вiдмов λ за експоненцiальним розподiлом знаходиться з допомогою квантилiв розподiлу χ2, в яких параметрами i довiрча ймовiрнiсть та кiлькiсть ступенiв свободи r.
Нижня λн i верхня λв границi iнтенсивностi вiдмов знаходяться як:
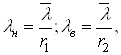 Ва(20)
Ва(20)
де ![]()
![]() . (21)
. (21)
У формулах (21) ![]() квантилi розподiлу χ2 при кiлькостi ступенiв свободи r=2n.
квантилi розподiлу χ2 при кiлькостi ступенiв свободи r=2n.
Значення коефiцiiнтiв r1 i r2 табульованi для рiзних ймовiрностей Р(ε) i кiлькостi елементiв, що вiдмовили n.
Враховуючи, що за експоненцiальним розподiлом ![]() Ваотримаiмо:
Ваотримаiмо:
![]()
![]() (22)
(22)
На практицi часто потребуiться отримати в процесi випробування iнтенсивнiсть вiдмов з помилкою, яка б не перебiльшувала задану. В цьому випадку при плануваннi випробовувань потрiбно визначити кiлькiсть вiдмов п, кiлькiсть екземплярiв апаратури N, яку поставили на випробовування, сумарне напрацювання апаратури tΣ та довжину етапу випробовувань tв.
Якщо задана гранична помилка виражена у вiдсотках i дорiвнюi ξо, то:
![]()
![]()
![]() ВаВаВаВаВа (23)
ВаВаВаВаВа (23)
Для експоненцiального розподiлу часу безвiдмовноi роботи:
![]()
Тодi, при заданiй ймовiрностi Р(![]() ) i rξ=r1 визначимо кiлькiсть вiдмов п, яку необхiдно отримати в процесi випробовувань. ОбтАЩiм вибiрки за виразом (18). Результати випробовувань вважаються позитивними, якщо:
) i rξ=r1 визначимо кiлькiсть вiдмов п, яку необхiдно отримати в процесi випробовувань. ОбтАЩiм вибiрки за виразом (18). Результати випробовувань вважаються позитивними, якщо:
![]()
![]()
![]() ВаВаВаВаВаВаВаВаВа (24)
ВаВаВаВаВаВаВаВаВа (24)
2.3 Довiрчий iнтервал при розподiлi Пуассона
надiйнiсть електроапаратура експоненцiальний
Довiрчi границi у випадку розподiлу Пуассона обчислюiться за формулами :
![]() ;
;![]() Ва(25)
Ва(25)
де а тАУ параметр розподiлу Пуассона (математичне сподiвання кiлькостi вiдмов); а = λt;
n тАУ кiлькiсть вiдмов, якi виникли в процесi випробовування;
коефiцiiнти r1 i r2 визначаються за формулою (21).
Довiрчий iнтервал для iнтенсивностi вiдмов при розподiлi Пуассона знаходиться так:
1. Задаiмося довiрчою ймовiрнiстю Р(ε).
2. За заданими значеннями п та Р(ε) знаходимо коефiцiiнти r1 i r2.
3. Розраховуiмо за формулою (25) значення ан та ав параметрiв розподiлу Пуассона.
4. За заданим сумарним напрацюванням tΣ знаходимо довiрчi границi для λ:
![]()
![]()
3. Критерii згоди
Мiж статистичним розподiлом та теоретичною кривою на практицi завжди i розбiжностi. При цьому потрiбно переконатися, викликанi цi розбiжностi тiльки випадковими обставинами, якi повтАЩязанi з обмеженою кiлькiстю спостережень, або вони i iстотнi i повтАЩязанi з тим, що вибрана крива погано вирiвнюi даний статистичний розподiл. Отже, виникаi питання про узгодження теоретичного i статистичного розподiлiв. Перевiрка такоi узгодженостi здiйснюiться за критерiями згоди. Критерiями, якi найбiльш використовуються, i критерiй Колмогорова та критерiй χ2 Пiрсона.
3.1 Критерiй Колмогорова
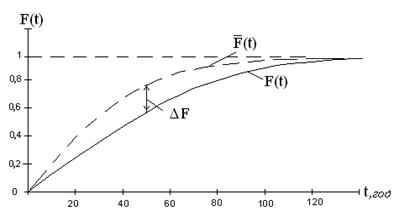
При застосуваннi критерiю згоди Колмогорова як захiд розбiжностi мiж теоретичним i статистичним розподiлом розглядаiться максимальне значення модуля рiзницi мiж теоретичною та експоненцiальною функцiями розподiлу.
На рис. 2 наведенi теоретична та експоненцiальна функцii розподiлу F(t).
![]()
Рисунок 2 тАУ Функцii розподiлу F(t)
На пiдставi цього критерiю експериментальний розподiл узгоджуiться з вибраним теоретичним, якщо виконуiться умова:
![]() , (26)
, (26)
де ![]() найбiльше вiдхилення теоретичноi кривоi вiд експоненцiальноi;
найбiльше вiдхилення теоретичноi кривоi вiд експоненцiальноi;
п тАУ загальна кiлькiсть експоненцiальних даних.
Недолiком критерiю Колмогорова i те, що вiн потребуi попереднього знання теоретичного розподiлу, тобто його можна використовувати тiльки тодi, коли вiдомi не тiльки вигляд функцii розподiлу F(t), ii параметри Мt i σt. Такий випадок дуже рiдко зустрiчаiться на практицi. Якщо все ж використовувати цей критерiй у тих випадках, коли параметри теоретичного розподiлу знаходяться за статистичними даними, то критерiй даi явно завищенi значення, що може привести до невiрних висновкiв.
3.2 Критерiй Пiрсона χ2
Критерiй χ2 Пiрсона не потребуi побудови самого закону розподiлу. Достатньо тiльки задатися загальним виглядом функцii F(t), а кiлькiснi значення параметрiв, якi входять до цiii функцii, визначаються за даними експерименту.
Припустимо, що виникло п вiдмов i, отже, маiмо ряд напрацювання То1, То2, То3, тАж Топ пристрою. Потрiбно перевiрити гiпотезу про те, що статистичний розподiл напрацювання апарата узгоджуiться з якимось вiдомим законом.
Розбиваiмо вiсь часу (вiд 0 до ∞) на k iнтервалiв Δt[(0,t1), (t1, t2)тАж(tk-2, tk-1), (tk-1, ∞)]. Розраховуiмо теоретичну ймовiрнiсть Рi потрапляння в i-й iнтервал при одному дослiдi. Пiдрахуiмо кiлькiсть пi напрацювання, якi попали в i-й iнтервал.
Тодi при перевiрцi такого узгодження з використанням критерiю χ2 Пiрсона вираховуiться ймовiрнiсть:
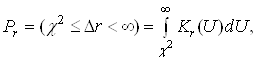 Ва(27)
Ва(27)
де ![]() ВатАУ мiра розбiжностi;
ВатАУ мiра розбiжностi;
χ2 тАУ функцiя щiльностi розподiлу, яка розраховуiться за формулою для всiх k iнтервалiв:
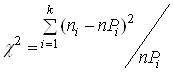 , (28)
, (28)
Де п тАУ загальна кiлькiсть вiдмов; пi тАУ кiлькiсть вiдмов в i- му iнтервалi; Рi тАУ ймовiрнiсть потрапляння вiдмов в i-й iнтервал; k тАУ кiлькiсть iнтервалiв статистичного ряду.
Функцiя розбiжностi Кr(U) запишеться як:
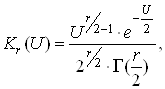 Ва(29)
Ва(29)
де ![]() кiлькiсть ступенiв свободи розподiлу.
кiлькiсть ступенiв свободи розподiлу.
Для розподiлу χ2 складенi спецiальнi таблицi, користуючись якими можна для кожного значення χ2 та кiлькостi ступенiв свободи r знайти ймовiрнiсть ![]() ВаЯкщо ймовiрнiсть
ВаЯкщо ймовiрнiсть ![]() Вато слiд вважати невдалим вибраний теоретичний розподiл. У протилежному випадку вважаiться, що вибраний теоретичний розподiл узгоджуiться з експериментальним i може бути прийнятим.
Вато слiд вважати невдалим вибраний теоретичний розподiл. У протилежному випадку вважаiться, що вибраний теоретичний розподiл узгоджуiться з експериментальним i може бути прийнятим.
Схема застосування критерiю χ2 за оцiнкою узгодження теоретичного та статистичного розподiлу:
- визначаiться χ2 за формулою (28);
- знаходиться кiлькiсть ступенiв свободи ![]()
- за знайденою величиною r та χ2 за таблицями визначаiмо ймовiрнiсть ![]() ;
;
- якщо ![]() Вагiпотеза вiдкидаiться як неправдоподiбна, при
Вагiпотеза вiдкидаiться як неправдоподiбна, при ![]() Вагiпотезу можна визнати такою, яка не суперечлива дослiдним даним.
Вагiпотезу можна визнати такою, яка не суперечлива дослiдним даним.
4. Контроль надiйностi
Контроль надiйностi маi своiю метою перевiрити гiпотезу про те, що надiйнiсть не нижче встановленого рiвня. При цьому кiнцевим результатом, як правило, i одне з двох рiшень: прийняти партiю, вважаючи надiйнiсть апаратури задовiльною, або забракувати контрольовану партiю апаратури як ненадiйну. Оскiльки контроль надiйностi проводиться на основi випробовувань визначеноi вибiрки, то пiд час прийняття рiшення можливi два види помилок:
- помилка першого роду тАУ коли добра партiя бракуiться;
- помилка другого роду тАУ коли погана партiя приймаiться.
Ймовiрнiсть помилки першого роду називаiться ризиком виробника, позначимо ii лiтерою α .
Ймовiрнiсть помилки другого роду називаiться ризиком споживача, позначимо ii лiтерою β.
РЖснують три основних методи контролю надiйностi:
- метод одноразовоi вибiрки (одинокий контроль);
- метод дворазовоi вибiрки (подвiйний контроль);
- метод послiдовного аналiзу.
Кожен з цих методiв маi своi переваги i недолiки та може бути використаний у тому або iншому конкретному випадку. Найбiльше розповсюдження в практицi контролю надiйностi отримали одинокий та метод послiдовного аналiзу. Це пояснюiться тим, що метод подвiйного контролю потребуi бiльшого часу контролю та бiльш складних розрахункiв. Цей метод ми розглядатимемо.
Найбiльш економiчним методом контролю надiйностi i послiдовний. Метод послiдовного контролю надiйностi застосовуiться на стадiях технiчного проекту або робочоi конструкторськоi документацii дослiдного зразка виробу. А тому при випробовуваннi дослiдного зразка апаратури перевага надаiться методу послiдовного аналiзу. Метод же одноразовоi вибiрки використовуiться пiд час випробовування серiйних зразкiв.
Сукупнiсть умов випробовування контрольних апаратiв i правил прийняття рiшень називаiться планом контролю.
Пiд сукупнiстю умов випробування розумiються умови бракування i приймання, заданi значення α та β, обсяг випробовувань тощо. Правила прийняття рiшень визначаються методами контролю.
4.1 Метод одноразовоi вибiрки
Метод одноразовоi вибiрки полягаi в тому, що з контрольноi партii обсягу No виробiв береться одна випадкова вибiрка обсягу N екземплярiв. Потiм виходячи з вибраних No, N, α або β, встановлюiться оцiночний норматив no. При контролi кiлькостi дефектних апаратiв партiя визначаiться надiйною, якщо кiлькiсть дефектних апаратiв ( кiлькiсть вiдмов) nk менше або дорiвнюi no, тобто:
![]() Ва(30)
Ва(30)
де no тАУ оцiночний норматив.
Якщо nk >no,то партiя вибраковуiться. Якщо контролювати середнi напрацювання на вiдмову ![]() Ва(контроль щодо напрацювання), то необхiдно так встановити сумарний час випробовувань tΣ (сумарне напрацювання виробiв на вибiрки N) та оцiночний норматив Тк, щоб забезпечувати заданi ризики α i β.
Ва(контроль щодо напрацювання), то необхiдно так встановити сумарний час випробовувань tΣ (сумарне напрацювання виробiв на вибiрки N) та оцiночний норматив Тк, щоб забезпечувати заданi ризики α i β.
Оцiночний норматив встановлюiться таким чином, що при:
![]() Ва(31)
Ва(31)
результати випробовувань оцiнюються як задовiльнi, а при:
![]() Ва(32)
Ва(32)
результати випробовувань оцiнюються як незадовiльнi (партiя бракуiться).
Тривалiсть етапу випробовувань tв при обраному обсязi вибiрки N буде:
![]() Ва(33)
Ва(33)
У подальшому розглядатимемо тiльки контроль щодо напрацювання.
Позначимо ймовiрнiсть вiдмови апаратури за час tв, за який вона визначаiться надiйною, через q1, а ймовiрнiсть вiдмови, при якiй апаратура бракуiться, через q2.
Середнi напрацювання на вiдмову надiйноi партii позначимо через То1, а ненадiйноi партii тАУ через То2. Крiм того, введемо позначення:
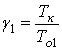 i
i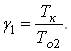 Ва(34)
Ва(34)
Для контролю надiйностi методом одноразовоi вибiрки пiд час виконання умов N≤0,1No i q1≤0,1 можна користуватися розподiлом Пуассона, тодi:
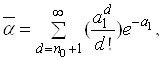 Ва(35)
Ва(35)
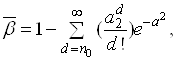 Ва(36)
Ва(36)
де ![]() ВатАУ ризик виробника, близький до заданого α;
ВатАУ ризик виробника, близький до заданого α;
![]() ризик споживача, близький до за даного β.
ризик споживача, близький до за даного β.
![]()
![]()
![]() Ва(37)
Ва(37)
Знайдемо спiввiдношення:
![]() Ва(38)
Ва(38)
Для контролю надiйностi, основаного на розподiлi Пуассон. За допомогою цих таблиць за заданими N, α, β, То1 i То2 можна визначити тривалiсть tв, значення α1 i γ1, оцiночнi нормативи no i Tk. При цьому можна визначити обсяг вибiрки N, якщо заданi α, β, q1 i q2.
В таблицях немаi значення α2 i γ2, але при α=β iх можна визначити з виразiв:
![]()
![]()
4.2 Метод послiдовного аналiзу
Послiдовний метод контролю не передбачаi попереднього обсягу вибiрки. РЖнформацiя про надiйнiсть апаратiв, якi випробовуються, накопичуiться при послiдовному, зростаючому обсязi випробовувань. Послiдовний контроль надiйностi за напрацюванням здiйснюiться у вiдповiдностi з правилами:
- партiя приймаiться, якщо сумарний час випробувань:
![]() Ва(39)
Ва(39)
- партiя бракуiться, якщо :
![]() Ва(40)
Ва(40)
- випробування продовжуються, якщо:
![]() Ва(41)
Ва(41)
де nk тАУ кiлькiсть вiдмов у робочих точках графiка послiдовного контролю напрацювання;
tk тАУ час контролю k тАУ i точки;
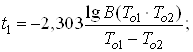 Ва(42)
Ва(42)
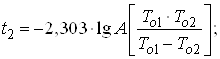 Ва(43)
Ва(43)
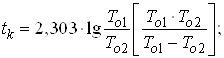 Ва(44)
Ва(44)
![]()
![]() Ва(45)
Ва(45)
To1 тАУ напрацювання на вiдмову надiйноi партii;
To2 тАУ напрацювання на вiдмову ненадiйноi партii.
Наведемо графiк контролю за методом послiдовного аналiзу (рис. 3).
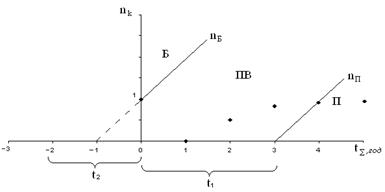
1. Зона Б тАУ приймаiться рiшення про бракування партii;
2. Зона ПВ тАУ приймаiться рiшення про продовження вимiрювання;
3. Зона П тАУ приймаiться рiшення про приймання партii.
Рисунок 3 тАУ Графiк послiдовного аналiзу
Робочими точками графiка i:
![]() Перша
Перша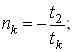
![]()
Друга![]()
![]() ВаВаВаВаВаВаВаВаВаВа (46)
ВаВаВаВаВаВаВаВаВаВа (46)
Третя![]()
![]()
Якщо α=β, то ![]() тобто ризик виробника дорiвнюi ризику споживача, то i час однаковий.
тобто ризик виробника дорiвнюi ризику споживача, то i час однаковий.
Прямi nБ i nП подiляють площину на три зони:
- зона Б тАУ приймаiться рiшення про бракування партii;
- зона ПВ тАУ приймаiться рiшення про продовження вимiрювання;
- зона П тАУ приймаiться рiшення про приймання партii.
З рiвнянь (39) i (40) видно, що прямi nБ i nП завжди паралельнi, оскiльки iх кутовi коефiцiiнти однаковi i дорiвнюють nk tk.
Для контролю за методом послiдовного аналiзу необхiдно на побудованому графiку вiдкладати дослiднi точки, отриманi у процесi випробовувань. Коли дослiднi точки мають вийти з зони продовження випробовувань (ПВ), випробовування закiнчуiться. На рис. 3 точками зображений випадок, коли випробовування закiнчились прийманням партii апаратури.
Наведемо алгоритм дii методу послiдовного аналiзу.
1. При заданих значеннях α, β, То1 i То2 знаходимо коефiцiiнти А i В.
2. За формулами (42), (43) та (44) знаходимо час напрацювання t1, t2 i tk.
3. За формулами (39) i (40) знаходимо сумарний час напрацювання апаратури.
Складемо таблицю значень nk, tΣпр i tΣбр.
Таблиця 1 тАУ Значення сумарного часу випробувань
nk | 0 | 1 | 2 | 3 | 4 | - - | k |
tΣпр | - - | ||||||
tΣбр | - - |
5. Будуiмо графiк за допомогою цiii таблицi з урахуванням формули (46).
- 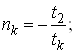
![]()
- ![]()
![]()
- ![]()
![]()
6. Ухвалюiмо рiшення про приймання або бракування партii апаратури.
5. Випробовування за оцiнкою надiйностi
Пiдвищення якостi, комфортних характеристик i функцiональних можливостей побутовоi ЕА, яка розробляiться, призводить до зростання ii складностi, отже, до збiльшення вимог щодо надiйностi апаратури. Висока надiйнiсть побутовоi ЕА i одним з основних показникiв ii якостi.
Вимоги до надiйностi побутовоi ЕА викладенi в технiчних умовах (ТУ). Нормованим показником безвiдмовностi i напрацювання на вiдмову То. Випробовуванням на надiйнiсть пiдлягають апарати дослiдноi партii, установчих серiй i серiйного виробництва. Випробовування на надiйнiсть приладiв дослiдноi партii (зразкiв) проводить пiдприiмство-розробник за участю заводу-виробника.
У табл. 2, 3 i 4 наведенi вимоги щодо безвiдмовностi рiзних видiв ПЕА згiдно з ГОСТ тАУ 21317 тАУ 87.
Таблиця 2 тАУ Вимоги щодо безвiдмовностi телевiзорiв
| Вид телевiзора | Напрацювання на вiдмову То, год | |
| Стацiонарних | Переносних | |
| Телевiзори кольорового зображення | 10200 | 8000 |
| Телевiзори чорно-бiлого зображення | 11250 | 8650 |
Таблиця 3 тАУ Вимоги щодо безвiдмовностi магнiтофонiв
| Вид магнiтофона | Напрацювання на вiдмову То, год при групi складностi | |
| 0 i 1 | 2; 3 i 4 | |
| Магнiтофони | 5000 | 4200 |
| Вiдеомагнiтофони | 5000 |
|
Таблиця 4 тАУ Вимоги щодо безвiдмовностi радiоприймачiв
| Вид радiоприймача | Напрацювання на вiдмову То, год при групi складностi | |||
| 0 | 1 | 2 | 3; 4 | |
| Стацiонарний | 11000 | 9150 | 5500 | 4500 |
| Переносний | 9150 | 9150 | 5500 | 4500 |
| Автомобiльний | 7800 | IP-телефония. Особенности цифровой офисной связи РЖсторiя звтАЩязку та його розвиток Автоматика, телемеханика и связь Анализ режимов автоматического управления | ||