Методи розвтАЩязування одновимiрних та багатовимiрних нелiнiйних оптимiзацiйних задач та задач лiнiйного цiлочислового програмування
Мiнiстерство освiти i науки Украiни
Полтавський нацiональний технiчний унiверситет iменi Юрiя Кондратюка
Факультет iнформацiйно-телекомунiкацiйних технологiй та систем
Кафедра прикладноi математики, iнформатики i математичного моделювання
КУРСОВА РОБОТА
з дисциплiни ВлМетоди оптимiзацii i дослiдження операцiйВ»
на тему: ВлМетоди розвтАЩязування одновимiрних та багатовимiрних нелiнiйних оптимiзацiйних задач та задач лiнiйного цiлочислового програмуванняВ»
301-ЕРЖ. 20 06165 КР
Керiвник роботи
кандидат фiз.-мат. Наук Радченко Г.О.
Розробила
студентка гр. 301-ЕРЖ Клюiва А.Ю.
Полтава 2009
Змiст
1. Методи розвтАЩязування одновимiрних оптимiзацiйних задач
2. Визначення найменшого значення функцii на заданому вiдрiзку за допомогою методiв одновимiрноi оптимiзацii
3. РозвтАЩязання задачi мiнiмiзацii за допомогою методу Ньютона i методу найшвидшого спуску
4. РозвтАЩязання задачi умовноi оптимiзацii за допомогою методу Франка-Вулфа i методу штрафних функцii
5. РозвтАЩязання задачi цiлочислового програмування
6. Вихiдний код програм
Список використаноi лiтератури
1. Методи розвтАЩязування одновимiрних оптимiзацiйних задач
Розглянемо детально методи розвтАЩязування одновимiрних задач, а саме: метод дихотомii, метод золотого перерiзу i метод Фiбонiччi.
Одновимiрна оптимiзацiя полягаi в знаходженнi точки 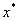 , в якiй цiльова функцiя
, в якiй цiльова функцiя 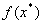 приймаi максимальне або мiнiмальне значення. Часто в постановках задач може бути заданий вiдрiзок
приймаi максимальне або мiнiмальне значення. Часто в постановках задач може бути заданий вiдрiзок 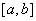 , в якому знаходиться оптимальне рiшення.
, в якому знаходиться оптимальне рiшення.
Функцiя 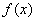 маi локальний мiнiмум в точцi
маi локальний мiнiмум в точцi 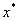 , якщо при довiльному
, якщо при довiльному 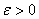 Ваiснуi окiл
Ваiснуi окiл 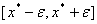 Ватакий, що для всiх значень
Ватакий, що для всiх значень 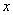 Вав цьому околi
Вав цьому околi 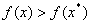 . Функцiя
. Функцiя 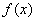 Вамаi глобальний мiнiмум в точцi
Вамаi глобальний мiнiмум в точцi 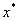 , якщо для всiх х справедлива рiвнiсть
, якщо для всiх х справедлива рiвнiсть 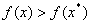 .
.
Вiдповiдно функцiя 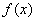 маi локальний максимум в точцi
маi локальний максимум в точцi 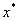 , якщо при довiльному
, якщо при довiльному 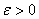 Ваiснуi окiл
Ваiснуi окiл 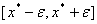 Ватакий, що для всiх значень
Ватакий, що для всiх значень 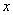 Вав цьому околi
Вав цьому околi 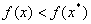 . Функцiя
. Функцiя 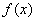 Вамаi глобальний мiнiмум в точцi
Вамаi глобальний мiнiмум в точцi 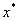 , якщо для всiх х справедлива рiвнiсть
, якщо для всiх х справедлива рiвнiсть 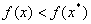 .
.
Класичний пiдхiд до задачi знаходження екстремумiв функцii полягаi в пошуку умов, яким вони повиннi задовольняти. Необхiдною умовою екстремуму в точцi 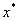 Ваявляiться рiвнiсть нулю першоi похiдноi (теорема Ферма), тобто вимагаiться розвтАЩязати рiвняння:
Ваявляiться рiвнiсть нулю першоi похiдноi (теорема Ферма), тобто вимагаiться розвтАЩязати рiвняння: 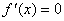 . Даному рiвнянню задовольняють як локальнi та глобальнi екстремуми, так i точки перегину функцii, тому приведена умова i лише необхiдною умовою, але не достатньою.
. Даному рiвнянню задовольняють як локальнi та глобальнi екстремуми, так i точки перегину функцii, тому приведена умова i лише необхiдною умовою, але не достатньою.
З метою отримання достатнiх умов вимагаiться обчислення значень других похiдних в точках, що задовольняють рiвняння 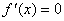 . При цьому доведено, що мiнiмуму функцii вiдповiдаi додатне значення другоi похiдноi, тобто
. При цьому доведено, що мiнiмуму функцii вiдповiдаi додатне значення другоi похiдноi, тобто 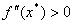 , а максимуму тАУ вiдтАЩiмне, тобто
, а максимуму тАУ вiдтАЩiмне, тобто 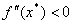 . Однак, якщо друга похiдна дорiвнюi 0, ситуацiя залишаiться невизначеною i необхiдно дослiджувати вищi похiднi. При цьому якщо перша вища похiдна не рiвна нулю маi парний порядок, то екстремум iснуi, в iншому випадку тАУ нi.
. Однак, якщо друга похiдна дорiвнюi 0, ситуацiя залишаiться невизначеною i необхiдно дослiджувати вищi похiднi. При цьому якщо перша вища похiдна не рiвна нулю маi парний порядок, то екстремум iснуi, в iншому випадку тАУ нi.
Дамо визначення унiмодальноi функцii при пошуку мiнiмуму.
Неперервна функцiя 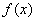 Ваназиваiться унiмодальною на вiдрiзку
Ваназиваiться унiмодальною на вiдрiзку 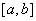 Ваякщо:
Ваякщо:
В· точка 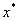 Валокального мiнiмуму функцii належить вiдрiзку
Валокального мiнiмуму функцii належить вiдрiзку 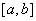 ;
;
В· для довiльних двох точок вiдрiзка х1 i х2, взятих по одну сторону вiд точки мiнiмуму, точцi х1 бiльш близькiй до точки мiнiмуму вiдповiдаi менше значення функцii, тобто при 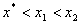 Ваабо при
Ваабо при 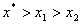 Васправедлива нерiвнiсть
Васправедлива нерiвнiсть 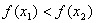 .
.
Достатня умова унiмодальностi функцii 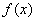 Вана вiдрiзку
Вана вiдрiзку 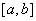 ВаТСрунтуiться на наступнiй теоремi:
ВаТСрунтуiться на наступнiй теоремi:
Якщо функцiя 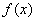 Вадвiчi диференцiйована на вiдрiзку
Вадвiчi диференцiйована на вiдрiзку 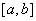 Ваi
Ваi 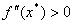 Вав будь-якiй точцi цього вiдрiзка, то
Вав будь-якiй точцi цього вiдрiзка, то 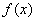 - унiмодальна функцiя на вiдрiзку
- унiмодальна функцiя на вiдрiзку 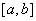 .
.
Вiдмiтимо, що умова 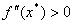 Вавизначаi множину точок, на якiй функцiя являiться опуклою вниз. Умова ж
Вавизначаi множину точок, на якiй функцiя являiться опуклою вниз. Умова ж 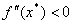 Вавизначаi опуклу вгору функцiю, яка на вiдрiзку
Вавизначаi опуклу вгору функцiю, яка на вiдрiзку 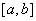 Вамаi максимум i також являiться унiмодальною.
Вамаi максимум i також являiться унiмодальною.
Метод половинного дiлення, який також називаiться методом дихотомii, являiться процедурою послiдовного пошуку мiнiмуму фунуцii. Нехай визначено вiдрiзок 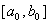 , якому належить точка локального мiнiмуму х, i функцiя
, якому належить точка локального мiнiмуму х, i функцiя 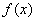 Ваявляiться унiмодальною на цьому вiдрiзку. Далi для звуження промiжку унiмодальностi використовуються двi точки
Ваявляiться унiмодальною на цьому вiдрiзку. Далi для звуження промiжку унiмодальностi використовуються двi точки  Ваi
Ваi 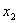 , розташованi симетрично на вiдстанi
, розташованi симетрично на вiдстанi 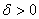 Вавiд середини вiдрiзка:
Вавiд середини вiдрiзка:
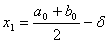 ;
;
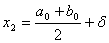 .
.
Константа  Ваповинна бути меншою допустимоi кiнцевоi довжини вiдрiзка, Δk= bk- ak> 0.
Ваповинна бути меншою допустимоi кiнцевоi довжини вiдрiзка, Δk= bk- ak> 0.
Потiм обчислюють значення функцii в цих точках y1=f(x1) i y2=f(x2) i в залежностi вiд iх спiввiдношення новi межi вiдрiзка унiмодальностi [a1, 1] будуть наступнi:
тАв y1 < y2, a1=a0 i 1=x2 ;
тАв y1 > y2, a1=x1 i 1=0 ;
тАв y1 = y2, a1=x1 i 1= x2 .
В цьому звуженому промiжку [a1, 1] знову розраховуються двi точки х1(1) iх2(1), симетричнi вiдносно його середини i значення функцii в цих точках. Процедура буде продовжуватись до тих пiр, поки не буде виконуватись умова Δk = bk-ak ≤ ε, де ε тАУ точнiсть пошуку, i тодi в якостi точки локального мiнiмуму можна наближено прийняти середину вiдрiзку 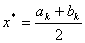 .
.
Назва методу половинного дiлення мотивована тим, що якщо величина εдостатньо мала, то довжина вiдрiзка унiмодальностi ( тАУ a) зменшуiться майже вдвiчi.
Наступним методом знаходження екстремуму для задач одновимiрноi оптимiзацii i метод золотого перерiзу.
Термiн тАЬзолотий перерiзтАЭ ввiв Леорандо да Вiнчi. Точка х1 являiться золотим перерiзом вiдрiзка 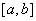 , якщо вiдношення довжини -a всього вiдрiзка до довжини -х1 бiльшоi частини дорiвнюi вiдношенню довжини бiльшоi до довжини х1-а меншоi частини, тобто х1 тАУ золотий перерiз, якщо справедлива рiвнiсть:
, якщо вiдношення довжини -a всього вiдрiзка до довжини -х1 бiльшоi частини дорiвнюi вiдношенню довжини бiльшоi до довжини х1-а меншоi частини, тобто х1 тАУ золотий перерiз, якщо справедлива рiвнiсть: 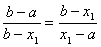 . Аналогiчно, точка х2 симетрична точцi х1 вiдносно середини вiдрiзка
. Аналогiчно, точка х2 симетрична точцi х1 вiдносно середини вiдрiзка 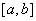 , являiться другим золотим перерiзом цього вiдрiзка.
, являiться другим золотим перерiзом цього вiдрiзка.
Вiдмiтимо властивiсть золотого перерiзу: точка х1 одночасно являiться золотим перерiзом вiдрiзка 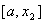 , а друга точка х2 тАУ золотим перерiзом вiдрiзка
, а друга точка х2 тАУ золотим перерiзом вiдрiзка 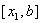 .
.
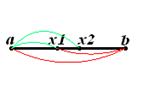
Суть методу золотого перерiзу заклечаiться в наступному. Спочатку на вихiдному вiдрiзку 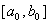 Вазнаходяться точки х1 i х2 по наступним формулам:
Вазнаходяться точки х1 i х2 по наступним формулам:
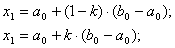
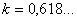 Ва- коефiцiiнт зжимання.
Ва- коефiцiiнт зжимання.
Потiм обчислюють значення функцii в точках х1 i х2, тобто 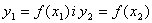 . При цьому можливi два випадки:
. При цьому можливi два випадки:
1.  , в цьому випадку новий вiдрiзок буде рiвним
, в цьому випадку новий вiдрiзок буде рiвним 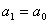 Ваi
Ваi 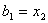 . На цьому вiдрiзку знову обираються двi точки
. На цьому вiдрiзку знову обираються двi точки 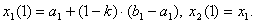
2. 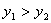 , тодi новий вiдрiзок будуть становити:
, тодi новий вiдрiзок будуть становити: 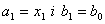 . На новому вiдрiзку також обираються двi точки
. На новому вiдрiзку також обираються двi точки 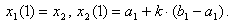
РЖ в першому i в другому випадках розраховуiться лише одна нова точка (друга вiдома). В новiй точцi обчислюiться значення функцii i знову вiдбуваiться порiвняння в двох точках, i в залежностi вiд цього обираiться новий вiдрiзок. Процедура виконуiться до тих пiр, доки не буде виконуватись умова 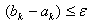 , де
, де 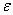 Ва- точнiсть пошуку.
Ва- точнiсть пошуку.
Розглянемо також метод Фiбоначчi для розвтАЩязування одновимiрних задач . Цей метод названий так зважаючи на появу при пошуку промiжкiв унiмрдальностi чисел Фiбоначчi i використовуiться, якщо кiлькiсть iтерацii обмежена . Суть методу в тому, що на кожному кроцi точка наступного обчислення обираiться симетрично вiдносно середини вiдрiзка локалiзацii до точки, що лежить всерединi цього вiдрiзку, уже проведеного обчислення. Тобто в процесi пошуку iнтервалу (x1; x3) з точкою х2, вже лежачою в цьому iнтервалi, наступна точка х4 завжди вибираiться так, що х3тАУх4 = х2тАУх1 або х4-х1 = х3-x2, тобто x4=х1-х2+х3.
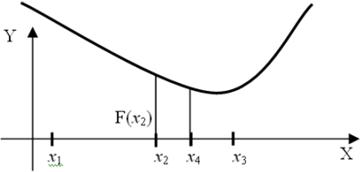
Алгоритм методу Фiбоначчi поляга в наступному:
1) задаються початковi границi вiдрiзку 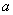 i
i 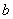 , точнiсть обчислень
, точнiсть обчислень 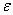 .
.
2) розраховуються початковi точки дiлення:
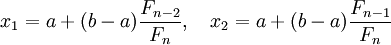
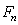 Ва- це число iз послiдовностi Фiбоначчi, яке знаходиться з умови
Ва- це число iз послiдовностi Фiбоначчi, яке знаходиться з умови 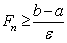 , Таким чином визначаiться також число iтерацiй . В точках
, Таким чином визначаiться також число iтерацiй . В точках 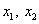 Вазнаходять значення цiльовоi функцii:
Вазнаходять значення цiльовоi функцii: 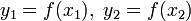 .
.
3) покладають 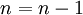 . Тодi
. Тодi
В· якщо 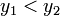 , то
, то 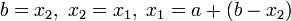 ,
, 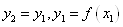 .
.
В· iнакше 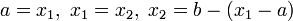 ,
, 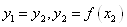 .
.
4) якщо =1, то 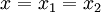 Ваi зупиняються. Значення цiльовоi функцii в цiй точцi i буде мiнiмумом функцii. РЖнакше повертаються до 3-го кроку.
Ваi зупиняються. Значення цiльовоi функцii в цiй точцi i буде мiнiмумом функцii. РЖнакше повертаються до 3-го кроку.
Вiдмiтимо, що на кожному кроцi методу Фiбоначчi точка, що лежить серединi вiдрiзку локалiзацii, дiлить його у вiдношеннi двох послiдовних чисел Фiбоначчi.
2. Визначення найменшого значення функцii на заданому вiдрiзку за допомогою методiв одновимiрноi оптимiзацii
Визначимо найменше значення функцii 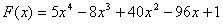 Вана вiдрiзку
Вана вiдрiзку  Ваз точнiстю
Ваз точнiстю 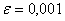 , використовуючи
, використовуючи
В· метод дихотомii:
РозiбтАЩiмо вiдрiзок  Ванавпiл i вiзьмемо двi симетричнi вiдносно центру точки
Ванавпiл i вiзьмемо двi симетричнi вiдносно центру точки 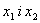 Ватакi, що
Ватакi, що  , де
, де 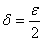 Ваi вiдкинемо ту з точок, до якоi ближче виявилась одна з двох знову поставлених точок з максимальним значенням.
Ваi вiдкинемо ту з точок, до якоi ближче виявилась одна з двох знову поставлених точок з максимальним значенням.
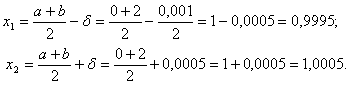
Обчислюiмо значення функцii 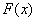 Вав цих точках:
Вав цих точках:

Оскiльки 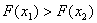 , то новi межi вiдрiзка
, то новi межi вiдрiзка 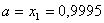 Ваi
Ваi 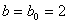 . В цьому звуженому промiжку знову розраховуiмо двi точки, симетричнi вiдносно його середини i значення функцii в цих точках. Процедура буде продовжуватись до тих пiр, поки не буде виконуватись умова
. В цьому звуженому промiжку знову розраховуiмо двi точки, симетричнi вiдносно його середини i значення функцii в цих точках. Процедура буде продовжуватись до тих пiр, поки не буде виконуватись умова 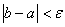 .
.
В нашому випадку 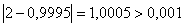 . Тому знову розраховуiмо двi точки:
. Тому знову розраховуiмо двi точки:
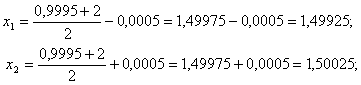
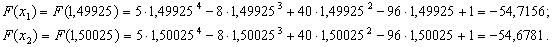
Оскiльки 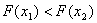 Вато новi межi вiдрiзка
Вато новi межi вiдрiзка 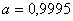 Ваi
Ваi 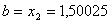 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 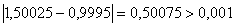 . Отже продовжуiмо процедуру.
. Отже продовжуiмо процедуру.

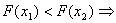 Вановi межi вiдрiзка
Вановi межi вiдрiзка 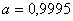 ,
, 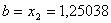 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 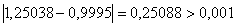 . Отже продовжуiмо процедуру.
. Отже продовжуiмо процедуру.

 Вановi межi вiдрiзка
Вановi межi вiдрiзка 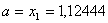 ,
, 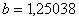 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 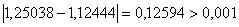 . Продовжуiмо процедуру.
. Продовжуiмо процедуру.

 Вановi межi вiдрiзка
Вановi межi вiдрiзка  ,
, 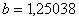 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 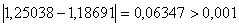 . Отже продовжуiмо процедуру.
. Отже продовжуiмо процедуру.

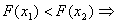 Вановi межi вiдрiзка
Вановi межi вiдрiзка 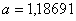 ,
, 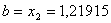 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки:  . Отже продовжуiмо процедуру.
. Отже продовжуiмо процедуру.

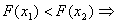 Вановi межi вiдрiзка
Вановi межi вiдрiзка 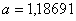 ,
, 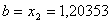 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 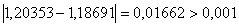 . Отже продовжуiмо процедуру.
. Отже продовжуiмо процедуру.

 Вановi межi вiдрiзка
Вановi межi вiдрiзка 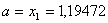 ,
, 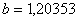 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 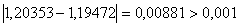 . Продовжуiмо процедуру.
. Продовжуiмо процедуру.

 Вановi межi вiдрiзка
Вановi межi вiдрiзка 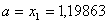 ,
, 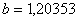 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 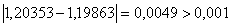 . Продовжуiмо процедуру.
. Продовжуiмо процедуру.
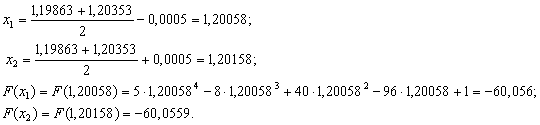
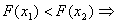 Вановi межi вiдрiзка
Вановi межi вiдрiзка 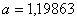 ,
, 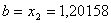 . Перевiряiмо умову зупинки:
. Перевiряiмо умову зупинки: 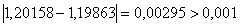 . Продовжуiмо процедуру.
. Продовжуiмо процедуру.
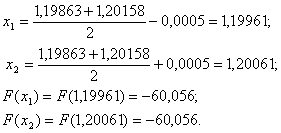
 Вановi межi вiдрiзка
Вановi межi вiдрiзка 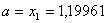 ,
, 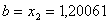 .
.
Перевiряiмо умову зупинки: 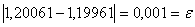 . Отже в якостi точки локального мiнiмуму можна наближено прийняти середину вiдрiзку
. Отже в якостi точки локального мiнiмуму можна наближено прийняти середину вiдрiзку 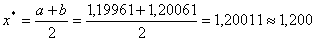 . Тодi мiнiмальне значення вихiдноi функцii буде рiвним:
. Тодi мiнiмальне значення вихiдноi функцii буде рiвним:
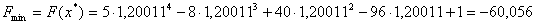 .
.
В· метод золотого перерiзу
На першiй iтерацii вiдрiзок 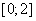 Вадiлимо двома симетричними вiдносно центра точками за формулами:
Вадiлимо двома симетричними вiдносно центра точками за формулами:
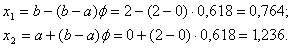
Обчислюiмо значення функцii в цих точках:
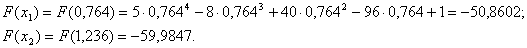
Той iз кiнцiв вiдрiзка, до якого серед знову поставлених точок ближче опинилась та, значення функцii в якiй максимальне, вiдкидаiмо. Тобто, оскiльки 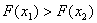 , то покладаiмо, що
, то покладаiмо, що 
 . Тепер обчислюiмо значення функцii в нових точках:
. Тепер обчислюiмо значення функцii в нових точках:
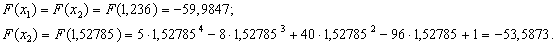
Так як i в методi дихотомii процедура буде продовжуватись до тих пiр, поки не буде виконуватись умова 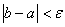 . Отже перевiримо умову зупинки:
. Отже перевiримо умову зупинки:
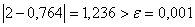 . Тому знову аналогiчно шукаiмо новi межi вiдрiзка. Оскiльки
. Тому знову аналогiчно шукаiмо новi межi вiдрiзка. Оскiльки 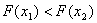 Вамаiмо:
Вамаiмо:
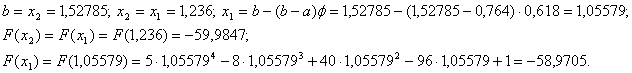 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 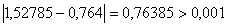 , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.

Перевiряiмо умову зупинки: 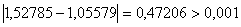 , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.

Знову перевiряiмо умову зупинки: 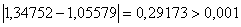 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.

Перевiряiмо умову зупинки: 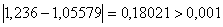 , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.
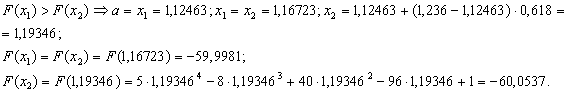
Перевiряiмо умову зупинки:  , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
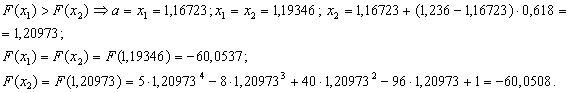
Перевiряiмо умову зупинки: 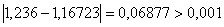 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
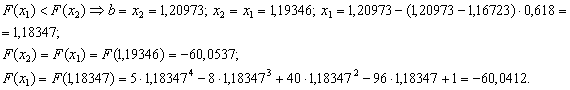 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки:  , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.
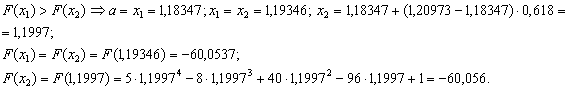 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 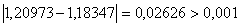 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
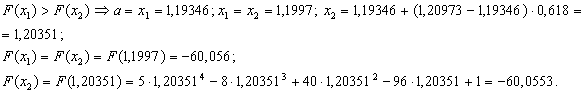 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 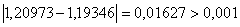 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
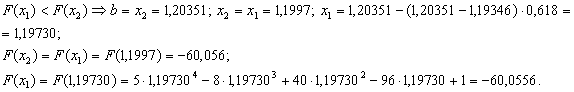 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки:  , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.
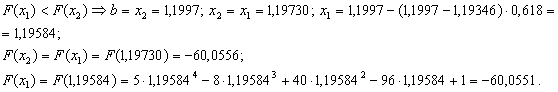 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 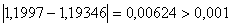 , тому продовжуiмо процедуру.
, тому продовжуiмо процедуру.
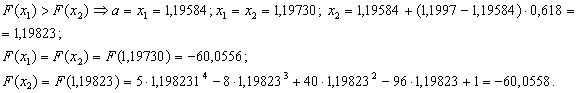 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 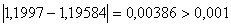 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 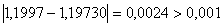 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки: 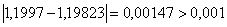 , отже продовжуiмо процедуру.
, отже продовжуiмо процедуру.
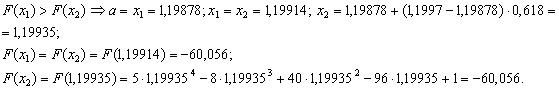 ВаПеревiряiмо умову зупинки:
ВаПеревiряiмо умову зупинки:  . Отже за точку локального мiнiмуму можна взяти середину вiдрiзку
. Отже за точку локального мiнiмуму можна взяти середину вiдрiзку 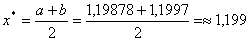 . При цьому мiнiмальне значення вихiдноi функцii буде рiвним:
. При цьому мiнiмальне значення вихiдноi функцii буде рiвним:
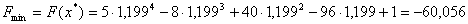 .
.
Метод дихотомii побудований таким чином, що кожний наступний iнтервал невизначеностi менше попереднього. Як бачимо, в порiвняннi з методом золотого перерiзу цей метод сходиться значно швидше (тобто через меншу кiлькiсть крокiв отримуiмо iнтервал невизначеностi заданоi довжини, що мiстить 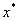 (в методi дихотомii ми зробили 11 iтерацiй, а в методi золотого перерiзу - 16). Крiм того, метод дихотомii потребуi вдвiчi менше обчислень, нiж метод золотого перерiзу. Однак мiнiмальне значення функцii знайдене обома методами спiвпадаi, тому можемо зробити висновок, що доцiльнiше використовувати метод дихотомii для зменшення затрат часу на розвтАЩязання задачi.
(в методi дихотомii ми зробили 11 iтерацiй, а в методi золотого перерiзу - 16). Крiм того, метод дихотомii потребуi вдвiчi менше обчислень, нiж метод золотого перерiзу. Однак мiнiмальне значення функцii знайдене обома методами спiвпадаi, тому можемо зробити висновок, що доцiльнiше використовувати метод дихотомii для зменшення затрат часу на розвтАЩязання задачi.
В· метод Фiбоначчi
Спочатку згенеруiмо послiдовнiсть чисел Фiбоначчi: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, тАж . Початковi обрахунки проводяться в точках: 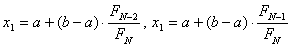 , де
, де  Ва- число Фiбоначчi, яке обираiться з умови
Ва- число Фiбоначчi, яке обираiться з умови  , тобто в нашому випадку це 18-те число Фiбоначчi:
, тобто в нашому випадку це 18-те число Фiбоначчi: 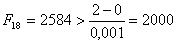 . Цi точки розташованi симетрично вiдносно середини вiдрiзку
. Цi точки розташованi симетрично вiдносно середини вiдрiзку  . На кожному кроцi точка наступного обрахунку обираiться симетрично вiдносно середини вiдрiзка локалiзацii до точки уже проведеного обрахунку, що лежить на цьому вiдрiзку. В силу властивостей чисел Фiбоначчi кiлькiсть iтерацiй строго обмежена i дорiвнюi N=18. Отже можемо знайти початковi точки дiлення:
. На кожному кроцi точка наступного обрахунку обираiться симетрично вiдносно середини вiдрiзка локалiзацii до точки уже проведеного обрахунку, що лежить на цьому вiдрiзку. В силу властивостей чисел Фiбоначчi кiлькiсть iтерацiй строго обмежена i дорiвнюi N=18. Отже можемо знайти початковi точки дiлення:
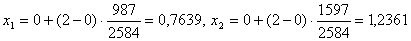 . Далi обчислюiмо значення функцii в цих точках:
. Далi обчислюiмо значення функцii в цих точках:

Оскiльки 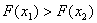 , то покладаiмо, що N=N-1=18-1=17. Новi межi вiдрiзка тепер будуть рiвними
, то покладаiмо, що N=N-1=18-1=17. Новi межi вiдрiзка тепер будуть рiвними 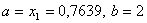 . Знаходимо новi точки дiлення:
. Знаходимо новi точки дiлення: 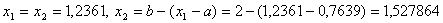 . Значення функцii в цих точках:
. Значення функцii в цих точках:
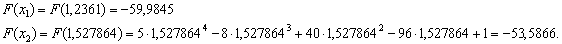
Оскiльки 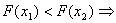 ВаN=16, новi межi вiдрiзка -
ВаN=16, новi межi вiдрiзка -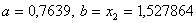 .
.

Оскiльки  ВаN=15, новi межi вiдрiзка -
ВаN=15, новi межi вiдрiзка -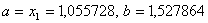 .
.
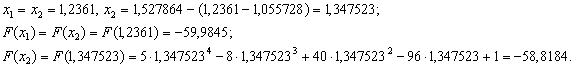
Оскiльки 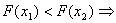 ВаN=14, новi межi вiдрiзка -
ВаN=14, новi межi вiдрiзка - .
.
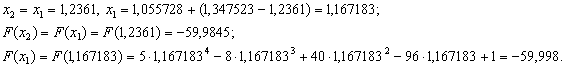
Оскiльки 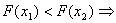 ВаN=13, новi межi вiдрiзка -
ВаN=13, новi межi вiдрiзка - .
.

Оскiльки  ВаN=12, новi межi вiдрiзка -
ВаN=12, новi межi вiдрiзка -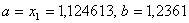 .
.
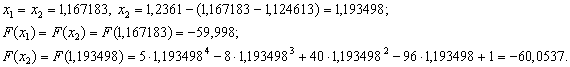
Оскiльки  ВаN=11, новi межi вiдрiзка -
ВаN=11, новi межi вiдрiзка -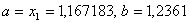 .
.

Оскiльки 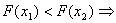 ВаN=10, новi межi вiдрiзка -
ВаN=10, новi межi вiдрiзка -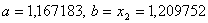 .
.
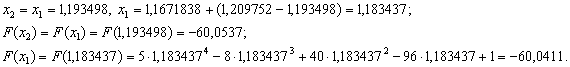
Оскiльки  ВаN=9, новi межi вiдрiзка -
ВаN=9, новi межi вiдрiзка -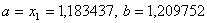 .
.
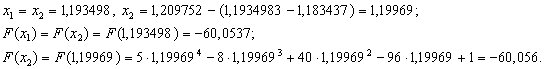
Оскiльки  ВаN=8, новi межi вiдрiзка -
ВаN=8, новi межi вiдрiзка -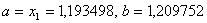 .
.
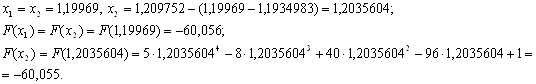
Оскiльки 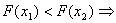 ВаN=7, новi межi вiдрiзка -
ВаN=7, новi межi вiдрiзка -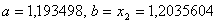 .
.

Оскiльки  ВаN=6, новi межi вiдрiзка -
ВаN=6, новi межi вiдрiзка -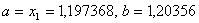 .
.
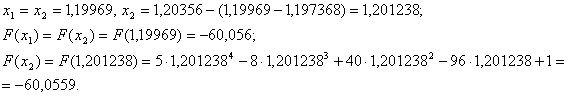
Оскiльки 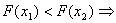 ВаN=5, новi межi вiдрiзка -
ВаN=5, новi межi вiдрiзка -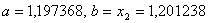 .
.
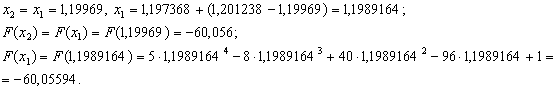
Оскiльки  ВаN=4, новi межi вiдрiзка -
ВаN=4, новi межi вiдрiзка -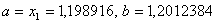 .
.

Оскiльки 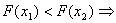 ВаN=3, новi межi вiдрiзка -
ВаN=3, новi межi вiдрiзка -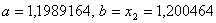 .
.
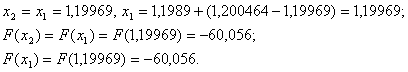
Оскiльки 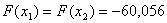 , то локальний мiнiмум досягаiться в точцi
, то локальний мiнiмум досягаiться в точцi 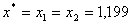 . При цьому мiнiмальне значення вихiдноi функцii буде рiвним:
. При цьому мiнiмальне значення вихiдноi функцii буде рiвним: 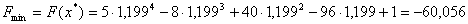 . Отже мiнiмальне значення функцii, знайдене методом дихотомii, методом золотого перерiзу i методом Фiбоначчi спiвпадають. Однак найбiльше iтерацiй було зроблено при розвтАЩзаннi задачi методом Фiбоначчi.
. Отже мiнiмальне значення функцii, знайдене методом дихотомii, методом золотого перерiзу i методом Фiбоначчi спiвпадають. Однак найбiльше iтерацiй було зроблено при розвтАЩзаннi задачi методом Фiбоначчi.
3. РозвтАЩязання задачi мiнiмiзацii за допомогою методу Ньютона i методу найшвидшого спуску
РозвтАЩяжемо задачу мiнiмiзацii для функцii  , використовуючи метод Ньютона. Це метод другого порядку, який використовуi похiдну першого i другого порядку вiд цiльовоi функцii.
, використовуючи метод Ньютона. Це метод другого порядку, який використовуi похiдну першого i другого порядку вiд цiльовоi функцii.
Перш нiж розвтАЩязувати дану задачу, зтАЩясуiмо чи маi вона точку локального мiнiмуму. Для цього побудуiмо матрицю Гессе.
Знайдемо частиннi похiднi першого i другого порядку вiд функцii 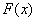 :
:
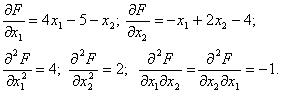
Отже матриця Гессе матиме вигляд:
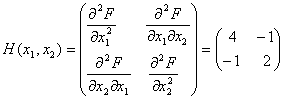 . А оскiльки головнi мiнори додатнi:
. А оскiльки головнi мiнори додатнi: 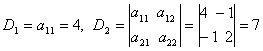 , то матриця Гессе додатно визначена. Тобто достатнi умови iснування локального мiнiмуму виконанi.
, то матриця Гессе додатно визначена. Тобто достатнi умови iснування локального мiнiмуму виконанi.
Так як цiльова функцiя i опуклою, тобто це задача опуклого програмування, а функцiя 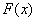 Ваi неперервно диференцiйованою в Rn , то якщо точка
Ваi неперервно диференцiйованою в Rn , то якщо точка 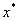 Ваi точкою локального екстремуму, то вона буде i точкою глобального екстремуму для цiii задачi.
Ваi точкою локального екстремуму, то вона буде i точкою глобального екстремуму для цiii задачi.
Отже можемо застосувати метод Ньютона. Послiдовнiсть точок, яка прямуi до точки мiнiмуму функцii 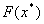 Вазгiдно цього методу знаходиться за формулою:
Вазгiдно цього методу знаходиться за формулою: 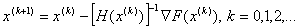 , де
, де  Ва- обернена матриця Гессе.
Ва- обернена матриця Гессе.
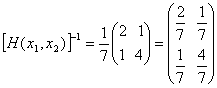 .
.
Обиремо в допустимiй областi задачi довiльну точку тАУ початкове наближення. Нехай це буде точка 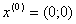 .
.
Знайдемо градiiнт цiльовоi функцii: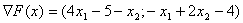 i обчислимо його в точцi
i обчислимо його в точцi 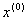 :
: 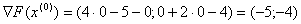 .
.
Знайдемо наступне наближення до оптимального розвтАЩязку вихiдноi задачi:  Ваi обчислимо градiiнт цiльовоi функцii в цiй точцi:
Ваi обчислимо градiiнт цiльовоi функцii в цiй точцi: 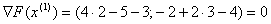 . Рiвнiсть градiiнта цiльовоi функцii нулю i необхiдною умовою iснування екстремуму функцii багатьох змiнних. Тобто оптимальний розвтАЩязок задачi
. Рiвнiсть градiiнта цiльовоi функцii нулю i необхiдною умовою iснування екстремуму функцii багатьох змiнних. Тобто оптимальний розвтАЩязок задачi  , причому
, причому 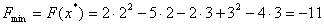 .
.
Тепер розвтАЩяжемо задачу мiнiмiзацii для функцii  , використовуючи метод найшвидшого спуску. Цей метод вiдноситься до градiiнтних методiв.
, використовуючи метод найшвидшого спуску. Цей метод вiдноситься до градiiнтних методiв.
За даним методом будуiться послiдовнiсть точок 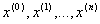 , яка прямуi до оптимального розвтАЩязку задачi -
, яка прямуi до оптимального розвтАЩязку задачi - 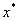 . Вiд точки
. Вiд точки 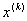 Вадо точки
Вадо точки 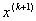 Варухаються в напрямi градiiнта цiльовоi функцii, обчисленого в точцi
Варухаються в напрямi градiiнта цiльовоi функцii, обчисленого в точцi 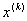 .
.
Широке застосування цього методу обумовлено тим, що в напряму антиградiiнту тАФ 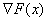 Вапохiдна функцii за напрямом досягаi найменшого значення.
Вапохiдна функцii за напрямом досягаi найменшого значення.
Алгоритм методу найшвидшого спуску:
1. Обираiмо довiльну початкову точку 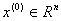 , яка називаiться початковим наближенням розвтАЩязку задачi
, яка називаiться початковим наближенням розвтАЩязку задачi 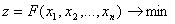 , i покладаiмо, що
, i покладаiмо, що  ВаПри цьому функцiя
ВаПри цьому функцiя  Вавважаiться опуклою i неперервно диференцiйованою в
Вавважаiться опуклою i неперервно диференцiйованою в 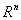 . Також обираiмо точнiсть обчислень
. Також обираiмо точнiсть обчислень 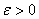 .
.
2. Обчислюiмо градiiнт цiльовоi функцii 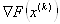 . Якщо
. Якщо  , то покладаiмо
, то покладаiмо  Ваi зупиняiмо обчислення, iнакше - переходимо до кроку 3.
Ваi зупиняiмо обчислення, iнакше - переходимо до кроку 3.
3. Шукаiмо наступне наближення за формулою: 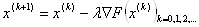 - для задачi мiнiмiзацii, а для задачi максимiзацii:
- для задачi мiнiмiзацii, а для задачi максимiзацii: 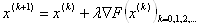 . Число
. Число 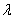 Ва- параметр, який називаiться довжиною кроку в точцi
Ва- параметр, який називаiться довжиною кроку в точцi 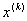 . Його обирають довiльно, однак зазвичай, параметр
. Його обирають довiльно, однак зазвичай, параметр 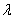 Ваобираiться з умови, щоб в точцi
Ваобираiться з умови, щоб в точцi 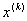 Васпостерiгалося максимальне зменшення (збiльшення) цiльовоi функцii
Васпостерiгалося максимальне зменшення (збiльшення) цiльовоi функцii 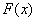 .
.
4. Перевiряiмо умову зупинки, а саме: 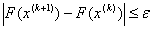 . Якщо умова виконана, то покладаiмо
. Якщо умова виконана, то покладаiмо 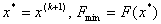 Ваi зупиняiмо обчислення, якщо нi, то переходимо до наступного кроку.
Ваi зупиняiмо обчислення, якщо нi, то переходимо до наступного кроку.
5. Покладаiмо, що 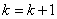 Ваi переходимо до кроку 2.
Ваi переходимо до кроку 2.
Тепер перейдемо безпосередньо до нашого прикладу.
Оберемо спочатку точнiсть обчислень 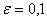 . За початкове наближення як i в методi Ньютона вiзьмемо точку
. За початкове наближення як i в методi Ньютона вiзьмемо точку 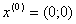 . З аналiзу, проведеного в методi Ньютона, маiмо що цiльова функцiя i опуклою i неперервно диференцiйованою в Rn, отже даний метод застосовувати можна.
. З аналiзу, проведеного в методi Ньютона, маiмо що цiльова функцiя i опуклою i неперервно диференцiйованою в Rn, отже даний метод застосовувати можна.
З методу Ньютона маiмо, що градiiнт цiльовоi функцii в точцi 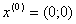 Вабуде рiвним
Вабуде рiвним 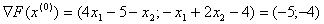 . Оскiльки
. Оскiльки  , то шукаiмо наступне наближення розвтАЩязку вихiдноi задачi:
, то шукаiмо наступне наближення розвтАЩязку вихiдноi задачi:
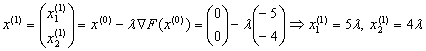 .
.
Знайдемо 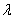 :
:  . Оскiльки
. Оскiльки 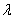 Ваобираiться з умови, щоб в точцi
Ваобираiться з умови, щоб в точцi 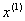 Васпостерiгалося максимальне зменшення
Васпостерiгалося максимальне зменшення 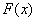 , знайдемо похiдну вiд цiльовоi функцii в точцi
, знайдемо похiдну вiд цiльовоi функцii в точцi 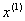 Ваi прирiвняiмо ii до нуля.
Ваi прирiвняiмо ii до нуля.
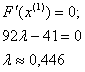
Отже можемо тепер знайти координати точки 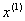 :
: 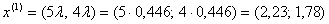 . Обчислимо значення цiльовоi функцii в цiй точцi:
. Обчислимо значення цiльовоi функцii в цiй точцi: 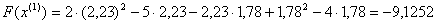 .
.
Перевiряiмо умову зупинки:
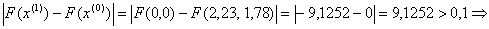 отже шукаiмо наступне наближення аналогiчним чином.
отже шукаiмо наступне наближення аналогiчним чином.
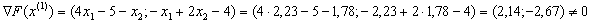
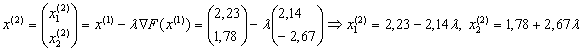
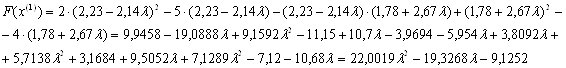
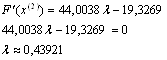
Отже можемо тепер знайти координати точки 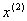 :
:  Обчислимо значення цiльовоi функцii в цiй точцi:
Обчислимо значення цiльовоi функцii в цiй точцi: 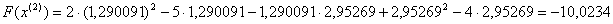 .
.
Перевiряiмо умову зупинки:
 отже шукаiмо наступне наближення:
отже шукаiмо наступне наближення:
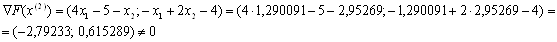


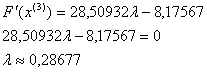
Отже можемо тепер знайти координати точки 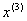 :
:  .
.
Обчислимо значення цiльовоi функцii в цiй точцi: 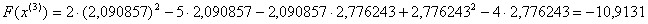 Перевiряiмо умову зупинки:
Перевiряiмо умову зупинки:
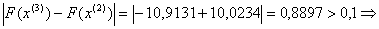 отже шукаiмо наступне наближення:
отже шукаiмо наступне наближення:
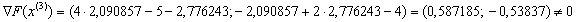
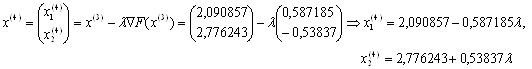

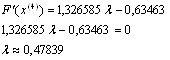
Отже можемо тепер знайти координати точки 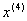 :
: 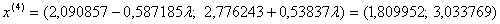 .
.
Обчислимо значення цiльовоi функцii в цiй точцi: 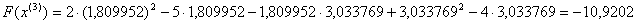 Перевiряiмо умову зупинки:
Перевiряiмо умову зупинки:
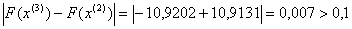 , тобто умову зупинки виконано. Отже
, тобто умову зупинки виконано. Отже 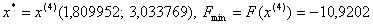 .
.
Як бачимо, розвтАЩязки задачi, знайденi обома методами майже однаковi, але при цьому метод Ньютона дав результат вже на першому кроцi ( на вiдмiну вiд методу найшвидшого спуску, де довелося робити 4 iтерацii). Це повтАЩязано з тим, що цiльова функцiя i квадратичною, а отже напрям спуску  Вазавжди спiвпадаi з напрямом в точку мiнiмуму
Вазавжди спiвпадаi з напрямом в точку мiнiмуму 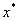 . Тобто основна перевага методу Ньютона - швидка збiжнiсть, однак при цьому суттiвим недолiком i залежнiсть збiжностi вiд початкового наближення
. Тобто основна перевага методу Ньютона - швидка збiжнiсть, однак при цьому суттiвим недолiком i залежнiсть збiжностi вiд початкового наближення 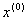 . Крiм того у випадку не квадратичноi цiльовоi функцii трудомiсткiсть iтерацii методом Ньютона може виявитись дуже великою за рахунок необхiдностi обчислення матрицi других похiдних мiнiмiзуiмоi функцii, що потребуi затрат великоi кiлькостi часу.
. Крiм того у випадку не квадратичноi цiльовоi функцii трудомiсткiсть iтерацii методом Ньютона може виявитись дуже великою за рахунок необхiдностi обчислення матрицi других похiдних мiнiмiзуiмоi функцii, що потребуi затрат великоi кiлькостi часу.
РозвтАЩязання задачi умовноi оптимiзацii за допомогою методу Франка-Вулфа i методу штрафних функцii
4. РозвтАЩяжемо задачу умовноi оптимiзацii

a. методом Франка-Вулфа
Функцiя 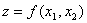 Ваявляiться вгнутою так як представляi собою суму лiнiйноi функцii (ii можна розглядати як вгнуту) i квадратичноi форми, яка являiться вiдтАЩiмно визначеною i тому також являiться вгнутою. Перевiримо завдяки матрицi Гессе вiдтАЩiмну визначенiсть функцii
Ваявляiться вгнутою так як представляi собою суму лiнiйноi функцii (ii можна розглядати як вгнуту) i квадратичноi форми, яка являiться вiдтАЩiмно визначеною i тому також являiться вгнутою. Перевiримо завдяки матрицi Гессе вiдтАЩiмну визначенiсть функцii 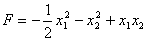 . Для цього спочатку знайдемо частиннi похiднi першого i другого порядку вiд функцii
. Для цього спочатку знайдемо частиннi похiднi першого i другого порядку вiд функцii 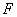 :
:
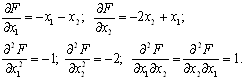
Отже матриця Гессе матиме вигляд:

Головнi мiнори :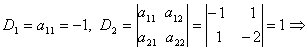 оскiльки в рядi
оскiльки в рядi 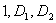 Вазнаки чергуються, то дана матриця i вiдтАЩiмно визначеною, я отже функцiя
Вазнаки чергуються, то дана матриця i вiдтАЩiмно визначеною, я отже функцiя 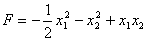 Ва- вгнута.
Ва- вгнута.
Система обмежень задачi включаi тiльки лiнiйнi нерiвностi, якi утворюють опуклу множину, отже дана задача i задачею опуклого програмування.
Задачу такого типу можна розвтАЩязувати методом Франка-Вулфа. Цей метод вiдноситься до групи градiiнтних методiв.
Розглянемо задачу:
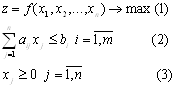
Алгоритм методу Франка-Вулфа:
1. Спочатку в допустимiй областi задачi обирають довiльну точку 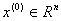 . Це можна зробити, наприклад, за допомогою методу штучного базису. Також обирають точнiсть обчислень
. Це можна зробити, наприклад, за допомогою методу штучного базису. Також обирають точнiсть обчислень 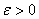 . Покладають
. Покладають 
2. Знаходять в цiй точцi градiiнт цiльовоi функцii  .
.
3. Будують функцiю 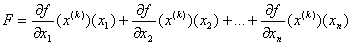 Ваi розвтАЩязують задачу максимiзацii для функцii
Ваi розвтАЩязують задачу максимiзацii для функцii 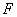 Вав областi 2-3, тобто таку задачу:
Вав областi 2-3, тобто таку задачу:
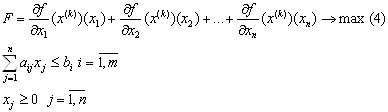
Нехай 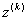 Ва- оптимальний розвтАЩязок задачi 4,2,3.
Ва- оптимальний розвтАЩязок задачi 4,2,3.
4. Шукаiмо наступне наближення за формулою:  , де
, де 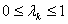 Ва- крок в точцi. Його обирають довiльно, однак краще його вибрати так, щоб
Ва- крок в точцi. Його обирають довiльно, однак краще його вибрати так, щоб 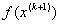 Вапри такому значеннi
Вапри такому значеннi 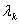 Вамала найбiльше значення. Для цього з формул 5 знаходять вираз координат вектора
Вамала найбiльше значення. Для цього з формул 5 знаходять вираз координат вектора 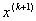 Вачерез
Вачерез 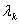 :
: 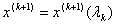 Ваi пiдставляють цей вираз у функцiю
Ваi пiдставляють цей вираз у функцiю  . Потiм розвтАЩязують систему
. Потiм розвтАЩязують систему 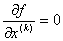 . За
. За 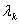 Вавибирають найменший з коренiв цього рiвняння. Якщо цей корiнь бiльше одиницi, то
Вавибирають найменший з коренiв цього рiвняння. Якщо цей корiнь бiльше одиницi, то 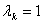 .
.
5. Перевiряють критерii зупинки: 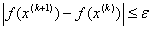 ,
,  . Якщо данi умови виконались, то покладають
. Якщо данi умови виконались, то покладають 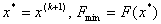 Ваi зупиняють обчислення, якщо нi, то переходимо до наступного кроку.
Ваi зупиняють обчислення, якщо нi, то переходимо до наступного кроку.
6. Покладають, що 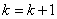 Ваi переходять до кроку 2.
Ваi переходять до кроку 2.
Тепер перейдемо безпосередньо до нашоi задачi. За початкове наближення до оптимального плану задачi обираiмо точку 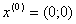 , а обчислення будемо проводити з точнiстю
, а обчислення будемо проводити з точнiстю 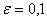 ,
, 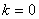 . Градiiнт цiльовоi функцii в точцi
. Градiiнт цiльовоi функцii в точцi 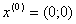
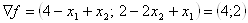 .
.
РозвтАЩяжемо за допомогою симплекс методу задачу:

оптимiзацiйний одновимiрний мiнiмiзацiя дихотомiя ньютон