Анализ эмпирического распределения

1. ТАБЛИЧНОЕ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВАРИАЦИОННОГО РЯДА

2. ХАРАКТЕРИСТИКА ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ РАСПРЕДЕЛЕНИЯ

3. ОЦЕНКА ВАРИАЦИИ ИЗУЧАЕМОГО ПРИЗНАКА

4. ХАРАКТЕРИСТИКА СТРУКТУРЫ РАСПРЕДЕЛЕНИЯ

5. ХАРАКТЕРИСТИКА ФОРМЫ РАСПРЕДЕЛЕНИЯ

6. СГЛАЖИВАНИЕ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но, по сути, ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения.

Первичные данные обрабатываются в целях получения обобщенных характеристик изучаемого явления по роду существенных признаков для дальнейшего осуществления анализа и прогнозирования; производится сводка и группировка; статистические данные оформляются с помощью рядов распределения в таблицы, в результате чего информация представляется в наглядном рационально изложенном виде, удобном для использования и дальнейшего исследования; строятся различного рода графики для наиболее наглядного восприятия и анализ информации. На основе статистических рядов распределения вычисляются основные величины статистических исследований: индексы, коэффициенты; абсолютные, относительные, средние величины и т.д., с помощью которых можно проводить прогнозирование, как конечный итог статистических исследований.

Актуальность данной темы обусловлена тем, что статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.

Основной целью написания курсовой работы является изучение методики статистического анализа рядов распределения. Для достижения поставленной цели были поставлены и выполнены следующие основные задачи:

1. Освещено понятие и виды статистических рядов распределения, и основные формы их представления.

2. Рассчитаны и проанализированы показатели, характеризующие центральную тенденцию, вариацию, структуру и форму ряда распределения.

3. Проведено сглаживание эмпирического распределения и проверены гипотезы о законе распределения.

В качестве данных для анализа в курсовой работе были использованы данные о распределении регионов Российской Федерации по количеству легковых автомобилей на 1000 чел. населения за 2005 г. (из статистического сборника ВлРегионы РоссииВ» за 2007 г.).

Методической базой для написания курсовой работы является учебное пособие Н.В. Куприенко ВлСтатистика. Методы анализа распределений. Выборочное наблюдениеВ». Также при написании работы были использованы и учебные пособия по основам статистики следующих авторов: И.И. Елисеевой, В.М. Гусарова, М.Р. Ефимовой и др.

статистический ряд распределение сглаживание

1. ТАБЛИЧНОЕ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

ВАРИАЦИОННОГО РЯДА

Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности[1]
.

Ряды распределения подразделяют:

1. Атрибутивные тАУ строятся по описательным признакам в порядке возрастания или убывания наблюденных значений признака. Примером атрибутивных рядов могут служить распределения населения по национальности, по профессиям, по полу; распределение предприятий по формам собственности.

2. Вариационные тАУ строятся по количественным признакам, например, распределение рабочих по уровню квалификации, по заработной плате, распределение студентов по успеваемости.

Вариационные ряды делятся на дискретные (в которых признак принимает только целочисленные значения) и интервальные (построены на признаках, которые могут принимать любые, в том числе и дробные значения).

Вариационные ряды распределения состоят из двух элементов: вариантов и частот. Вариантом называется числовое значение количественного признака в ряду распределения. Они могут быть положительными и отрицательными, абсолютными и относительными.

Частоты тАУ это численности отдельных вариантов или каждой группы вариационного ряда, т.е. числа, показывающие, как часто встречаются те или иные варианты в вариационном ряду. Сумма всех частот равна общему количеству элементов совокупности и называется объемом совокупности.

Частости тАУ это частоты, выраженные в виде относительных величин (в долях единицы или процентах). Сумма частостей равна единице или 100%.

Первым шагом к упорядочиванию первичного ряда данных является его ранжирование, т.е. расположение всех его данных в возрастающем или убывающем порядке.

Способы построения дискретного и интервального вариационных рядов различны, поэтому, вначале нужно определить к какому типу относится исследуемый ряд данных. Поскольку исходными данными для анализа являются данные о числе легковых автомобилей на 1000 человек населения, то вариационный ряд будет интервальным (так как значения признака могут быть дробными).

Следовательно, в первую очередь необходимо определить количество групп и интервалы группировки.

Интервал тАУ количественное значение, отделяющее одну единицу (группу) от другой, т.е. интервал очерчивает количественные границы групп[2]
.

Ориентировочно определить оптимальное количество групп с равными интервалами можно по формуле Стерджесса:

, (1.1)

где N тАУ численность единиц совокупности.

Формула Стерджесса пригодна при условии, что распределение единиц совокупности по данному признаку приближается к нормальному и при этом применяются равные интервалы в группах.

Численность единиц совокупности равна 80, следовательно по формуле Стерджесса количество групп вариационного ряда будет равно:

Однако поскольку формула Стерджесса дает приемлемые результаты только при анализе больших совокупностей, рассмотрим несколько различных вариантов распределения с различным количеством интервалов.

Ниже приведены таблицы вариационного ряда, построенные с использованием разного количества интервалов (рис. 1.1.).

Выбирая окончательный вариант табличного представления вариационного ряда из представленных вариантов, остановимся на первом тАУ n=8. При n=13 наблюдает много малонаполненных групп и нулевой интервал, при n=10 также имеются малонаполненные группы.

В таблицах первая непоименованная графа (From To) содержит интервалы значений признака ВлКоличество легковых автомобилей на 1000 чел. населенияВ».

Второй столбец ВлCountВ» тАУ абсолютные частоты (f_i), т.е. число единиц совокупности, обладающих указанным значением признака.

Cumulative Count тАУ накопленные абсолютные частоты, получаемые последовательным суммированием частот по группам. Сумма накопленных частот по каждой строке означает, какое количество единиц совокупности (регионов) имеет значение признака, не превышающее значения верхней границы данного интервала. Общая сумма накопленных частот соответствует объему изучаемой совокупности (80).

Percent тАУ частости (относительные частоты, w_i; выражаются в процентах), рассчитываются:

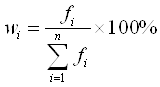, (1.2)

где:f_i тАУ число единиц i-той группы; ВатАУ общее число единиц в совокупности; w_i тАУ доля каждой группы в общем объеме совокупности.

а)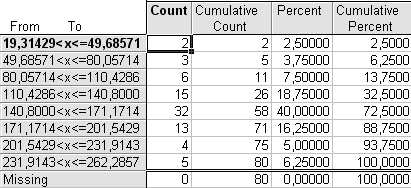

б)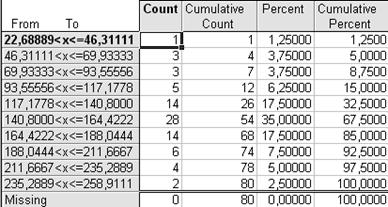

в)

Рис. 1.1. Распределение регионов России по значению показателей ВлКоличество легковых автомобилей на 1000 человек населенияВ» в 2005 г. с числом интервалов а) n=8, б) n=10, в) n=13

Cumulative percent тАУ накопленные частости тАУ это результат последовательного суммирования относительных частот по группам, итоговая сумма, очевидно, равна 100%.

Табличное представление вариационного ряда позволяет получить подробную информацию о составе и структуре изучаемой совокупности, т.е. определить какое количество единиц изучаемой совокупности обладает тем или иным значением признака и какова доля этой группы единиц в общем объеме совокупности, а также выявить закономерность изменения частот.

Из таблицы видно, что наибольшую частоту (32 или 40,0% от всего объема совокупности) имеет интервал 140,8-171,2 автомобилей на 1000 чел. населения.

Наименьшую частоту (2 или 2,5%) имеет первый интервал тАУ 19,3-49,69 автомобиля на 1000 чел. населения.

Для более наглядного представления вариационного ряда используют статистические графики.

Статистический график представляет собой чертеж, на котором при помощи условных геометрических фигур (линий, точек или других символических знаков) изображаются статистические данные. В результате этого достигается наглядная характеристика изучаемой статистической совокупности.

Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой[3]
.

Традиционно для изображения вариационных рядов распределения в отечественной практике используются графики: гистограмма, полигон, кумулята.

На рис. 1.2 представлен полигон распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г. в абсолютных частотах при количестве интервалов n=8. Он показывает, что наибольшую частоту имеет интервал 140,8-171,17, т.е. это модальный интервал.

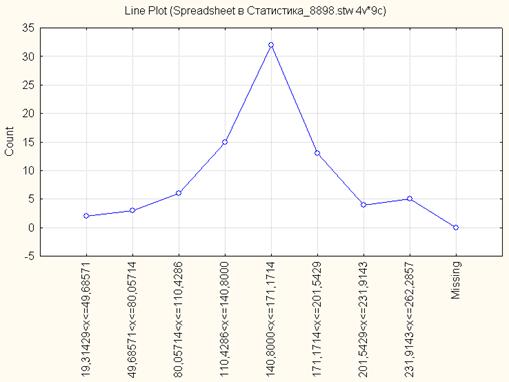
Рис. 1.2. Полигон распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г. в абсолютных частотах (n=8)

На рис. 1.3 приведена кумулята распределения в абсолютных частотах, а на рис. 1.4. тАУ в относительных частотах.

Из рисунка 1.2 видно, что середина распределения приходится на интервал 140,8-171,17, следовательно, этот интервал является медианным.

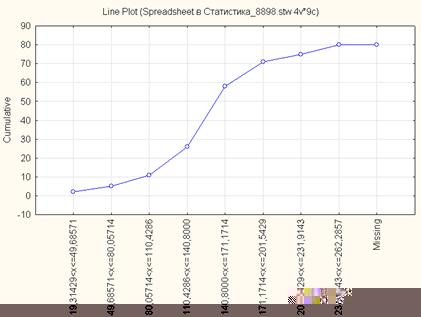
Рис. 1.3. Кумулята распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г., n=8 (абсолютные частоты)

Одной из часто используемых видов графиков является гистограмма (или столбиковая диаграмма), т.е. график распределения, на котором частоты каждого интервала представлены в виде столбиков (рис. 1.5).

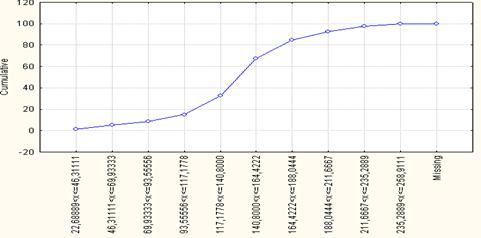
Рис. 1.4. Кумулята распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г., n=8 (относительные частоты)

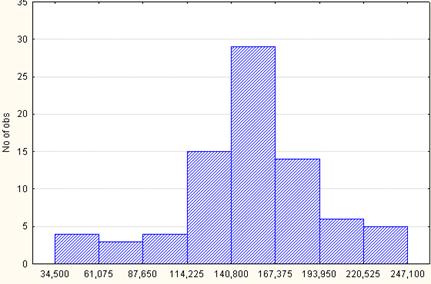
Рис. 1.5. Гистограмма распределения количества легковых автомобилей на 1000 чел. населения по регионам России за 2005 г. (n=8)

2. ХАРАКТЕРИСТИКА ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

РАСПРЕДЕЛЕНИЯ

Статистический анализ вариационных рядов распределения предполагает расчет характеристик центра распределения, его структуры, оценку степени вариации и дифференциации изучаемого признака, изучение формы распределения.

В качестве показателей центральной тенденции распределения используются: среднее арифметическое значение, мода и медиана.

Средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Иными словами, средняя арифметическая величина тАФ среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности[4]
.

Средняя арифметическая определяется по формулам:

1) Средней арифметической простой (для несгруппированных данных):

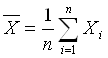,(2.1)

где: тАУ значение признака у i-й единицы совокупности; n тАУ объем совокупности (Valid N).

2) Средней арифметической взвешенной (для интервального вариационного ряда):

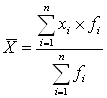, (2.2)

где:f_i тАУ абсолютные частоты; x_i тАУ середина интервала.

Определим среднюю арифметическую для рассматриваемых данных:

1. По формуле простой средней на основе массива несгруппированых данных:

2. По формуле средней арифметической взвешенной на основе группировочной таблицы с 8 интервалами (табл. 2.1):

Таблица 2.1 Расчет средней арифметической взвешенной для распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г.

Интервал	Абсолютная частота (fi)	Середина интервала (xi)
19,31429-49,68571	2	34,5	69
49,68571-80,05714	3	64,871425	194,6143
80,05714-110,4286	6	95,24287	571,4572
110,4286-140,8	15	125,6143	1884,215
140,8-171,1714	32	155,9857	4991,542
171,1714-201,5429	13	186,35715	2422,643
201,5429-231,9143	4	216,7286	866,9144
231,9143-262,2857	5	247,1	1235,5
Итого:	80	тАУ	12235,89

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Аналитическая теория чисел. L-функция Дирихле

Арифметичнi застосування теорii конгруенцiй