Арифметичнi застосування теорii конгруенцiй

Курсова робота

АРИФМЕТИЧНРЖ ЗАСТОСУВАННЯ ТЕОРРЖРЗ КОНГРУЕНЦРЖЙ

Змiст

Вступ

1. Конгруенцii та iх основнi властивостi

2. Ознаки подiльностi

3. Перевiрка арифметичних дiй

4. Визначення члена цифр перiоду при перетвореннi звичайного дробу в десятковий

5. РЖндекси. Загальнi властивостi

Висновки

Важливе мiсце в курсi теорii чисел посiдають конгруенцii та, зокрема, застосування конгруенцiй. Цим питанням займалися такi видатнi вченi як, Ейлер, Ферма, Б. Паскаль.

П'iр Ферма (1601-1665) - вiдомий свого часу юрист i радник судового парламенту в Тулузi - iнтенсивно i з великим успiхом займався рiзними математичними питаннями. П. Ферма i одним з творцiв диференцiального числення i теорii ймовiрностi, але особливо велике значення мають його роботи по теорii чисел. Бiльшiсть теоретико-числових результатiв П. Ферма записувалися ним на полях екземпляра твору Дiофанта тАЮАрифметикатАЭ; Ферма зазвичай не записував доведення, а давав тiльки короткi вказiвки про метод, який вiн застосовував для отримання свого результату. Твiр Ферма пiд назвою тАЮOpera Varia" були виданi вперше в 1679 р.

Теорема Ферма, викладена в цiй главi, була висловлена в одному з листiв, посланому iм в 1640 р. Френiклу. У цьому листi Ферма пише, що вiн отримав доведення цiii теореми; проте саме доведення не було ним опублiковане.

Перше з вiдомих доведень теореми Ферма належить Лейбнiцу (1646-1716). Доведення Лейбнiца було засноване на розглядi порiвняння:

.

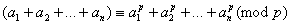Ейлер дав декiлька рiзних доведень теореми Ферма, з яких перше вiдноситься до 1736 р. У 1760 р. Ейлер узагальнив теорему, надавши iй вигляду теореми 120, що носить його iм'я. Треба при цьому мати на увазi, що термiнологiя i позначення у Ферма i у Ейлера абсолютно вiдмiннi вiд сучасних.

Блез Паскаль (1623-1662) - видатний французький математик, фiзик i фiлософ. Математичнi iнтереси Паскаля дуже рiзноманiтнi: вiн зробив iстотний внесок у розвиток аналiзу нескiнченно малих; разом з Ферма Паскаль i основоположником теорii ймовiрностей; йому належать загальна ознака подiльностi будь-якого цiлого числа на будь-яке iнше цiле число, яка ТСрунтуiться на знаннi суми цифр числа, а також спосiб обчислення бiномiальних коефiцiiнтiв ("Арифметичний трикутник ″); вiн вперше точно визначив i застосував для доведення метод повноi математичноi iндукцii

Дана курсова робота складаiться з 5 параграфiв:

1. Конгруенцii та iх основнi властивостi: вводяться означення конгруенцii, основнi властивостi, основнi теоремами в теорii конгруенцiй - Ейлера i Ферма.

2. Ознаки подiльностi. В цьому параграфi розглядаються основнi ознаки подiльностi цiлих чисел, при використаннi конгруенцiй; метод Паскаля - загальна ознака подiльностi будь-якого цiлого числа на будь-яке iнше цiле число.

3. Перевiрка арифметичних дiй. В даному параграфi наведено два способи перевiрки арифметичних дiй: "перевiрки за допомогою дев'ятки", " перевiрки за допомогою одинадцяти".

4. Визначення члена цифр перiоду при перетвореннi звичайного дробу в десятковий. Використовуючи конгруенцii можна перетворити десятковий дрiб у звичайний i визначити перiод даного дробу.

5. РЖндекси. В цьому параграфi розглядають основнi властивостi iндексiв, iх загальна характеристика. РЖндекси по простому i складеному модулю розглядаються в окремих пiдпунктах.

Кожен параграф проiлюстровано прикладами.

Припустимо, що т i натуральне число; розглядатимемо цiлi числа у зв'язку з остачами вiд дiлення iх на це натуральне 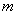Ваяке називають модулем. Згiдно з теоремою про дiлення з остачею кожному числу а вiдповiдатиме певна остача i вiд дiлення а на т:

, .

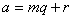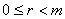Якщо двом цiлим числам 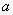Ваi Вавiдповiдаi одна й та сама остача 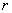Вавiд дiлення iх на т, то вони називаються конгруентними (або порiвнянними) за модулем т. Це позначаiться символом:

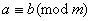Ва(1)

читаiться: а конгруентне з Ваза модулем т.

Деякi автори позначають це коротше:

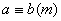Ва(1')

Спiввiдношення (1) [або (1')] мiж числами називають конгруенцiiю, або порiвнянням.

Приклади. ; ; .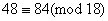

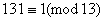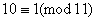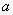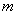Теорема 1. Конгруентнiсть чисел Ваi Ваза модулем Варiвнозначна:

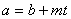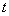а) можливостi подати а у формi , де Ва- цiле;

б) подiльностi 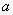Ва- Вана .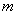

Властивостi:

1. Для конгруенцii справджуються закони: рефлективностi, симетричностi i транзитивностi, тобто вiдповiдно:

a) ;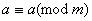

б) з конгруенцii 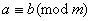Вавипливаi, що ;

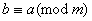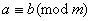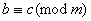в) якщо Ваi , то .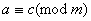

2. Конгруенцii за одним i тим самим модулем можна почленно додавати (або вiднiмати).

Висновок 1. Доданок, що стоiть у якiй-небудь частинi конгруенцii, можна переносити в iншу частину, змiнивши знак на протилежний.

Висновок 2. Можна додати до обох частин або вiдняти вiд обох частин конгруенцii одне й те саме число.

Висновок 3. До кожноi частини конгруенцii можна додати (або вiдняти вiд неi) довiльне число, кратне модулю.

3. Конгруенцii за одним i тим самим модулем можна почленно перемножати.

Висновок 1. Обидвi частини конгруенцii можна помножити на одне й те саме цiле число.

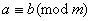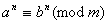Висновок 2. Обидвi частини конгруенцii можна пiдносити до одного й того самого цiлого невiд'iмного степеня, тобто якщо. , то , де 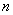Ва- цiле.

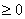4. Обидвi частини конгруенцii можна подiлити на iхнiй спiльний дiльник, якщо вiн взаiмно простий з модулем.

5. Обидвi частини конгруенцii i модуль можна помножити на одне й те саме натуральне число.

6. Обидвi частини конгруенцii i модуль можна подiлити на будь-який iхнiй спiльний дiльник.

7. Якщо конгруенцiя маi мiсце за кiлькома модулями, то вона матиме мiсце i за модулем, що дорiвнюi iхньому найменшому спiльному кратному.

теорiя конгруенцiя ейлер ферм

8. Якщо конгруенцiя маi мiсце за модулем 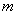, то вона матиме мiсце i за будь-яким дiльником 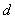Вацього модуля.

9. Якщо одна частина конгруенцii i модуль дiляться на яке-небудь цiле число, то i друга частина конгруенцii дiлиться на це число.

10. Числа 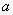Ваi , конгруентнi мiж собою за модулем 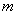, мають з ним один i той самий найбiльший спiльний дiльник.

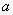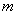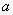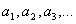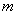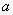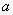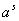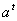Вiзьмемо деяке натуральне число , взаiмно просте з модулем , розглянемо послiдовнi степенi : . Всi числа цiii нескiнченноi множини розподiленi в Вакласах, отже, принаймнi один з цих класiв повинен мiстити нескiнченну множину степенiв . Узявши з цього класу два степенi Ваi позначивши iх Ваi , де 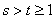, матимемо 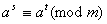. Оскiльки з 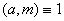Васлiдуi 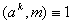, то 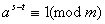. Таким чином, для деяког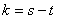о маiмо 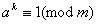, причому оскiльки 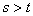Вато 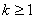. Тодi i при будь-якому натуральному 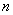Ваматимемо 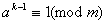, що доводить iснування нескiнченноi множини степенiв 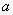, що належать класу .

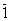П. Ферма для простого модуля, а Л. Ейлеру для будь-якого модуля вдалося вказати значення 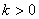, при яких маi мiсце рiвнiсть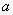 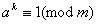. Вiдповiднi теореми, ми iх називатимемо теоремами Ферма - Ейлера, i основою всiii теорii порiвнянь i широко використовуються як в теоретичних дослiдженнях, так i в арифметичних застосуваннях.

Теорема Ферма. Для будь-якого простого 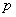Ваi будь-якого 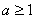, що не дiлиться на 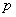, справедливе порiвняння

.

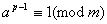Теорема Ейлера. Для будь-якого модуля 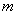Ваi будь-якого 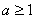, взаiмно простого з 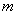, справедливе порiвняння

.

Розрiзняють загальнi ознаки, що мають силу для будь-якого m i власнi - для окремих значень m.

Загальну ознаку подiльностi виражаi правило, за допомогою якого по цифрах числа N записаного в системi числення з основою g, можна судити про подiльнiсть його на iнше число m.

Французький математик Блез Паскаль (1623-1662) знайшов загальну ознаку подiльностi. РЗi можна сформулювати наступним чином:

Теорема 7 (загальна ознака подiльностi Паскаля). Для того, щоб число N, записане в довiльнiй g-iтiй системi числення у виглядi:

,

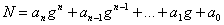дiлилося на число m, необхiдно i достатньо, щоб число 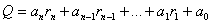Вадiлилося на m (де 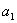Ва- цифри числа N, а 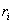Ва- абсолютно найменшi вирахування вiдповiдних степенiв 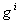Вапо модулю m, i = 1, 2.,n). Доведення. Нехай 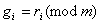, де 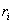Ва- абсолютно найменше вирахування числа 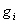Вапо модулю m, (i = 1, 2., n). Тодi

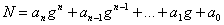
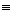
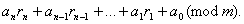Ва(1)

Число N дiлиться на m тодi i тiльки тодi, коли

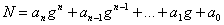
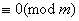Ва(2)

З рiвнянь (1) i (2) i iх транзитивностi отримуiмо умову, рiвносильну умовi (2):

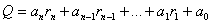
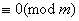. (3)

З доведеного випливаi: для того, щоб N дiлилося на т, необхiдно i достатньо, щоб Q дiлилося на m.

Теорема доведена.

Як наслiдок iз загальноi ознаки Паскаля витiкають рiзнi ознаки подiльностi. Розглянемо деякi з них (найчастiше використовуванi на практицi).

Наслiдок 1. Нехай m - дiльник числа g - 1. Для того, щоб число, записане в g-iтiй системi числення, дiлилося на m, необхiдно i достатньо, щоб сума його цифр дiлилася на m.

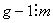Доведення. В даному випадку , а ; тодi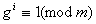, тобто, 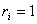а тому:

.

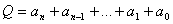Таким чином, для того, щоб N дiлилося на m, необхiдно i достатньо, щоб сума цифр цього числа дiлилася на m.

Для чисел, записаних в десятковiй системi, з формульованоi ознаки випливають вiдомi ознаки подiльностi на 9 i 3.

Наслiдок 2. Нехай m - дiльник числа g + I. Для того, щоб число, записане в g-iтiй системi числення, дiлилося на m, необхiдно i достатньо, щоб рiзниця мiж сумами цифр на парних i непарних мiсцях дiлилася на m.

Доведення. В даному випадку Звiдси витiкаi затвердження слiдства. Для чисел, записаних в десятковiй системi, отримуiмо 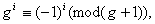Ваа 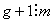; тодi 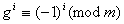, тобто 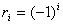, а тому .

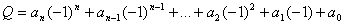Для чисел, записаних в десятковiй системi, отримуiмо вiдому ознаку подiльностi на 11: для того, щоб число дiлилося на 11, необхiдно i достатньо, щоб рiзниця мiж сумами цифр на парних i непарних мiсцях дiлилася на 11. Наприклад, число 25 697 058 не дiлиться на 11, оскiльки рiзниця (2 + 6 + 7 + 5) - (5 + 9 + 0 + 8) = 20-22 == - 2 не дiлиться на 11.

Число 905 784 дiлиться на 11.

Наслiдок 3. Нехай m - дiльник числа 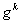. Для того, щоб число, записане в g-iтiй системi числення, дiлилося на m, необхiдно i достатньо, щоб число, записане останнiми k цифрами даного числа, дiлилося на m.

Доведення. В даному випадку 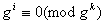для 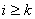Вадо, а тому

.

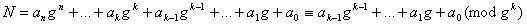Або

. (*)

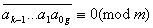З (*) витiкаi твердження наслiдку.

Для чисел, записаних в десятковiй системi, iз наслiдку 3 випливаi цiлий ряд ознак подiльностi.

1) Основа 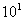Ва(де 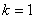) дiлиться на 2, 5, 10.

В цьому випадку отримаiмо ознаки подiльностi на 2, 5, 10.

а) Для подiльностi числа на 2 необхiдно i достатньо, щоб остання цифра була парною.

б) Для подiльностi числа на 5 необхiдно i достатньо, щоб остання цифра дiлилася на 5 (остання цифра 0 або 5).

в) Для подiльностi числа на 10 необхiдно i достатньо, щоб воно закiнчувалося нулем.

2) Дiльником числа 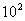Ва(де 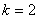) i числа 4, 25, 50, 100.

Застосовуючи наслiдок 3, отримуiмо ознаки подiльностi на 4, 25, 50, 100.

Зокрема, для того, щоб число дiлилося на 4, необхiдно i достатньо, щоб число, записане останнiми двома (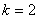) цифрами, дiлилося на 4.

3) Аналогiчно можна вивести ознаки подiльностi на дiльникiв числа 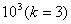, тобто на числа 8, 125,. Тут потрiбно розглядати число, записане останнiми трьома цифрами даного числа.

Теорема 8. Для того, щоб число дiлилося на 7, або на 11, або на 13, необхiдно i достатньо, щоб рiзниця мiж числом записаним останнiми трьома цифрами, i числом, записаним цифрами, якi залишилися даного числа (або навпаки), дiлилася на 7, або на 11, або на 13.

Доведення. Будь-яке число N можна представити у виглядi 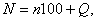Ваде 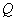Ва- число, записане останнiми трьома цифрами числа N, а n - цифрами, якi залишилися (приклад: 829 296 = 829 1000 + 296).

Запишемо N так:

;

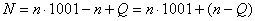звiдси отримаiмо:

,

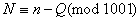чи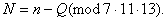

З (4) слiдуi висновок: для того, щоб число N дiлилося на 7, або на 11, або на 13, необхiдно i достатньо, щоб число n - Q (або Q - n) дiлилося на 7, або на 11, або на 13.

Приклади.

1. Чи дiлиться число 56 704 на одне з чисел: 7, 11, 13? Знаходимо: Q - n = 704 - 56 = 648. Але число 648 не дiлиться нi на 7, нi на 11, нi на 13; отже, i дане число не дiлиться нi на одне з чисел: 7, 11, 13.

2. Чи дiлиться число 454 111 на 7?

454 - 111 = 343, 343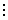7; отже, 454 111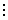7.

Теорiя порiвнянь даi наступний спосiб перевiрки арифметичних дiй. Вибираiмо деякий модуль m i замiнюiмо великi числа а, b, c, над якими нам треба виконуiмо дii (додавання, вiднiмання, множення, пiднесення до степеня), невеликими числами а', b', с' порiвнянними з ними по модулю m. Виконавши дii над а, b, c ми такi ж дii виконуiмо над а', b', с', якщо дii виконанi правильно, то результати цих дiй над а, b, c,. i над а', b', с',. мають бути порiвняннi по модулю m.

Дiйсно, згiдно за властивостями якщо

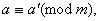
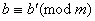тАж,

то

,

.

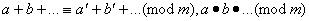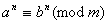Для перевiрки спiввiдношення 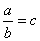Вапредставляiмо його у виглядi 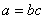. Використання цього способу перевiрки, звичайно, маi сенс лише тодi, коли знаходження таких чисел а', b', с' може бути здiйснено легко i швидко. Для цього зазвичай як модуль m вибирають m=9 або m=11. Кожне число, записане в десятковiй системi числення, порiвнюiмо з сумою його цифр по модулю 9, так що ми можемо сформулювати наступний спосiб тАЮперевiрки за допомогою дев'ятки".

Для кожного числа обчислюiться остача вiд дiлення на 9 суми цифр. Виконуючи дii над числами, виконуiмо такi ж дii над цими остачами. Результат даних дiй над цими остачами повинен вiдрiзнятися вiд суми цифр шуканого результату на число, кратне дев'яти.

Звичайно, якщо помилка така, що рiзниця мiж знайденою i дiйсною величинами кратна 9, то вона при цьому способi перевiрки не буде помiчена. По модулю m = 11 кожне число, записане в десятковiй системi числення, буде порiвнянне з сумою цифр, узятих справа. налiво поперемiнно iз знаками тАЮплюс" i тАЮмiнус"; тому ми можемо сформулювати наступний спосiб тАЮперевiрки за допомогою одинадцяти". Для кожного числа обчислюiться остача вiд дiлення на 11 суми цифр, узятих поперемiнно справа налiво зi знаками тАЮплюс" i тАЮмiнуi". Результат даних дiй над цими остачами повинен вiдрiзнятися вiд суми узятих поперемiнно зi знаками тАЮплюс" i тАЮмiнус" справа налiво цифр шуканого: результату на число, кратне 11. Якщо помилка буде кратна 11, вона не буде помiчена при цьому способi.

При складних обчисленнях маi сенс проводити двi перевiрки: одну за допомогою модуля 9, а iншу за допомогою модуля 11. В цьому випадку помилка не буде помiчена лише, якщо вона кратна 99, що, звичайно, буваi дуже рiдко.

Приклади.1) Перевiрити за допомогою модуля 9, чи вiрний результат множення 734168539 = 626 899224.

Знаходимо, що сума цифр першого множника 21=3 (mod 9), а другого 25 = 7 (mod 9). Сума цифр добутку дорiвнюi 48 i дiйсно вiдрiзняiться вiд 37 = 21 на число, кратне 9.

2) З допомогою, модуля 11 перевiрити результат:

.

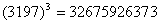Сума цифр основи, узятих поперемiнно iз знаками тАЮплюс" i тАЮмiнус", 7-9+1-3 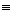Ва7 (mod 11). Вiдповiдна сума для результату, рiвна - 9, вiдрiзняiться вiд 73 = 343 на число, кратне одинадцяти.

3) Перевiрити за допомогою модулiв 9 i 11, чи вiрно, що:

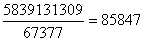
Сума цифр дiленого 42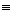6 (mod 9), дiльника 30 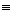Ва3 (mod 9) i частки 32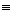5 (mod 9). Добуток 35=15 вiдрiзняiться вiд 6 на число, кратне 9. Перевiряiмо за допомогою модуля 11. Знакозмiнна сума цифр дiленого, дiльника i частки рiвнi вiдповiдно 22, 2 i 14. Добуток 214 = 28 вiдрiзняiться вiд 22 на число, не кратне 11, так що результат не вiрний.

З елементарноi арифметики вiдомо, що звичайний нескоротний дрiб у перетворюiться в скiнченний десятковий дрiб тодi i тiльки тодi, коли канонiчний розклад знаменника не мiстить простих множникiв вiдмiнних вiд 2 i 5.

Нехай 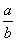Ванескоротний дрiб i канонiчний розклад знаменника Вамiстить простi числа, вiдмiннi вiд 2 i 5; перетворюватимемо такий дрiб у десятковий.

Нескiнченний десятковий дрiб, десятковi знаки якого перiодично повторюються, називаiться перiодичним, десятковим дробом. Якщо десятковi знаки повторюються, починаючи з першого, то десятковий дрiб називаiться чистим перiодичним, у противному разi вiн називаiться мiшаним перiодичним дробом.

Теорема 1. Якщо 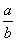нескоротний дрiб i (,

10) = 1, то цей дрiб перетворюiться у чистий перiодичний десятковий дрiб; число цифр у перiодiдробу дорiвнюi 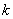, де 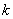Ва- показник, до - якого належить число 10 за модулем .

Доведення. Справдi, не порушуючи загальностi мiркувань, можна нескоротний дрiб 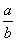Вавважати правильним (якщо вiн неправильний, тобто

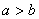, то. ми спочатку видiлимо цiлу частину); отже, 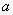можна вважати рiвним одному з 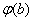Вачисел, менших Ваi взаiмно простих з .

Перетворюватимемо дрiб 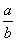Вау десятковий за загальними правилами:

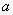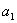для цього подiлимо спочатку 10 на Вапозначаючи через Вачастку i через 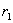Ва- остачу вiд цього дiлення, отримаiмо:

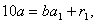
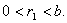
Тепер подiлимо 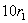Вана :

;

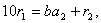
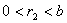далi дiлимо 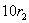Вана :

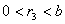
i т.д. Такий процес нескiнченний, бо щоразу будуть остачi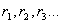, меншi вiд Ваi взаiмно простi з . Справдi, 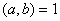, 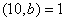Ваза умовою, тому 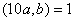Ваi 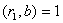; аналогiчно 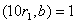, а тому 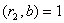Ваi т.д.

Звiдси випливаi, що рiзних остач при зазначеному дiленнi буде не бiльш, як 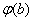. Це означаi, що не пiзнiш як через 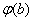Вакрокiв ми дiстанемо повторення остач, а отже, й повторення цифр частки.

Для доведення теореми залишаiться показати, що перше повторення настане пiсля 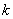Вадiлень, де 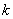Ва- показник, до якого належить 10 за модулем Вапричому перша остача, яка повторюiться, саме и буде 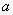. Тому знайдений дрiб буде чистим перiодичним з числом цифр у перiодi, яке дорiвнюi .

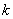Але для доведення цих тверджень досить встановити, що коли Ва- найменший показник, для якого

, (1)

то при дiленнi на Вабудь-якого числа 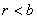Ваi взаiмно простого з Ваостача 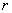Ваповториться тiльки пiсля визначення 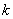Вацифр частки.

Справдi, конгруенцiя (1) еквiвалентна конгруенцii:

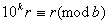. (2)

Ця конгруенцiя саме й показуi, що приписавши до числа 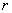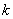Ванулiв, що вiдповiдаi визначенню 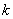Вапослiдовних цифр частки, дiстанемо при дiленнi 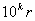Вана Ваостачу 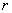. Через те що 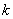-найменше невiд'iмне число, для якого мають мiсце конгруенцii (1) i (2), то жодна остача не може повторитись ранiш як через 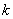Вадiлень. Зокрема, при дiленнi 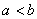Вана Ваперша остача, що повторюiться, саме й буде 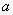Вапричому вона повториться точно через 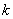Вадiлень. Цим теорему доведено.

Бачимо, 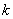Вазалежить тiльки вiд знаменника нашого дробу i, звичайно, вiд основи нашоi системи числення, тобто вiд числа g = 10. Тому два дроби 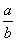Ваi 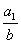, якi задовольняють умову теореми 1, матимуть одну й ту саму довжину перiоду при перетвореннi iх у десятковi дроби.

Приклад. Знайти довжину перiоду, який утворюiться при перетвореннi дробiв 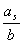, де 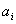Ва- будь-яке цiле, взаiмно-просте з 21 у десятковi. Тут 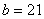; дiлимо:

У частцi маiмо 6 цифр, беручи до уваги й 0, який вiдповiдаi першiй дев′ятцi. Отже, 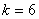, тобто шуканий перiод складаiться з 6 цифр.

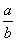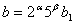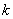Теорема 2. Якщо нескоротний дрiб i , де , то цей дрiб перетворюiться у мiшаний перiодичний десятковий дрiб; число цифр у перiодi дробу дорiвнюi де 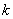Ва- показник, якому належить 10 за модулем ; число цифр до перiоду дорiвнюi 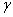Ваде 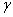Ва- найбiльше з чисел 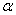Ваабо .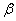

Доведення. Справдi, нехай дрiб 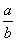Ва- нескоротний, причому

,

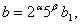
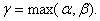
Помножимо 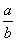Вана 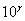; пiсля скорочення в знаменнику множникiв 2 i 5 отримаiмо:

,

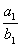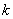де дрiб Ва- нескоротний i . За теоремою 1, цей дрiб перетворюiться у чистий перiодичний з числом цифр у перiодi, яке дорiвнюi , де 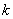Ва- показник, до якого належить 10 за модулем 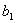. Щоб з нього дiстати дрiб 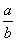, треба 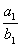Ваподiлити на 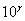, тобто перенести кому в знайденому перiодичному дробi на 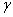Вазнакiв лiворуч. У результатi отримаiмо мiшаний перiодичний дрiб з числом цифр до перiоду, що дорiвнюi 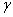. Цим теорему доведено.

Приклад. 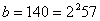; маiмо 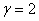. Знайдемо 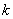, тобто показник, до якого належить 10 за модулем 7. Маiмо:

.

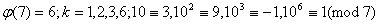Отже, 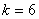Ва(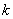 можна знайти згiдно з зауваженням зробленим вище). Таким способом усi дроби виду 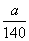, де 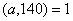, перетворюються в мiшанi перiодичнi дроби з числом цифр у перiодi, яке дорiвнюi 6, i з числом цифр до перiоду яке дорiвнюi 2. Так наприклад, безпосередньо переконуiмось, що

.

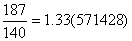Розглянемо обернену задачу: знайти звичайний дрiб, який вiдповiдаi заданому перiодичному дробу.

Нехай дано чистий перiодичний дрiб: 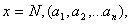де 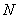Ва- цiла частина, тобто

,

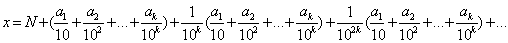або

;

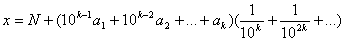але

,

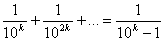де число 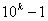Вазображаiться 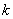Вадев'ятками. Отже отримаiмо:

,

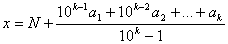тобто для того, щоб перетворити чистий перiодичний дрiб у звичайний, треба перiод дробу зробити чисельником, а в знаменнику написати стiльки дев'яток, скiльки цифр у перiодi, i знайдений дрiб додати до цiлоi частини. Нехай тепер дано мiшаний перiодичний дрiб:

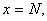
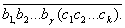
Його можна подати так:

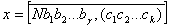
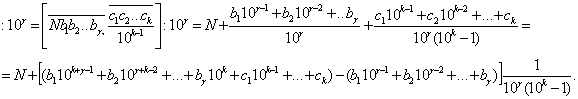
Звiдси виводимо таке правило: щоб перетворити мiшаний перiодичний дрiб у звичайний, треба вiд числа, що стоiть мiж комою i другим перiодом (тобто вiд числа 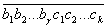), вiдняти число, яке стоiть мiж комою i першим перiодом (тобто число 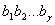), i цю рiзницю зробити чисельником; у знаменнику треба написати стiльки дев'яток, скiльки цифр у перiодi, й пiсля них - стiльки нулiв, скiльки цифр мiж комою й першим перiодом, i цей дрiб додати до цiлоi частини N.

Зауваження. Можна вiдразу перетворити перiодичний дрiб у звичайний неправильний дрiб (не видiляючи цiлоi частини). Для цього треба цифри цiлоi частини вважати цифрами, що стоять до перiоду, й застосувати правило для перетворення мiшаного перiодичного дробу в звичайний. При такiй побудовi знаменника цифри цiлоi частини враховувати не слiд.

Приклад.

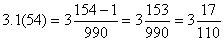, або .

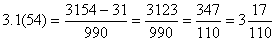Загальновiдомо, яке велике значення в рiзних роздiлах математики i особливо в обчислювальнiй практицi мають логарифми. У теорii чисел вводиться схожий з логарифмами апарат, який ми називатимемо iндексами. Логарифмом b за основою а, як вiдомо, називаiться показник степеня а, рiвний b. У теорii чисел аналогiчно цьому розглядають показник степеня а, порiвнянною з b по даному модулю m, i такий показник називають iндексом b по модулю m i основою а.

Означення 1. Нехай (а,m) = l, (b,m) = 1; число s називаiться iндексом b по модулю m i основою а, якщо

Таким чином, згiдно з означенням:

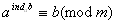. (1)

Якщо 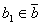, то з Васлiдуi також , тобто iндекс числа b i також iндексом i всiх чисел з 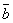, i ми можемо таке число s називати iндексом класу .

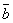Означення 2. Нехай (а, m) =l, (b, m) = 1. s називаiться iндексом класу 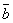Вапo модулю m i основою а, якщо по цьому модулю .

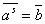Приклади. Нехай модуль m =13, основа а = 2, тодi 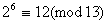, тобто 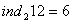, i для будь-якого 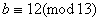Вабуде також 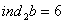, 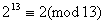тобто 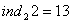, i в той же час, оскiльки 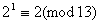, маiмо також .

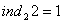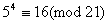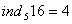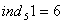Нехай модуль m = 21, основа а = 5. Тодi , , тобто по модулю 21 , . По цьому модулю 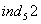Ване iснуi, оскiльки не iснуi s такого, що .

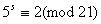Якщо як основу взяти число а, що не i первiсним коренем по модулю m, то iндекси будуть iснувати не для всiх чисел, взаiмно простих з модулем m.

Теорема 1. Нехай g-будь-який первiсний корiнь по модулю m. Для кожного числа b, взаiмно простого з модулем m, iснують iндекси за основою g, тобто iснують s такi, що

.

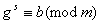Безлiч всiх таких iндексiв s для даного фiксованого b збiгаiться з не вiд′iмними числами деякого класу по модулю .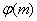

Властивостi:

1. Нехай g - первiсний корiнь по модулю m, (b,m) = 1; порiвняння

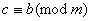Ва(2)

маi мiсце тодi i лише тодi, коли

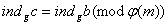. (3)

2. Нехай g - первiсний корiнь по модулю m

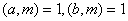. Тодi

.

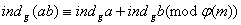3. Нехай g - первiсний корiнь по модулю m,

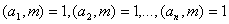. Тодi

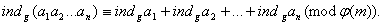Ва(5)

4. Нехай g - первiсний корiнь по модулю m, (а,m) = l, 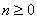; тодi

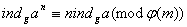. (6)

Означення 2. Якщо 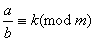, , 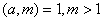то пiд 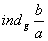Варозумiтимемо 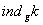, тобто iндекс будь-якого числа з класу 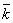Вапo модулю m.

5. Нехай g - первiсний корiнь по модулю 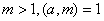; тодi

.

РЖндекси по простому модулю.

Особливо велике значення маi випадок, коли модуль - просте число. Оскiльки, по будь-якому простому модулю р iснують первiснi коренi, то, узявши за основу який-небудь з них, отримаiмо систему iндексiв, в якiй кожне число, що не дiлиться на р, матиме своi iндекси.

РЖндекси кожного такого числа згiдно з теоремою 1 i невiд′iмнi числа деякого класу по модулю р-1, а теореми а теореми 2-5 дають наступнi правила операцiй з iндексами по модулю р.:

якщо,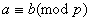

то 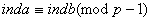, i, навпаки,

з 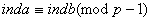Вавиходить .

.

.

.

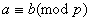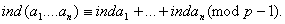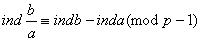Скорочено тут скрiзь опущений знак g, який вказуi основу, яка передбачаiться однаковою в лiвiй i правою частинах. Всi iндексованi числа передбачаються що дiляться на р.

По простому модулю р для кожного числа iснуi безлiч iндексiв, порiвнянних по модулю р - 1, i як iндекс можна брати будь-яке з них. Зазвичай зi всiх можливих значень iндексiв по данiй основi беруть найменше; при такому виборi iндексiв вони мають значення меншi нiж р - 1.

Таблицi iндексiв для простих модулiв р мiстять iндекси чисел вiд 1 до р - 1. Для кожного такого числа i всiх порiвнянних з ним по модулю р в таблицi вказуiться iндекс, який являi собою одне з чисел: 0,1., р - 1. У деяких таблицях як iндекс одиницi вказуiться не 0, а р - 1. Таблицi iндексiв складалися багатьма авторами. У 1839 р. таблицi iндексiв для простих чисел, менших чим 1000, були опублiкованi Якобi.

РЖндекси по складеному модулю.

Для складених модулiв вигляду 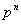Ваi 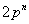, де р - просте число (р>2), iснують первiснi коренi

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Волоконно-оптические датчики температуры на основе решеток показателя преломления

Время и пространство - идеалистические понятия