Аналитическая теория чисел. L-функция Дирихле

Теория L-функций Дирихле развилась в одно из важнейших вспомогательных средств аналитической теории чисел. Большую роль в приложениях играет исследование нулей L-функций Дирихле.

В аналитической теории чисел L-функция Дирихле играет такую же роль, как и ζ-функция при решении задач теории чисел, а именно задач, связанных с распределением простых чисел в арифметических прогрессиях и в задачах, связанных с оценками арифметических сумм.

Предметом исследования данной курсовой работы является распределение значений L-функций Дирихле, результаты Гурвица о выводе функционального уравнения для L-функции Дирихле и как следствие, показать, что L-функции Дирихле в критической полосе имеют бесконечное число нулей. Эти функции ввел в 1837 г. Густав Дирихле при исследовании вопроса о распределении простых чисел в арифметических прогрессиях. Основные результаты были получены в 1922 году А. Гурвицем.

В данной курсовой работе изложение материала отражает основные свойства L-функций Дирихле и соответствует результатам, полеченным Гурвицем касающимся L-функций Дирихле.

В заключении данной работы приводится гипотеза о распределении нулей дзета-функции, сформулированная Бернхардом Риманом в 1859 году. Гипотеза Римана входит в список семи Влпроблем тысячелетияВ».

Вз1. Характеры Дирихле и L-функции Дирихле

Прежде всего определим характеры по модулю k, равному степени простого числа, и докажем их основные свойства. Характеры по произвольному модулю к определим затем через характеры по модулю, равному степени простого числа; при этом основные свойства последних сохранятся.

Пусть k=р^а, где р> 2 тАФ простое число, α≥1. Как известно, по модулю k существуют первообразные корни, и пусть g тАФ наименьший из них. Через ind n будем обозначать индекс числа п, (п, к) = 1, по модулю kпри основании g, т. е. число γ = γ(п) = ind n такое, что

(mod k).

Определение 1.1. Характером по модулю k= р^а, р>2 тАФ простое, α≥ 1, называется конечнозначная мультипликативная периодическая функция χ(n), областью определения которой является множество целых чисел п, и такая, что

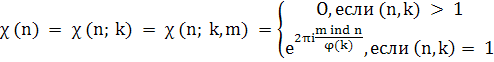
где т тАФ целое число.

Из определения характера видно, что функция зависит от параметра т, является периодической по т с периодом φ(k), т. е. существует, вообще говоря, φ(k) характеров по модулю k, которые получаются, если брать т равным 0, 1, .., φ(k) - 1.

Пусть теперь k = 2^α, α≥ 3. Как известно, для любого нечетного числа п
существует система индексов γ₀ = γ₀(п) и γ₁ = γ₁(n) по модулю k, т. е. такие числа γ₀ и γ₁ , что

Таким образом, числа γ₀ и γ₁ определяются с точностью до слагаемых, кратных соответственно 2 и 2^α-2.

Определение 1.2. Характером по модулю к = ^2α, α≥1, называется функция Ваобластью определения которой является множество целых чисел п, определенная одной из следующих формул:

Где m₀ , m₁ целые числа.

Из определения 1.2. видно, что функция Вазависит от параметров т₀ и m₁является периодической по m₀ и m₁, с периодами соответственно 2 и 2^α-2 т. е. существует, вообще говоря, φ(k), =< φ(k^α) характеров по модулю k = 2^α, которые получаются, если брать m₀ , равным 0, 1, а m₁ равным 0, 1, .., 2^α-2 - 1.

Ввиду того, что индекс числа или система индексов числа периодические с периодом, равным модулю функции, аддитивные, т. е. индекс произведения (соответственно система индексов произведения) равняется сумме индексов сомножителей (соответственно сумме систем индексов сомножителей), получаем следующие свойства характера χ (п):

1. Вапо модулю kтАФ периодическая с периодом k функция, т. е.

;

2. тАФмультипликативная функция, т. е.

Очевидно также, что

χ(1) = 1.

L-ряды Дирихле тАФ функции комплексного переменного, подобные дзета-функции Римана, введены Дирихле при исследовании вопроса о распределении простых чисел в арифметических прогрессиях. Везде ниже под L-рядом будем понимать L-ряд Дирихле.

Пусть k тАФ натуральное число и χ тАФ какой-либо характер по модулю k.

Определение 1.3. L-функцией называется ряд Дирихле вида:

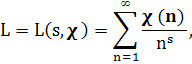
Ввиду того, что|χ(n)|≤1, следует аналитичность L(s, χ) в полуплоскости Re s>l. Для L(s, χ) имеет место аналог формулы Эйлера (эйлеровское произведение).

Лемма 1.1. При Re s > 1 справедливо равенство

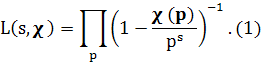
Доказательство. При X > 1 рассмотрим функцию

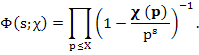
Так как Re s > 1, то

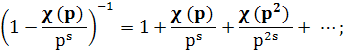
следовательно,

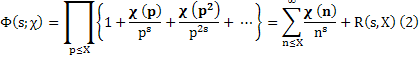
(воспользовались мультипликативностью χ(n) и однозначностью разложения натуральных чисел на простые сомножители). Далее,

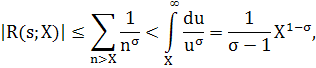
где σ=Re s>l. Переходя в (2) к пределу Х→+∞, получим утверждение леммы.

Из (1) находим

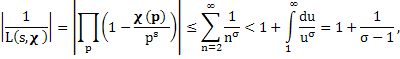
т. е. L(s, χ)≠0 при Re s>l. Если характер χ по модулю k является главным, то L(s, χ) лишь простым множителем отличается от дзета-функции ζ(s).

Лемма 1.2. Пусть χ(n) = χ ₀(n) по модулю k. Тогда при Re s> 1

Доказательство леммы следует из (6) и определения главного характера χ₀(n).

Следствие. L(s, χ) тАФ аналитическая функция во всей s-плоскости, за исключением точки s = 1, где она имеет простой полюс с вычетом, равным

Если характер χ(n) является производным, a χ₁(n) тАФ примитивный характер по модулю k₁, k_t\k, отвечающий χ(n), то L(s, χ)лишь простым множителем отличается от L(s, χ₁).

Лемма 1.3. Пусть χ₁тАФ примитивный характер по модулю k₁ и χ тАФ индуцированный χ₁ производный характер по модулю k, k_t ≠ k. Тогда при Re s > 1

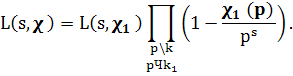
Доказательство леммы следует из (1) и свойств χ₁ и χ.

Функцию L(s, χ) можно продолжить в полуплоскость Re s > 1

Лемма 1.4. Пусть χ≠χ₀, тогда при Re s>0 справедливо равенство

Где

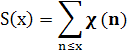
Доказательство. Пусть N ≥1, Re s>l. Применяя преобразование Абеля, будем иметь

Где

Переходя к пределу N → +∞, получим (8) при Re s>l. Но |S(x)|≤φ(k); поэтому интеграл в (3) сходится в полуплоскости Re s > 0 и определяет там аналитическую функцию, что и требовалось доказать.

Вз2. Функция θ(x ,χ), её функциональное уравнение

Функциональное уравнение будет получено для L(s, χ)с примитивным характером χ; тем самым и в силу леммы 3 L(s, χ) будет продолжена на всю s-плоскость при любом χ. Вид функционального уравнения зависит от того, четным или нечетным является характер χ, т. е. χ(-1)=+1 или χ(-1)=тАУ1

Прежде чем вывести функциональное уравнение для L(s, χ) и продолжить L(s, χ) на всю s-плоскость, докажем вспомогательное утверждение, аналогичное функциональному уравнению для θ(х) (см. лемму 3, IV).

Лемма 2.1. Пусть χ тАФ примитивный характер по модулю k. Для четного характера χ определим функцию θ (x, χ) равенством

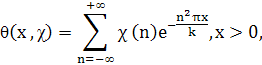
а для нечетного характера х определим функцию θ₁(x, χ) равенством

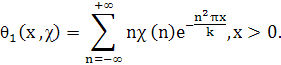
Тогда для введенных функций θ (x, χ) и θ₁(x, χ) справедливы следующие соотношения (функциональные уравнения):

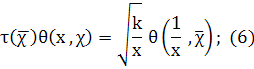
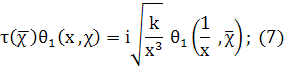
где τ(χ) тАФ сумма Гаусса.

Доказательство. Воспользуемся доказанным в лемме 3, IV равенством

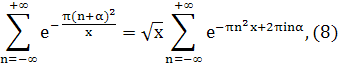
где x > 0, α тАФ вещественное.

Имеем

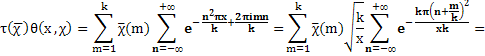
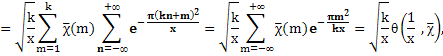
что доказывает равенство (6).

Чтобы доказать равенство (7), продифференцируем почленно (8) и заменим x на х/к, α на m/k (указанные ряды можно почленно дифференцировать, так как получающиеся после этого ряды равномерно сходятся). Получим

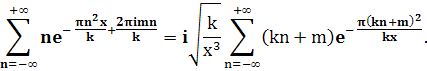
Отсюда, как и выше, выводим

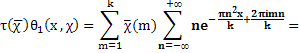
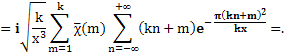
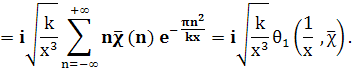
Лемма доказана.

Вз3. Аналитическое продолжение L-функции Дирихле на комплексную плоскость

Получим аналитическое продолжение функции L(s, χ) в область Re s >0.

Лемма 3.1.Пусть χ(n) тАУ неглавный характер по модулю m,

Тогда при Re s > 1 справедливо равенство

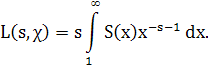
Доказательство. Пусть N≥1, Re s >1 . Применяя частное суммирование, будем иметь

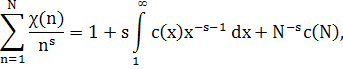
Где c(x)=S(x)-1. Так как |c(x)|≤x , то, переходя к пределу N, получим

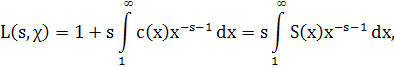
Что и требовалось доказать.

Вз4. Функциональное уравнение для L-функции Дирихле. Тривиальные нули L-функции Дирихле

Теорема 4.1. (функциональное уравнение). Пусть χтАФ примитивный характер по модулю k,

Тогда справедливо равенство

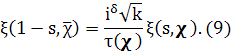
Доказательство, потАФсуществу, повторяет вывод функционального уравнения для дзета-функции (теорема 1, IV).

Предположим, что χ(-1)=+1. Имеем

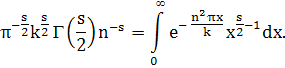
Умножая последнее равенство на χ (п) и суммируя по п, при Re s > 1 получим

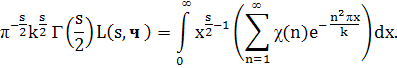
Ввиду того, что χ тАФ четный характер, имеем

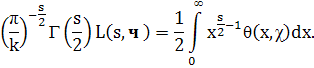
Разбивая последний интеграл на два, производя в одном из них замену переменной интегрирования (х → 1/х) и пользуясь (6), найдем

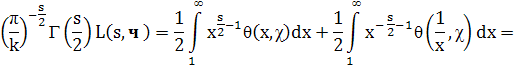
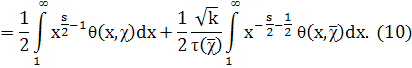
Правая часть этого равенства является аналитической функцией при любом s и, следовательно, дает аналитическое продолжение L(s, χ) на всю s-плоскость. Так как Г(s/2)≠0, то L(s, χ) тАФ регулярная всюду функция. Далее, при замене s на 1 тАФ s и χ на , правая часть (10) умножается на , так как χ(тАФ 1)=1 и, следовательно, τ(χ) τ()= τ(χ) = k. Отсюда получаем утверждение теоремы при δ = 0.

Предположим, что χ(тАФ1) = тАФ1. Имеем

Следовательно, при Re s > 1

Последнее равенство дает регулярное продолжение L(s, χ) на всю s-плоскость; правая часть его при замене s на 1 тАФ s и χ на, умножается на iВаввиду того, что

τ(χ) τ()= тАФk.

Отсюда получаем утверждение теоремы при δ = 1. Теорема доказана.

Следствие. L(s, χ) тАФ целая функция; если χ (тАФ1) = +1, то единственными нулями L(s, χ) при Re s ≤ 0 являются полюсы Г , т. е. точки s = 0, тАФ2, тАФ4, ..;

если χ (тАФ1) = тАФ1, то единственными нулями L(s, χ) при Re s ≤ 0 являются полюсы Г Ват. е. точки s = тАФ1, тАФ3, тАФ5, . .

дирихле тривиальный вейерштрасс риман

Вз5. Нетривиальные нули L-функции Дирихле

Тривиальные нули L-функции Дирихле

ξ(s, χ) тАФ целая функция; если χ (тАФ1) = +1, то единственными нулями L(s, χ) при Re s≤0 являются полюсы ,т. е. точки s =0, тАФ2. тАФ4, ..; если χ (тАФ1) = тАФ1, то единственными нулями L(s, χ) при Re s≤0 являются полюсы Ват.е. точки s = тАФ1,-3, -5, . .

5.1 Теорема Вейерштрасса о разложении в произведение целых функций

Теорема 5.1. Пусть a₁, .., а_п, .. тАФ бесконечная последовательность комплексных чисел, причем

0< |a₁| ≤ |a₁| ≤..≤|а_n|<..

И limВа= 0.

Тогда существует целая функция G(s), которая имеет своими нулями только числа а_п (если среди а_п есть равные, то нуль G(s) будет иметь соответствующую кратность).

Следствие 5.1. Пусть последовательность чисел a₁, .., а_п, .. удовлетворяет условиям теоремы 5.1., и, кроме того, существует целое число р > 0 такое, что сходится ряд

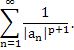
Тогда функция G₁(s),

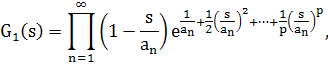
удовлетворяет теореме5. 1.

Теорема 5.2. Каждая целая функция G(s) может быть представлена в виде

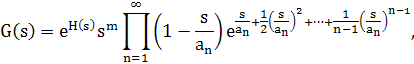
где H(s) тАФ целая функция, а числа 0, a₁ ,a₂, .., атАж,-тАФ нули G(s), расположенные в порядке возрастания их модулей. Если, кроме того, последовательность а_n , п = 1,2,.., удовлетворяет условиям следствия 5.1., то

Доказательство. Нули G(s) не могут иметь предельной точки, т. е. их можно расположить в порядке возрастания модулей. По теореме 5.1. построим целую функцию G₁ (s), имеющую своими нулями нули G(s). Полагая

Вапри s≠a_n,

видим, что φ(s) тАФ целая функция, нигде не равная нулю, т. е. и логарифм φ(s) тАФ целая функция. Но тогда φ(s) = e^H(s), где H(s) тАФ целая функция. Так же доказывается второе утверждение теоремы. Теорема доказана.

Теорема 5.3. Пусть G(s)тАФ целая функция конечного порядка α и G(0)≠0, s_n тАФ последовательность всех нулей G(s), причем 0 < |s₁| ≤ |s₂| ≤ .. ≤|s_n|≤ .. Тогда последовательность s_n имеет конечный показатель сходимости β≤α,

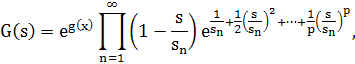
Где p≥0тАФ наименьшее целое число, для которого

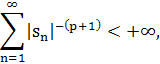
g(s)тАФ многочлен степени g ≤α и α = max (g, β) Если, кроме того, для любого с > 0 найдется бесконечная последовательность r₁, r₂, .., r_n, .., r_nВа+∞, такая, что

max |G(s)|>, |s| = r_n , n = 1, 2, тАж,

то α=β и рядВарасходится.

5.2 О бесконечности целых нетривиальных нулей L-функции Дирихле

Из следствия к теореме 4.1 видно, что функция L(s, χ), χ тАФ примитивный характер, имеет в полуплоскости Re s < 0 лишь действительные нули; эти нули являются полюсами Ваили Ваназываются тривиальными; тривиальным также называется нуль s = 0. Кроме тривиальных функция L(s, χ) имеет подобно дзета-функции бесконечно много нетривиальных нулей, лежащих в полосе (критическая полоса) 0 ≤ Re s ≤ 1.

Теорема 5.1. Пусть χ тАФ примитивный характер. Тогда функция ξ(s, χ) является целой функцией первого порядка, имеющей бесконечно много нулей ρ_n таких, что 0≤Re ρ_n ≤ 1, ρ_n ≠0, причем ряд расходится, а ряд

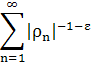
сходится при любом ε > 0. Нули ξ(s, χ) являются нетривиальными нулями L(s, χ).

Доказательство. При Re ≥1/2

Последняя оценка |ξ(s, χ)| в силу функционального уравнения (9) из Вз4 и равенства

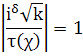
справедлива также при Re s +∞, по теореме 5.3 получаем первое утверждение теоремы. Так как L(s, χ)≠0 при Re s>l, то из

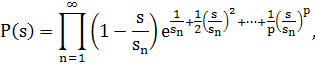
следует, что ξ(s, χ) ≠0 при Re s < 0, т. о. нули ξ(s, χ) являются нетривиальными нулями L(s, χ),лежащими в полосе 0≤Re s≤l. Теорема доказана.

Вз6. Обобщенная гипотеза Римана

Функция ζ(s) определена для всех комплексных s≠1 , и имеет нули для отрицательных целых s = тАФ2, тАФ4, тАФ6 .. Из функционального уравнения

,

и явного выражения

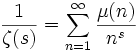
при Re s >1 следует, что все остальные нули, т.е. нетривиальные, расположены в полосе 0≤Re s ≤ 1 симметрично относительно критической линии . Гипотеза Римана утверждает, что:

Все нетривиальные нули дзета-функции имеют действительную часть, равную .

Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, то есть L-функций Дирихле

Библиографический список

1. А.Л. Карацуба, Основы аналитической теории чисел // 2-е над.тАФ М.: Наука. Главная редакция физико-математической литературы, 1983. -240 с.

2. С.М. Воронин, А.А. Карацуба, Дзета-функция Римана // М.: Физматлит. 1994. -376с.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Арифметичнi застосування теорii конгруенцiй

Волоконно-оптические датчики температуры на основе решеток показателя преломления