Надiйнiсть електронних апаратiв

Надiйнiсть електронних апаратiв

Содержание

1. Безвiдмовнiсть неремонтованих пристроiв

2. Безвiдмовнiсть ремонтованих ЕПА

3. Закони розподiлу часу безвiдмовноi роботи

3.1 Розподiл Вейбулла

3.2 Експоненцiальний розподiл

3.3 Розподiл Релея

3.4 Закон нормального розподiлу

3.5 Розподiл Пуассона

4. Ремонтопридатнiсть ЕА

5. Довговiчнiсть ЕА

6. Здатнiсть до зберiгання ЕА

7. Готовнiсть

1. Безвiдмовнiсть неремонтованих пристроiв

Надiйнiсть маi комплексну властивiсть. У залежностi вiд призначення ЕА та умов ii експлуатацii надiйнiсть може включати в себе безвiдмовнiсть, ремонтопридатнiсть, довговiчнiсть i здатнiсть до зберiгання. Зупинимося на цих властивостях апаратури бiльш детально.

Поняття безвiдмовностi i одним з важливiших у теорii надiйностi. Пiд безвiдмовнiстю розумiiться властивiсть апаратури безперервно зберiгати працездатнiсть протягом деякого часу або деякого напрацювання.

Основною кiлькiсною мiрою i ймовiрнiсть безвiдмовноi роботи P (t) - ймовiрнiсть того, що в межах заданого напрацювання вiдмова апарата не виникне.

тАЮНапрацювання" - термiн, який визначаi довготривалiсть роботи апаратури. Виникнення вiдмови i випадковою подiiю, а тому час появи вiдмови t₀ - також випадкова величина (t₀₁, t₀₂, тАж, t_0n).

Позначимо через t₀ - час справноi роботи апарата. Якщо взяти будь-який довiльно вибраний елемент, то заздалегiдь неможливо сказати, скiльки часу вiн пропрацюi до вiдмови, але можна визначити ймовiрнiсть того, що вiн не вiдмовить за деякий iнтервал часу t₀. Тодi ймовiрнiсть безвiдмовноi роботи можна представити як ймовiрнiсть того, що час безвiдмовноi роботи t₀ апаратури бiльше деякого заданого часу.

Звичайно, що чим бiльше заданий промiжок часу, для якого визначаiться надiйнiсть, тим менше значення безвiдмовноi роботи i навпаки. Практично величина ймовiрностi безвiдмовноi роботи визначаiться статистичним шляхом за iнформацiiю про вiдмови за вибраний промiжок часу:

Ва(1)

де N - кiлькiсть приладiв на початку випробовувань;

n_i - кiлькiсть приладiв, якi вiдмовити за час t_i.

При значнiй кiлькостi приладiв статистична ймовiрнiсть Ванаближаiться до ймовiрностi P (t).

Надiйнiсть обтАЩiкта iнколи зручнiше характеризувати ймовiрнiстю вiдмови:

Ва(2)

Таким чином, ймовiрнiсть появи вiдмови q (t) можна розглядати як ймовiрнiсть того, що випадкова величина t₀ набуде значення менше часу t, який розглядаiться. Це дозволяi розглядати q (t) як функцiю розподiлу випадковоi величини t₀ - часу до появи вiдмови.

Наведемо функцiональнi залежностi ймовiрностей безвiдмовноi роботи та вiдмови.

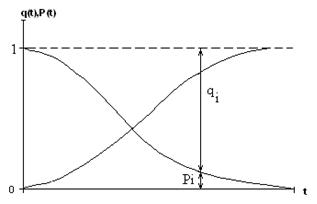
Рисунок 1 - Функцiональна залежнiсть P (t) та q (t)

Розглянемо бiльш докладно безвiдмовнiсть неремонтованих елементiв. Показниками безвiдмовностi неремонтованих елементiв i: ймовiрнiсть безвiдмовноi роботи P (t), частота вiдмов f (t), iнтенсивнiсть вiдмов λ (t) та середнi напрацювання до першоi вiдмови Т_ср.

Пiд частотою вiдмов елементiв (обтАЩiктiв) розумiють кiлькiсть вiдмов в одиницю часу, вiднесену до початковоi кiлькостi поставлених на випробовування елементiв. За статистичними даними частота вiдмов:

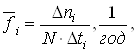Ва(3)

де Δn_i - кiлькiсть вiдмов за iнтервал часу Δt_i; N - кiлькiсть поставлених на випробування елементiв; Δt_i - час випробовувань.

При цьому елементи, якi вiдмовили у процесi випробовування, не замiнюються новими i кiлькiсть працюючих елементiв поступово зменшуiться.

Функцiю частоти вiдмов можна записати у такому виглядi:

Ва(4)

При Δt→0 ймовiрнiсть вiдмови за час вiд 0 до t може бути визначена iнтегруванням функцii f (t) у цьому ж iнтервалi:

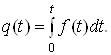
Тодi за час t ймовiрнiсть безвiдмовноi роботи:

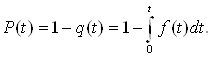Ва(5)

Щоб отримати залежнiсть мiж P (t) та f (t) у бiльш наочному виглядi, слiд продиференцiювати попереднi рiвняння (5). Отримуiмо:

Ваабо Ва(6)

Таким чином, функцiя частоти вiдмов f (t) i похiдна вiд функцii ймовiрностi безвiдмовноi роботи P (t), яка береться зi зворотним знаком. Вона характеризуi швидкiсть зменшення надiйностi у часi.

Оскiльки Вато замiнивши у рiвняннi (6) - P′ (t) на q′ (t), отримаiмо частоту вiдмов:

Ва(7)

Але q (t) i iнтегральний закон розподiлу часу безвiдмовноi роботи t₀, похiдна вiд якого являi собою щiльнiсть розподiлу ймовiрностi випадковоi величини t₀. Отже, функцiя частоти вiдмов f (t) - це щiльнiсть розподiлу часу безвiдмовноi роботи, тобто диференцiальний закон розподiлу випадковоi величини t₀.

Отриманi формули (5), (6) та (7) визначають взаiмодii P (t),q (t) i f (t).

Для системи, яка складаiться з ряду послiдовно зтАЩiднаних елементiв, ймовiрнiсть безвiдмовноi роботи можна показати у виглядi добутку ймовiрностей безвiдмовноi роботи всiх елементiв:

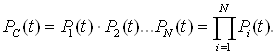Ва(8)

Критерiiм, який найбiльш повно характеризуi надiйнiсть неремонтованих обтАЩiктiв, i iнтенсивнiсть вiдмов. На вiдмiну вiд частоти вiдмов f (t), iнтенсивнiсть вiдмов характеризуi надiйнiсть обтАЩiкта у кожен даний момент, тобто його локальну надiйнiсть. Пiд iнтенсивнiстю вiдмов слiд розумiти кiлькiсть вiдмов в одиницю часу, вiднесену до середньоi кiлькостi елементiв, безвiдмовно працюючих у даний промiжок часу. При цьому елементи, якi вiдмовили, не замiнюються новими.

З експериментальних даних ця характеристика знаходиться за формулою:

Ва(9)

де Δn_i - кiлькiсть вiдмов за промiжок часу Δt_i;

N_cp= (N_i=N_i+1) /2 - середня кiлькiсть працездатних елементiв;

N_i - кiлькiсть елементiв, працездатних на початку даного промiжку часу;

N_i+1 - кiлькiсть елементiв, працездатних у кiнцi промiжку часу Δt_i.

РЖнтенсивнiсть вiдмов λ (t) повтАЩязана однозначною залежнiстю з частотою вiдмов f (t) та ймовiрнiстю безвiдмовноi роботи приладiв P (t). Для того, щоб знайти цю залежнiсть, змiнимо формулу (9), роздiливши чисельник i знаменник на NВ·Δt, та, скориставшись спiввiдношеннями (1) i (3), отримаiмо:

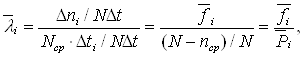Ва(10)

де N - кiлькiсть елементiв на початку експерименту;

n_cp - середня кiлькiсть елементiв, якi вiдмовили за час Δt_i.

Якщо перейти вiд дискретного поняття до безперервного, з урахуванням формули (6), отримаiмо:

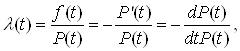
або пiсля диференцiювання:

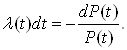
РозвтАЩязання цього диференцiального рiвняння вiдносно P (t) маi вигляд:

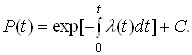Ва(11)

Значення постiйноi С знайдемо, скориставшись початковими умовами t=0 i P (0) =1, отже C=0.

Таким чином, остаточне розвтАЩязання диференцiального рiвняння (11) маi вигляд:

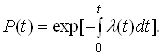Ва(12)

Якщо апаратура мiстить N послiдовно включених однотипних елементiв, то iнтенсивнiсть запишеться:

Ва(13)

За наявностi К груп рiзних елементiв в апаратурi отримаiмо суму:

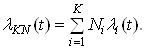Ва(14)

Залежнiсть iнтенсивностi вiдмов вiд часу експлуатацii для складноi апаратури маi вигляд:

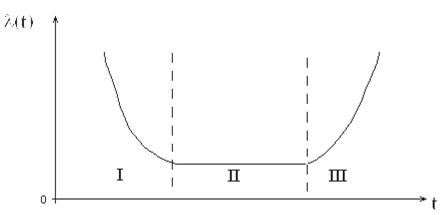
РЖ - область приробiтку; РЖРЖ - нормальна експлуатацiя; РЖРЖРЖ - область старiння

Рисунок 2 - Залежнiсть iнтенсивностi вiдмов вiд часу експлуатацii

Останнiй показник - середнi напрацювання до першоi вiдмови Т_ср.

Середнiм напрацювання до першоi вiдмови Т_ср називаiться математичне сподiвання роботи до першоi вiдмови.

Середнiй час безвiдмовноi роботи можна звтАЩязати аналiтичною залежнiстю з P (t), якщо скористаiмося вiдомим з теорii ймовiрностi спiввiдношенням мiж математичним сподiванням випадковоi величини та диференцiальним законом ii розподiлу:

Ва(0≤ х< ∞).

Але через те, що час безвiдмовноi роботи не може мати вiдтАЩiмних значень, проведемо iнтегрування для середнього напрацювання Т_ср вiд 0 до ∞. Тодi з урахуванням формули (6) маiмо:

Ва(15)

Зробимо iнтегрування отриманоi формули за частинами:

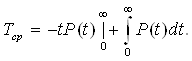
Очевидно, що у звтАЩязку з тим, що при верхнiй границi P (t) швидше наближаiться до нуля, нiж t 4 . Тодi середнi напрацювання до першоi вiдмови можна знайти за формулою:

Ва(16)

За даними експерименту Т_ср однотипних елементiв визначаiться як:

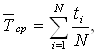
де t_i - час справноi роботи i-го елемента;

N - загальна кiлькiсть елементiв в експериментi.

Практично ж знати час довготривалостi справноi роботи t_i всiх елементiв неможливо.

Тодi:

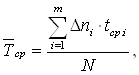Ва(17)

де Δп_i - кiлькiсть елементiв, якi вiдмовили за iнтервал часу Δt= (t_i+1-t_i);

t_i - час на початку i-го iнтервалу; t_i+1 - час в кiнцi i-го iнтервалу. При цьому t_{ср. i}= (t_i+t_i+1) /2; m= t_N /Δt - кiлькiсть елементiв, що вiдмовили за iнтервал Δt; t_N - час, протягом якого вiдмовили всi елементи.

Отриманий показник середнього напрацювання до першоi вiдмови найбiльш зручний для оцiнки надiйностi неремонтованих (не вiдновлювальних) елементiв.

надiйнiсть електронний апарат безвiдмовний

2. Безвiдмовнiсть ремонтованих ЕПА

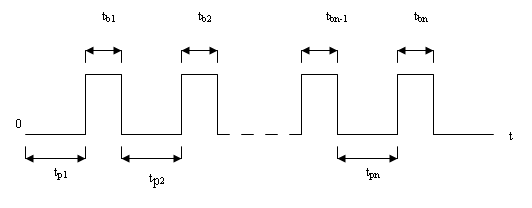Для ремонтованих апаратiв характерне чергування справного стану та ремонту пiсля вiдмови, тобто процес ii експлуатацii можна подати (показати) як послiдовнiсть чергування iнтервалiв часу працездатного i непрацездатного стану.

Рисунок 3 - Процес експлуатацii ремонтованого обтАЩiкта

Появу вiдмов у кожному з N обтАЩiктiв можна розглядати як потiк вимог до ремонту. Показниками безвiдмовностi ремонтованих обтАЩiктiв i: ймовiрнiсть безвiдмовноi роботи P (t), параметр потоку вiдмов ω (t), середнi напрацювання на вiдмову. Параметр потоку вiдмов (середня кiлькiсть вiдмов за час потоку, який розглядаiться) це:

Ва(18)

де N - кiлькiсть обтАЩiктiв, поставлених на випробування.

При цьому кiлькiсть обтАЩiктiв (апаратiв) у процесi випробування (експерименту) залишаiться незмiнною, тобто обтАЩiкти, якi вiдмовили, замiнюються новими. Умови замiни обтАЩiктiв, якi вiдмовили пiд час випробовування, вiдображають реальний процес експлуатацii, коли замiсть обтАЩiктiв (елементiв), якi вiдмовили, ставлять новi. У складних пристроях пiдсумковий потiк вiдмов дорiвнюi сумi потокiв вiдмов окремих пристроiв:

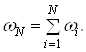Ва(19)

Основним типом потоку вiдмов ЕА в умовах експлуатацii i найпростiший, тобто потiк, який задовольняi умовам ординарностi, стацiонарностi та вiдсутностi пiслядii.

Для ремонтованих апаратiв зручним для практики критерiiм надiйностi i середня кiлькiсть годин роботи мiж двома сусiднiми вiдмовами, зазвичай ii називають напрацюванням на вiдмову .

Значення розглянутих показникiв можуть бути знайденi за результатами обробки статистичного матерiалу, отриманого пiд час експлуатацii або спецiально проведених експериментiв з групою однотипних приладiв. Таким чином, якщо апаратура визначеного типу пропрацювала сумарний час t_Σ та при цьому мала п вiдмов, то напрацювання на вiдмову:

Ва(20)

Якщо випробовуванням пiдлягають N однотипних обтАЩiктiв, то необхiдно знайти сумарний час справноi роботи всiх обтАЩiктiв та роздiлити його на загальну кiлькiсть вiдмов:

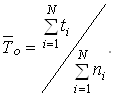Ва(21)

Для найпростiшого потоку параметр потоку вiдмов:

Ва(22)

3. Закони розподiлу часу безвiдмовноi роботи

Через те, що процес виникнення вiдмов ЕА маi випадковий характер та залежить вiд багатьох факторiв, отже, i час безвiдмовноi роботи i величина випадкова, для опису ii розподiлу в теорii надiйностi використовують ряд законiв. Найбiльше розповсюдження отримали закони: Вейбулла, експоненцiальний, Релея, нормальний, Пуассона тощо.

3.1 Розподiл Вейбулла

Згiдно з цим розподiлом, iмовiрнiсть безвiдмовноi роботи в iнтервалi 0, t запишеться:

Ва(23)

де - параметр розподiлу.

Звiдси функцiя частоти вiдмов:

Ва(24)

а середнiй час безвiдмовноi роботи:

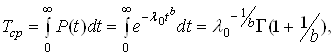Ва(25)

де табульована повна гамма-функцiя.

Цьому закону достатньо добре пiдпорядковуiться розподiл вiдмов в апаратурi, яка маi велику кiлькiсть однотипних неремонтованих елементiв (резистори, напiвпровiдниковi прилади тощо).

З вищенаведених залежностей ймовiрностi безвiдмовноi роботи та частоти вiдмов знаходимо iнтенсивнiсть вiдмов:

Ва(26)

Наведемо залежностi функцiй, якi побудованi за формулами (23); (24) та (26) для випадкiв, коли параметр розподiлу >1 i <1:

Рисунок 4 - Залежнiсть Р (t),λ (t) та f (t) при розподiлi часу безвiдмовноi роботи за законом Вейбулла: - - - <1; >1

3.2 Експоненцiальний розподiл

Цей розподiл можна розглядати як окремий випадок розподiлу Вейбулла при =1. Тодi, скориставшись формулами розподiлу Вейбулла, запишемо: частота вiдмов:

Ва(27)

ймовiрнiсть безвiдмовноi роботи:

Ва(28)

iнтенсивнiсть вiдмов:

Ва(29)

напрацювання до першоi вiдмови:

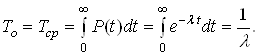
Пiдставивши в формулу ймовiрностi безвiдмовноi роботи значення iнтенсивностi вiдмов λ=1/Т_о, отримаiмо:

При t=T_o отримаiмо

При експлуатацiйному розподiлi математичне сподiвання випадковоi величини дорiвнюi середньоквадратичному вiдхиленню, тобто:

Експоненцiальний розподiл типовий для бiльшостi складних апаратiв, якi мiстять велику кiлькiсть неремонтованих елементiв та мають здебiльшого раптовi вiдмови. Експоненцiальний розподiл застосовують також до апаратiв, якi вiдновлюються, з найпростiшим потоком вiдмов. Наведемо залежностi Р (t),λ (t) та f (t) при розподiлi часу безвiдмовноi роботи за експоненцiальним законом:

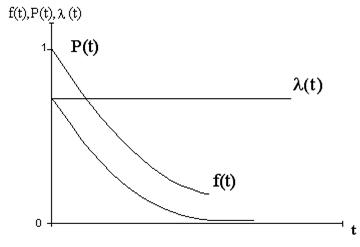
Рисунок 5 - Залежностi Р (t),λ (t) та f (t) при розподiлi часу безвiдмовноi роботи за експоненцiальним законом

3.3 Розподiл Релея

Цей розподiл достатньо повно описуi поведiнку ряду приладiв та елементiв ЕА з явно виявленим ефектом старiння та зносу. Ймовiрнiсть безвiдмовноi роботи записуiться при цьому у виглядi:

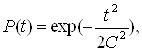Ва(30)

де С - параметр закону розподiлу.

Щiльнiсть ймовiрностi моменту вiдмови при цьому записуiться у такому виглядi:

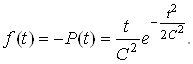Ва(31)

РЖнтенсивнiсть вiдмов:

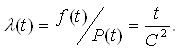Ва(32)

Середнi напрацювання на вiдмову:

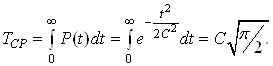Ва(33)

Залежностi Р (t),λ (t) та f (t) при розподiлi часу безвiдмовноi роботи за законом Релея наведенi на рис.6:

Рисунок 6 - Залежнiсть Р (t),λ (t) та f (t) при розподiлi часу безвiдмовноi роботи за законом Релея

3.4 Закон нормального розподiлу

Цей розподiл широко використовуiться в теорii ймовiрностi, а також i в теорii надiйностi. Даний закон описуi надiйнiсть апаратiв, для яких типовий знос, при цьому всi вiдмови однорiднi за якiстю та мають малий розкид зносу. Час ремонту апаратури, а також сумарне напрацювання апарата до ремонту iнколи також мають бути описанi нормальним законом розподiлу.

Щiльнiсть ймовiрностi моменту вiдмови у цьому випадку маi такий вигляд:

Ва(34)

Щiльнiсть залежить вiд двох параметрiв: середнього напрацювання на вiдмову та дисперсii σ_Т² часу безвiдмовноi роботи. Безпосередньо нормальний закон розподiлу для розрахунку показникiв безвiдмовностi може застосовуватися тiльки у випадку, коли середнi напрацювання до вiдмови:

Це повтАЩязано з тим, що нормальна щiльнiсть розподiлу не i односторонньою, тобто вона вiдрiзняiться вiд нуля i при t<0. При Т_СР>>0 цей недолiк практично не виявляiться, оскiльки в цьому випадку частиною кривоi розподiлу при t<0 можна знехтувати.

Проте, якщо умова Ване виконуiться, то використання нормального розподiлу може привести до помiтних похибок.

Тому на практицi використовують зрiзаний нормальний розподiл.

Для цього розрiзають частину кривоi розподiлу при t<0 та вводять нормований множник С_Н для зберiгання умови нормування щiльностi ймовiрностi:

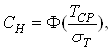Ва(35)

де 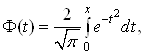Ва- функцiя Лапласа.

Тодi при зрiзаному нормальному розподiлi (t≥0) щiльнiсть ймовiрностi моменту вiдмови:

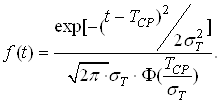Ва(36)

Ймовiрнiсть безвiдмовноi роботи:

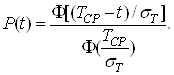Ва(37)

РЖнтенсивнiсть вiдмов:

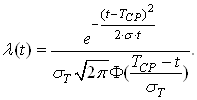Ва(38)

Середнi напрацювання до першоi вiдмови при зрiзаному нормальному розподiлi запишеться:

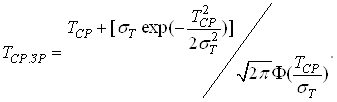Ва(39)

Залежнiсть Р (t),λ (t) та f (t) для нормального розподiлу часу безвiдмовноi роботи наведено на рис.7.

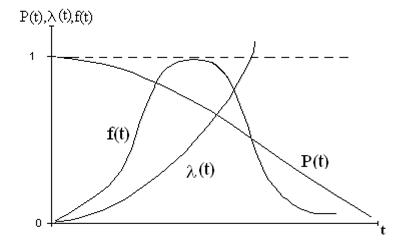
Рисунок 7 - Залежнiсть Р (t),λ (t) та f (t) при нормальному розподiлi часу безвiдмовноi роботи

3.5 Розподiл Пуассона

У теорii надiйностi широко використовуiться розподiл Пуассона, яким описують поведiнку дискретних випадкових величин. Вважаiться, що випадкова величина t розподiлена за законом Пуассона, якщо ймовiрнiсть того, що вона прийме означене значення К виражаiться формулою:

Ва(40)

де а - параметр закону Пуассона (математичне сподiвання випадковоi величини t).

Дисперсiя випадковоi величини t, розподiленоi за законом Пуассона, дорiвнюi ii математичному сподiванню:

Ва(41)

РЖнтервали часу мiж вiдмовами в пуассонiвському потоцi вiдмов взаiмоповтАЩязанi та розподiленi за експоненцiальним законом. Середня кiлькiсть вiдмов за iнтервал (0, t) для пуассонiвського потоку:

Ва(42)

Вигляд розподiлу Пуассона при рiзних значеннях математичного сподiвання а наведено на рис.8.

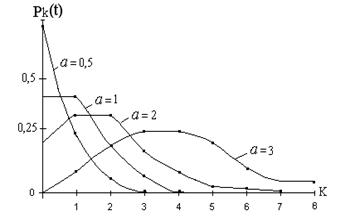
Рисунок 8 - Вигляд розподiл Пуассона при рiзних значеннях величини а

РЖнтенсивнiсть пуассонiвського потоку вiдмов:

тобто збiгаються з параметром експоненцiального розподiлу.

Розподiл Пуассона застосовуiться для оцiнки надiйностi ремонтованих апаратiв з найпростiшим потоком вiдмов.

4. Ремонтопридатнiсть ЕА

Показники ремонтопридатностi запроваджуються тiльки для ремонтованих апаратiв. Процес ремонту, який полягаi у виявленнi та усуненнi вiдмови, i випадковим. Як випадкова величина береться середнiй час ремонту, який складаiться з часу на виявлення вiдмови, часу на пошук причини та усунення наслiдкiв вiдмови.

Для кiлькiсноi оцiнки ремонтопридатностi вживаються два показники:

середня тривалiсть поточного ремонту ;

середня тривалiсть поточного обслуговування Т_{П. О}.

Розглянемо показник середньоi тривалостi поточного ремонту. Середня тривалiсть поточного ремонту i математичне сподiвання часу поновлення працездатностi:

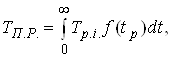Ва(43)

де Ва- час ремонту i - го апарата;

f (t_p) - щiльнiсть розподiлу випадковоi величини часу ремонту.

В процесi експлуатацii проводиться облiк вiдмов та час iх ремонту. Тодi за визначений час t за статистичними даними тривалiсть поточного ремонту:

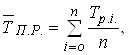Ва(44)

де п - кiлькiсть вiдмов за час t.

Величина, зворотня середнiй тривалостi поточного ремонту Ваназиваiться iнтенсивнiстю ремонту i характеризуi кiлькiсть ремонтiв, проведених за одиницю часу.

5. Довговiчнiсть ЕА

Пiд довговiчнiстю слiд розумiти властивiсть апарата зберiгати працездатнiсть до настання граничного стану за встановленою системою технiчного обслуговування i ремонту. На вiдмiну вiд визначення безвiдмовностi (де головним i безперервнiсть збереження працездатностi), визначення довговiчностi повтАЩязано iз збереженням працездатностi до заданоi межi з необхiдними перервами.

Для кiлькiсноi оцiнки властивостi апаратiв, якi обтАЩiднанi поняттям тАЮдовговiчностiтАЭ, використовують одиничнi показники довговiчностi: термiн служби та ресурс. Цi показники зазначаються в експлуатацiйнiй документацii (паспорт, формуляр тощо) i i основою для списування апаратури або вiдправки ii в середнiй або капiтальний ремонт.

Термiн служби визначаiться календарною тривалiстю експлуатацii або ii поновленнi пiсля середнього (капiтального) ремонту до граничного стану.

Для ремонтованих та неремонтованих приладiв розрiзняють: середнiй термiн служби, середнiй термiн служби до списування та гамма-вiдсотковий термiн служби.

Середнiй термiн служби - це математичне сподiвання термiну служби вiд початку експлуатацii до настання граничного стану:

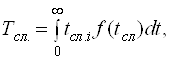Ва(45)

де Т_{сл. i. -} термiн служби i-го апарата;

f (t_сл.) - функцiя щiльностi розподiлу часу термiну служби.

За статистичними даними:

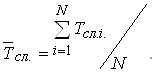Ва(46)

де Т_{сл. i. -} термiн служби i-го апарата;

N - кiлькiсть апаратiв.

Середнiй термiн служби до списування визначаiться часом вiд початку експлуатацii ЕА до ii списування, зумовленого граничним станом:

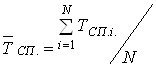. (47)

Гамма-вiдсотковий термiн служби Т_{сл. γ} - термiн служби, протягом якого апаратура не досягла граничного стану iз заданою ймовiрнiстю γ - вiдсоткiв. Наприклад, при γ=95% (95% -й термiн служби) 95% апаратiв даноi партii не досягають граничного стану за встановлений термiн служби. Гамма-вiдсотковий термiн служби визначаiться виразом:

Ва(48)

де q (Т_{сл. γ}) - функцiя розподiлу термiну служби.

Стосовно ремонтованоi апаратури розпiзнають додатково середнiй термiн служби до середнього (капiтального) ремонту. Середнiй термiн служби до середнього (капiтального) ремонту Т_{сл. ср. (}Т_{сл. к}) - середнiй термiн служби вiд початку експлуатацii до його першого середнього (капiтального) ремонту.

Середнiй термiн служби мiж середнiми (капiтальними) ремонтами Т_{сл. м. ср. (}Т_{сл. м. к.)} - середнiй термiн служби мiж сумiжними середнiми (капiтальними) ремонтами.

Гарантiйним термiном служби називаiться час, протягом якого виявляються дефекти, якi невиявленi при виготовленнi апаратури, а виробник за умови дотримання споживачем правил експлуатацii апаратури, в тому числi правил зберiгання i транспортування, забезпечуi виконання встановлених вимог до апаратури i несе вiдповiдальнiсть.

Ресурсом називають напрацювання апаратури вiд початку експлуатацii або його вiдновлення пiсля середнього або капiтального ремонту до настання граничного стану. Для апаратури розрiзняють середнiй ресурс, призначений ресурс i гамма-вiдсотковий ресурс.

Середнiй ресурс R_{ср -} математичне сподiвання ресурсу:

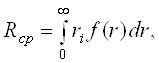Ва(49)

де r_i - ресурс роботи i-го елемента (апарата);

f (r) - функцiя щiльностi розподiлу величини r.

Призначений ресурс R_н - сумарне напрацювання апарата, при досягненнi якого експлуатацiя маi бути припинена незалежно вiд його стану.

Гамма-вiдсотковий ресурс R_{γ -} напрацювання, протягом якого апарат не досягаi граничного стану з заданою ймовiрнiстю γ - вiдсоткiв.

Для ремонтованих апаратiв розрiзняють середнiй ресурс до середнього (капiтального) ремонту R_ср (R_к), середнiй ресурс мiж ремонтами R_{м. ср. (}R_{ср. к.)}, середнiй ресурс до списання R_СП.

Середнiй ресурс до середнього (капiтального) ремонту - це середнiй час вiд початку експлуатацii апарата до його першого середнього (капiтального) ремонту. Середнiй ресурс мiж середнiми (капiтальними) ремонтами - це середнiй час мiж сумiжними ремонтами. Середнiй ресурс до списання - це середнiй час вiд початку експлуатацii до списання апаратури при граничному станi.

6. Здатнiсть до зберiгання ЕА

Неабияким, особливо для апаратiв з тривалими термiнами зберiгання, i властивiсть апарата зберiгати на етапах зберiгання та транспортування своi заданi експлуатацiйнi властивостi. У процесi експлуатацii в елементах апаратури вiдбуваються природнi фiзико-хiмiчнi процеси, якi викликають iх старiння. Крiм того, на апаратуру впливають рiзнi фактори зовнiшнього середовища, якi прискорюють процес старiння елементiв.

Все це призводить до змiни властивостей, а також i параметрiв комплектуючих елементiв, що в остаточному пiдсумку приводить до змiни технiчних та експлуатацiйних характеристик апаратури. При значнiй змiнi параметрiв елементiв цi характеристики можуть вийти за межi експлуатацiйних припускiв та призвести до вiдмови апаратури.

Як одиночнi показники, якi дозволяють кiлькiсно визначити здатнiсть до збереження, використовують середнiй термiн збереження та гамма-вiдсотковий термiн збереження.

Середнiй термiн збереження - це математичне сподiвання термiну зберiгання:

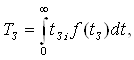Ва(50)

де t_Зi - термiн зберiгання i-го апарата;

f (t_З) - щiльнiсть розподiлу величини.

За статистичними даними середнiй термiн зберiгання:

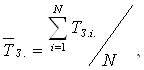Ва(51)

де N - кiлькiсть апаратiв;

T_Зi - термiн зберiгання i-го апарата.

Гамма-вiдсотковий термiн зберiгання Т_Зγ - це термiн, протягом якого апарат залишаiться працездатним iз заданою ймовiрнiстю γ - вiдсоткiв.

Гамма-вiдсотковий термiн зберiгання визначаiться:

Ва(52)

де Вафункцiя розподiлу термiну зберiгання.

7. Готовнiсть

Готовнiсть i важливим поняттям, яке застосовуiться не тiльки до ЕА, а i до персоналу, який обслуговуi ii. Готовнiсть визначаiться такими основними властивостями та факторами:

надiйнiстю;

прийнятою системою технiчного обслуговування i контролю технiчного стану;

органiзацiiю процесу обслуговування заявок та iнтенсивнiстю iх надходження;

квалiфiкацiiю обслуговуючого персоналу.

Властивостi та фактори, якi визначають рiвень готовностi ЕА, за своiю природою i випадковими, оскiльки вони залежать вiд великоi кiлькостi випадкових характеристик i параметрiв (наявнiсть можливих вiдмов, характеру потрiбного ремонту, регулювань, технiчного стану апаратури до моменту перевiрки тощо). Отже, i показники готовностi ЕА носять ймовiрно-статистичний характер.

Показники готовностi називають ще комплексними показниками надiйностi, оскiльки вони характеризують одночасно декiлька властивостей, якi складають надiйнiсть. Показниками готовностi i: коефiцiiнт готовностi К_г, коефiцiiнт оперативноi готовностi К_{о. г.,} коефiцiiнт технiчного використання К_{т. в.}

Коефiцiiнт готовностi К_г - це ймовiрнiсть того, що апаратура буде працездатною в довiльний момент часу, окрiм планових перiодiв, протягом яких використання апаратури за призначенням не передбачене (планове технiчне обслуговування, плановий ремонт). Отже, коефiцiiнт готовностi К_г - це вiдношення сумарного часу справноi роботи до загального часу справноi роботи i ремонту, взятого за визначений перiод експлуатацii.

Для бiльшостi ремонтованих апаратiв маi мiсце такий порядок обслуговування, коли пiсля появи вiдмови передбачаiться негайне ii усунення. Тодi:

Ва(53)

З цiii формули видно, що величина коефiцiiнта готовностi К_г може бути пiдвищена як за рахунок збiльшення напрацювання на вiдмову Т_о, так i за рахунок скорочення середньоi тривалостi поточного ремонту Т_П.Р. Таким чином, К_г характеризуi одночасно двi рiзнi властивостi апаратури: ii безвiдмовнiсть та ремонтопридатнiсть. Коефiцiiнт оперативноi готовностi К_{о. г} - це ймовiрнiсть того, що апарат, який знаходиться в режимi очiкування, виявиться працездатним в довiльний момент часу i, починаючи з цього моменту, працюватиме безвiдмовно протягом заданого iнтервалу часу. Ми вже розглядали, що ймовiрнiсть знаходження апаратури у працездатному станi в довiльний момент часу характеризуiться коефiцiiнтом готовностi К_г, а ймовiрнiсть того, що апаратура залишиться працездатною протягом заданого часу t - ймовiрнiстю безвiдмовноi роботи. Тодi:

Ва(54)

Коефiцiiнт технiчного використання К_{т. в. -} це вiдношення математичного сподiвання часу перебування апарата у працездатному станi за деякий промiжок часу до суми математичних сподiвань часу перебування апарата у працездатному станi, часу простою, обумовленому технiчним обслуговуванням та часу ремонтiв за той самий перiод експлуатацii.

На основi статистичних даних, отриманих за перiод експлуатацii, який розглядаiться:

Ва(55)

де Т_ОΣ - сумарне напрацювання всiх апаратiв;

Т_{Р. Σ} - сумарний час простою через плановi та неплановi ремонти всiх приладiв;

Т_{Т.О. Σ} - сумарний час простою через плановi та неплановi технiчнi обслуговування всiх приладiв.

Вместе с этим смотрят:

IP-телефония. Особенности цифровой офисной связи

РЖсторiя звтАЩязку та його розвиток

Автоматика, телемеханика и связь

Анализ режимов автоматического управления

Аргоновый лазер