Комплексный анализ методов теории нечетких множеств

Наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Традиционные компьютерные вычисления Влслишком точныВ» для реального мира. Человечество столкнулось с проблемами, для решения которых невозможно получить полную информацию или определение которых недостаточно полно. Казалось бы ситуация безвыходная, но благодаря развитию и совершенствованию так называемых нечетких и гибридных систем в настоящее время уже довольно обыденно воспринимаются ВлинтеллектуальныеВ» стиральные машины и бытовые автоматы, гиперзвуковые самолеты и самонаводящиеся ракеты и многое другое.

Математическую основу нечетких и гибридных систем составляют противоположные традиционным компьютерным вычислениям (hard computing), так называемые мягкие вычисления (soft computing), одной из составляющих которых является нечеткая логика.

В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Именно это делает эту тему актуальной и интересной для изучения.

Цель данной работы тАУ изучение возможности применения нечеткой логики как инструмента для принятия решений. Предметом изучения работы является теория нечетких множеств. Объект изучения работы тАУ методы теории нечетких множеств, применяемые для решения различных задач.

Таким образом, задачи моей работы:

1) Дать теоретическое описание нечетких множеств;

2) Рассмотреть пример описания неопределенности с помощью нечеткого множества;

3) Сравнить практические методы принятия решений с помощью нечеткой логики;

5) Выявить преимущества данных методов на основе полученных результатов.

ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ НЕЧЕТКИХ МНОЖЕСТВ

1. Нечеткие множества

Пусть A - некоторое множество. Подмножество B множества A характеризуется своей характеристической функцией

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности ВаЗначение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х тАУ она одновременно и входит, и не входит в нечеткое множество С. За вхождение - 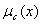Вашансов, за второе тАУ (1- 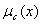) шансов.

Если функция принадлежности 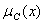Ваимеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A. Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества тАУ частный случай нечетких. Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.

Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.

Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности

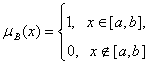
задает интервальную неопределенность тАУ про рассматриваемую величину известно лишь, что она лежит в заданном интервале [a,b]. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.

Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А.Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. Первая книга российского автора по теории нечеткости вышла в 1980 г. [1].

Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами.

Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.

Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть C и D- два нечетких подмножества A с функциями принадлежност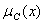и и 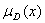соответственно. Пересечением 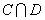, произведением CD, объединением , отрицанием 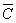, суммой C+D называются нечеткие подмножества A с функциями принадлежности

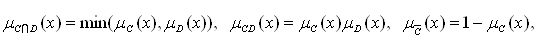
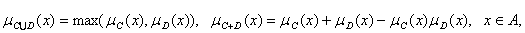
соответственно.

Как уже отмечалось, теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен ниже. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.

Для знакомства со спецификой нечетких множеств рассмотрим некоторые их свойства.

В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества Y.

2. Пример описания неопределенности с помощью нечеткого множества

Понятие ВлбогатыйВ» часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели в 1996 г. социологическое исследование представления различных слоёв населения о понятии "богатый человек".

Мини-анкета опроса выглядела так:

1. При каком месячном доходе (в млн. руб. на одного человека) Вы считали бы себя богатым человеком?

2. Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:

а) богатые;

б) достаток выше среднего;

в) достаток ниже среднего;

г) бедные;

д) за чертой бедности?

(В дальнейшем вместо полного наименования категорий будем оперировать буквами, например "в" - категория, "б" - категория и т.д.)

3. Ваша профессия, специальность.

Всего было опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл.1, а аналогичные сведения для работников коммерческой сферы тАУ в табл.2.

Таблица 1.

Типичные ответы научных работников и преподавателей

Ответы на вопрос 3	Ответы на вопрос 1, млн. руб./чел.	Ответы на вопрос 2	Пол
Кандидат наук	1	Д	ж
Преподаватель	1	В	ж
Доцент	1	б	ж
Учитель	10	в	м
Старший. научный сотрудник	10	д	м
Инженер-физик	24	д	ж
Программист	25	г	м
научный работник	45	г	м

Таблица 2

Типичные ответы работников коммерческой сферы.

Ответы на вопрос 3	Ответы на вопрос 1	Ответы на вопрос 2	Пол
Вице-президент банка	100	а	ж
Зам. директора банка	50	б	ж
Начальник. кредитного отдела	50	б	м
Начальник отдела ценных бумаг	10	б	м
Главный бухгалтер	20	д	ж
Бухгалтер	15	в	ж
Менеджер банка	11	б	м
Начальник отдела проектирования	10	в	ж

Вместе с этим смотрят:

РЖнформацiйний менеджмент як ефективна технологiя органiзацii управлiнськоi дiяльностi

Аксiологiчнi проблеми управлiнськоi дiяльностi робiтника освiти в умовах модернiзацii освiтньоi галузi в Украiнi

Американская система менеджмента на предприятии

Анализ ключевых компетенций для успеха в отрасли ООО "Галеон"

Анализ конкуренции в отрасли ресторанного бизнеса