Высшая математика
Федеральное агентство по образованию
ГОУ ВПО
Филиал Уральского государственного экономического университета
в г. Березники
Кафедра Влматематических и естественнонаучных дисциплинВ»
Контрольная работа
по дисциплине: Влвысшая математикаВ»
Тема: ВлВариант № 18В»
Выполнил:
студент I курса, группы ЭКПС-091
Лоскутова Ирина Петровна .
Проверил:
к. ф-м. н., профессор .
Кобзев Виктор Николаевич .
Березники
2010
Содержание
1. ВаВаВа Задача № 1
2.ВаВаВаВа Задача № 2
3.ВаВаВаВа Список литературы
Вариант № 18
№ 1
Составить оптимальный суточный рацион для откорма крупного рогатого скота, имеющий наименьшую стоимость. Рацион состоит из силоса и концентратов. Содержание каротина и кормовых ед. в 1 кг силоса 0 и 4 ед. соответственно, а в 1 кг концентратов 1 и 3 ед. соответственно. Для каждого животного суточная норма каротина 5 ед., а кормовых ед. 31. Цена 1 кг силоса 20 руб., а 1 кг. концентратов 30 руб.
а) Записать математическую модель задачи.
б) Решить задачу графическим методом.
а) Пусть Х1 и Х2 тАУ количество каротина и кормовых единиц, необходимых для откорма.
Тогда суточный рацион задается целевой функцией Z(Х)=20Х1+30Х2
Т.к. суточная норма ограничена, то Х1 и Х2 должны удовлетворять неравенствам 4Х2 ≥5
Х1+3Х2≥31
Х1≥0, Х2≥0
математический функция уравнение неизвестное
Таким образом, математическая модель имеет вид
Найти значения Х1 и Х2, удовлетворяющие системе неравенств
Ва4Х2≥5
ВаХ1+3Х2≥31
ВаХ1≥0, Х2≥0
и при которых функция Z(Х)=5Х1+31Х2 достигает минимума.
б) Решим задачу графическим методом.
1. построим прямые
Ва4Х2=5 Х1+3Х2=31
ВаХ2=1,25
2. Для каждой прямой выделим полуплоскость, соответствующую неравенству
- выбираем точку не принадлежащую прямым (например, т. (0;0))
- подставляем ее координаты в каждое неравенство
- если неравенство верное, то выделяем полуплоскость, в которой лежит данная точка.
- если неравенство не верное, то выделяем другую полуплоскость.
т. (0;0) 4*0=0<5 (в)
1*0+3*0=0<31 (в)
3. выделим общую часть полуплоскостей, получая ОДР задачи.
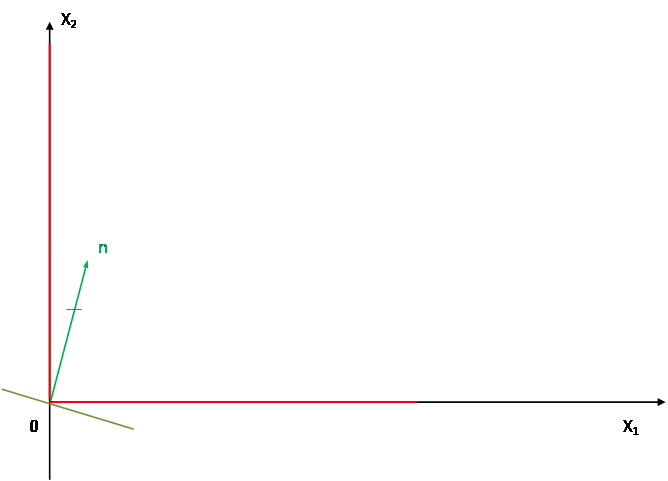
4. Сроим вектор n ={5;31} и прямую (линию уровня) Z=0 n
5. Продвигаем линию уровня Z=0 в направлении вектора n до тех пор, пока она не перестанет пересекать ОДР, т.е. пока не будут касаться этой области.
6. Найдем координаты т. С решив систему уравнений
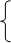
Ва4Х2=5 Х2=1,25 Х2=1,25
ВаХ1+3Х2=31 Х1=30 - 3Х2 Х1=27,25