Геометричнi мiсця точок на площинi та iх застосування

КУРСОВА РОБОТА

на тему:

ВлГеометричнi мiсця точок на площинi та iх застосуванняВ»

Вступ

Актуальнiсть дослiдження. Поняття геометричного мiсця точок у просторi (ГМТ) маi велике методичне i загальноосвiтнi значення. Неможливо переоцiнити його роль у розвитку просторовоi уяви.

Розв'язування задач, в яких застосовуються геометричнi мiсця точок як на площинi, так i в просторi, активiзують творчу думку i фантазiю, розвивають логiчне мислення, кмiтливiсть, змушують перебирати в пам'ятi всi вiдомi теореми з метою вiдбору i застосування найбiльш придатноi з них.

Таким чином, тема Геометричнi мiсця точок на площинi та iх застосування, на сучасному етапi i досить актуальною.

ЗвтАЩязок роботи з науковими планами, програмами, темами. Дана курсова робота повтАЩязана з дисциплiною Геометрiя та загальним навчальним планом Миколаiвського державного унiверситету iменi В.О. Сухомлинського.

ОбтАЩiкт дослiдження. Роздiл геометрii тАУ аналiтична геометрii та його застосування на практицi.

Предметом дослiдження i геометричнi мiсця точок на площинi та iх застосування.

Метою дослiдження i теоретичне та практичне застосування поняття геометрii тАУ геометричнi мiсця точок на площинi.

Вiдповiдно до поставленоi мети нам необхiдно вирiшити наступнi завдання:

1. Дослiдити наукову та методичну лiтературу з обраноi теми курсовоi роботи.

2. Здiйснити загальну характеристику визначення ГМТ в межах курсового дослiдження.

3. Проаналiзувати основнi ГМТ на площинi.

4. Привести приклади задач на вiдшукання ГМТ

5. Висвiтлити процес застосування ГМТ до розвтАЩязання задач на побудову.

Теоретичне та практичне значення. Матерiали даноi курсовоi роботи можна використовувати при викладаннi вiдповiдноi теми з курсу Геометрiя, а також для участi у наукових семiнарах та конференцiях, викладання на уроках геометрii.

1. Визначення ГМТ

Геометричне мiсце точок i одним з найважливiших понять геометрii. Але воно широко використовуiться не лише в геометрii, ай в математичному аналiзi, механiцi i в багатьох технiчних дисциплiнах. Тому поняття геометричного мiсця точок маi велике загальноосвiтнi значення.

Означення. Геометричним мiсцем точок називаiмо фiгуру, всi точки якоi мають певну властивiсть, яка належить обов'язково i виключно точкам цiii фiгури.

Коли розглядати геометричне мiсце точок на площинi, то можна одержати, наприклад: пряму, промiнь, коло i iншi плоскi кривi, точку, сукупнiсть iзольованих точок, сукупнiсть прямих, вiдрiзок, сукупнiсть вiдрiзкiв, дугу, сукупнiсть дуг, деяку частину площини тощо.

На поняттi про геометричне мiсце точок ТСрунтуiться особливий спосiб розв'язування задач на побудову, що маi назву методу геометричних мiсць. Суть його така: зводять всю задачу на побудову до вiдшукання положення на площинi однiii або декiлькох точок, якi визначаються двома умовами, що випливають з вимог задачi. Якщо вiдкинути одну з цих умов задачi, то вона стане невизначеною i решту умов буде задовольняти, не одна точка, а нескiнченна множина точок, що утворюють якесь геометричне мiсце. Якщо потiм вiдновити вiдкинуту умову, а вiдкинути другу, то решту умов, знов буде задовольняти нескiнченна множина точок, що утворюють нове геометричне мiсце. Кожна точка перетину цих двох геометричних мiсць задовольняi вимогам задачi i, отже, буде шуканою. Задача матиме стiльки розв'язкiв, скiльки спiльних точок мають знайденi геометричнi мiсця.

Подана характеристика методу геометричних мiсць показуi, що його застосовують при розв'язуваннi таких задач, умову яких можна розчленувати на двi незалежнi вимоги, кожна з яких окремо визначаi вiдповiдне геометричне мiсце точок. Правда, iнколи одно з геометричних мiсць буваi заданим самою умовою задачi.

Позитивними рисами методу i такi: а) при розв'язуваннi задач методом гeoметричних мiсць спрощуiться вiдшукання плану розв'язування задачi i способу ii побудови; б) вiдкидаючи одну умову задачi i змiнюючи iншу, можна об'iднати декiлька задач на побудову в одну групу i розглядати iх як рiзнi варiанти деякоi загальноi конструктивноi проблеми.

Пояснимо сказане про особливостi методу геометричних мiсць точок на такому прикладi:

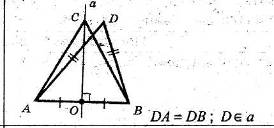
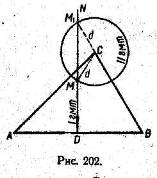
Задача. Дано трикутник ABC. Побудувати в площинi три кутника точку М, яка була б на однаковiй вiддалi вiд вершин А та В i на вiддалi d вiд третьоi вершини С (рис. 202).

Аналiз. Шукана точка М повинна задовольняти двi умови: а) вона повинна знаходитись на однаковiй вiддалi вiд двох точок А i В i б) вона повинна знаходитись на вiддалi d вiд третьоi точки.

Вiдкинемо другу умову. Тодi одну першу умову буде задовольняти нескiнченна множина точок, що утворюють геометричне мiсце тАУ перпендикуляр, проведений через середину D вiдрiзка АВ. Збережемо тепер другу умову i вiдкинемо першу. Тодi одну другу умову буде задовольняти нескiнченна множина точок, що утворюють геометричне мiсце тАУ коло з центром в точцi С i радiусом, рiвним d. Точки М i М₁ перетину першого геометричного мiсця з другим будуть Шуканими.ВаВаВа

Побудов а. Для розв'язування задачi потрiбно побудувати перше i друге геометричнi мiсця.

Будуiмо перпендикуляр ND до вiдрiзка АВ в його серединi D (основна побудова див. Вз 2) i коло радiусом, рiвним а, з цент ром в С; точка перетину кола з перпендикуляром ND визначить шукану точку M.

Дослiдження. Оскiльки коло може перетинати пряму не бiльш нiж в двох точках, то залежно вiд даних (∆ ABC i d) задача може не мати жодного розв'язку або мати до двох роз в'язкiв. На рис. 202 показано випадок двох розв'язкiв.

При розв'язуваннi задачi ми користувались першим i другим геометричним мiсцем, як даними. Ця обставина приводить до необхiдностi знання хоча б основних геометричних мiсць на площинi, якщо ми бажаiмо навчитись розв'язувати задачi на побудову методом геометричних мiсць.

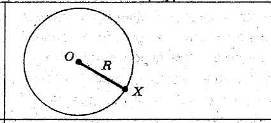
2. Основнi ГМТ на площинi

РЖ. Геометричним мiсцем точок, рiвновiддалених вiд даноi точки, i коло з центром у цiй точцi i з радiусом, який дорiвнюi данiй вiдстанi.
РЖРЖ. Геометричним мiсцем точок, рiвновiддалених вiд двох даних точок, i серединний перпендикуляр до вiдрiзка, який з'iднуi цi точки.
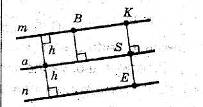
РЖРЖРЖ. Геометричне мiсце точок, вiддалених вiд даноi прямоi на вiдстань А, складаiться з двох прямих, паралельних данiй i вiддалених вiд неi на вiдстань h:
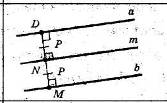
Геометричним мiсцем точок, рiвновiддалених вiд двох паралельних прямих, i пряма, паралельна даним прямим i однаково вiддалена вiд них.
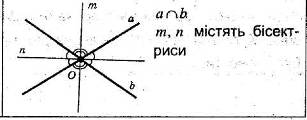
Геометричне мiсце точок, рiвновiддалених вiд двох прямих, що перетинаються, складаiться з двох прямих, якi мiстять бiсектриси кутiв, отриманих в результатi перетину даних прямих.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Волоконно-оптические датчики температуры на основе решеток показателя преломления

Время и пространство - идеалистические понятия