Уравнение Дирака в квантовой теории
1. Уравнение Дирака
2. Матрица Дирака. Свойства матриц Дирака
3. Спиноры
4. Общее решение уравнения Дирака
Заключение
Список литературы
Введение
Курсовая работа состоит из введения, четырех параграфов, заключения и списка с литературой.
В первом параграфе раскрывается понятие об уравнение Дирака и вводится обозначение матриц Дирака 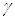 , записывается вид уравнения Дирака. Во втором параграфе рассматриваются основные свойства матриц Дирака. В третьем тАУ определяется понятие о спиноре. А в четвертом параграфе выводится решение уравнения Дирака в виде плоских волн.
, записывается вид уравнения Дирака. Во втором параграфе рассматриваются основные свойства матриц Дирака. В третьем тАУ определяется понятие о спиноре. А в четвертом параграфе выводится решение уравнения Дирака в виде плоских волн.
Кратко остановимся на релятивистских обозначениях, которые будут нами использоваться.
Пространственно-временные координаты будут обозначаться 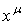 , причем
, причем 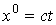 ,
, 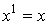 ,
, 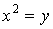 Ваи
Ваи 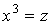 ;
;  . Мы будем использовать метрический тензор
. Мы будем использовать метрический тензор 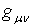 Вас компонентами
Вас компонентами
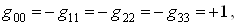
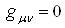 Вапри
Вапри 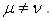
уравнение дирак матрица спинор
В связи с этим нужно различать ковариантные и контравариантные векторы. Контравариантный вектор (преобразующийся как координатный вектор 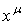 ) будет обозначаться
) будет обозначаться 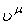 , а ковариантный (преобразующийся как градиент) будет обозначаться
, а ковариантный (преобразующийся как градиент) будет обозначаться 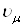 . Аналогичные обозначения будут приняты и для тензоров. Греческие индексы будут применяться для обозначения компонент (0, 1, 2, 3) пространственно-временного тензора, а латинские индексы тАУ только для обозначения пространственных компонент (1, 2, 3). Операции опускания и поднимания индексов с помощью метрического тензора определяются следующим образом:
. Аналогичные обозначения будут приняты и для тензоров. Греческие индексы будут применяться для обозначения компонент (0, 1, 2, 3) пространственно-временного тензора, а латинские индексы тАУ только для обозначения пространственных компонент (1, 2, 3). Операции опускания и поднимания индексов с помощью метрического тензора определяются следующим образом:
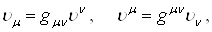
где предполагается суммирование от 0 до 3 по повторяющимся греческим индексам, т.е
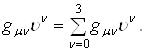
Тензор 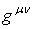 Ваопределяется уравнением
Ваопределяется уравнением 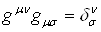 , где
, где 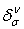 ВатАУ символ Кронекера:
ВатАУ символ Кронекера: 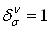 , если
, если 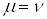 , и
, и 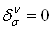 в противном случае.
в противном случае.
Введем в рассмотрение еще несколько понятий.
Транспонированным к  Ваназывают тензор
Ваназывают тензор  , который имеет в каком-либо базисе
, который имеет в каком-либо базисе  Ва"перевернутые" компоненты:
Ва"перевернутые" компоненты:
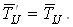
Транспонированный тензор обозначают как  .
.
Симметричным называют такой тензор, транспонированный к которому совпадает с исходным:

Тензор 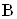 Ваназывают обратным к
Ваназывают обратным к  , если его скалярное произведение на
, если его скалярное произведение на  Вадает единичный тензор. Такой тензор
Вадает единичный тензор. Такой тензор 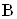 Ваобозначают как
Ваобозначают как  :
:

Ортогональным называют тензор  , обратный к которому тензор
, обратный к которому тензор  Васовпадает с транспонированным
Васовпадает с транспонированным  .
.
1. Уравнение Дирака
В начале XX века, пытаясь преодолеть трудности с отрицательными плотностями вероятности в уравнении Клейна-Гордона, которое выглядит следующим образом:
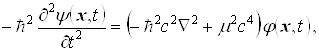 Ва(1.1)
Ва(1.1)
Дирак открыл релятивистское уравнение, которое теперь называют в его честь. Долгое время после открытия уравнения Дирака считали, что для частиц с массой это единственное правильное релятивистское волновое уравнение. И только после того, как Паули и Вайскопф дали новую интерпретацию уравнения Клейна-Гордона как уравнения для поля, это широко распространившееся мнение было опровергнуто. Но даже и теперь уравнение Дирака имеет особое значение, так как оно описывает частицы со спином 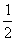 , а спин
, а спин 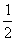 Ваимеют электроны и протоны (с понятием "спинор" познакомимся ниже). Многие другие "элементарные частицы" также обладают спином
Ваимеют электроны и протоны (с понятием "спинор" познакомимся ниже). Многие другие "элементарные частицы" также обладают спином 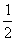 .
.
Соображения, которые привели Дирака к его уравнению, следующие. Для того, чтобы предотвратить появление отрицательных вероятностей, нужно, чтобы в выражении для плотности
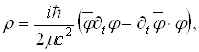 Ва(1.2)
Ва(1.2)
не было производных по времени. Поэтому волновое уравнение должно содержать производные по времени не выше первого порядка. Но релятивистская ковариантность требует полной симметрии по всем пространственным и временным координатам. Поэтому нужно, чтобы в волновое уравнение входили производные только первого порядка и по пространственным переменным. Таким образом, волновая функция Дирака должна удовлетворять линейному дифференциальному уравнению первого порядка по всем четырем координатам. Линейность уравнения нужна, чтобы удовлетворить принципу суперпозиции квантовой механики. Если мы хотим, чтобы волновая функция 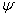 Ваописывала свободную частицу с массой m, то нужно потребовать, чтобы она подчинялась уравнению
Ваописывала свободную частицу с массой m, то нужно потребовать, чтобы она подчинялась уравнению
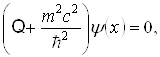 Ва(1.3)
Ва(1.3)
Где
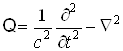
оператор Даламбера, так как уравнение означает, что между энергией и импульсом свободной частицы выполняется соотношение 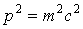 Ваи что в согласии с принципом соответствия имеется предельный переход к случаю классической теории относительности.
Ваи что в согласии с принципом соответствия имеется предельный переход к случаю классической теории относительности.
Аналогичная ситуация встречается и электродинамике, где уравнения Максвелла являются уравнениями первого порядка, связывающими компоненты напряженностей поля. В то же время каждая компонента электрической и магнитной напряженностей подчиняется волновому уравнению. Волновое уравнение в электродинамике является уравнением второго порядка, не содержащим массового члена, что свидетельствует о нулевой массе покоя фотона.
Предположим, что 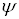 Ваимеет N компонент
Ваимеет N компонент 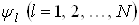 , причем мы заранее не фиксируем значение N. Наиболее общим линейным уравнением первого порядка является уравнение, выражающее временную производную одной компоненты в виде линейной комбинации всех компонент и их пространственных производных. Если подставить соответствующие размерные множители, то наиболее общее уравнение можно записать в виде
, причем мы заранее не фиксируем значение N. Наиболее общим линейным уравнением первого порядка является уравнение, выражающее временную производную одной компоненты в виде линейной комбинации всех компонент и их пространственных производных. Если подставить соответствующие размерные множители, то наиболее общее уравнение можно записать в виде
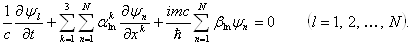 (1.4)
(1.4)
На основе предположения об однородности пространства-времени 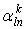 Ваи
Ваи 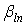 Ваявляются безразмерными константами, не зависящими от пространственно-временных координат
Ваявляются безразмерными константами, не зависящими от пространственно-временных координат 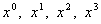 . Естественный способ упрощения вида этих уравнений состоит в использовании матричной записи, которая позволяет представить систему уравнений (1.4) в виде
. Естественный способ упрощения вида этих уравнений состоит в использовании матричной записи, которая позволяет представить систему уравнений (1.4) в виде
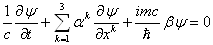 Ва(1.5)
Ва(1.5)
В этом уравнении 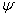 Ваесть матрица-столбец с N строками, а
Ваесть матрица-столбец с N строками, а 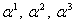 Ваи
Ваи 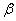 ВатАУ матрицы, имеющие по N строк и столбцов. Уравнение (1.5) и известно как уравнение Дирака.
ВатАУ матрицы, имеющие по N строк и столбцов. Уравнение (1.5) и известно как уравнение Дирака.
Теперь найдем выражения для плотности и тока, которые соответствуют уравнению (1.5). Так как мы хотим сохранить для 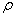 Вапривычное определение, то полагаем
Вапривычное определение, то полагаем
 Ва(1.6а)
Ва(1.6а)
или в матричной записи
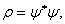 Ва(1.6б)
Ва(1.6б)
где 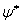 ВатАУ величина, эрмитово сопряженная
ВатАУ величина, эрмитово сопряженная 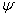 , а следовательно, являющаяся матрицей-строкой, содержащей одну строку и N столбцов. Выражения (1.6) для плотности явно положительны определены и, таким образом, отвечают основным требованиям Дирака. Далее потребуем, чтобы
, а следовательно, являющаяся матрицей-строкой, содержащей одну строку и N столбцов. Выражения (1.6) для плотности явно положительны определены и, таким образом, отвечают основным требованиям Дирака. Далее потребуем, чтобы 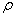 Ваудовлетворяла уравнению неразрывности
Ваудовлетворяла уравнению неразрывности
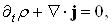 (1.7)
(1.7)
где ток j еще должен быть определен. Можно надеяться, что тогда будет применима обычная вероятностная интерпретация. Величина 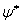 Ваудовлетворяет уравнению
Ваудовлетворяет уравнению
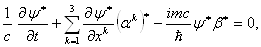 Ва(1.8)
Ва(1.8)
которое получается эрмитовым сопряжением уравнением (1.5). Как и выше, "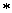 " является знаком эрмитова сопряжения, при котором матрицы
" является знаком эрмитова сопряжения, при котором матрицы 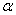 Ваи
Ваи 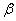 Ватранспонируются и комплексно сопрягаются, например
Ватранспонируются и комплексно сопрягаются, например
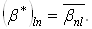 Ва(1.9)
Ва(1.9)
Перестановка 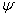 Вас
Вас 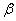 Вав (1.8) необходима потому, что
Вав (1.8) необходима потому, что 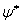 ВатАУ строка, и, следовательно,
ВатАУ строка, и, следовательно, 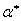 Ваи
Ваи 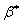 Вадолжны стоять после нее (а не перед ней).
Вадолжны стоять после нее (а не перед ней).
Уравнение неразрывности типа (1.7) можно теперь вывести из уравнений (1.5) и (1.8), если первое умножить на 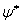 Васлева, а второе тАУ на
Васлева, а второе тАУ на 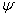 Васправа и сложить получившиеся результаты. Это приводит к уравнению
Васправа и сложить получившиеся результаты. Это приводит к уравнению
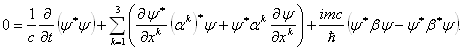 Ва(1.10)
Ва(1.10)
Последний член не содержит производных. Поэтому, если мы хотим отождествить уравнение (1.10) с уравнением (1.7), нужно добиться, чтобы этот член был равен нулю. Это можно достигнуть, если потребовать, чтобы
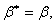 Ва(1.11)
Ва(1.11)
то есть чтобы матрица 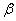 Вабыла эрмитовой. Для отождествления второй группы членов в уравнении (1.10) с дивергенцией мы потребуем далее, чтобы
Вабыла эрмитовой. Для отождествления второй группы членов в уравнении (1.10) с дивергенцией мы потребуем далее, чтобы
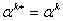 Ва(1.12)
Ва(1.12)
Другими словами, и 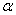 Ваи
Ваи 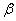 Вадолжны быть эрмитовыми матрицами. Другой путь, ведущий к тому же результату,тАФ переписать уравнение (1.5) в гамильтоновой форме:
Вадолжны быть эрмитовыми матрицами. Другой путь, ведущий к тому же результату,тАФ переписать уравнение (1.5) в гамильтоновой форме:
 (1.13)
(1.13)
Ясно, что для эрмитовости H матрицы 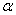 Ваи
Ваи 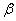 Вадолжны быть эрмитовыми. Сравнивая (1.7) с (1.10), заключаем
Вадолжны быть эрмитовыми. Сравнивая (1.7) с (1.10), заключаем
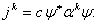 Ва(1.14)
Ва(1.14)
Для вывода дальнейших свойств матриц 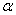 Ваи
Ваи 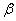 Ванужно исследовать условия, которое накладывает требование, чтобы функция
Ванужно исследовать условия, которое накладывает требование, чтобы функция 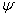 Ваудовлетворяла уравнению
Ваудовлетворяла уравнению
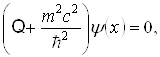 Ва(1.3)
Ва(1.3)
Где
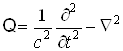
С этой целью умножим уравнение (1.5) на оператор
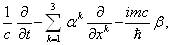
Который приведет к появлению вторых производных. Члены с 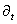 Ваи со смешанными пространственно-временными производными сокращаются, и мы получаем
Ваи со смешанными пространственно-временными производными сокращаются, и мы получаем
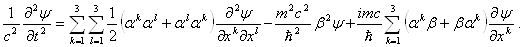 Ва(1.15)
Ва(1.15)
Мы симметризовали здесь член 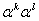 , что можно зделать вследствие коммутации
, что можно зделать вследствие коммутации  Ваи
Ваи 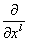 . Чтобы уравнение (1.15) согласовалось с уравнением Клейна-Гордона, необходимо его правую часть свести к
. Чтобы уравнение (1.15) согласовалось с уравнением Клейна-Гордона, необходимо его правую часть свести к
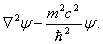
Это накладывает следующие условия:
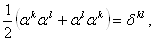 Ва(1.16)
Ва(1.16)
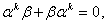 Ва(1.17)
Ва(1.17)
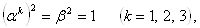 Ва(1.18)
Ва(1.18)
то есть матрицы 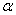 Вадолжны антикоммутировать между собой и с матрицей
Вадолжны антикоммутировать между собой и с матрицей 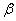 , а квадрат каждой из четырех матриц должен быть равен единице.
, а квадрат каждой из четырех матриц должен быть равен единице.
В уравнении (1.16) символ 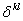 ВатАУ контравариантный символ Кронекера, значение которого совпадает с
ВатАУ контравариантный символ Кронекера, значение которого совпадает с 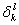 , где
, где 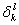 ВатАУ смешанный символ Кронекера, причем
ВатАУ смешанный символ Кронекера, причем
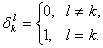
В практических приложениях нет необходимости использовать явное представление для 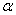 Ваи
Ваи 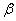 ; достаточно знать, что они эрмитовы и обладают свойствами (1.16) тАУ (1.18). Более того, при решении задач удобнее обходиться без явного вида матриц. Однако их явное представление легко можно получить. Прежде всего замечаем, что размерность N должна быть четной.
; достаточно знать, что они эрмитовы и обладают свойствами (1.16) тАУ (1.18). Более того, при решении задач удобнее обходиться без явного вида матриц. Однако их явное представление легко можно получить. Прежде всего замечаем, что размерность N должна быть четной.
На самом деле. Перепишем соотношение (1.17) в виде
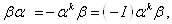 (1.19)
(1.19)
где I тАУ единичная матрица. Взяв детерминант от обеих частей равенства (1.19), получим
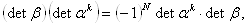 (1.20)
(1.20)
где учтено, что 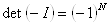 . Отсюда
. Отсюда 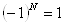 , и число N должно быть четным.
, и число N должно быть четным.
Придадим уравнению Дирака ковариантный вид. В записи
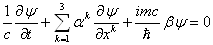 Ва(1.5)
Ва(1.5)
для уравнения Дирака пространственные производные умножены на матрицы, а временные нет. Чтобы устранить это неравноправие, умножим уравнение (1.5) слева на матрицу 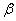 :
:
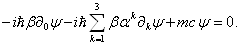 (1.21)
(1.21)
Уравнение примет более симметричный вид, если ввести матрицы
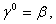 Ва(1.22)
Ва(1.22)
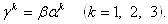 Ва(1.23)
Ва(1.23)
Отметим, что при таком определении матрица 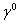 Ваэрмитова и
Ваэрмитова и 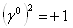 ,а матрицы
,а матрицы 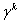 ВатАУ антиэрмитовы, то есть
ВатАУ антиэрмитовы, то есть 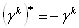 , и
, и 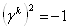 . Отсюда следует, что матрицы
. Отсюда следует, что матрицы 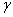 Ваудовлетворяют перестановочным соотношениям
Ваудовлетворяют перестановочным соотношениям
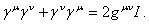 (1.24)
(1.24)
С помощью 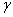 -матриц уравнение (1.21) записывается в виде
-матриц уравнение (1.21) записывается в виде
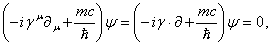 Ва(1.25)
Ва(1.25)
где снова использовано соглашение о суммировании. Уравнение (1.25) и является ковариантной формой уравнения Дирака, в которой пространственные и временные производные входят равноправно.
Для упрощения полученного уравнения введем обозначения. Обозначим при помощи 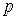 Вавеличину
Вавеличину
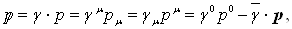 (1.26)
(1.26)
где матрицы 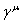 Ваопределяются согласно
Ваопределяются согласно
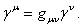 Ва(1.27)
Ва(1.27)
С помощью этого обозначения и в естественной системе единиц уравнение Дирака записывается в виде
 Ва(1.28)
Ва(1.28)
Где
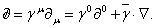 (1.29)
(1.29)
Ток и плотность можно записать с помощью матриц 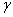 Васледующим образом. Умножая равенство (1.23) на матрицу
Васледующим образом. Умножая равенство (1.23) на матрицу 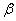 Васлева, находим
Васлева, находим 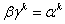 , а поэтому ток
, а поэтому ток
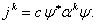 Ва(1.14)
Ва(1.14)
примет следующий вид
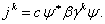 Ва(1.30)
Ва(1.30)
С помощью "сопряженной" волновой функции 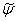 , определенно согласно
, определенно согласно
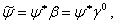 Ва(1.31)
Ва(1.31)
выражение для тока записывается в виде
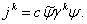 Ва(1.32)
Ва(1.32)
Аналогично через матрицы 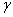 Вазаписывается и плотность
Вазаписывается и плотность
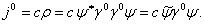 Ва(1.33)
Ва(1.33)
Уравнение для сопряженной функции 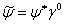 Ваполучают из уравнения (1.8), вставляя в каждом члене справа от
Ваполучают из уравнения (1.8), вставляя в каждом члене справа от 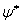 Вамножитель
Вамножитель 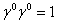 Ваи используя затем соотношения (1.11), (1.12) и (1.23). В естественной системе единиц это уравнение запишется так:
Ваи используя затем соотношения (1.11), (1.12) и (1.23). В естественной системе единиц это уравнение запишется так:
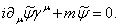 Ва(1.34)
Ва(1.34)
2. Матрица Дирака. Свойства матриц Дирака
Матрицы 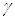 Ваобразуют совокупность гиперкомплексных чисел, удовлетворяющих перестановочным соотношениям
Ваобразуют совокупность гиперкомплексных чисел, удовлетворяющих перестановочным соотношениям 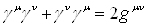 .
.
Рассмотрим 16 элементов:
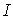
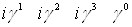
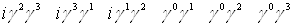
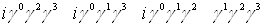
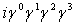
Все другие произведения матриц 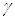 Вас помощью перестановочных соотношений могут быть сведены к одной из шестнадцати. Множитель i вставлен для того, чтобы квадрат каждого элемента был равен +1. Обозначим элементы в выписанном порядке при помощи
Вас помощью перестановочных соотношений могут быть сведены к одной из шестнадцати. Множитель i вставлен для того, чтобы квадрат каждого элемента был равен +1. Обозначим элементы в выписанном порядке при помощи 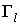 Ва(l=1, 2, тАж,16). Замечаем, что с точностью до множителей
Ва(l=1, 2, тАж,16). Замечаем, что с точностью до множителей 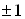 Ваили
Ваили 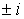 Вапроизведение любых двух элементов всегда равно третьему. Для каждого элемента
Вапроизведение любых двух элементов всегда равно третьему. Для каждого элемента 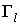 , за исключением
, за исключением 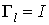 , всегда можно найти такой элемент
, всегда можно найти такой элемент  , что
, что 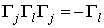 . Это утверждение мы докажем, но для этого укажем элемент
. Это утверждение мы докажем, но для этого укажем элемент  Вадля каждого
Вадля каждого 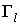 . Так, для l=2, тАж,5, т.е. для элементов второй строки списка,
. Так, для l=2, тАж,5, т.е. для элементов второй строки списка, 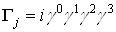 ; в случае третьей строки, например, элементу
; в случае третьей строки, например, элементу 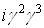 Васоответствует
Васоответствует  , так как
, так как 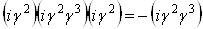 ; для всей четвертой строки
; для всей четвертой строки 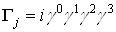 , а для пятой в качестве
, а для пятой в качестве  Ваможно выбрать, например,
Ваможно выбрать, например, 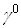 . Отсюда следует, что след любой матрицы
. Отсюда следует, что след любой матрицы 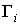 Вас
Вас 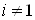 Варавен нулю, так как
Варавен нулю, так как

Шестнадцать элементов 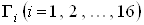 линейно независимы, другими словами, равенство
линейно независимы, другими словами, равенство 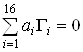 Васправедливо только тогда, когда все
Васправедливо только тогда, когда все 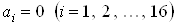 .
.
Докажем. Вычисляя след от 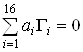 , получим
, получим 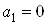 . Аналогично, последовательно умножая уравнение на каждую из
. Аналогично, последовательно умножая уравнение на каждую из 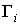 Ваи вычисляя след, получаем, что
Ваи вычисляя след, получаем, что 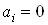 , что и требовалось доказать. Отсюда следует, что гиперкомплексные числа нельзя представить матрицами размерности, меньшей
, что и требовалось доказать. Отсюда следует, что гиперкомплексные числа нельзя представить матрицами размерности, меньшей 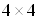 , так как при меньшей размерности не существует 16 линейно независимых матриц. Обратно,
, так как при меньшей размерности не существует 16 линейно независимых матриц. Обратно, 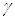 Ваможно представить матрицами, размерностью
Ваможно представить матрицами, размерностью 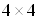 , потому что среди этих матриц имеется ровно 16 линейно независимых (так как число элементов
, потому что среди этих матриц имеется ровно 16 линейно независимых (так как число элементов 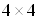 Ваматрицы равно 16). Это представление (как и все ему эквивалентные) оказывается неприводимым. Любое другое представление может быть приведено к виду
Ваматрицы равно 16). Это представление (как и все ему эквивалентные) оказывается неприводимым. Любое другое представление может быть приведено к виду

где 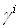 ВатАУ матрицы размерности
ВатАУ матрицы размерности 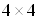 .
.
Из линейной независимости 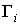 Васледует, что всякая
Васледует, что всякая 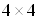 Ваматрица X может быть записана в виде
Ваматрица X может быть записана в виде
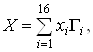 Ва(2.1)
Ва(2.1)
Где
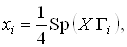 Ва(2.2)
Ва(2.2)
Так как 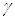 -матрицы неприводимы, то по лемме Шура следует, что любая
-матрицы неприводимы, то по лемме Шура следует, что любая 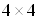 Ваматрица, коммутирующая со всеми матрицами
Ваматрица, коммутирующая со всеми матрицами 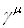 , кратна единичной матрице.
, кратна единичной матрице.
На самом деле. Пусть X будет матрицей, коммутирующей со всеми матрицами 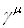 , а следовательно, и со всеми
, а следовательно, и со всеми 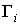 . Представим X в виде
. Представим X в виде
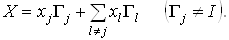 (2.3)
(2.3)
Пусть 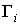 Ватакая матрица, что
Ватакая матрица, что 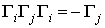 . По предположению,
. По предположению,  , а потом, умножая (2.3) слева и справа на
, а потом, умножая (2.3) слева и справа на 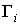 , получаем
, получаем
 Ва(2.4)
Ва(2.4)
где множители 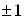 Вавозникают в зависимости от того, коммутируют или антикоммутируют
Вавозникают в зависимости от того, коммутируют или антикоммутируют 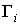 Ваи
Ваи 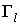 Вадруг с другом. Умножая (2.3) и (2.4) на
Вадруг с другом. Умножая (2.3) и (2.4) на 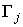 Ваи вычисляя след, получаем, что
Ваи вычисляя след, получаем, что 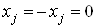 . Так как в качестве
. Так как в качестве 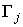 Вабралась любая из матриц Г, за исключением единичной, то единственный отличный от нуля коэффициент разложения (2.3) есть
Вабралась любая из матриц Г, за исключением единичной, то единственный отличный от нуля коэффициент разложения (2.3) есть 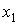 , что и требовалось доказать.
, что и требовалось доказать.
Основная теорема о матрицах 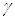 Вагласит: если даны две системы
Вагласит: если даны две системы 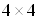 Ваматриц
Ваматриц 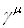 Ваи
Ваи 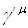 , удовлетворяющих перестановочным соотношениям
, удовлетворяющих перестановочным соотношениям
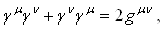 (2.5а)
(2.5а)
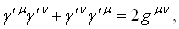 (2.5б)
(2.5б)
то существует такая несобственная матрица S, что
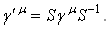 Ва(2.6)
Ва(2.6)
Явный вид S дается выражением
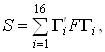 Ва(2.7)
Ва(2.7)
где F тАУ произвольная 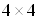 Ваматрица, которая может быть выбрана таким образом, чтобы матрица S была несобственной. Совокупность 16 линейно независимых
Ваматрица, которая может быть выбрана таким образом, чтобы матрица S была несобственной. Совокупность 16 линейно независимых 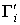 Вапостроена из матриц
Вапостроена из матриц 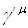 Ваточно так же, как были построены
Ваточно так же, как были построены 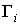 Ваиз
Ваиз 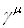 . Для доказательства теоремы заметим, что если
. Для доказательства теоремы заметим, что если 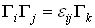 , где
, где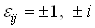 , то тогда
, то тогда 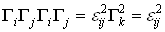 , так что
, так что  . Отметим, что в штрихованной системе число
. Отметим, что в штрихованной системе число 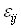 Вабудет тем же самым, т.е
Вабудет тем же самым, т.е 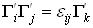 , так как его значение определяется только перестановочными соотношениями, а они одинаковы для обеих совокупностей матриц. Так как
, так как его значение определяется только перестановочными соотношениями, а они одинаковы для обеих совокупностей матриц. Так как 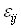 Варавно либо
Варавно либо 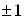 , либо
, либо 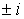 , то
, то 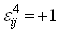 . Воспользовавшись для S представлением (2.7), получаем
. Воспользовавшись для S представлением (2.7), получаем
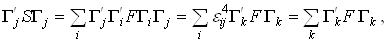 (2.8)
(2.8)
с учетом того, что при фиксированном 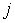 Ваматрица
Ваматрица  , находящаяся под знаком суммы по
, находящаяся под знаком суммы по 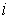 , пробегает все значения 16 элементов алгебры. Это позволило заменить сумму по
, пробегает все значения 16 элементов алгебры. Это позволило заменить сумму по 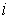 Васуммой по
Васуммой по 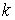 . Таким образом, получаем
. Таким образом, получаем
 Ва(2.9)
Ва(2.9)
Так как матрицы 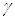 Ванеприводимы, то по лемме Шура матрица S является несобственной. Кроме того, с точностью до множителя матрица S определяется однозначно. В самом деле, предположим, что таких матриц S имеется две, скажем
Ванеприводимы, то по лемме Шура матрица S является несобственной. Кроме того, с точностью до множителя матрица S определяется однозначно. В самом деле, предположим, что таких матриц S имеется две, скажем 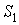 Ваи
Ваи 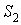 , так что
, так что 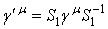 Ваи
Ваи 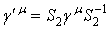 . Тогда исключая
. Тогда исключая 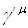 , получаем
, получаем 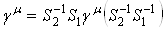 , т.е. что матрица
, т.е. что матрица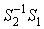 Вакоммутирует со всеми матрицами
Вакоммутирует со всеми матрицами 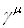 Ваи, следовательно, кратен единичной матрице. Отсюда
Ваи, следовательно, кратен единичной матрице. Отсюда 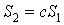 . Часто бывает удобным наложить условие нормировки
. Часто бывает удобным наложить условие нормировки 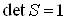 , которая определяет матрицу S уже с точностью до множителя
, которая определяет матрицу S уже с точностью до множителя  , равного
, равного 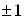 , или
, или 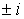 .
.
Интересен частный случай соотношения (2.7), когда 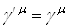 . В этом случае
. В этом случае 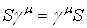 , и S есть матрица, кратная единичной:
, и S есть матрица, кратная единичной: 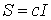 . Тогда матричный элемент соотношения (2.7) с индексами
. Тогда матричный элемент соотношения (2.7) с индексами 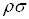 Варавен
Варавен
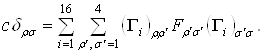 Ва(2.10)
Ва(2.10)
Так как это тождество верно при любом выборе матрицы F, то из него следует
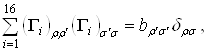 Ва(2.11)
Ва(2.11)
где 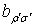 ВатАУ некоторая постоянная. Для определения этой постоянной свернем индексы
ВатАУ некоторая постоянная. Для определения этой постоянной свернем индексы 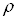 Ваи
Ваи 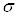 :
:
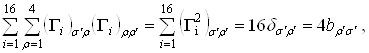 Ва(2.12)
Ва(2.12)
откуда 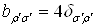 , и, таким образом, приходим к тождеству
, и, таким образом, приходим к тождеству
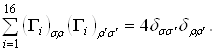 (2.13)
(2.13)
3. Спиноры
Связь между координатами точек трехмерного пространства для двух наблюдателей, системы координат которых повернуты друг относительно друга вокруг общего начала, имеет вид
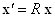 Ва(3.1а)
Ва(3.1а)
или
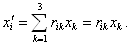 Ва(3.1б)
Ва(3.1б)
Длина вектора и угол между векторами остаются неизменными при вращениях, т.е.
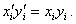 (3.2)
(3.2)
Следовательно,
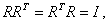 (3.3)
(3.3)
т. е. вращения представляются ортогональными матрицами. Из (3.3) следует
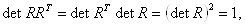
так что для матриц, удовлетворяющих (3.3), 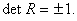 ВаПреобразования, для которых
ВаПреобразования, для которых 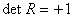 , называют собственными преобразованиями или вращениями, а те, для которых
, называют собственными преобразованиями или вращениями, а те, для которых 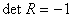 , несобственными ортогональными преобразованиями. Примером несобственного преобразования является отражение в начале координат, которое представляется матрицей
, несобственными ортогональными преобразованиями. Примером несобственного преобразования является отражение в начале координат, которое представляется матрицей
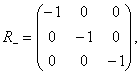 Ва(3.4)
Ва(3.4)
причем 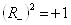 . Преобразование
. Преобразование 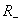 Васоответствует переходу от правой системы координат к левой. Каждое несобственное преобразование
Васоответствует переходу от правой системы координат к левой. Каждое несобственное преобразование 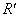 Вас
Вас 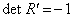 Ваможет быть записано в виде
Ваможет быть записано в виде 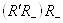 , т. е. как отражение
, т. е. как отражение 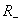 , вслед за которым уже выполняется вращение; в самом деле,
, вслед за которым уже выполняется вращение; в самом деле,
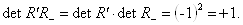
Совокупность всех вращений в евклидовом трехмерном пространстве образует группу тАУ группу вращений. Группа всех вращений вместе с отражениями называется ортогональной группой. Так как каждый элемент группы может быть охарактеризован заданием трех непрерывно изменяющихся параметров (например, направляющих косинусов оси, вокруг которых совершается вращение, и угла поворота), то группа вращений является непрерывной трехпараметрической группой. Число параметров группы называется размерностью группы.
Вообще представление какой-либо группы G есть отображение (соответствие), сопоставляющее каждому элементу g из G линейный оператор Tg, действующий в некотором векторном пространстве V, и притом такое, что сохраняется таблица умножения для группы, а единица e группы G отображается тождественным преобразованием I в V.
Подпространство V1 пространства V называют инвариантным подпространством относительно представления Tg, если все векторы 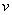 Вав V1 преобразуются по Tg в векторы
Вав V1 преобразуются по Tg в векторы 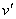 , снова принадлежащие V1, и это справедливо при всех преобразованиях Tg.
, снова принадлежащие V1, и это справедливо при всех преобразованиях Tg.
Каждое вращение является вращением вокруг некоторой оси, так что она может быть характеризовано заданием оси вращения, т.е. оси, вокруг которой осуществляется поворот и величины угла поворота. Таким образом, вращение может быть задано вектором 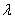 , направленным вдоль оси вращения и равным по величине углу поворота. Так, вращение вокруг оси 1 задается вектором
, направленным вдоль оси вращения и равным по величине углу поворота. Так, вращение вокруг оси 1 задается вектором 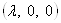 , вокруг оси 2 тАУ вектором
, вокруг оси 2 тАУ вектором 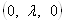 Ваи т.д. Элемент группы может рассматриваться как функция
Ваи т.д. Элемент группы может рассматриваться как функция 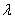 , т.е.
, т.е. 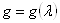 , и тоже относится к представлению:
, и тоже относится к представлению: 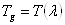 . Вектор
. Вектор 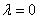 Васоответствует тождественному преобразованию
Васоответствует тождественному преобразованию
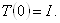 Ва(3.5)
Ва(3.5)
Рассмотрим бесконечно малые вращения вокруг той или иной оси. Их важность связана с тем, что они порождают однопараметрические подгруппы и что любое конечное вращение может быть построено как последовательность бесконечно малых. Бесконечно малые вращения коммутируют друг с другом, тогда как конечные вращения в общем случае не коммутируют.
Пусть 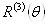 Вабудет матрицей поворота на угол
Вабудет матрицей поворота на угол 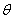 Вавокруг оси 3, и пусть определена матрица
Вавокруг оси 3, и пусть определена матрица
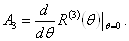 Ва(3.6)
Ва(3.6)
Оператор 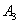 Ваназывают генератором вращения вокруг оси 3. При бесконечно малом
Ваназывают генератором вращения вокруг оси 3. При бесконечно малом 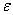 Ваможно записать
Ваможно записать
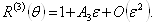 Ва(3.7)
Ва(3.7)
Теперь вращения 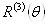 Вана угол
Вана угол 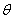 Вавокруг оси 3 может рассматриваться как результат n поворотов на угол
Вавокруг оси 3 может рассматриваться как результат n поворотов на угол 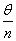 . Поэтому мы можем записать
. Поэтому мы можем записать
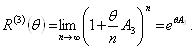 Ва(3.8)
Ва(3.8)
Аналогичным образом можно определить генераторы вращений вокруг осей 1 и 2. Так как
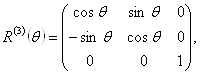 Ва(3.9)
Ва(3.9)
то явным видом для 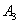 Вабудет
Вабудет
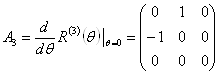 Ва(3.10а)
Ва(3.10а)
и аналогично
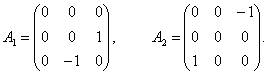 Ва(3.10б)
Ва(3.10б)
Можно проверить, что генераторы 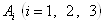 Ваудовлетворяют следующим перестановочным соотношениям:
Ваудовлетворяют следующим перестановочным соотношениям:
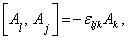 (3.11)
(3.11)
где 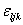 ВатАУ полностью антисимметричный тензор 3-го ранга с компонентами, равными +1, если ljk есть четная перестановка 1 2 3, равными тАУ1, если перестановка нечетная, и равными нулю в остальных случаях. Отметим, что оператор отражения
ВатАУ полностью антисимметричный тензор 3-го ранга с компонентами, равными +1, если ljk есть четная перестановка 1 2 3, равными тАУ1, если перестановка нечетная, и равными нулю в остальных случаях. Отметим, что оператор отражения 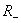 Вакоммутирует со всеми вращениями
Вакоммутирует со всеми вращениями
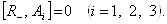 Ва(3.12)
Ва(3.12)
Бесконечно малый поворот вокруг 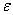 Вана угол
Вана угол  Ваможет быть записан в виде
Ваможет быть записан в виде
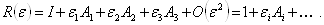 Ва(3.13)
Ва(3.13)
Соответствующий оператор представления запишем
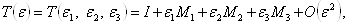 Ва(3.14)
Ва(3.14)
где 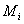 Ваобразуют представление генераторов и удовлетворяют перестановочным соотношениям
Ваобразуют представление генераторов и удовлетворяют перестановочным соотношениям
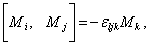 Ва(3.15)
Ва(3.15)
Пусть операторы 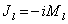 . Эти операторы будут эрмитовыми и удовлетворяют перестановочным соотношениям для операторов момента количества движения
. Эти операторы будут эрмитовыми и удовлетворяют перестановочным соотношениям для операторов момента количества движения
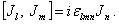 (3.16)
(3.16)
В случае группы вращений со всеми генераторами коммутирует оператор 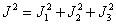 , и поэтому он является инвариантом группы. Его собственные значения, как известно из теории оператора момента количества движения, равны
, и поэтому он является инвариантом группы. Его собственные значения, как известно из теории оператора момента количества движения, равны 
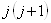 , где
, где 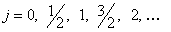 .Таким образом, каждое неприводимое представление характеризуется положительным целым или полуцелым j, включая 0. Размерность неприводимого представления равна
.Таким образом, каждое неприводимое представление характеризуется положительным целым или полуцелым j, включая 0. Размерность неприводимого представления равна 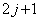 Вапри любом весе j, целым или полуцелым. Переходя к классификации неприводимых представлений ортогональной группы, заметим, что линейный оператор
Вапри любом весе j, целым или полуцелым. Переходя к классификации неприводимых представлений ортогональной группы, заметим, что линейный оператор 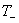 , соответствующий операции отражения
, соответствующий операции отражения 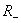 , коммутирует со всеми вращениями.
, коммутирует со всеми вращениями.
В теории представления групп, осуществляемых комплексными матрицами, фундаментальное значение имеет лемма Шура, в которой доказывается, что необходимое и достаточное условие для неприводимости представления состоит в том, чтобы единственными матрицами, коммутирующими со всеми матрицами представления, были матрицы, кратные единичной.
По лемме Шура в каждом неприводимом представлении он должен быть кратен единичному оператору. Таким образом, неприводимые представления ортогональной группы классифицируются парой индексов 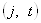 , где второй индекс является собственным значением
, где второй индекс является собственным значением 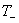 , соответствующий данному представлению. При целых j имеем
, соответствующий данному представлению. При целых j имеем 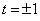 Ва(ибо
Ва(ибо 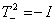 ), так что существуют два различных неприводимых представления ортогональной группы. В одном из них
), так что существуют два различных неприводимых представления ортогональной группы. В одном из них 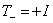 , в другом
, в другом 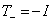 .
.
При 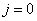 Вапредставление одномерно, каждый элемент группы отображается единичным элементом, а генераторы тождественно равны нулю. Представление, в котором
Вапредставление одномерно, каждый элемент группы отображается единичным элементом, а генераторы тождественно равны нулю. Представление, в котором 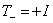 , назовем скалярным, а то, в котором
, назовем скалярным, а то, в котором 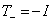 , тАУ псевдоскалярным.
, тАУ псевдоскалярным.
При 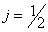 Вапредставление группы вращений двумерно, и генераторы
Вапредставление группы вращений двумерно, и генераторы 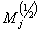 Вамогут быть реализованы эрмитовыми матрицами Паули
Вамогут быть реализованы эрмитовыми матрицами Паули 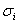 , умноженными на
, умноженными на 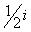 :
:
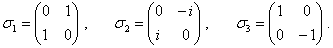 (3.17)
(3.17)
Они удовлетворяют соотношению
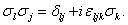 (3.18)
(3.18)
Таким образом, в представлении веса 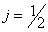 Ваоператор поворота на угол
Ваоператор поворота на угол 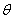 Вавокруг оси 3 записывается в виде
Вавокруг оси 3 записывается в виде
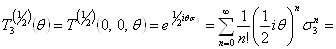
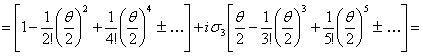
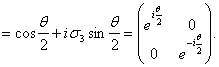 (3.19а)
(3.19а)
Аналогично, в представлении 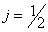 Вазаписываются и операторы поворота на угол
Вазаписываются и операторы поворота на угол 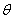 Вавокруг осей 1 и 2:
Вавокруг осей 1 и 2:
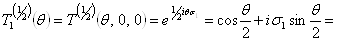
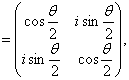 (3.19б)
(3.19б)
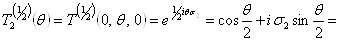
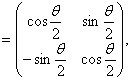 (3.19в)
(3.19в)
Отметим, что матрицы 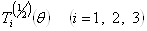 Ваунитарны и имеют детерминант, равный единице. Отметим также, что поворот на угол
Ваунитарны и имеют детерминант, равный единице. Отметим также, что поворот на угол 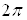 Вавокруг любой оси дает
Вавокруг любой оси дает
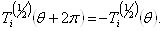 (3.20)
(3.20)
Таким образом, представление двузначно, и соответствие между элементами группы и операторами можно выразить 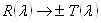 .
.
При 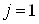 Вапредставление трехмерно, и в качестве матричного представления генераторов
Вапредставление трехмерно, и в качестве матричного представления генераторов 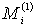 Ваможно взять матрицы
Ваможно взять матрицы 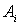 , определенные выше в виде (3.10а) и (3.10б). Обычное же квантово-механическое представление для
, определенные выше в виде (3.10а) и (3.10б). Обычное же квантово-механическое представление для 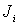 Вапри
Вапри 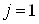 Ваимеет вид
Ваимеет вид
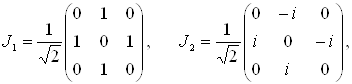
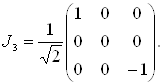 Ва(3.21)
Ва(3.21)
Оно унитарно эквивалентно представлению, полученному для 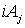 :
: 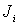 Васоответствует базису
Васоответствует базису 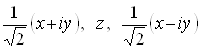 , вместо обычного декартова базиса
, вместо обычного декартова базиса 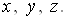
Величины 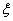 , которые при вращении системы координат
, которые при вращении системы координат
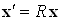 Ва(3.22)
Ва(3.22)
преобразуются по закону
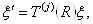 Ва(3.23)
Ва(3.23)
называют скалярами при 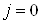 , спинорами 1-го ранга при
, спинорами 1-го ранга при 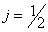 , векторами при
, векторами при 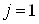 Ваи т.д. При бесконечно малых поворотах на угол
Ваи т.д. При бесконечно малых поворотах на угол 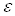 Вавокруг l-ой оси закон преобразования (3.23) принимает вид
Вавокруг l-ой оси закон преобразования (3.23) принимает вид
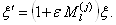 Ва(3.24)
Ва(3.24)
Таким образом, скаляр есть однокомпонентная величина, которая при вращениях  Вапреобразуется по закону
Вапреобразуется по закону  . Спинор 1-го ранга является двухкомпонентной величиной
. Спинор 1-го ранга является двухкомпонентной величиной
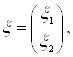 Ва(3.25)
Ва(3.25)
которая при бесконечно малых поворотах на угол 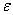 Вавокруг l-ой оси
Вавокруг l-ой оси
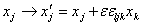 Ва(3.26)
Ва(3.26)
преобразуется по закону
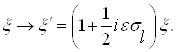 Ва(3.27)
Ва(3.27)
Как было отмечено выше, при вращениях на любой конечный угол спинор 1-го ранга преобразуется при помощи унитарной матрицы размерностью 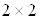 Ваи с детерминантом, равным единице. Наконец, вектор является трехкомпонентной величиной
Ваи с детерминантом, равным единице. Наконец, вектор является трехкомпонентной величиной
 Ва(3.28)
Ва(3.28)
компоненты которой 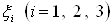 Вапри вращении (3.22) преобразуются так же, как сами координаты.
Вапри вращении (3.22) преобразуются так же, как сами координаты.
Сопряжение спинора 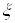 Вавыполняется обычным образом путем транспонирования и комплексного сопряжения. Таким образом, при
Вавыполняется обычным образом путем транспонирования и комплексного сопряжения. Таким образом, при 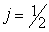 Васпинор
Васпинор 
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Волоконно-оптические датчики температуры на основе решеток показателя преломления
Время и пространство - идеалистические понятия