Кинематический и силовой расчёт механизма. Определение осевого момента инерции маховика. Проектирование профиля кулачкового механизма. Проектирование зубчатого зацепления. Проектирование планетарного механизма
Змiст
Вступ 3
1.дКiнематичне i силове дослiдження механiзму 4
1.1 Вихiднi данн 4
1.2 Структурний аналiз механiзму 5
1.3 Побудова положень механiзму 6
1.4 Визначаiмо швидкiсть точок i кутову швидкiсть ланок 6
1.5 Визначення прискорення точок та кутове прискорення ланок 8
1.6 Силовий розрахунок 11
2.дВизначення осьового моменту iнерцii маховика 18
2.1 Вихiднi даннi 18
2.2 Визначення сили Q 18
2.3 Визначення привiдного моменту 19
2.4 Побудова графiкiв Мпр=ƒ(φ), AQ= ƒ(φ), Ap= ƒ(φ), ΔE= ƒ(φ) 19
2.5 Побудова графiка Jпр=ƒ(φ) 20
2.6 Побудова дiаграми енергомас 22
3. Проектування профiлю кулачкового механiзму 23
3.1 Вихiднi даннi 23
3.2 Визначення закону руху штовхача 23
3.3 Знаходження мiнiмального радiуса кулачка 25
3.4 Проектування профiлю кулачка 27
4. Проектування зубчатого зачеплення 29
4.1 Вихiднiданнi 29
4.3 Проектування зачеплення 31
4.4 Визначаiмо величини параметрiв якостi 33
4.5 Проектування планетарноi передачi 33
4.5.1 Вихiднi даннi 33
4.5.2 Розрахунок параметрiв планетарноi передачi 34
4.5.3 Побудова планiв лiнiйних i кутових швидкостей 35
5. Використана лiтература 37
Вступ
Розвиток сучасноi науки та технiки нерозривно звтАЩязан з бiдуванням нових машин, пiдвищуванням продуктивностi та полегшуванням працi людей, а також забезпечують засоби дослiдження законiв природи та життя людини.
З розвитком сучасноi науки та технiки все ширше використовуються системи машин автоматичноi дii. Сукупнiсть машин-автоматiв, зтАЩiднаних мiж собою та призначених для здiйснення певного технологiчного процесу називаiться автоматичною лiнiiю.
В теорii механiзмiв вивчаються загальнi методи дослiдження властивостей механiзмiв та проектування iх схеми незалежно вiд конкретного призначення машини, приладу та апарата.
В теорii машин розглядаються загальнi методи проектування машин. Обидвi частини теорii механiзмiв i машин невiдтАЩiмно звтАЩязанi мiж собою, так як механiзми складають основу майже кожноi машини.
При вивченнi загальних властивостей механiзмiв необхiдно видiлити найбiльш суттiвi загальнi ознаки механiзмiв, вiдвертаючись вiд приватних ознак, належних конкретному механiзму. Наприклад, при вивченнi кiнематичних властивостей механiзмiв достатнього мати його схему, складаючу вiдомостi, необхiднi для визначення кiнематичних характеристик : перемiщення, швидкостi, прискорення.
Задачi теорii машин та механiзмiв дуже рiзноманiтнi, але важливостi з них можна розподiлити по трьом роздiлам:
- аналiз механiзмiв;
- синтез механiзмiв;
- теорiя машин-автоматiв.
Аналiз механiзмiв становить дослiдження кiнематичних i динамiчних властивостей механiзму по заданiй схемi, а синтез механiзму в проектуваннi схеми механiзму по заданим його властивостям
1.дКiнематичне i силове дослiдження механiзму.
1.1 Вихiднi даннi.
Транспортер (мал. 1)
Таблиця №1
Довжина ланок | ω1 | Маса ланок | ||||||
О1А | О2В | ВС | О1А | пол.А | ВА | ВС | пол.С | |
мм | мм | мм | 1/с | кг | кг | кг | кг | кг |
| 45 | 50 | 160 | 80 | 0,22 | 0,21 | 0,42 | 0,85 | 1,3 |
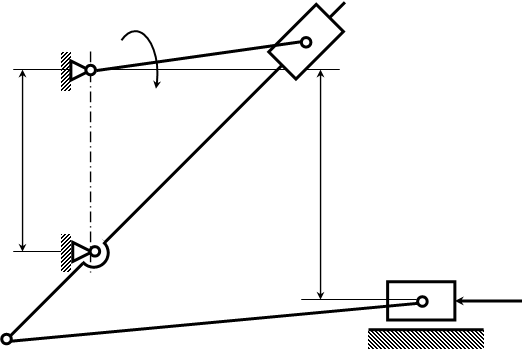
ω1
А
О1
Y1
Y2
О2
Q5
C
В
мал. 1).

1 2
3
6
5
5 6
4
мал. 2).
1.2 Структурний аналiз механiзму.
Виконуiмо аналiз кiнематичного ланцюгу (мал. 2):
1-6 тАУ обертальна кiнематична пара 5-го класу;
1-2 - обертальна кiнематична пара 5-го класу;
3-6 - обертальна кiнематична пара 5-го класу;
3-4 - обертальна кiнематична пара 5-го класу;
4-5 - обертальна кiнематична пара 5-го класу;
2-3 - поступальна кiнематична пара 5-го класу;
5-4 - поступальна кiнематична пара 5-го клас.
Проаналiзуiмо кiнематичнi ланки (мал. 2):
1 тАУ кривошип;
2 тАУ кулiса;
3 тАУ коромисло;
4 тАУ шатун;
5 тАУ повзун;
6 тАУ стояк.
Визначаiмо рухомiсть механiзму (мал.1) за формулою Чебишева:
![]()
де: n - кiлькiсть ланок;
Р5 тАУ кiлькiсть кiнематичних пар 5-го класу;
Р4 тАУ кiлькiсть кiнематичних пар 4-го класу.
Визначаiмо клас механiзму, який дорiвнюi найвищому класу групи Ассура входячоi до складу механiзму.
 5
5
4 дiада 2-го класу
 2-го виду
2-го виду
2
дiада 2-го класу
2-го виду
3
 1 механiзм 1-го класу
1 механiзм 1-го класу
(мал. 3)
Висновок: даний механiзм згiдно проведеного аналiзу вiдноситься до механiзму 2-го класу з рухомiстю рiвнiй одиницi. Це означаi те, що нам достатньо виконати ведучою лише одну ланку.
1.3 Побудова положень механiзму.
На кресленнi № 1 довiльно вибираiмо точку О1 . За розмiрами вiдкладаiмо точку О2 . Навколо точки О1 проводимо коло радiусом О1А. З точки О2 проводимо дугу радiуса О2В. До кола О1А з дуги, через точку О2 проведемо дотичнi, i добудуiмо iншi точки i ланки методом насiчок. Цi положення i i крайнiми положеннями механiзму. Кожен iз отриманих двох кутiв подiлимо на чотири рiвнi кути. РЖ добудуiмо iншi положення механiзму методом насiчок. Ми отримаiмо вiсiм положень механiзму.
1.4 Визначаiмо швидкiсть точок i кутову швидкiсть ланок.
Знайдемо швидкiсть точок i швидкiсть ланок для першого положення механiзму.
Визначаiмо швидкiсть точки А
![]()
На кресленнi № 1 довiльно вибираiмо полюс P i перпендикулярно ланцi О1А1 довжиною 50 мм провидимо вiдрiзок, який i i графiчним аналогом швидкостi.
Визначаiмо масштабний коефiцiiнт:
![]()
Швидкiсть точки А2 дорiвнюi швидкостi точки А1 , так як кулiса 2 i ланка 1 рухаiться разом.
Визначаiмо швидкiсть точки А3 графiчно, враховуючи систему:

де: VA2 ,VO2 тАУ переноснi швидкостi точки А3 ,
VA3A2 ,VA3O2 тАУ вiдноснi швидкостi точки А3 .
На планi з точки О2 проводимо паралельну до А3О2 , а з полюса P проводимо перпендикулярну до А3О2 . Точка iх перетину i буде точкою О3 . зтАЩiднуiмо ii з полюсом i отримуiмо швидкiсть точки А3 .
Знаходимо дiйсну швидкiсть точки А3:
![]()
Визначаiмо швидкiсть точки В за теоремою подiбностi (чергування букв, як на механiзмовi так i на плановi повинно спiвпадати при одному i тому ж напрямку обходу):
![]()
Знаходимо дiйсну швидкiсть точки В:
![]()
Визначаiмо швидкiсть точки С, вирiшуючи графiчно:
![]()
де: VВ тАУ переноснi швидкостi точки С,
VСВ тАУ вiдноснi швидкостi точки С.
З точки b проводимо перпендикуляр до ланки ВС i на перетинi його з горизонталлю, ми отримуiмо точку С i зтАЩiднавши ii з полюсом ми отримуiмо графiчний аналог швидкостi точки С.
Знаходимо дiйсну швидкiсть точки С:
![]()
Кутову швидкiсть ланки 3 знаходимо, як вiдношення вiдповiдноi вiдносноi швидкостi до ii довжини:
![]()
Аналогiчно знаходимо кутову швидкiсть i для ланки 4:
![]()
Для iнших положень механiзму розрахунки ведемо аналогiчно, а результати заносимо в таблицю № 2.
Таблиця № 2
0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
VA1=VA2 | м\с | 3,6 | 3,6 | 3,6 | 3,6 | 3,6 | 3,6 | 3,6 | 3,6 |
VA3=VA3O2 | м\с | 0 | 2,88 | 2,988 | 0 | 2,304 | 3,528 | 3,456 | 2,232 |
VB | м\с | 0 | 1,44 | 1,584 | 0 | 0,72 | 1,008 | 1,008 | 0,792 |
VC | м\с | 0 | 1,368 | 1,584 | 0 | 0,72 | 1,008 | 0,936 | 0,72 |
VA3A2 | м\с | 3,6 | 2,124 | 2,016 | 3,6 | 2,738 | 1,008 | 1,08 | 2,808 |
VCB | м\с | 0 | 0,3168 | 0,288 | 0 | 0,218 | 0,108 | 0,144 | 0,252 |
ω3 | 1\с | 0 | 28,8 | 31,68 | 0 | 14,4 | 20,16 | 20,16 | 15,84 |
ω4 | 1\с | 0 | 1,98 | 1,8 | 0 | 1,35 | 0,675 | 0,9 | 1,575 |
Так як кулiса рухаiться поступально, то ω2 не буде.
1.5 Визначення прискорення точок та кутове прискорення ланок.
Розглянемо прискорення точок та кутове прискорення ланок на прикладi першого положення.
Визначаiмо прискорення точки А:
![]()
На кресленнi № 1 довiльно вибираiмо полюс точку π i проводимо вiдрiзок πα , довжиною 100 мм i паралельно О1А, це i i графiчний аналог прискорення точки А.
Визначаiмо масштабний коефiцiiнт:
![]()
Прискорення точки А2 дорiвнюi прискорення точки А1 , так як вони рухаються разом.
Визначаiмо прискорення точки А3 графiчно вирiшуючи систему:

де: αA3A2K тАУ вiдносне карiолiсове прискорення точки А3
αА3А2τ, αА3О2τ тАУ вiдносне тангенцiальне прискорення точки А3
![]()
Перераховуiмо в графiчний аналог:
![]()
Порахуiмо вiдносне нормальне прискорення точки А3:
![]()
Перераховуiмо в графiчний аналог:
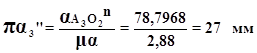
На планi (креслення №1) з точки α3 вiдкладаiмо перпендикулярно ланцi АО2 вiдрiзок α2α3тАЩ i з кiнця якого проводимо паралельно до АО2 промiнь. З полюса паралельно АО2 вiдкладаiмо вiдрiзок πα3тАЩтАЩ, з кiнця якого проводимо перпендикуляр до АО2 i на перетинi променя проведеного з точки α3тАЩ i з точки α3тАЩтАЩ ми отримуiмо точку α3 , зтАЩiднавши ii з полюсом ми отримаiмо графiчний аналог прискорення точки А3.
Знаходимо дiйсне прискорення точки А3:
![]()
Визначаiмо прискорення точки В за теоремою подiбностi:
![]()
Знаходимо дiйсне прискорення точки В:
![]()
Визначаiмо прискорення точки С вирiшуючи рiвняння графiчно:

де: αСВn тАУ вiдносне нормальне прискорення точки С
αСВτ тАУ вiдносне тангенцiальне прискорення точки С
Знайдемо вiдносне нормальне прискорення точки С:
![]()
Перерахуiмо в графiчний аналог:
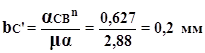
З точки В вiдкладаiмо вiдрiзок ВСтАЩ паралельно до ланки ВС. З кiнця якого проводимо перпендикуляр до перетину з горизонталлю. Точка iх перетину i буде точкою С, зтАЩiднавши ii з полюсом ми отримаiмо графiчний аналог прискорення точки С.
Знайдемо дiйсне прискорення точки С:
![]()
Кутове прискорення третьоi ланки знаходимо як вiдношення вiдповiдного вiдносного тангенцiального прискорення до його довжини:
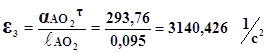
Аналогiчно розраховуiмо кутове прискорення для четвертоi ланки

Аналогiчно розраховуiмо все i для нульового положення механiзму.
1.6 Силовий розрахунок.
Силовий розрахунок розглянемо на прикладi першого положення механiзму.
Розрахуiмо моменти iнерцii:
![]()
![]()
де: JS3 , JS4 тАУ осьовий момент iнерцii.
Розраховуiмо сили iнерцii ланок i ваги:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Визначимо масштабний коефiцiiнт:
![]()
Перерахуiмо сили в графiчний аналог
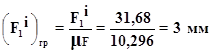
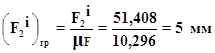
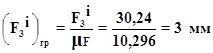
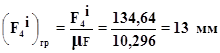
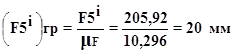
![]()
Перерахуiмо вагу в графiчний аналог:
![]()
![]()
![]()
![]()
![]()
Вилучаiмо з механiзму ланку 4-5. Складаiмо суму моментiв вiдносно точки В i знаходимо реакцiю R65.
![]()
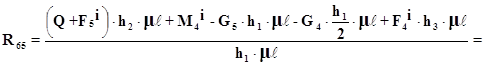

Перерахуiмо реакцiю R65 в графiчний аналог:
![]()
Складемо векторне рiвняння суми всiх сил дiючих на ланку 4-5:
![]()
Будуiмо силовий многокутник, з якого знаходимо реакцiю R34:
![]()
Знаходимо дiйсну реакцiю R34:
![]()
Вилучаiмо з механiзму ланку 3.
Складемо суму моментiв вiдносно точки О2 i знайдемо реакцiю R23:
![]()

Перерахуiмо реакцiю R23 в графiчний аналог:
![]()
Складемо векторну суму всiх сил дiючих на ланку:
![]()
Будуiмо силовий многокутник i знаходимо реакцiю R63:
![]()
Знайдемо дiйсне значення реакцii R63:
![]()
Вилучаiмо з механiзму ланку 2 i складаiмо векторне рiвняння:
![]()
Будуiмо силовий многокутник i знаходимо реакцiю R12:
![]()
Знайдемо дiйсне значення реакцii R12:
![]()
Вилучаiмо з механiзму ланку 1
Складаiмо суму моментiв вiдносно точки О, i знаходимо зрiвноважуючий момент:
![]()
![]()
Складемо векторне рiвняння усiх сил дiючих на ланку:
![]()
Будуiмо силовий многокутник i знаходимо реакцiю R61:
![]()
Знаходимо дiйсне значення реакцii R61:
![]()
1.7 Важiль Жуковського.
Вiзьмемо план швидкостi для першого положення i повернемо його на 90В°. Знесемо на нього усi зовнiшнi сили. Сума моментiв вiдносно полюса дасть нам зрiвноважуючий момент.
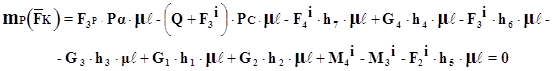

![]()
Розрахуiмо похибку мiж моментом отриманим з силового розрахунку i моментом отриманим з важеля
![]()
що задовольняi розрахункам.
1.8 Графiки.
На осi ординат вiдкладаiмо перемiщення повзуна, а на осi абсцис кут повороту кривошипу.
Визначимо масштабний коефiцiiнт
![]()
де: Х тАУ вiдрiзок на осi абсцис.
![]()
де: С0С3 тАУ вiдстань мiж мертвими положеннями;
Y3 - вiдстань на осi ординат на графiку, вiдповiдаючи вiдстанi мiж мертвими положеннями.
Кути повороту отриманi при побудовi положень механiзму, перераховуiмо за формулою у довжинi
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Перераховуiмо перемiщення повзуна:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На графiку на осi абсцис вiдкладаiмо довжини ℓi. З отриманих точок проводимо променi. На вiдповiдних променях вiдкладаiмо вiдповiднi довжини Si. ЗтАЩiднавши отриманi точки отримаiмо графiк перемiщень
![]()
Графiчно диференцiюючи цей графiк ми отримаiмо тАЬаналог швидкостейтАЭ в масштабi:
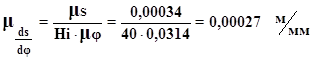
де: Нi тАУ вiдстань вiд осi ординат до полюса Р1.
Графiчно диференцiюючи графiк тАЬаналог швидкостейтАЭ, ми отримаiмо графiк тАЬаналог прискореннятАЭ в масштабi:
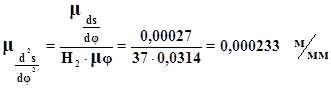
де: Н2 тАУ вiдстань вiд осi ординат до полюса Р2.
2.дВизначення осьового моменту iнерцii маховика.
2.1 Вихiднi даннi.
Вихiдними даними i даннi креслення № 1, крiм того додаiться закон змiни сили Q та коефiцiiнт нерiвномiрностi руху δ.
Qs

Sc (мал. 4)
Закон змiни сили Q
Коефiцiiнт нерiвномiрностi руху - ![]()
2.2 Визначення сили Q.
На кресленнi № 1, на вiсь перемiщення повзуна наносимо закон змiни сили Q i з точок робочого ходу проводимо вiдрiзки. Це i граничнi аналоги сил Q для положень робочого ходу, для холостого ходу сили Q приймаiмо рiвними нулю, так як закон змiни сили Q прямокутник.
Тому:
![]()
![]()
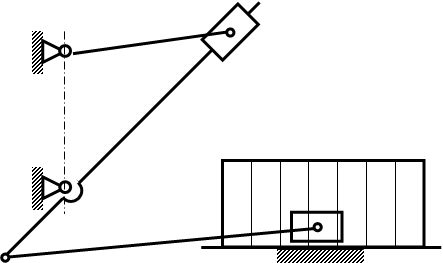
С1 С2 С3 С4 С5 С6 С7 С8
(мал. 5)
2.3 Визначення привiдного моменту.
Визначаiмо привiдний момент сили Q для кожного положення механiзму:
![]()
де : Vci тАУ швидкiсть повзуна в i-тому положеннi механiзму.
![]()
![]()
![]()
2.4 Побудова графiкiв Мпр=ƒ(φ), AQ= ƒ(φ), Ap= ƒ(φ), ΔE= ƒ(φ).
Визначаiмо масштабний коефiцiiнт

де : Y2 тАУ вiдстань на осi ординат, вiдповiдна даному приведеному моменту.
Будуiмо вiсь координат. По осi абсцис вiдкладаiмо кут повороту механiзму, та прораховуiмо аналогiчно як в пунктi 1.8. З отриманих точок проводимо променi, на яких вiдкладаiмо приведений момент перерахований в графiчний аналог:
![]()
![]()
ЗтАЩiднавши отриманi точки ми отримуiмо графiк приведеного моменту вiд сил Q, МQ= ƒ(φ).
Методом графiчного iнтегрування графiка приведеного моменту, отримуiмо графiк робiт сил Q, AQ= ƒ(φ). ЗтАЩiднавши початок i кiнець останнього, отримуiмо графiк робiт рушiйних сил Aр= ƒ(φ). Графiчно диференцiюючи графiк Aр= ƒ(φ), отримуiмо графiк моментiв рушiйних сил Мр= ƒ(φ).
Згiдно з формулою кiнетична енергiя дорiвнюi рiзницi робiт сил Q i рушiйних сил, тобто:
![]()
На графiку робiт замiряiмо рiзницю мiж графiками AQ= ƒ(φ) та Aр= ƒ(φ). Цю рiзницю наносимо на вiдповiднi променi системи координат. ЗтАЩiднавши отриманi точки отримуiмо графiк змiни кiнетичноi енергii ΔE= ƒ(φ).
2.5 Побудова графiка Jпр=ƒ(φ).
Проведемо розрахунок для першого положення механiзму.
Визначаiмо осьовий момент iнерцii ланок
![]()
![]() , так як довжина ℓ3 змiнюiться, тому для кожного положення його розраховуiмо окремо, а результати заносимо в таблицю № 4.
, так як довжина ℓ3 змiнюiться, тому для кожного положення його розраховуiмо окремо, а результати заносимо в таблицю № 4.
![]()
Визначаiмо швидкiсть центрiв мас ланок:
![]()
![]()
Аналогiчно швидкiсть центрiв мас ланок рахуiмо i для iнших положень механiзму, результати зараховуiмо в таблицю № 3.
Таблиця №3
Од. вимiр. | Положення механiзму | ||||||||
0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
Vs3 | м/с | 0 | 0,72 | 1,44 | 0 | 0,792 | 1,224 | 1,224 | 0,792 |
Vs4 | м/с | 0 | 0,72 | 1,44 | 0 | 0,72 | 1,008 | 1,008 | 0,72 |
Визначаiмо кiнетичну енергiю механiзму:
![]()
де: Е1 тАУ кiнетична енергiя ланки №1;
Е2 тАУ кiнетична енергiя ланки №2;
Е3 тАУ кiнетична енергiя ланки №3;
Е4 тАУ кiнетична енергiя ланки №4;
Е5 тАУ кiнетична енергiя ланки №5.
![]()
![]()
![]()
![]()
![]()
![]()
Визначаiмо приведений осьовий момент iнерцii:
![]()
Результати розрахункiв для iнших положень механiзму проводимо аналогiчно, а результати заносимо в таблицю №4.
Таблиця №4
Од. вимiр | Положення механiзму | ||||||||
0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
J3 | кгВ·м2 | 0,4752 | 0,,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 |
E1 | Дж | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 |
E2 | Дж | 0 | 1,34639 | 1,51323 | 0 | 0,74287 | 1,7936 | 1,7936 | 0,876 |
E3 | Дж | 0 | 0,88483 | 0,88422 | 0 | 0,22197 | 0,43224 | 0,37308 | 0,22257 |
E4 | Дж | 0 | 1,211096 | 1,630886 | 0 | 0,33696 | 0,66044 | 0,56946 | 0,33696 |
E5 | Дж | 1,9008 | 5,342626 | 5,929136 | 1,9008 | 3,2026 | 4,78208 | 4,63694 | 1,91073 |
Eмех | Дж | 0,000594 | 0,001669 | 0,001853 | 0,000594 | 0,001008 | 0,001496 | 0,001449 | 0,000597 |
Jпр | кгВ·м2 | 64 | 180 | 200 | 64 | 109 | 161 | 161 | 64 |
(Jпр)гр | мм | 0,004386 | 0,002984 | 0,002984 | 0,004386 | 0,006115 | 0,007278 | 0,007278 | 0,006115 |
Визначаiмо масштабний коефiцiiнт:
![]()
де: Y2 тАУ вiдстань на осi абсцис вiдповiдаюча даному осьовому моменту.
Перераховуiмо усi отриманi осьовi моменти iнерцii в графiчнi аналоги:
![]()
Будуiмо систему координат. По осi ординат вiдмiчаiмо кут повороту механiзму, а по осi абсцис на променях проведених з точок кута повороту проводимо графiчнi аналоги приведеного осьового моменту. ЗтАЩiднуiмо отриманi точки i отримуiмо графiк приведеного моменту Jпр=ƒ(φ).
2.6 Побудова дiаграми енергомас.
Будуiмо вiсь координат. До цiii вiсi проводимо променi з графiка приведеного осьового моменту Jпр=ƒ(φ) i змiни кiнетичноi енергii ΔЕ=ƒ(φ). На перетинi вiдповiдних променiв отримуiмо точки зтАЩiднавши якi, отримуiмо дiаграму енергомас (петля Вiттенбауера).
3. Проектування профiлю кулачкового механiзму.
3.1 Вихiднi даннi.
 Схема кулачкового механiзму (мал. 4)
Схема кулачкового механiзму (мал. 4)
![]() ω
ω
мал. 6).
φп тАУ 90˚ (фаза пiдьому штовхача);
φс тАУ 30˚ (фаза далекого стояння);
φо - 160˚ (фаза спускання);
ω тАУ 85 1/С (кутова швидкiсть);
δ - 35˚ (кут тиску);
h тАУ 30 мм (хiд штовхача).
Аналог прискорення

φ
φп φс φо
мал. 7).
3.2 Визначення закону руху штовхача.
Будуiмо графiчний аналог прискорення штовхача ![]() . По осi ординат вiдкладаiмо аналог прискорення
. По осi ординат вiдкладаiмо аналог прискорення ![]() , а по вiсi абсцис кут повороту φ.
, а по вiсi абсцис кут повороту φ.
Визначаiмо масштабний коефiцiiнт по вiсi абсцис:
![]()
де: Х тАУ довiльний вiдрiзок вздовж вiсi абсцис.
Цей вiдрiзок розбиваiмо на три дiлянки Хп, Хс та Хо, пропорцiйно кутам повороту φп, φс, φо. Вiдрiзки Хп та Хо розбиваiмо на вiсiм рiвних частин. На вiдрiзку Хп , задаiмося амплiтудою Yп=95 мм.
Визначаiмо амплiтуду на вiдрiзку Хn:

Згiдно вихiдних даних будуiмо графiчний аналог прискорення ![]() .
.
Визначаiмо мiжполюсну вiдстань:
![]()
Методом графiчного iнтегрування графiчного аналога прискорень отримуiмо графiчний аналог швидкостi.
![]() графiчний аналог швидкостi.
графiчний аналог швидкостi.
Методом графiчного iнтегрування графiчного аналога швидкостi отримуiмо графiчний аналог перемiщень ![]() .
.
Визначаiмо масштабний коефiцiiнт:
![]()
Визначаiмо дiйснi значення перемiщень штовхача:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
де: Si тАУ перемiщення штовхача.
3.3 Знаходження мiнiмального радiуса кулачка.
Будуiмо залежнiсть аналога швидкостi вiд перемiщення штовхача ![]() .
.
Визначаiмо масштабний коефiцiiнт:
![]()
Перераховуiмо дiйсне перемiщення штовхача в графiчний аналог:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На ординатi вiдкладаiмо перемiщення штовхача (графiчне), а на осi абсцис вiдкладаiмо вiдрiзки Х, якi знаходимо за формулою:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ОбтАЩiднуiмо отриманi точки кривою, через кiнцi найбiльших вiдрiзкiв проводимо вертикальнi лiнii, до них проводимо променi пiд кутом δ дотичними до графiка ƒ(φ)=dS/dφ
Перетин лiнiй кутiв δ i точка О1 i i центром маси кулачка. Вiдстань О1О i мiнiмальним радiусом кулачка.
![]()
Вiдстань точки О1 по горизонталi вiд осi ординат i ексцентриситетом.
![]()
3.4 Проектування профiлю кулачка.
З точки О1 проводимо кола rmin, rmin+ih. На вiдстанi е вiд точки О1 проводимо вертикаль, на нiй вiдкладаiмо вiдрiзки перемiщення штовхача. Проводимо вертикаль з точки О1, вiд якоi вiдкладаiмо кути φп,φс,φо, в сторону протилежну ω. Кути φБ i φА дiлимо на вiсiм рiвних частин, отримуiмо точки 0÷17. З цих точок проводимо променi дотичнi до кола радiуса е. З точок 0÷17 вiдкладених на вертикалi проводимо концентричнi кола до перетину з вiдповiдними дотичними точками. На iх перетинi отримуiмо точки 0тАЩ÷17тАЩ. Об,iднуiмо iх плавною лiнiiю i отримуiмо теоретичний профiль кулачка.
Визначаiмо радiус ролика кулачка:
![]()
Використовуючи теоретичний профiль кулачка як геометричне мiсце точок центрiв ролика проводимо рiд кiл радiусом rP.
Робочiй профiль будуiмо дотичною лiнiiю до кiл радiусом rP.
4. Проектування зубчатого зачеплення.
4.1 Вихiднi даннi.
m - 3 (модуль зачеплення);
Y - 0.6 (коефiцiiнт сприйнятого змiщення);
![]() (кiлькiсть зубцiв).
(кiлькiсть зубцiв).
4.2 Визначення розмiрiв геометричних параметрiв.
Визначаiмо радiуси дiлильних кiл:
![]()
![]()
Визначаiмо крок зачеплення:
![]()
Визначимо радiуси основних кiл:
![]()
![]()
де: α=20В°
Визначаiмо мiжосьову вiдстань:
![]()
![]()
Визначимо кут зачеплення:
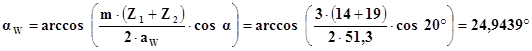
Визначаiмо радiуси початкових кiл:
![]()
![]()
Визначаiмо коефiцiiнт змiщення:
![]()
![]()
![]()
Визначаiмо коефiцiiнт змiщення iнструмента на шестернi:

![]()
Визначаiмо радiуси кола западин:
![]()
![]()
де: ha*=1; C*=0,25.
Визначаiмо радiуси кола виступiв:
![]()
![]()
Визначаiмо ширину зубцiв по дiлильному колу:
![]()
![]()
Визначаiмо висоту нiжки зубця:
![]()
Визначаiмо висоту зубця:
![]()
Перевiрка:
![]()
![]()
![]()
4.3 Проектування зачеплення.
Приймаiмо висоту зубця на кресленнi №4 тАУ 50 мм.
Визначимо масштабний коефiцiiнт:
![]()
Визначимо графiчнi розмiри геометричних параметрiв:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На кресленнi №4 проводимо мiжосьову вiдстань ![]() i отримуiмо центри колiс, точки О1 та О2 , з яких проводимо кола радiусами
i отримуiмо центри колiс, точки О1 та О2 , з яких проводимо кола радiусами ![]() . Проводимо загальну дотичну до основних кiл. Вiдмiчаiмо точки дотику А та В. Визначаiмо теоретичну лiнiю зачеплення АВ. Проводимо початковi кола
. Проводимо загальну дотичну до основних кiл. Вiдмiчаiмо точки дотику А та В. Визначаiмо теоретичну лiнiю зачеплення АВ. Проводимо початковi кола ![]() , вони повиннi перетнутися в точцi W, точцi перетину лiнii зачеплення i лiнii центрiв.
, вони повиннi перетнутися в точцi W, точцi перетину лiнii зачеплення i лiнii центрiв.
Проводимо кола радiусами ![]() . Вiдрiзок AW дiлимо на чотири частини i отримуiмо точки 1, 2, 3, 4, якi зносимо на коло
. Вiдрiзок AW дiлимо на чотири частини i отримуiмо точки 1, 2, 3, 4, якi зносимо на коло ![]() i отримуiмо точки 1тАЩ,2тАЩ,3тАЩ,4тАЩ, з яких проводимо дотичнi до кола i зносимо на вiдповiднi дотичнi вiдрiзки W0, W1, W2, W3, W4 . ЗтАЩiднуiмо точки i отримуiмо профiль зубця. Проводимо вiсь симетрii S1/2 i по закону симетрii добудовуiмо iншу сторону зубця. Потiм округлюiмо зубець радiусом округлення ρ. Аналогiчно будуiмо зубець i для другого колеса. Робимо шаблони i добудовуiмо ще по два зубця.
i отримуiмо точки 1тАЩ,2тАЩ,3тАЩ,4тАЩ, з яких проводимо дотичнi до кола i зносимо на вiдповiднi дотичнi вiдрiзки W0, W1, W2, W3, W4 . ЗтАЩiднуiмо точки i отримуiмо профiль зубця. Проводимо вiсь симетрii S1/2 i по закону симетрii добудовуiмо iншу сторону зубця. Потiм округлюiмо зубець радiусом округлення ρ. Аналогiчно будуiмо зубець i для другого колеса. Робимо шаблони i добудовуiмо ще по два зубця.
4.4 Визначаiмо величини параметрiв якостi.
Визначаiмо коефiцiiнт перекриття:
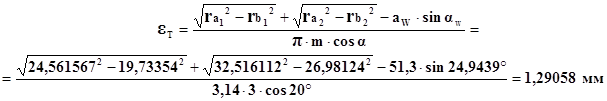
![]()
де: ab тАУ практична лiнiя зачеплення
Визначимо коефiцiiнти вiдносного ковзання:

де: Х тАУ вiдстань вiд точки А до точки зачеплення
UВместе с этим смотрят:
11-этажный жилой дом с мансардой
14-этажный 84-квартирный жилой дом
16-этажный жилой дом с монолитным каркасом в г. Краснодаре
180-квартирный жилой дом в г. Тихорецке
2-этажный 3-секционный 18-квартирный жилой дом в г. Мирном