Метрология

Метод приведения Он используется для определения результаВнтов косвенного измерения и его погрешности при наличии корреляВнции между погрешностями измерений аргументов. Метод можно также применять при неизвестных распределениях погрешностей аргументов. Он предполагает наличие ряда согласованных результаВнтов измерений аргументов Q₁₁,Q,₁₂,тАж,Q_1m; Q₂₁, Q₂₂, тАж, Q_2m; тАж, Q_j1, Q_J2, тАж, Q_jm; тАж; Q_L1, Q_{L2, тАж,} Q_Lm, полученных в процессе многократВнных измерений. Согласованность результатов измерений означает либо одновременное их осуществление, либо то, что они выполнены над одним и тем же объектом и в одних и тех же условиях.

Метод основан на приведении отдельных значений косвенно измеВнряемой величины к ряду простых измерений. Получаемые сочетания отдельных аргументов подставляют в формулу (8.6) и вычисляют отдельные значения измеряемой величины Q: Q₁, Q₂, .., Q_j, ,Q_L.

Результат косвенного измерения 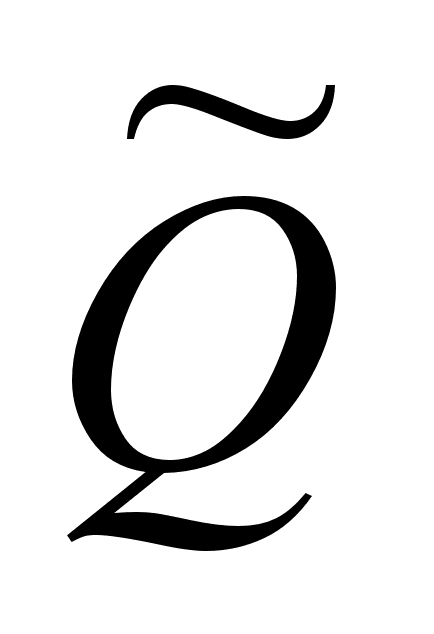и СКО его случайной поВнгрешности вычисляются по формулам

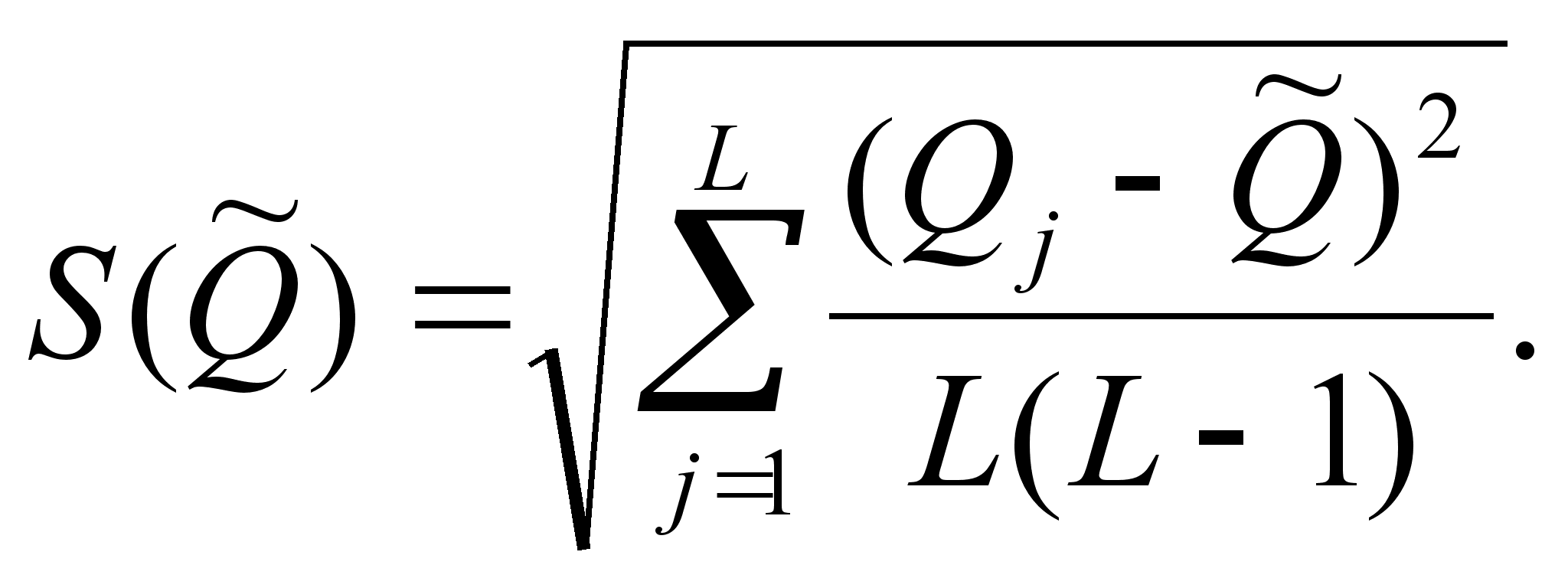
Доверительные границы случайной погрешности результата изВнмерения рассчитываются по формуле где Т - коэффиВнциент, зависящий от вида распределения отдельных значений опВнределяемой величины и выбранной доверительной вероятности. При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей выВнчисляются по методике для прямых многократных измерений, изВнложенной в ГОСТ 8.207-76.

Границы неисключенной систематической погрешности и доВнверительные границы погрешности результата косвенного измереВнния определяются так же, как и в рассмотренных выше случаях.

Глава 12. МЕТРОЛОГИЧЕСКИЕ

ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ И ИХ

НОРМИРОВАНИЕ

При использовании СИ принципиально важно знать степень соответствия информации о измеряемой величине, содержащейся в выходном сигнале, ее истинному значению. С этой целью для кажВндого СИ вводятся и нормируются определенные метрологические характеристики (MX). Метрологические характеристики тАФ это характеристики свойств средства измерений, оказывающие влияВнние на результат измерения и его погрешности. Характеристики, устанавливаемые нормативно-техническими документами, называВнются нормируемыми, а определяемые экспериментально тАФ действиВнтельными. Номенклатура MX, правила выбора комплексов нормиВнруемых MX для средств измерений и способы их нормирования определяются стандартом ГОСТ 8.009-84 "ГСИ. Нормируемые метВнрологические характеристики средств измерений". Подробные комВнментарии к этому документу приведены в [58].

Метрологические характеристики СИ позволяют:

тАв определять результаты измерений и рассчитывать оценки хаВнрактеристик инструментальной составляющей погрешности измеВнрения в реальных условиях применения СИ;

тАв рассчитывать MX каналов измерительных систем, состоящих из ряда средств измерений с известными MX;

тАв производить оптимальный выбор СИ, обеспечивающих требуеВнмое качество измерений при известных условиях их применения;

тАв сравнивать СИ различных типов с учетом условий применеВнния.

При разработке принципов выбора и нормирования средств изВнмерений необходимо придерживаться ряда положений, изложенВнных ниже.

1. Основным условием возможности решения всех перечисленВнных задач является наличие однозначной связи между нормироВнванными MX и инструментальными погрешностями. Эта связь устанавливается посредством математической модели инструментальной составляющей погрешности, в которой нормируемые MX должВнны быть аргументами. При этом важно, чтобы номенклатура MX и способы их выражения были оптимальны. Опыт эксплуатации разВнличных СИ показывает, что целесообразно нормировать комплекс MX, который, с одной стороны, не должен быть очень большим, а с другой тАФ каждая нормируемая MX должна отражать конкретные свойства СИ и при необходимости может быть проконтролирована.

2. Нормирование MX средств измерений должно производиться исходя из единых теоретических предпосылок. Это связано с тем, что в измерительных процессах могут участвовать СИ, построенВнные на различных принципах.

3. Нормируемые MX должны быть выражены в такой форме, чтобы с их помощью можно было обоснованно решать практически любые измерительные задачи и одновременно достаточно просто проводить контроль СИ на соответствие этим характеристикам.

4. Нормируемые MX должны обеспечивать возможность статиВнстического объединения, суммирования составляющих инструменВнтальной погрешности измерений. В общем случае она может быть определена как сумма (объединение) следующих составляющих погрешности:

тАв 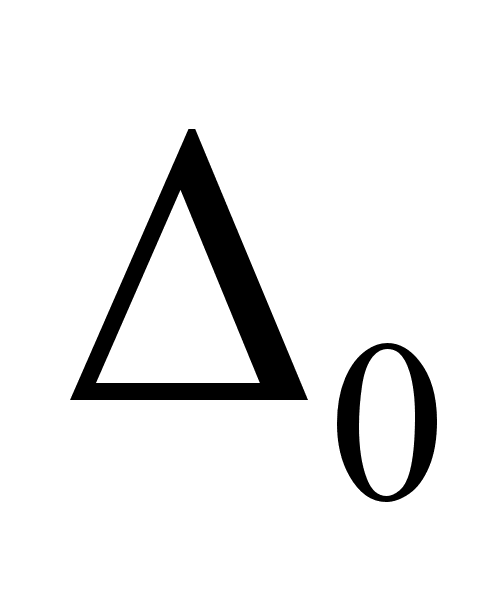(t), обусловленной отличием действительной функции преВнобразования в нормальных условиях от номинальной, приписанВнной соответствующими документами данному типу СИ. Эта погрешВнность называется основной;

тАв , обусловленной реакцией СИ на изменение внешних влияюВнщих величин и неинформативных параметров входного сигнала относительно их номинальных значений. Эта погрешность называВнется дополнительной;

тАв обусловленной реакцией СИ на скорость (частоту) измеВннения входного сигнала. Эта составляющая, называемая динамичеВнской погрешностью, зависит и от динамических свойств средств измерений, и от частотного спектра входного сигнала;

тАв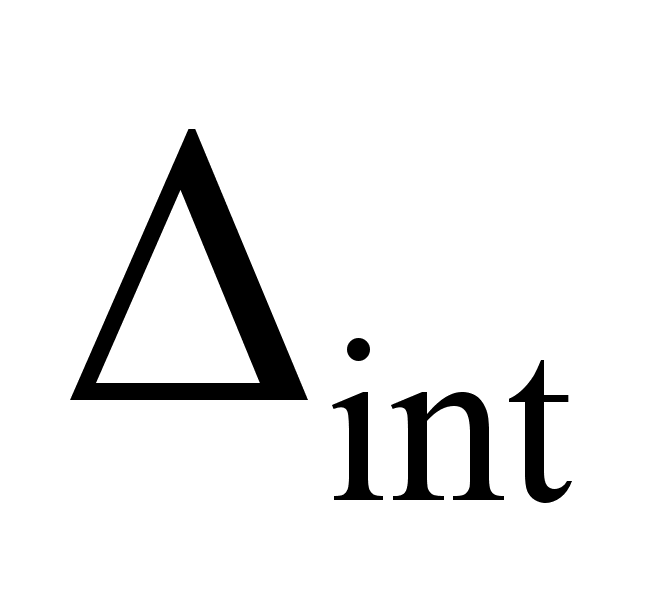, обусловленной взаимодействием СИ с объектом измереВнний или с другими СИ, включенным последовательно с ним в измеВнрительную систему. Эта погрешность зависит от характеристик и параметров входной цепи СИ и выходной цепи объекта измерений.

Таким образом, инструментальную составляющую погрешности СИ можно представить в виде

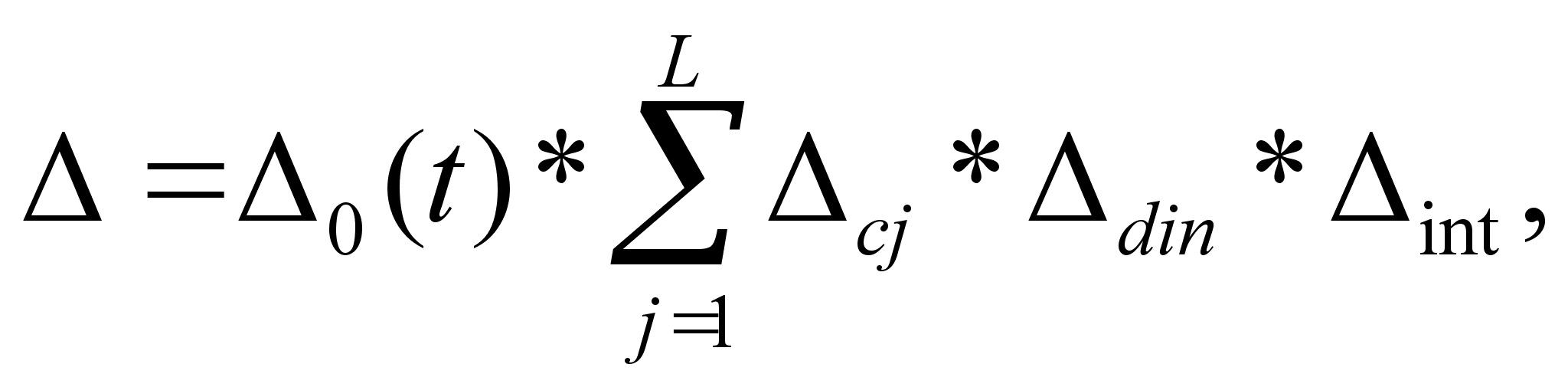
где * тАФ символ статистического объединения составляющих.

Первые две составляющие представляют собой статическую поВнгрешность СИ, а третья тАФ динамическую. Из них только основная погрешность определяется свойствами СИ. Дополнительная и диВннамическая погрешности зависят как от свойств самого СИ, так и от некоторых других причин (внешних условий, параметров измеВнрительного сигнала и др.).

Требования к универсальности и простоте статистического объВнединения составляющих инструментальной погрешности обуславВнливают необходимость их статистической независимости тАФ некорВнрелированности. Однако предположение о независимости этих составляющих не всегда верно.

Выделение динамической погрешности СИ как суммируемой составляющей допустимо только в частном, но весьма распростраВнненном случае, когда СИ можно считать линейным динамическим звеном и когда погрешность является весьма малой величиной по сравнению с выходным сигналом. Динамическое звено считается линейным, если оно описывается линейными дифференциальными уравнениями с постоянными коэффициентами. Для СИ, являющихся существенно нелинейными звеньями, выделение в отдельно суммиВнруемые составляющие статической и динамической погрешностей недопустимо.

5. Нормируемые MX должны быть инвариантны к условиям применения и режиму работы СИ и отражать только его свойства. Выбор MX необходимо осуществлять так, чтобы пользователь имел возможность рассчитывать по ним характеристики СИ в реальных условиях эксплуатации.

6. Нормируемые MX, приводимые в нормативно-технической документации, отражают свойства не отдельно взятого экземпляра СИ, а всей совокупности СИ данного типа, т.е. являются номиВннальными. Под типом понимается совокупность СИ, имеющих одиВннаковое назначение, схему и конструкцию и удовлетворяющих одВнним и тем же требованиям, регламентированным в технических условиях. Метрологические характеристики отдельного СИ данноВнго типа могут быть любыми в пределах области значений номиВннальных MX. Отсюда следует, что MX средства измерений данного

типа должна описываться как нестационарный случайный процесс. Математически строгий учет данного обстоятельства требует норВнмирования не только пределов MX как случайных величин, но и их временной зависимости (т.е. автокорреляционных функций). Это приведет к чрезвычайно сложной системе нормирования и практиВнческой невозможности контроля MX, поскольку при этом он долВнжен был бы осуществляться в строго определенные промежутки времени. Вследствие этого принята упрощенная система нормироВнвания, предусматривающая разумный компромисс между матемаВнтической строгостью и необходимой практической простотой. В принятой системе низкочастотные изменения случайных составляюВнщих погрешности, период которых соизмерим с длительностью межВнповерочного интервала, при нормировании MX не учитываются. Они определяют показатели надежности СИ, обуславливают выбор рациональных межповерочных интервалов и других аналогичных характеристик. Высокочастотные изменения случайных составляюВнщих погрешности, интервалы корреляции которых соизмеримы с длительностью процесса измерения, необходимо учитывать путем нормирования, например, их автокорреляционых функций.

Перечень нормируемых MX делится на шесть основных групп

(рис.12.1), которые и рассматриваются далее.

3.2. КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЯ

Для обеспечения единства измерений и взаимозаменяемости средств измерений характеристики их метрологических свойств (метрологические характеристики) нормируются и регламентируются стандартами. НоменкВнлатура метрологических характеристик и полнота, с которой они должны описывать те или иные свойства средств измерений, зависят от назначения средств измерений, условий эксплуатации, режима работы и многих друВнгих факторов. В полном перечне метрологических характеристик можно выделить следующие их группы:

- градуировочные характеристики, определяющие соотношение меВнжду сигналами на входе и выходе средства измерений в статическом реВнжиме. К ним относятся, например, номинальная статическая характериВнстика преобразования (градуировочная характеристика) прибора, ноВнминальное значение меры, пределы измерения, цена деления шкалы, вид и параметры цифрового кода в цифровом приборе;

- показатели точности средства измерения, позволяющие оценить инструментальную составляющую погрешности результата измереВнния;

- динамические характеристики, отражающие инерционные свойстВнва средств измерения и необходимые для оценивания динамических поВнгрешностей измерений;

- функции влияния, отражающие зависимость метрологических хаВнрактеристик средств измерения от воздействия влияющих величин или неинформативных параметров входного сигнала.

Неинформативным называется параметр входного сигнала, не свяВнзанный непосредственно с измеряемой величиной, но оказывающий влияние на результат измерения, например, частота переменного элекВнтрического тока при измерении его амплитуды.

Обычно метрологические характеристики нормируются раздельно для нормальных и рабочих условий применения средств измерений. НормальВнными считаются такие условия, при которых изменением метрологических характеристик под воздействием влияющих величин можно пренебречь. Так, для многих типов средств измерений нормальными условиями примеВннения являются: температура (20В±5)В°С, атмосферное давление 84.. 106 кПа, относительная влажность 30.. 80%. Рабочие условия отличаются от норВнмальных более широкими диапазонами влияющих величин.

Учет всех нормируемых метрологических характеристик средства измерений при оценивании погрешности результата измерений, как видВнно, сложная и трудоемкая процедура, оправданная при измерениях поВнвышенной точности. При измерениях на производстве, в обиходе такая точность не всегда нужна. В то же время, определенная информация о возможной инструментальной составляющей погрешности измерения необходима. Такая информация дается указанием класса точности средВнства измерений.

Под классом точности понимают обобщенную характеристику точности средств измерений данного типа, определяемую пределами доВнпускаемой основной погрешности. Классы точности присваивают средВнствам измерений при их разработке на основании исследований и испыВнтаний представительной партии средств измерения данного типа. При этом пределы допускаемых погрешностей нормируют и выражают в форме абсолютных, приведенных или относительных погрешностей, в зависимости от характера изменения погрешностей в пределах диапазоВнна измерений. Приведенной называется относительная погрешность, вычисленная в процентах от некоторого нормирующего значения. В качестве нормирующего обычно принимается конечное значение шкалы (верхний предел измерения для приборов с односторонней шкалой или сумма пределов тАФ для приборов с нулем посредине).

Пределы допускаемой абсолютной погрешности устанавливают по формулам:

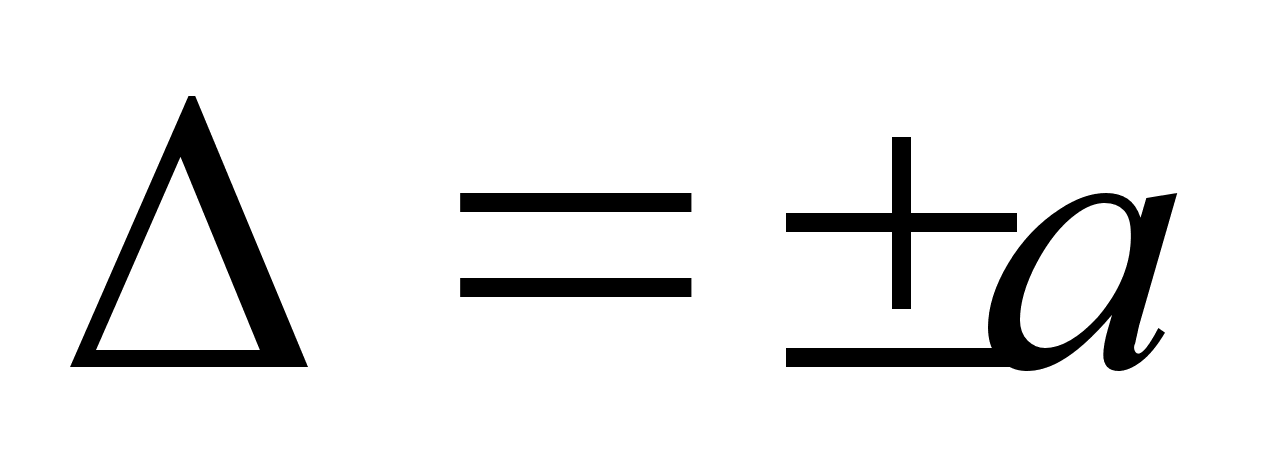
(3.4)

или

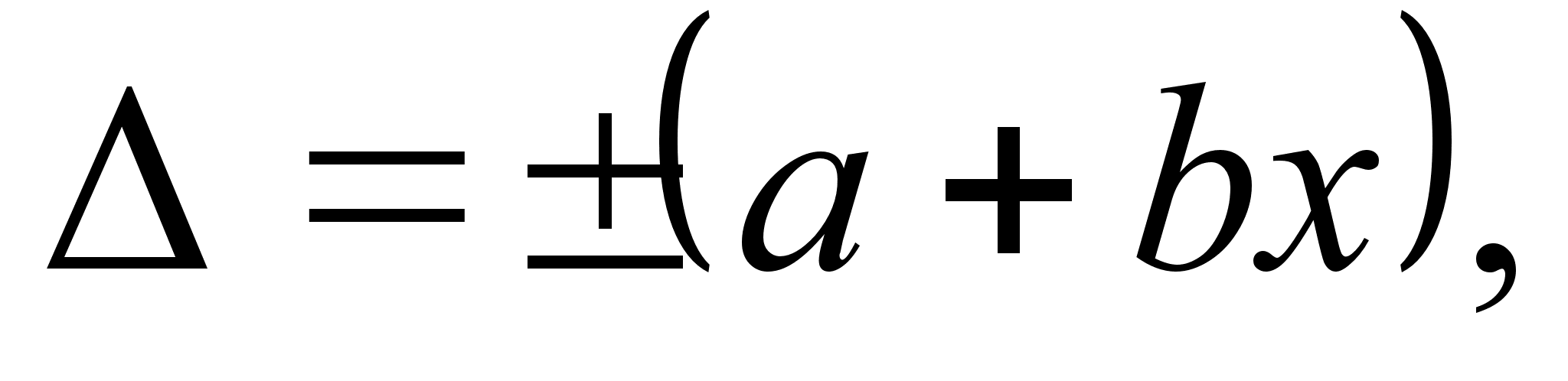
где х тАФ значение измеряемой величины; а, b положительные числа, не зависящие от х.

положительные числа, не

Нормирование в соответствии с (3.5) означает, что в составе поВнгрешности средства измерения присутствуют аддитивная и мультиплиВнкативная составляющие, например, для генератора низкой частоты ГЗ-36 = В±(0,03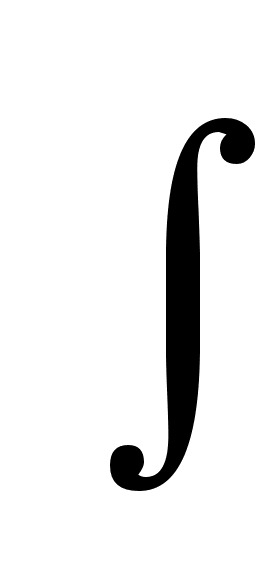+2) Гц.

Пределы допускаемой приведенной основной погрешности опредеВнляют по формуле

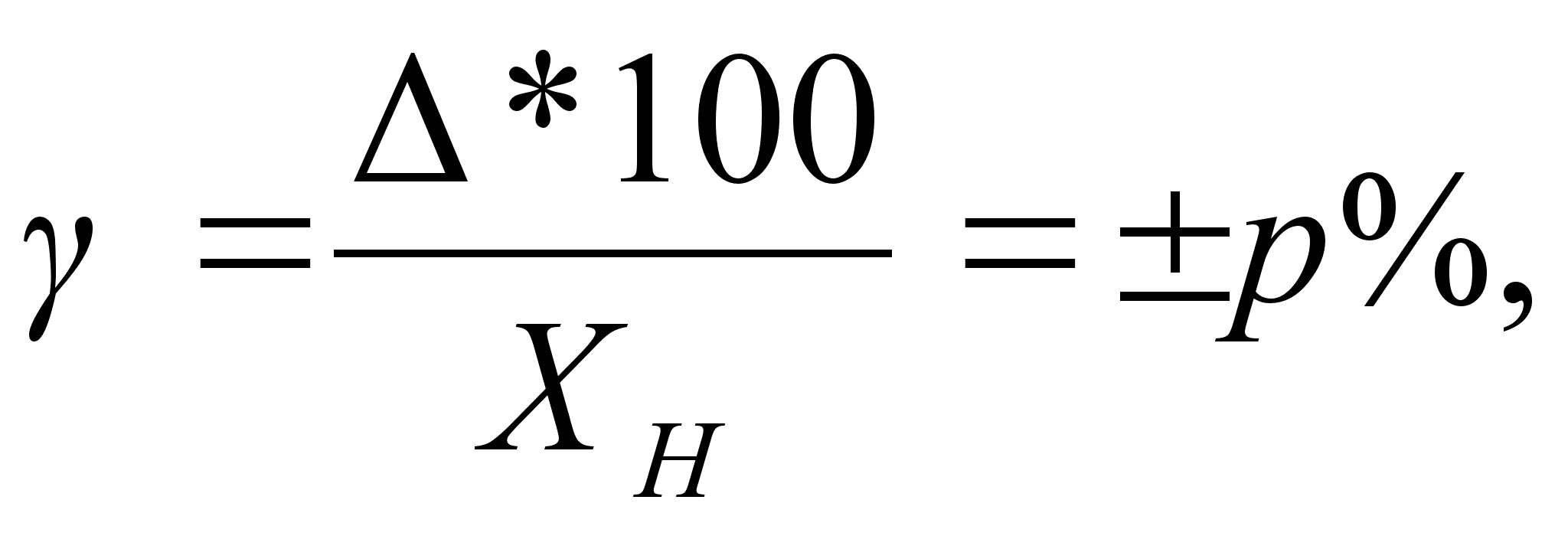
где Х_н тАФ нормирующее значение, выраженное в тех же единицах, что и х; р тАФ отвлеченное положительное число, выбираемое из стандартизоВнванного ряда значений (1*10ⁿ; 1,5*10ⁿ; ..,5*10ⁿ; ..,где n - 1,0,-1,-2 и т.д.).

Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным длине шкалы.

Пределы допускаемой относительной основной погрешности:

если установлена по формуле (3.4)

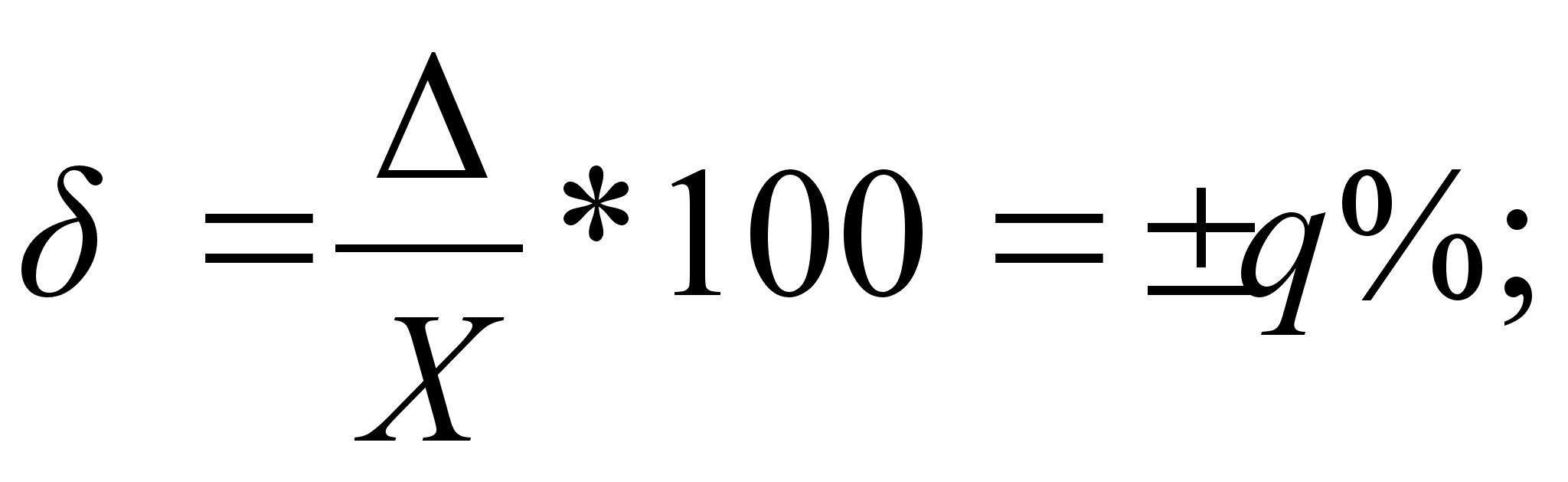
(3.7)

если А установлена по (3.5)

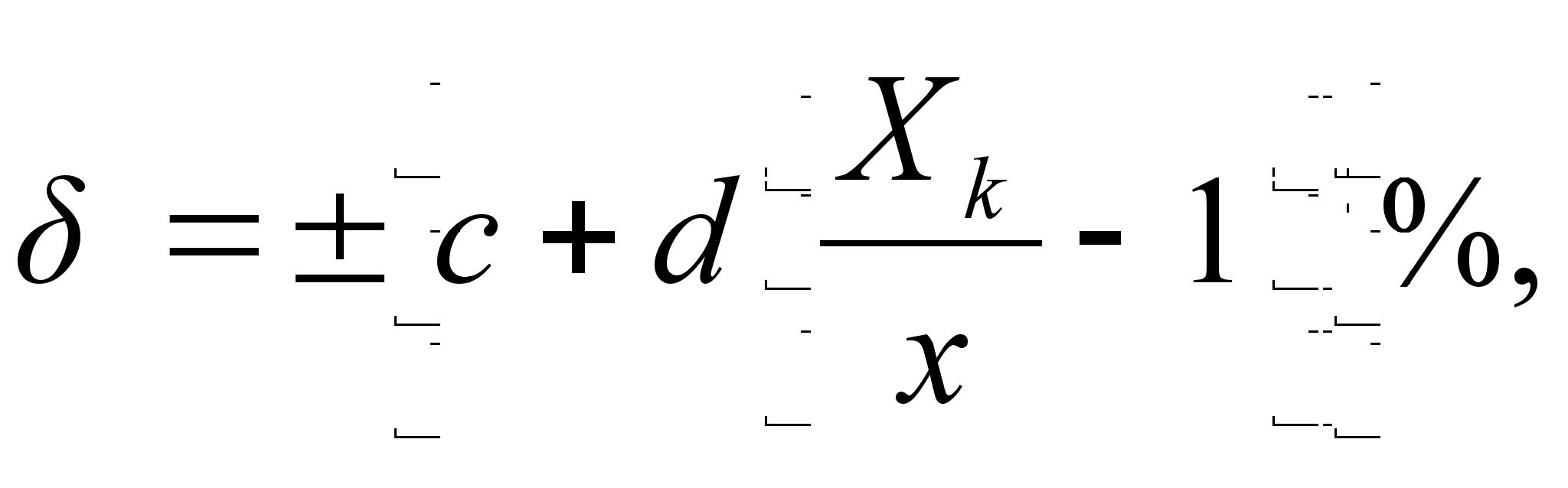
(3.8)

где q тАФ отвлеченное положительное число, выбираемое из стандартизоВнванного ряда значений; Х_к тАФ больший по модулю из пределов измереВнний (верхний предел измерения, или сумма пределов измерения для приВнборов с нулем посредине); с, d тАФ положительные числа, выбираемые из стандартизованного ряда; х тАФ показание прибора.

Пределы допускаемых дополнительных погрешностей, как правило, устанавливают в виде дольного значения предела допускаемой основной погрешности. Обозначение классов точности наносится на шкалы, щитВнки или корпуса приборов.

К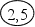лассы точности средств измерений обозначаются условными знаками (буквами, цифрами). Для средств измерений, пределы допускаемой основной погрешности которых выражают в форме приведенной погрешности или отВнносительной погрешности в соответствии с (3.6) и (3.7), классы точности обозначаются числами, равными этим пределам в процентах. Чтобы отВнличить относительную погрешность от приведенной, обозначение класса

точности в виде относительной погрешности обводят кружком . Если

п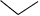огрешность нормирована в процентах от длины шкалы, то под обозначением класса ставится знак . Если погрешность нормирована форВнмулой (3.8), то класс точности обозначается как с/d (например, 0,02 / 0,01).

Пример. На шкале амперметра с пределами измерения 0.. 10 А нанесено обозначение класса точности 2,5. Это означает, что для данного прибора нормирована приведенная

погрешность. Подставляя в (3.6) Х_n = 10А и р = 2,5 получим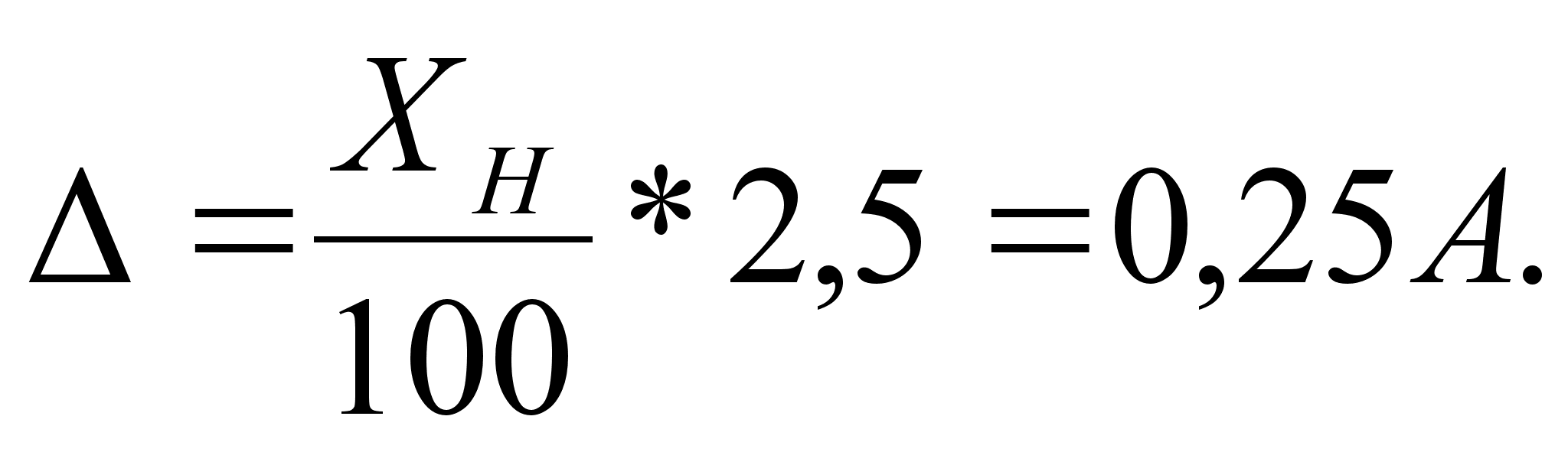

Если бы обозначение класса точности было , то погрешность следовало бы

вычислить в процентах от измеренного значения. Так, при I_изм = 2А, погрешность прибо

ра не должна превышать .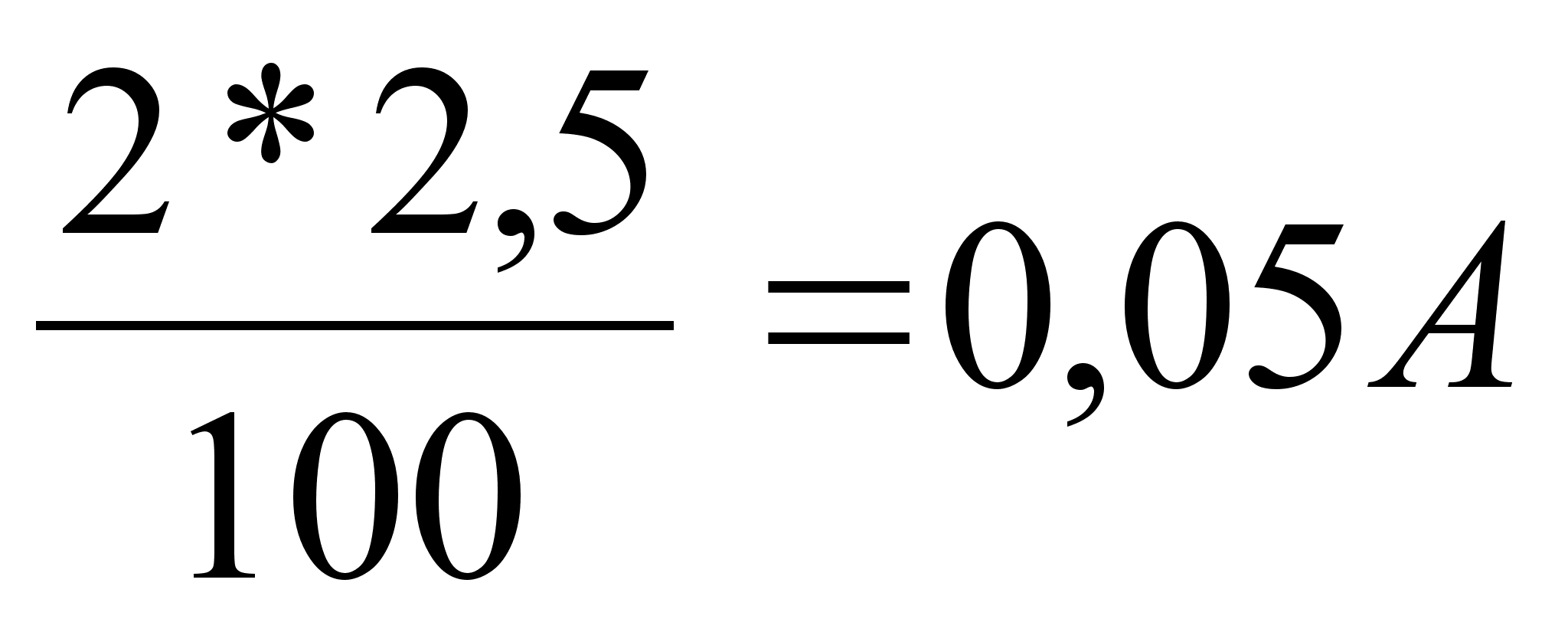

2.7. КОСВЕННЫЕ ИЗМЕРЕНИЯ

При косвенных измерениях искомое значение величины находят расчетом на основе измерения других величин, связанных с измеряемой величиной известной зависимостью

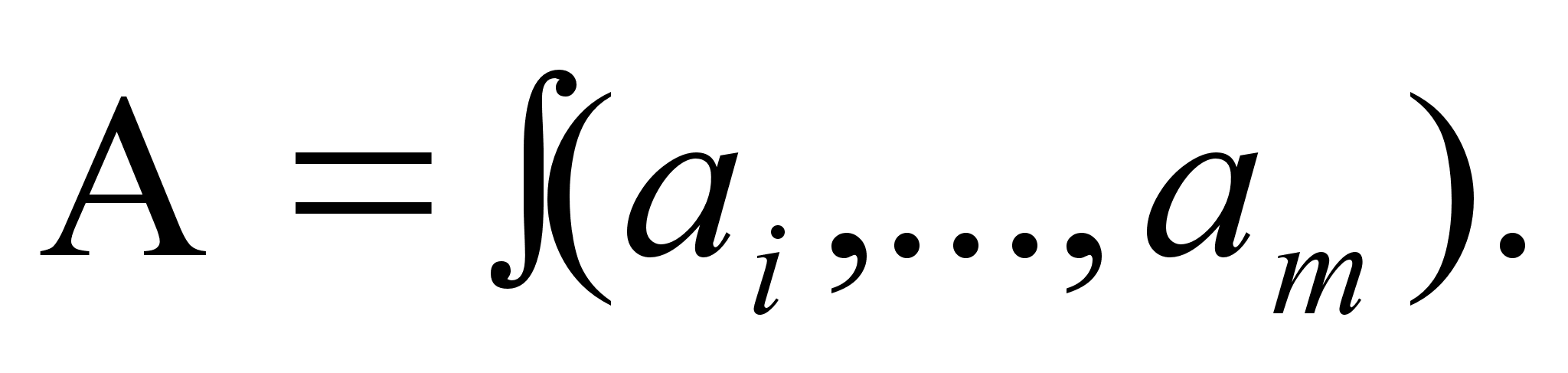
Результатом косвенного измерения является оценка величины А, коВнторую находят подстановкой в формулу (2.18) оценок аргументов а_i.

Поскольку каждый из аргументов а, измеряется с некоторой погрешВнностью, то задача оценивания погрешности результата сводится к сумВнмированию погрешностей измерения аргументов. Однако особенность косвенных измерений состоит в том, что вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функВнции (2. 18).

Для оценки погрешностей существенно разделение косвенных измеВнрений на линейные и нелинейные косвенные измерения. При линейных косвенныхизмерениях уравнение измерений имеет вид

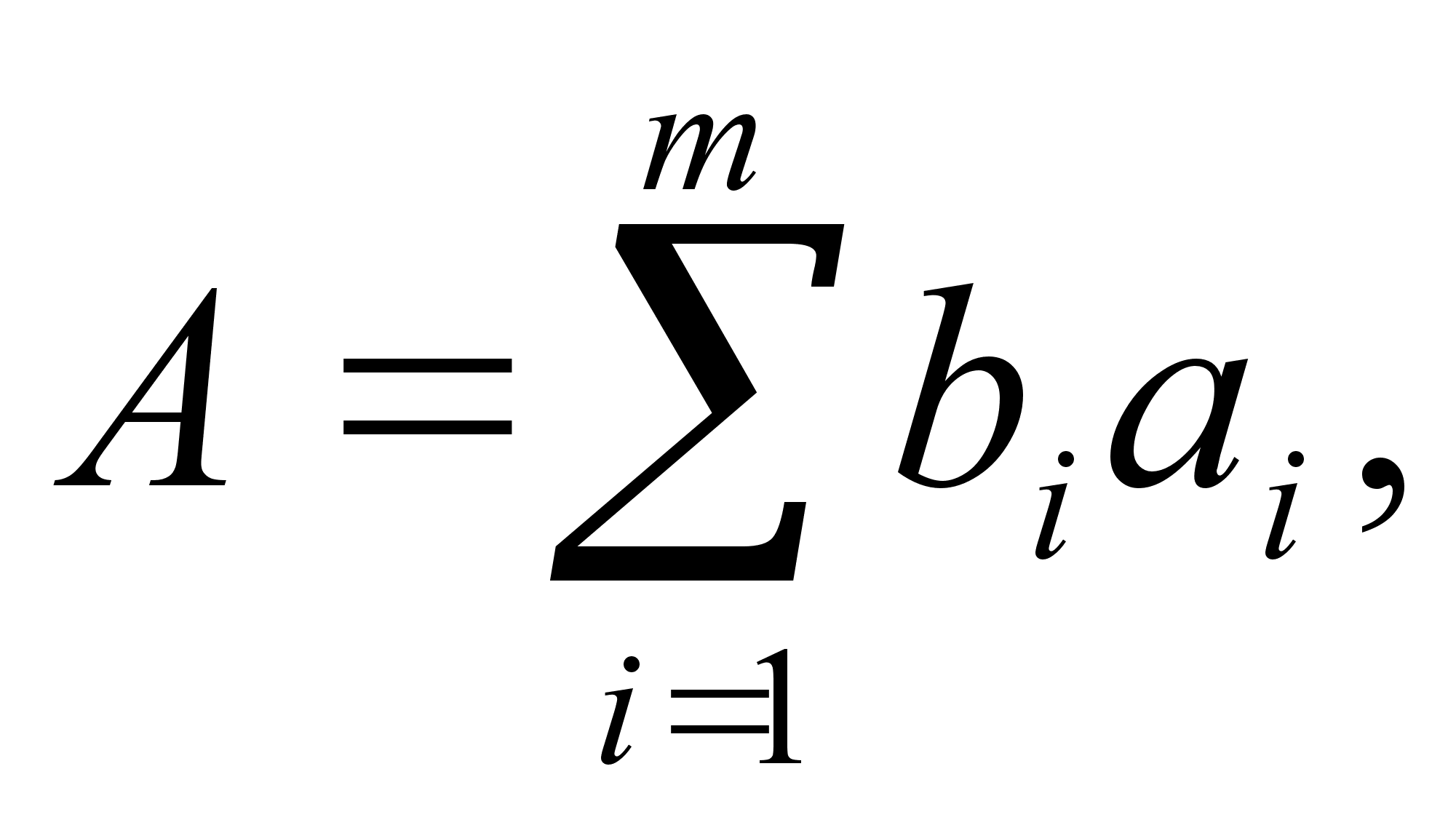
где b_jтАФ постоянные коэффициенты при аргументах а_i.

Любые другие функциональные зависимости (2.18) относятся к неВнлинейным косвенным измерениям.

Результат линейного косвенного измерения вычисляют по формуле (2.19), подставляя в нее измеренные значения аргументов.

Погрешности измерения аргументов могут быть заданы своими граВнницами , либо доверительными границами 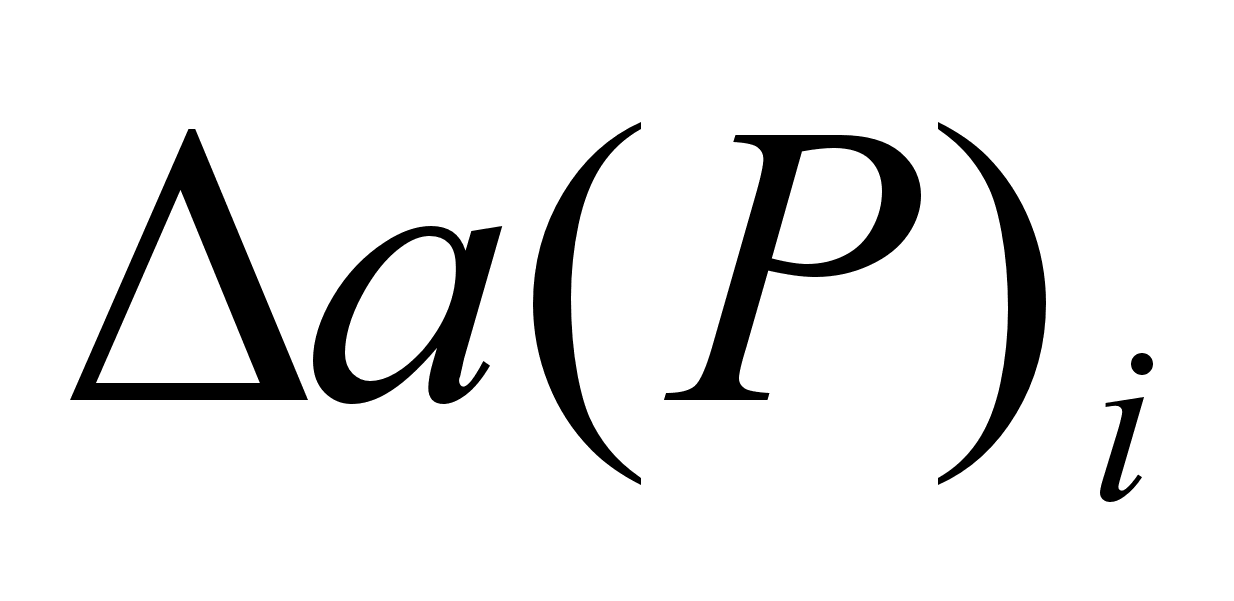, с доверительными вероятностями Р_i .

При малом числе аргументов (меньше пяти) простая оценка погрешВнности результата 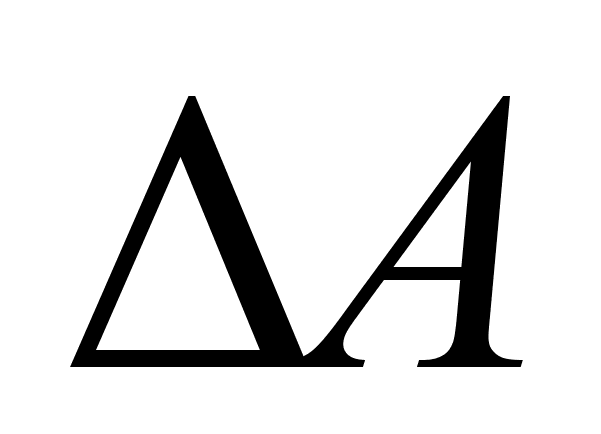получается суммированием предельных погрешноВнстей (без учета знака), т.е. подстановкой границ 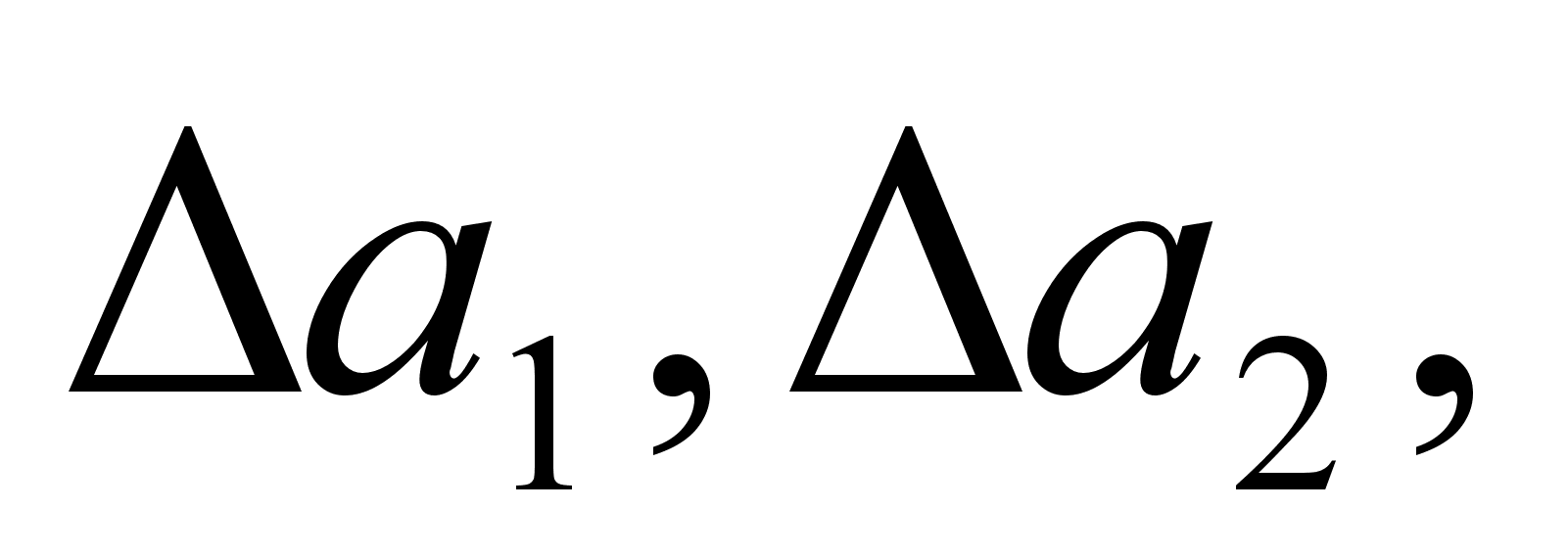.. , 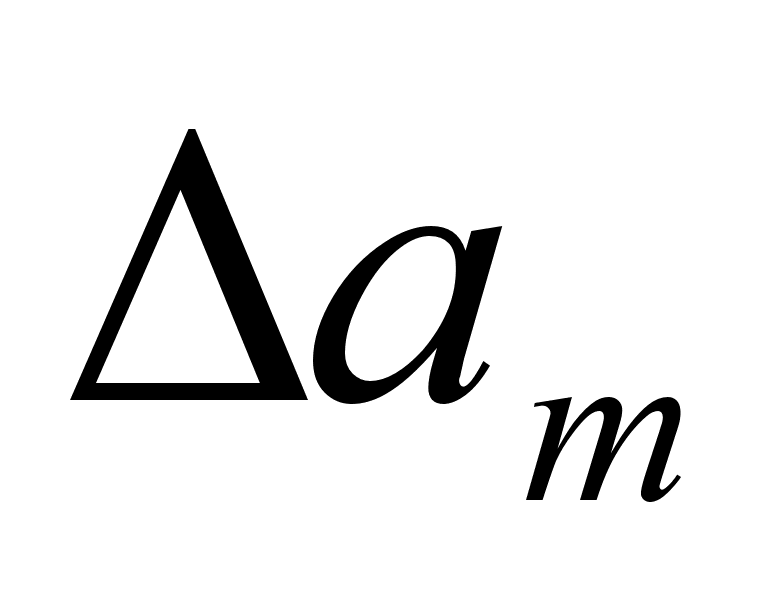в выВнражение

(2.20)

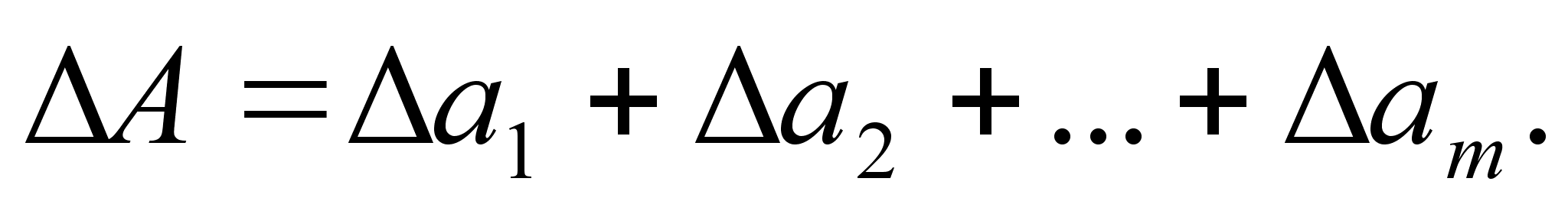
Однако эта оценка является излишне завышенной, поскольку таВнкое суммирование фактически означает, что погрешности измерения всех аргументов одновременно имеют максимальное значение и совВнпадают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к стаВнтистическому суммированию погрешностей аргументов. Полагая, что в заданных границах погрешности аргументов распределены равномерно, доверительные границы 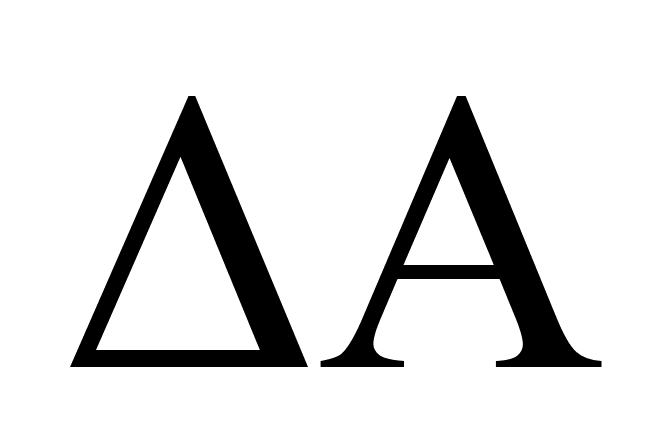(Р) погрешности результата измерения рассчитывают по формуле

(2.21)

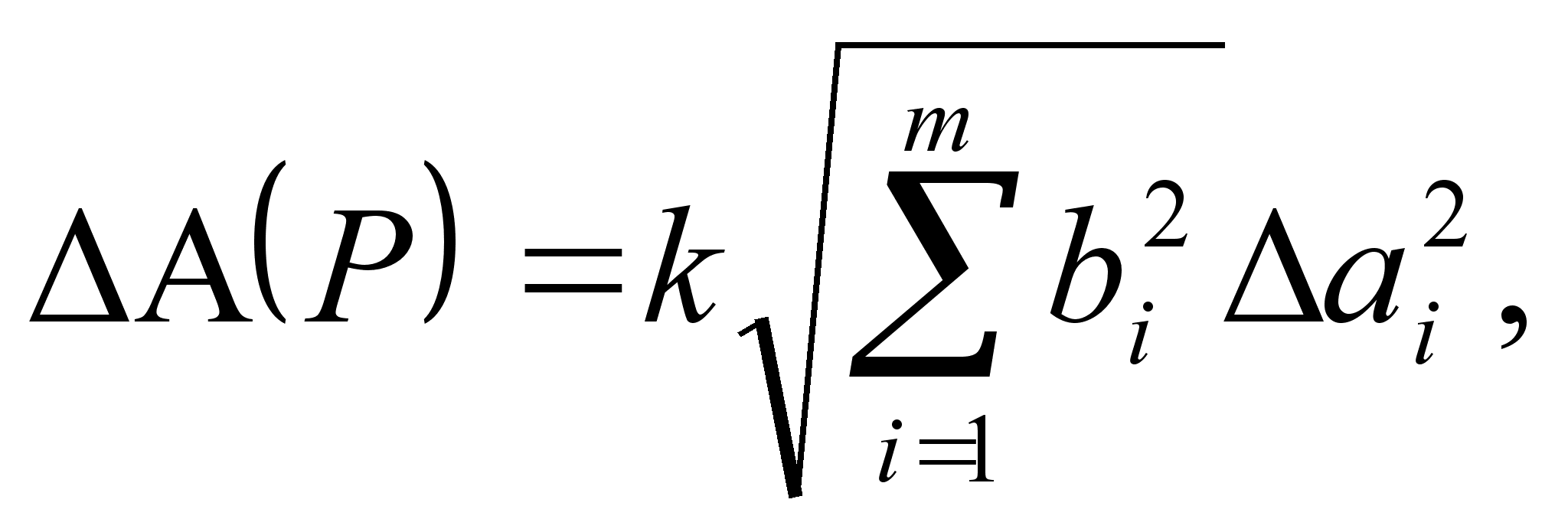
где коэффициент k определен в (2.15).

Если погрешности измерения аргументов заданы доверительныВнми границами с одинаковыми доверительными вероятностями, то полагая распределение этих погрешностей нормальным, доверительВнные границы результата находят по формуле

(2.22)

При различных доверительных вероятностях погрешностей аргуменВнтов их необходимо привести к одному и тому же значению Р.

Нелинейные косвенные измерения характеризуВнются тем, что результаты измерений аргументов подвергаются функциоВннальным преобразованиям. Но, как показано в теории вероятностей, любые, даже простейшие функциональные преобразования случайных величин, приводят к изменению законов их распределения.

Пример. Результат измерения аргумента подчиняется нормальному распределению плотности вероятностей, кривая которого 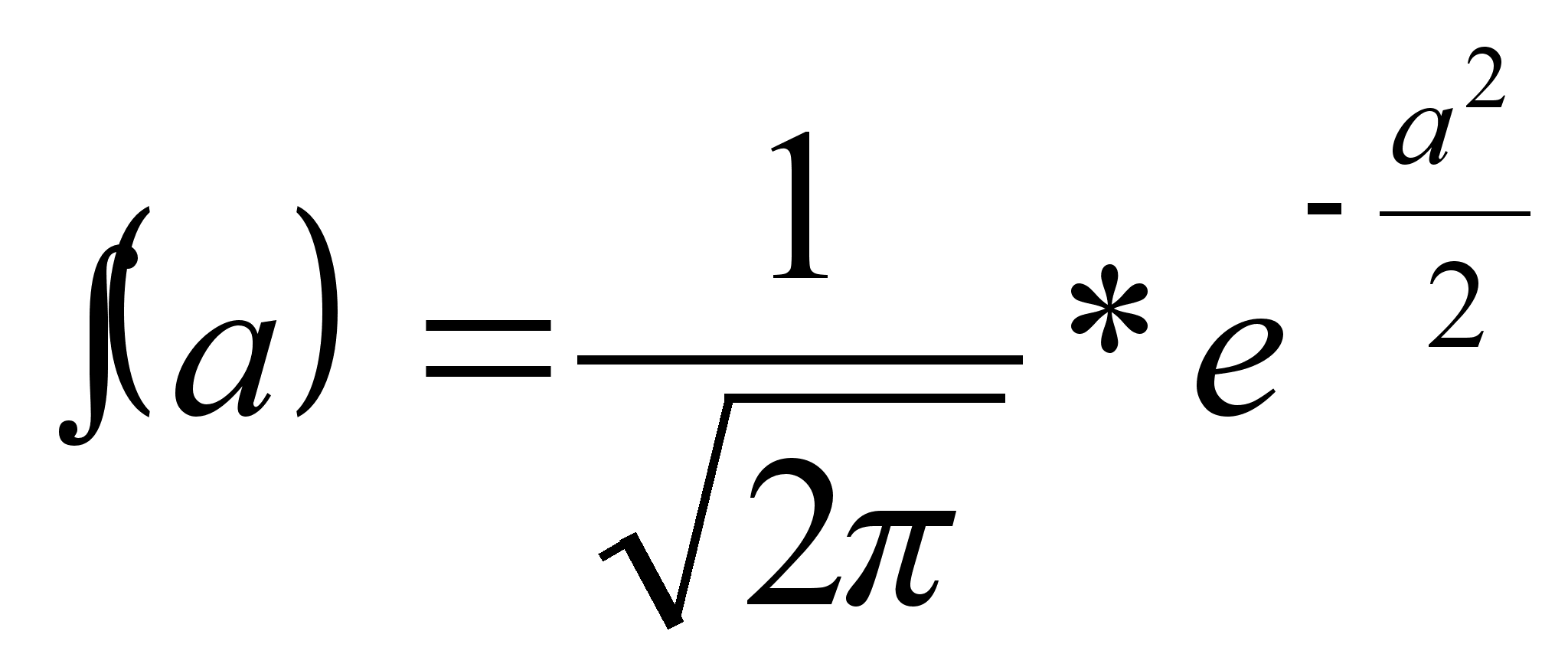показана на рис. 2.13, а.

При возведении измеренного значения величины в квадрат q = а² график плотности распределения претерпевает изменения и принимает вид, показанный на рис. 2.13, б (выВнвод формулы опускаем). Уравнение кривой в этом случае имеет следующий вид:

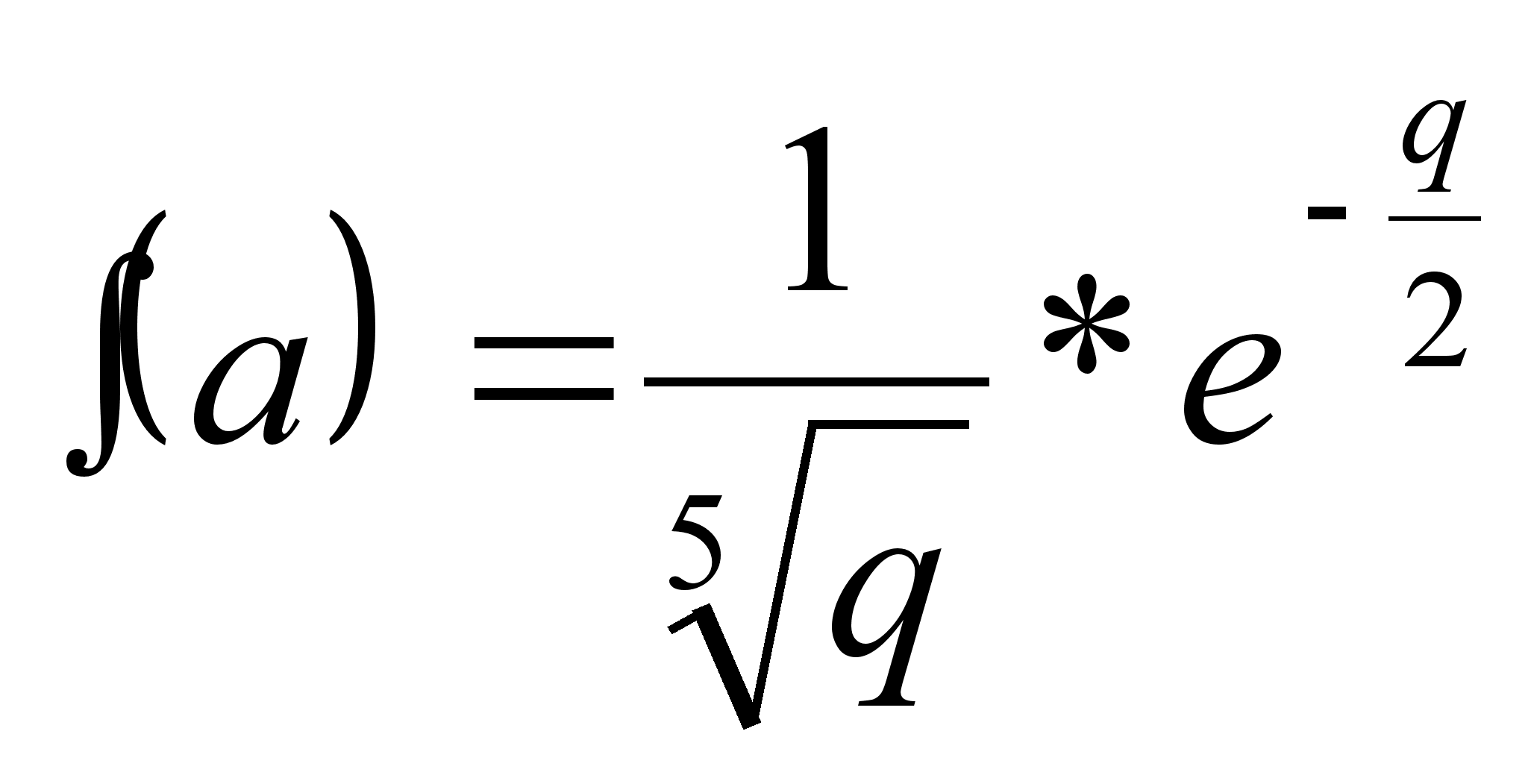
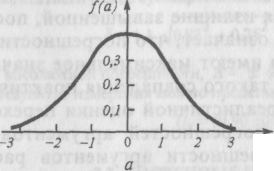
Рис. 2.13. Графики плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, и квадрата этого результата измерения

При сложной функции (2.18) и в особенности если это функция неВнскольких аргументов, отыскание закона распределения погрешности результата связано со значительными математическими трудностями. Поэтому при нелинейных косвенных измерениях приходится отказыВнваться от использования интервальных оценок погрешности результата, ограничиваясь приближенной верхней оценкой ее границ. В основе приВнближенного оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (2.18) и дальнейшая обработка результаВнтов, как при линейных измерениях.

Запишем выражение для полного дифференциала функции А:

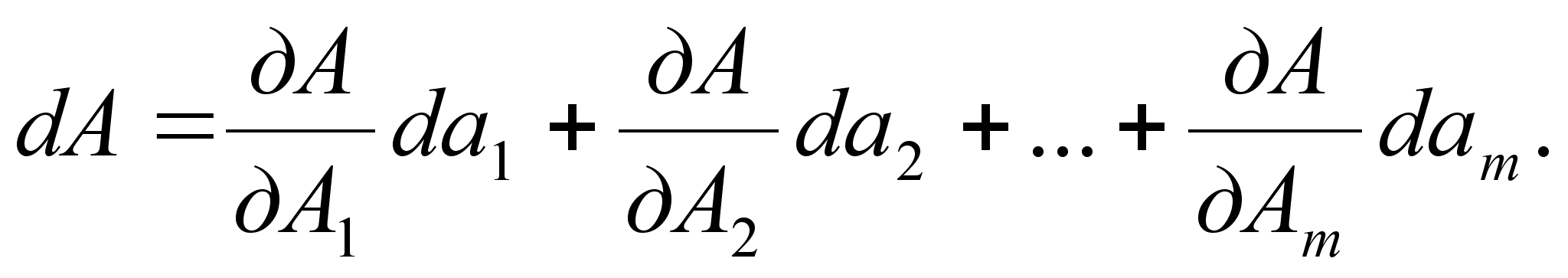
(2.23)

По определению полный дифференциал функции тАФ это приращение функции, вызванное малыми приращениями ее аргументов.

Учитывая, что погрешности измерения аргументов всегда являются малыми величинами по сравнению с номинальными значениями аргуВнментов, можно заменить в (2.23) дифференциалы аргументов dа_i, на поВнгрешности измерений а_i, а дифференциал функции dA на погрешность результата измерения :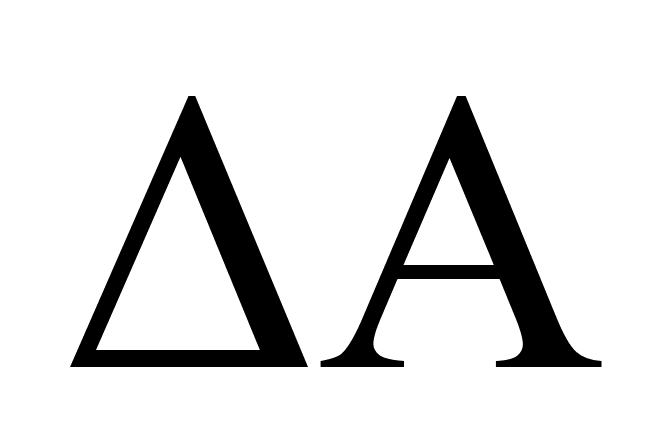

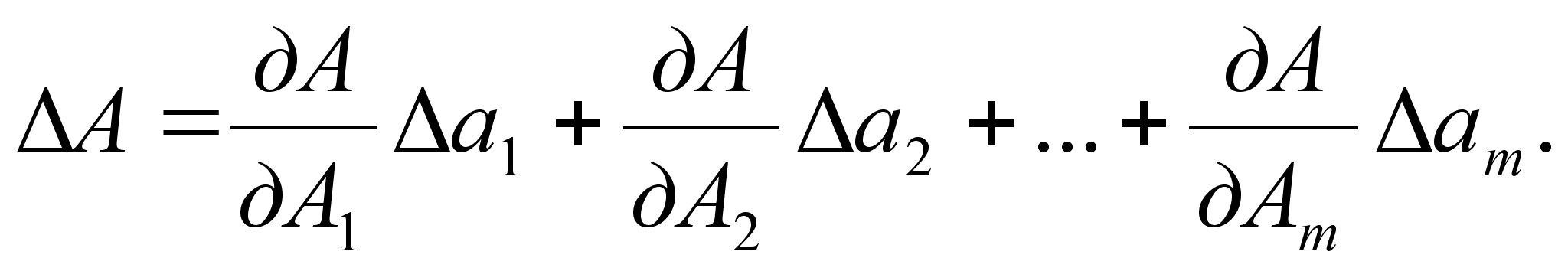
(2.24)

Полагая, как и прежде, что распределения погрешностей аргументов подчиняются равномерному закону, при числе слагаемых m < 5 граниВнцы погрешности результата можно определить по формуле (2.20). В том случае, когда погрешности аргументов заданы их доверительными граВнницами, оценку погрешности результата измерения вычисляют по (2.22). В обеих случаях роль коэффициентов b₁,b₂,тАж,b_m выполняют частные

производные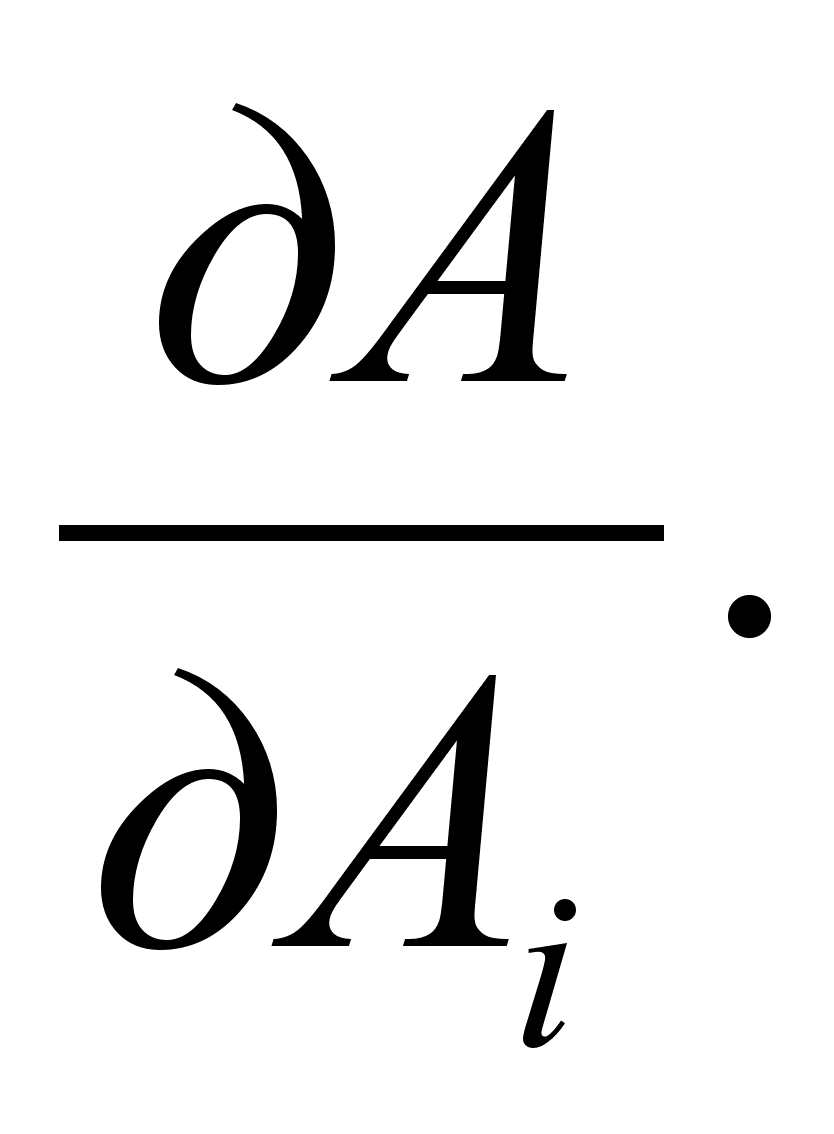

Применив формулу (2.24), получим несколько простых правил оцеВннивания погрешности результата косвенного измерения.

Правило 1. Погрешности в суммах и разностях. Если a₁ и а₂ измерены с погрешностями и и измеренные значения используВнются для вычисления суммы или разности А = а_1*а_2, то суммируются абсолютные погрешности (без учета знака):

Правило 2. Погрешности в произведениях и частных. Если изВнмеренные значения а₁, и а₂ используются для вычисления А = а_1* а₂ или А = а₁/а₂, то суммируются относительные погрешности 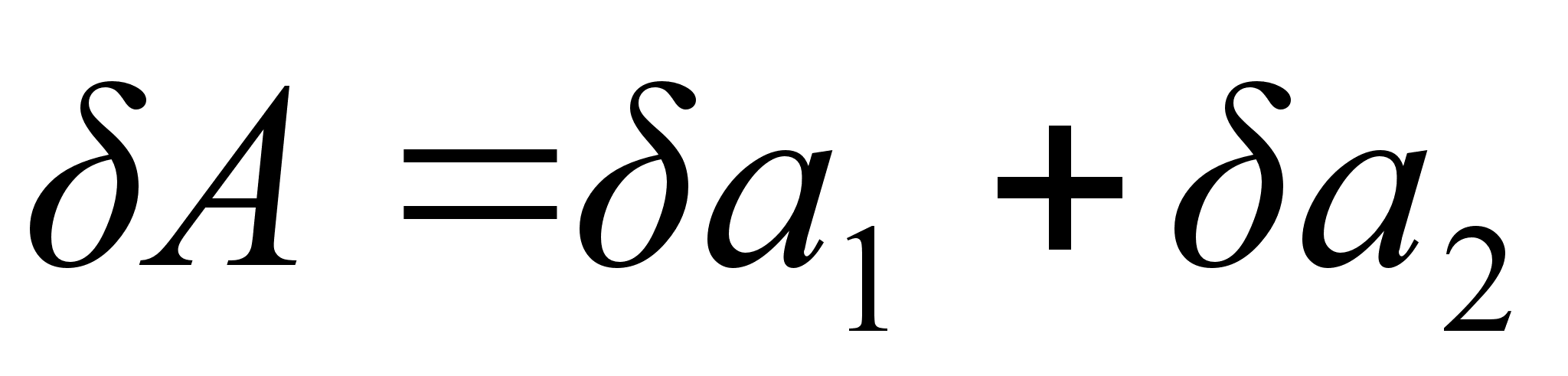, где .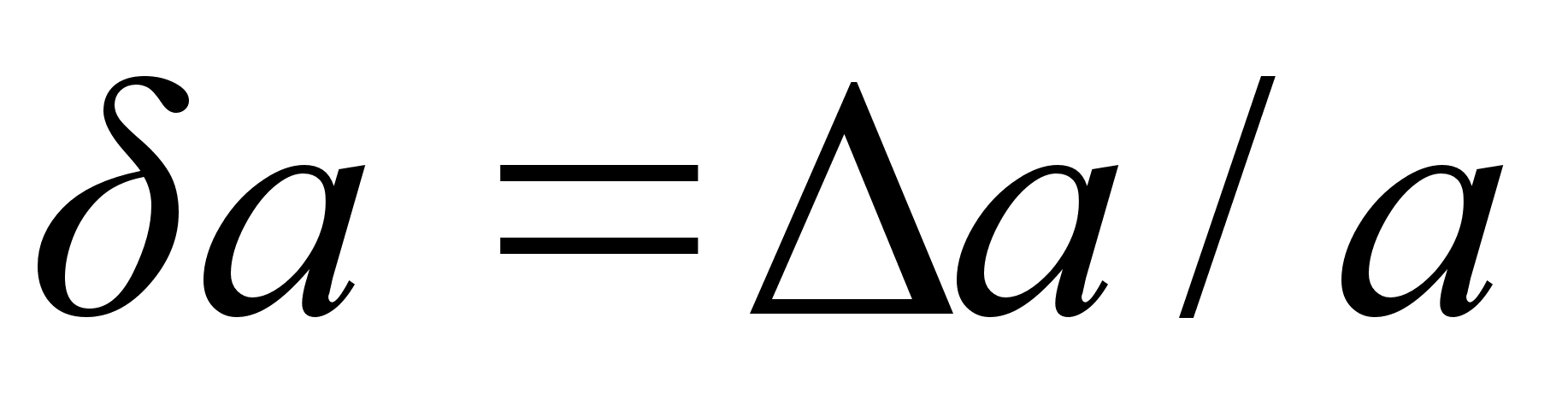

Правило 3. Измеренная величина умножается на точное число.

Если а используется для вычисления произведения А = В * а, в котором В не имеет погрешности, то А = |В|а .

Правило 4. Возведение в степень. Если а используется для вычисления степени А = аⁿ, то А = .

Правило 5. Погрешность в произвольной функции одной переВнменной. Если а используется для вычисления функции А(а), то

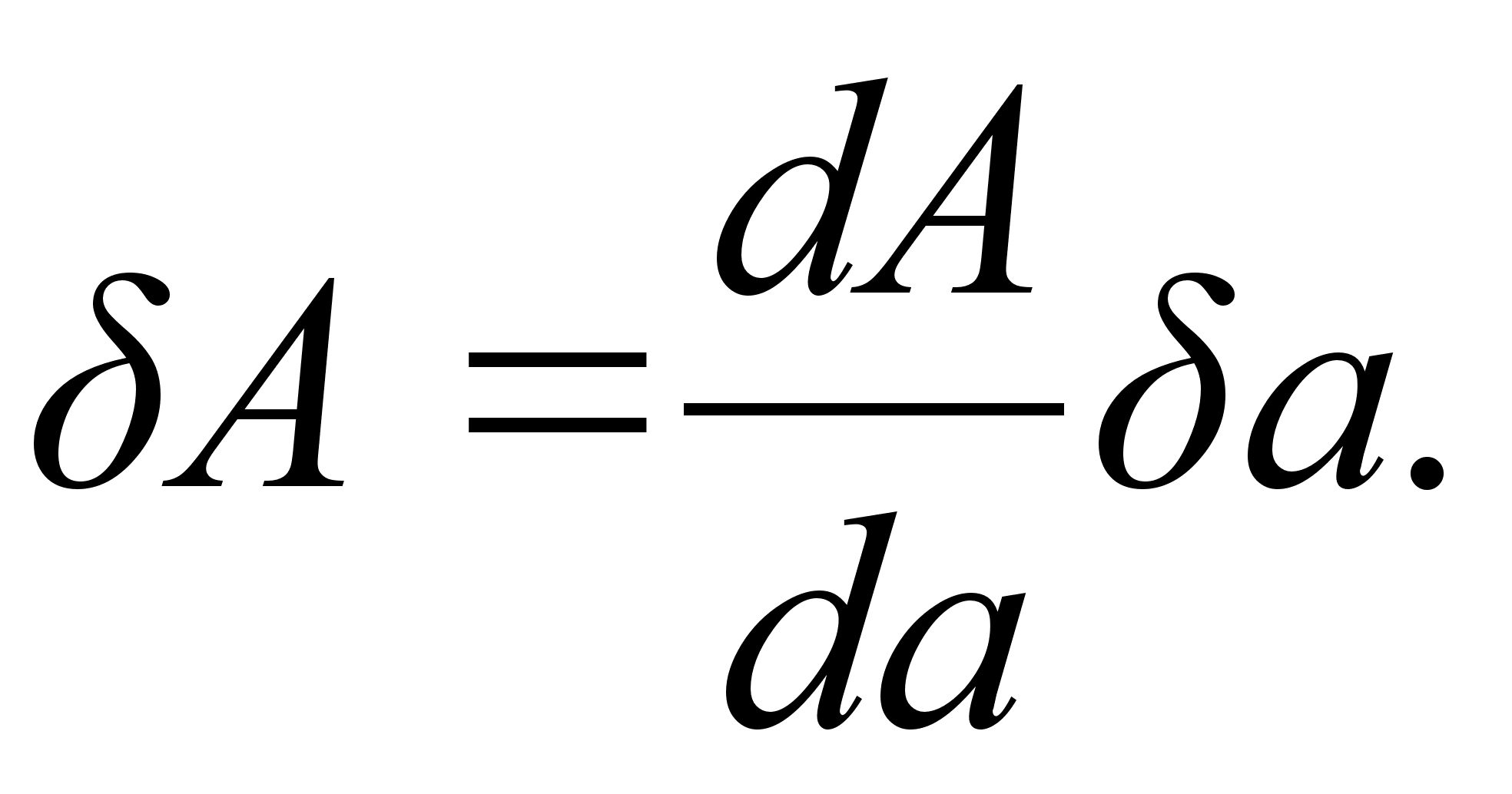
Вывод этих правил не приводится и может быть легко сделан самоВнстоятельно. Использование правил позволяет получить не слишком завыВншенную оценку предельной погрешности результата нелинейного косвенВнного измерения при не слишком большом числе аргументов (m < 5).

Пример. Производится косвенное измерение электрической мощности, рассеиваемой на резисторе сопротивлением R при протекании по нему тока I. Так как Р =I²R, то, приВнменяя правила 2 и 4, получим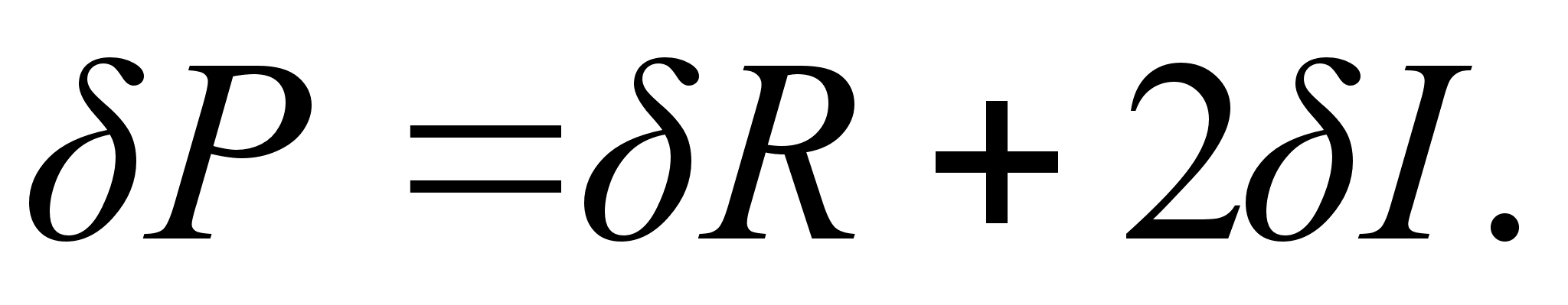

Пример. Измерением найдено значение утла 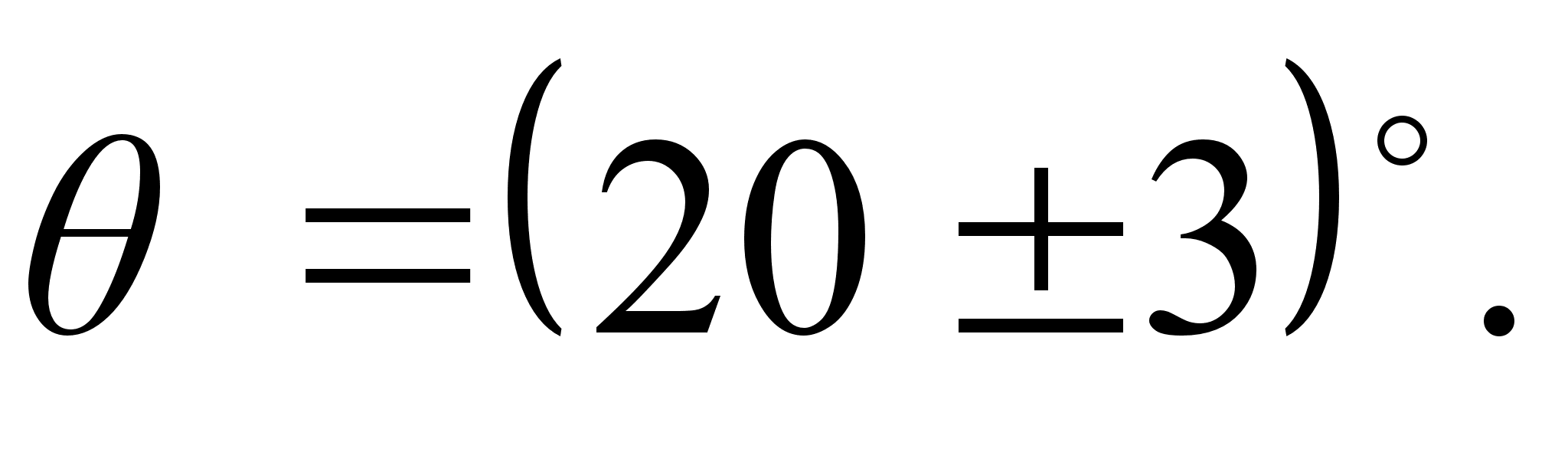Необходимо найти cos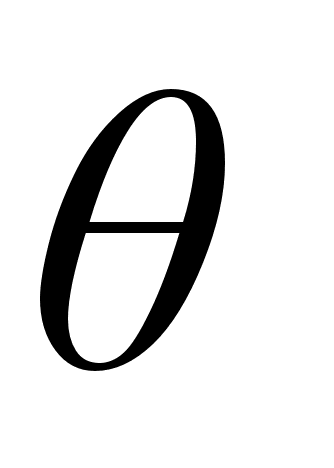. Наилучшая оценка для cos20В° = 0,94. Погрешность 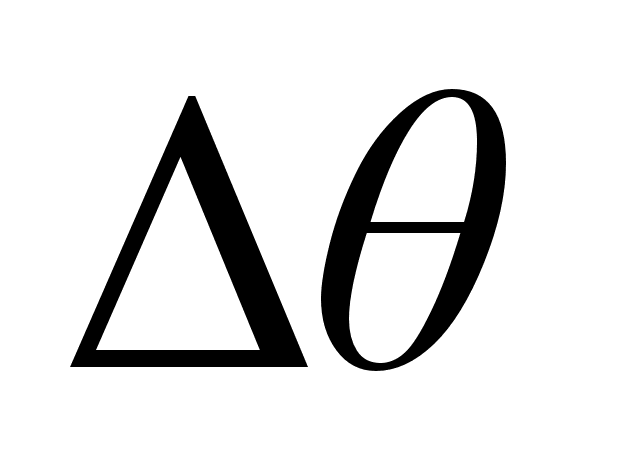должна быть выражена в радианах, т.е. 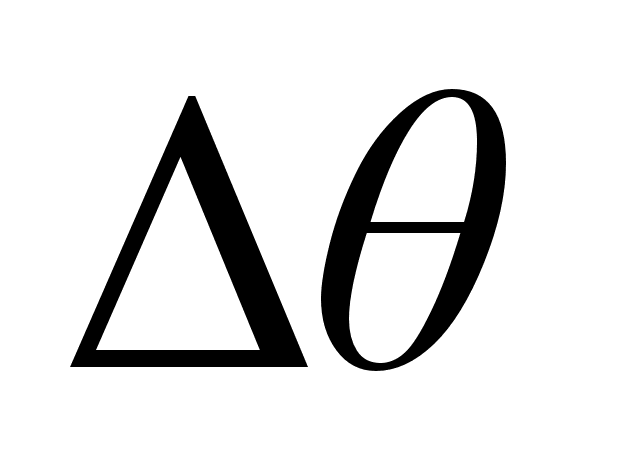= 3В° = 0,05 рад. Тогда по правилу 5 (cos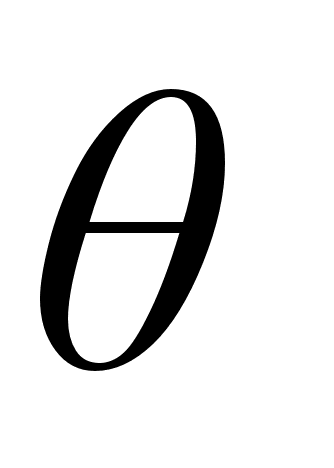) = (sin20В°)*0,05 = 0,34-0,05 = 0,02. Окончательно cos 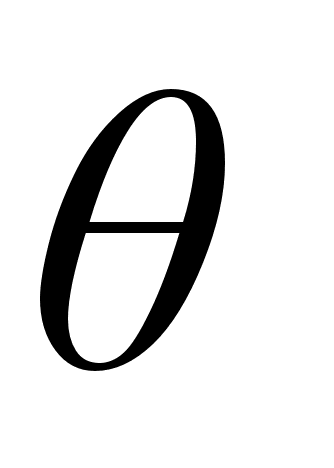= 0,94В±0,02 .

7.Преобразование измеряемой величины как косвенные измерения

При косвенных измерениях результат определяется на основании измерений величин, связанных с измеряемой величиной известной зависимостью. При этом в качестве примеров рассматривались случаи, когда закономерная зависимость выражалась строго математически. Однако строгая закономерность зависимости между величинами может быть неизвестна, хотя и известно, что такая зависимость существует. Например, известно, что электродвижущая сила термопары зависит от температуры. Определить эту зависимость на основании известных нам законов физики мы не можем даже для одной и той же пары металлов. На эту зависимостиь влияют малейшие отклонения в составах сплавов и технология их обработки. В этих случаях нужную нам зависимость мы можем определить методом совместных измерений. И не только определить, но и исследовать, и изучить постоянство и воспроизводимость этой зависимости влияния на нее внешних воздействий. Когда зависимость одной величины от другой будет нам хорошо известна, мы имеем возможность измерять нужную нам величину на основании измерений других величин, связанных с измеряемой известной зависимостью.

Описанные измерения следует также отнести к косвенным измерениям как одну из его разновидностей. Разновидностью косвенных измерений является также случай нахождения значения измеряемой величины путем прямых измерений компонентов известной формулы, определяющей ее зависимости от этих компонентов. Эта разновидность косвенных измерений относится к случаю нахождения значения измеряемой величины по ее зависимости от других величин, определяемой путем совместных измерений. Вторая разновидность косвенных измерений может рассматриваться так же, как измерение путем преобразования измеряемой величины в другую, по природе своей существенно отличающуюся от измеряемой, но связанную с ней устойчивой зависимостью.

Вместе с этим смотрят:

11-этажный жилой дом с мансардой

14-этажный 84-квартирный жилой дом

16-этажный жилой дом с монолитным каркасом в г. Краснодаре

180-квартирный жилой дом в г. Тихорецке

2-этажный 3-секционный 18-квартирный жилой дом в г. Мирном