Прикладная теория цифровых автоматов
1. ПОБУДОВА ОБ'РДДНАНОРЗ ГСА
1.1. Побудова ГСА
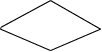
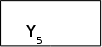
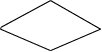
По описах граф-схем, приведених в завданнi до курсовоi роботи, побудуiмо ГСА Г1-Г5 (мал. 1.1-1.5), додавши початковi i кiнцевi вершини i замiнивши кожний оператор Yi операторною вершиною, а кожну умову Xi - умовною.
1.2. Методика об'iднання ГСА
У ГСА Г1-Г5 i однаковi дiлянки, тому побудова автоматiв за ГСА Г1-Г5 приведе до невиправданих апаратурних витрат. Для досягнення оптимального результату скористаiмося методикою С.РЖ.Баранова, яка дозволяi мiнiмiзувати число операторних i умовних вершин. Заздалегiдь помiтимо операторнi вершини в початкових ГСА, керуючись слiдуючими правилами:
1) однаковi вершини Yi в рiзних ГСА вiдмiчаiмо однаковими мiтками Aj;
2) однаковi вершини Yi в межах однiii ГСА вiдмiчаiмо рiзними мiтками Aj;
3) у всiх ГСА початкову вершину помiтимо як А0, а кiнцеву - як Ak.
На наступному етапi кожнiй ГСА поставимо у вiдповiднiсть набiр змiнних PnО {P1..Pq}, де q=]log2N[, N -кiлькiсть ГСА. Означувальною для ГСА Гn ми будемо називати кон`юнкцию Pn=p1eЩ..Щpqn еО{0,1}, причому p0=щр, p1=р. Об'iднана ГСА повинна задовольняти слiдуючим вимогам:
1) якщо МК Ai входить хоча б в одну часткову ГСА, то вона входить i в об'iднану ГСА Г0, причому тiльки один раз;
2) при пiдстановцi набору значень (е1..en), на якому Pq=1 ГСА Г0 перетворюiться в ГСА, рiвносильну частковiй ГСА Гq.
При об'iднаннi ГСА виконаiмо слiдуючi етапи:
-сформуiмо частковi МСА М1 - М5, що вiдповiднi ГСА Г1 - Г5;
- сформуiмо об'iднану МСА М0;
- сформуiмо системи дужкових формул переходу ГСА Г0;
- сформуiмо об'iднану ГСА Г0.
1.3. Об'iднання часткових ГСА
Частковi МСА М1-М5 побудуiмо по ГСА Г1-Г5 (мал.1.1) вiдповiдно. Рядки МСА вiдмiтимо всiма мiтками Ai, що входять до ГСА, крiм кiнцевоi Ak.




 ПОЧАТОК A0
ПОЧАТОК A0

 1
1


 0 X1 1
0 X1 1
2
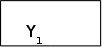
A1
 3
3
 0
0
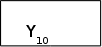
 4 X2 A2 1
4 X2 A2 1
 5
5
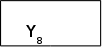
A3
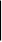
6
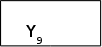
A4
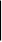
7
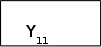
A5
 8
8
A6
9

A7
10

 A8
A8




 КiНЕЦь Ak
КiНЕЦь Ak

Мал.1.1. Часткова граф-схема алгоритму Г1




 ПОЧАТОК A0
ПОЧАТОК A0

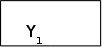 1
1



 A1
A1
2

A7
 0 3 1
0 3 1

 X3
X3
4 5
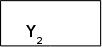
 A9 A6
A9 A6
6 7
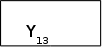
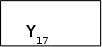
A10 A12
8 9

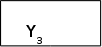
A3 A22
10
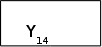
A11




 КiНЕЦЬ Ak
КiНЕЦЬ Ak

Мал.1.2. Часткова граф-схема алгоритму Г2




 ПОЧАТОК A0
ПОЧАТОК A0

1
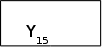
A11
 0 2 1
0 2 1

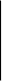

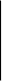

 X1
X1
 3 4
3 4
 A15 A16
A15 A16

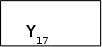 6
6
5 1
 X3 A12
X3 A12
 0
0
7 8
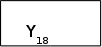

 A6 A13
A6 A13

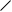
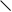
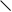
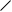




 КiНЕЦЬ Аk
КiНЕЦЬ Аk

Мал.1.3. Часткова граф-схема алгоритму Г3




 ПОЧАТОК A0
ПОЧАТОК A0

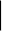

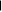 1
1
0 1

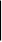

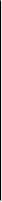

 X1
X1
2
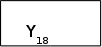
A13
3
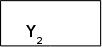
A9
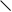

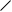 4
4

A8
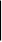
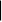
 5
5
1 X2


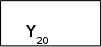
 6 0
6 0
A17
7

A6
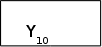 8
8
A2
9

A18





 КiНЕЦЬ Ak
КiНЕЦЬ Ak

Мал.1.4. Часткова граф-схема алгоритму Г4






 ПОЧАТОК A0
ПОЧАТОК A0
1
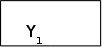
A1
2

A6
3
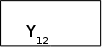
A19
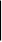
 4
4
0 1

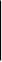

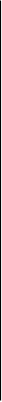 X1
X1
 5
5
0 X2

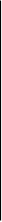
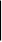 1
1
6
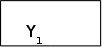
A20
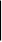
7

A17
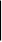

 8
8
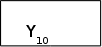
A2

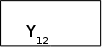 9
9
A21




 КiНЕЦЬ Ak
КiНЕЦЬ Ak

Мал.1.5. Часткова граф-схема алгортиму Г5
Стовпцi МСА вiдмiтимо всiма мiтками AiВн, що входять до ГСА, крiм початковоi A0. На перетинi рядка Ai i стовпця Aj запишемо формулу переходу fij вiд оператора Ai до оператора Aj. Ця функцiя дорiвнюi 1 для безумовного переходу або кон`юнкцii логiчних умов, вiдповiдних виходам умовних вершин, через якi проходить шлях з вершини з мiткою Ai у вершину з мiткою Aj.
За методикою об'iднання закодуiмо МСА таким чином:
Таблиця 1.1
Кодування МСА
МСА | P1P2P3 |
М1 | 0 0 0 (щp1щp2щp3) |
М2 | 0 0 1 (щp1щp2p3) |
М3 | 0 1 0 (щp1p2щp3) |
М4 | 0 1 1 (щp1p2p3) |
М5 | 1 0 0 (p1щp2щp3) |
Частковi МСА М1-М5 наведенi в табл.1.2-1.6
Таблиця 1.2
Часткова МСА М1
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | Ak |
A0 | щx1 | щx1щx2 | x1x2 |
|
|
|
|
|
|
A1 |
| 1 |
|
|
|
|
|
|
|
A2 |
|
|
|
|
| 1 |
|
|
|
A3 |
|
|
| 1 |
|
|
|
|
|
A4 |
|
|
|
| 1 |
|
|
|
|
A5 |
|
|
|
|
| 1 |
|
|
|
A6 |
|
|
|
|
|
| 1 |
|
|
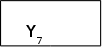
A7 |
|
|
|
|
|
|
| 1 |
|
A8 |
|
|
|
|
|
|
|
| 1 |
Таблиця 1.3
Часткова МСА М2
| A1 | A3 | A6 | A7 | A9 | A10 | A11 | A12 | A22 | Ak |
A0 | 1 |
|
|
|
|
|
|
|
|
|
A1 |
|
|
| 1 |
|
|
|
|
|
|
A3 |
|
|
|
|
|
| 1 |
|
|
|
A6 |
|
|
|
|
|
|
| 1 |
|
|
A7 |
|
| x3 |
| щx3 |
|
|
|
|
|
A9 |
|
|
|
|
| 1 |
|
|
|
|
A10 |
| 1 |
|
|
|
|
|
|
|
|
A11 |
|
|
|
|
|
|
|
|
| 1 |
A12 |
|
|
|
|
|
|
|
| 1 |
|
A22 |
|
|
|
|
|
|
|
|
| 1 |
Таблиця 1.4
Часткова МСА М3
| A6 | A12 | A13 | A14 | A15 | A16 | Ak |
A0 |
|
|
| 1 |
|
|
|
A6 |
|
|
|
|
|
| 1 |
A12 |
|
| 1 |
|
|
|
|
A13 |
|
|
|
|
|
| 1 |
A14 |
|
|
|
| щx1 | x1 |
|
A15 | x3 |
|
|
|
|
| щx3 |
A16 |
| 1 |
|
|
|
|
|
Таблиця 1.5
Часткова МСА М4
| A2 | A6 | A8 | A9 | A13 | A17 | A18 | Ak |
A0 |
|
| щx1 |
| x1 |
|
|
|
A2 |
|
|
|
|
|
| 1 |
|
A6 | 1 |
|
|
|
|
|
|
|
A8 |
|
|
|
|
| x2 |
| щx2 |
A9 |
|
| 1 |
|
|
|
|
|
A13 |
|
|
| 1 |
|
|
|
|
A17 |
| 1 |
|
|
|
|
|
|
A18 |
|
|
|
|
|
|
| 1 |
Таблиця 1.6
Часткова МСА М5
| A1 | A2 | A6 | A17 | A19 | A20 | A21 | Ak |
A0 | 1 |
|
|
|
|
|
|
|
A1 |
|
| 1 |
|
|
|
|
|
A2 |
|
|
|
|
|
| 1 |
|
A6 |
|
|
|
| 1 |
|
|
|
A17 |
| 1 |
|
|
|
|
|
|
A19 |
| x1щx2 |
|
|
| x1x2 | щx1 |
|
A20 |
|
|
| 1 |
|
|
|
|
A21 |
|
|
|
|
|
|
| 1 |
На наступному етапi побудуiмо об'iднану МСА М0, в якiй рядки вiдмiченi всiма мiтками Аi, крiм Аk, а стовпцi - всiма, крiм А0. На перетинi рядка Аi i стовпця Аj запишемо формулу переходу, яка формуiться таким чином: Fij=P1fij1+..+Pnfijn (n=1..N). Де fijn-формула переходу з вершини Аi у вершину Аj для n-оi ГСА. Наприклад, формула переходу А0ВоА1 буде мати вигляд F0,1=щx1щp1щp2щp3+ щp1щp2p3+ +p1щp2щp3. У результатi ми отримаiмо об'iднану МСА М0 (табл.1.7). Ми маiмо можливiсть мiнiмiзувати формули переходу таким чином: розглядаючи ГСА Г0 як ГСА Гn, ми пiдставляiмо певний набiр Pn=1, при цьому змiннi p1.pq не змiнюють своiх значень пiд час проходу по ГСА. Таким чином, якщо у вершину Аi перехiд завжди здiйснюiться при незмiнному значеннi pq, то це значення pq в рядку Аi замiнимо на “1", а його iнверсiю на “0". Наприклад, у вершину А3 перехiд здiйснюiться при незмiнному значеннi щp1 i щp2, отже в рядку А3щp1 i щp2 замiнимо на “1", а p1 i p2 на “0". У результатi отримаiмо формули F3,4=щp3, F3,11=p3. Керуючись вищенаведеним методом, отримаiмо мiнiмiзовану МСА М0 (табл.1.8).
По таблицi складемо формули переходу для об'iднаноi ГСА Г0. Формулою переходу будемо називати слiдуюче вираження: AiВоFi,1А1+.+Fi,kАk, де Fi,j-вiдповiдна формула переходу з мiнiмiзованоi МСА. У нашому випадку отримаiмо слiдуючу систему формул:
A0Вощx1щp1щp2щp3A1+щp1щp2p3A1+p1щp2щp3A1+x1щx2щp1щp2щp3A2+x1x2щp1щp2щp3A3+
+щx1щp1p2p3ВнA8+x1щp1p2p3A13+щp1p2щp3A14
A1Вощp1щp3A2Вн+p1щp3A6+щp1p3A7
A2Вощp1щp2щp3A6+щp1p2p3A18+p1щp2p3A21
A3Вощp3A4+p3A11
A4ВоA5
A5ВоА6
Таблиця 1.7
Об`iднана МСА Мo
|
A1
|
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
A18 |
A19 |
A20 |
A21 |
A22 |
Ak |
A0 | _ _ _ _ x1p1p2p3+ _ _ +p1p2p3+ _ _ +p1p2p3
| _ _ _ _ x1x2p1p2p3 | _ _ _ x1x2p1p2p3 |
|
|
|
| _ _ x1p1p2p3 |
|
|
|
| _ x1p1p2p3 | _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
A1 |
| _ _ _ p1p2p3 |
|
|
| _ _ p1p2p3 | _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
| _ _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
| _ p1p2p3 |
|
| _ _ p1p2p3 |
|
|
A3 |
|
|
| _ _ _ p1p2p3 |
|
|
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
| _ _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A5 |
|
|
|
|
| _ _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A6 |
| _ p1p2p3 |
|
|
|
| _ _ _ p1p2p3 |
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
| _ _ p1p2p3 |
|
|
| _ _ p1p2p3 |
A7 |
|
|
|
|
| _ _ x3p1p2p3 |
| _ _ _ p1p2p3 | _ _ _ x3p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ x2p1p2p3 |
|
|
|
|
| _ _ _ p1p2p3+ _ _ +x2p1p2p3 |
A9 |
|
|
|
|
|
|
| _ p1p2p3 |
| _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A10 |
|
| _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
A12 |
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
|
|
| _ _ p1p2p3 |
|
A13 |
|
|
|
|
|
|
|
| _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
A14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
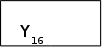
| _ _ _ x1p1p2p3 | _ _ x1p1p2p3 |
|
|
|
|
|
|
|
A15 |
|
|
|
|
| _ _ x3p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ _ x3p1p2p3 |
A16 |
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
A17 |
| _ _ p1p2p3 |
|
|
| _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ p1p2p3 |
A19 |
| _ _ _ x1x2p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ x1x2p1p2p3 | _ _ _ x1p1p2p3 |
|
|
A20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
|
A21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
A22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ _ p1p2p3 |
Таблиця 1.8
Об`iднана мiнiмiзована МСА Мo
|
A1
|
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
A18 |
A19 |
A20 |
A21 |
A22 |
Ak |
A0 | _ _ _ _ x1p1p2p3+ _ _ +p1p2p3+ _ _ +p1p2p3
| _ _ _ _ x1x2p1p2p3 | _ _ _ x1x2p1p2p3 |
|
|
|
| _ _ x1p1p2p3 |
|
|
|
| _ x1p1p2p3 | _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
A1 |
| _ _ p1p3 |
|
|
| _ p1p3 | _ p1p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
| _ _ _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
| _ p1p2p3 |
|
| _ _ p1p2p3 |
|
|
A3 |
|
|
| _ p3 |
|
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A6 |
| _ p1p2p3 |
|
|
|
| _ _ _ p1p2p3 |
|
|
|
| _ _ p1p2p3 |
|
|
|
|
|
| _ _ p1p2p3 |
|
|
| _ _ p1p2p3 |
A7 |
|
|
|
|
|
x3p3 |
| _ p3 | _ x3p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2p2p3 |
|
|
|
|
| _ _ p2p3+ _ +x2p2p3 |
A9 |
|
|
|
|
|
|
|
p2 |
| _ p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A10 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A12 |
|
|
|
|
|
|
|
|
|
|
|
| _ p2p3 |
|
|
|
|
|
|
|
| _ p2p3 |
|
A13 |
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
|
|
|
|
| _ p3 |
A14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ x1 |
x1 |
|
|
|
|
|
|
|
A15 |
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| _ x3 |
A16 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
A17 |
| _ _ p1p2p3 |
|
|
| _ p1p2p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A19 |
| _ x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 | _ x1 |
|
|
A20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
A21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A6Вощp1p2p3A2+щp1щp2щp3A7+щp1щ
Вместе с этим смотрят:
11-этажный жилой дом с мансардой
14-этажный 84-квартирный жилой дом
16-этажный жилой дом с монолитным каркасом в г. Краснодаре
180-квартирный жилой дом в г. Тихорецке
2-этажный 3-секционный 18-квартирный жилой дом в г. Мирном