Система автовождения карьерного автосамосвала
Введение
В последние годы за рубежом ведутся интенсивные работы по созданию и внедрению систем автоматического управления горным автотранспортом. Так, на ряде карьеров Канады и США внедрены системы диспетчерского управления работой автотранспорта с использованием компьютерной техники, а также системы автоматического вождения (САВ) автосамосвалов по трассам между точками загрузки и разгрузки. Отмечается, что автоматизированное управление работой автотранспорта позволяет повысить его производительность более, чем на 20%.
Эффективность системы автовождения проверена в карьере, где работают 10 экскаваторов и 54 самосвала. САВ уменьшает в два раза время ручного управления, увеличивает на 6,9% время использования экскаваторов и на 25% коэффициент использования автосамосвалов.
Однако существующие САВ не обеспечивают автоматического или полуавтоматического маневрирования машин в местах погрузки и разгрузки, где применяемая система с излучающим проводом, проложенным вдоль трассы, становится бесполезной из-за случайного характера траекторий маневрирования и наличия непредвиденных препятствий. Между тем, маневры у бровки отвала в условиях плохого заднего обзора и наличия препятствий отнимают значительное время и связаны с повышенным риском для машины и водителя. По статистическим данным аварии и катастрофы на разгрузке составляют до 10% от общего числа аварий на горном транспорте.
Таким образом, система автовождения карьерного автосамосвала должна обеспечивать не только движение по трассе между пунктами загрузки и разгрузки, но и маневрирование в местах разгрузки (если будет решена эта проблема, то управление в местах загрузки не будет представлять трудностей). В этом случае задача осуществления маневра является одной из основных для САВ карьерного автосамосвала.
1. Планирование траектории.
1.1 Обоснование необходимости автоматического
планирования и отслеживания траектории.
Наиболее важным направлением автоматизации работы карьерного транспорта является автоматизация движения самосвалов в местах разгрузки. В связи с тем, что в контуре управления присутствует человек, отсутствует гарантия в следующих аспектах:
выбор оптимальной траектории;
точность остановки в точке разгрузки (ошибка может привести к аварии);
несогласованность манёвров самосвалов в зоне разгрузки;
Для устранения указанных проблем требуется автоматизировать построение траектории. Автоматизация построения траектории и следования по ней усложняется следующими факторами:
сложность и не постоянство площадки;
случайный характер траекторий;
необходимость учитывать динамические и геометрические особенности самосвала;
отсутствие на местности характерных точек и ориентиров;
невозможность предварительного указания траектории на местности из - за тяжёлых условий работы известных средств, указывающих траектории (большие массы самосвалов, работа бульдозера, плохие погодные условия и др.).
Для удачной работы САВ необходимо кроме создания оптимальной траектории ещё и отслеживать правильность движения по ней, а также оперативно вносить в неё изменения по мере накопления данных о местности и изменения расположения препятствий. В связи с этим в разрабатываемой САВ введены подсистемы ориентации и программное определение координат и ориентации самосвала по счислению. Использование двух независимых источников информации об ориентации самосвала позволяет повысить надёжность САВ и оперативность предоставления данных программам и системам, которые в таких данных нуждаются. Автоматическое отслеживание прохождения по запланированной траектории позволит вовремя переключить режимы планирования траектории и прохождения по ней.
1.2 Требования к траектории и
к алгоритму выбора траектории.
Сформированная программно траектория должна удовлетворять следующим требованиям:
Должна учитывать геометрические и технологические особенности транспортного средства для которого планируется траектория. При расчёте поворота должен быть учтён технологический радиус (минимальный радиус поворота транспортного средства), скорость транспортного средства (ТС), коэффициент сцепления и другие внешние и внутренние факторы, влияющие на динамику ТС.
Должна проходить на расстоянии от препятствий, достаточном для нормального безопасного проезда.
Должна быть как можно короче и содержать минимум поворотов.
Повороты должны быть такими, что бы самосвал на них не заносило, значит по мере изменения скорости её вид может меняться.
При движении задним ходом она должна легко задаваться , точно и легко отслеживаться.
В соответствии с указанными требованиями алгоритм должен удовлетворять следующим требованиям:
максимальное быстродействие;
небольшая потребность в процессорном времени;
должен уметь воспроизводить прямые простейшие кривые по которым может двигаться самосвал;
должен учитывать особенности планирования движения задним ходом.
В связи с этим применимы алгоритмы планирования траектории по карте местности.
1.3 Геометрические особенности реализации алгоритмов.
Для демонстрации указанных особенностей, нанесём на миллиметровую бумагу горизонтальную проекцию самосвала. Для наиболее удобной аппроксимации реальной проекции автомобиля выберем отношение длины проекции к её ширине равным 9:5. (рис. 2.1) Для выявления критерия возможности проезда под углом 450 расположим проекцию автосамосвала под углом 450 и пометим занятые ею квадраты со стороной в одну дискрету. Повёрнутый таким образом самосвал занимает площадь 11 х 11 дискрет. При любой другой ориентации самосвал займёт прямоугольник заведомо меньшей площади и максимальной длины, следовательно если центр самосвала можно расположить в квадрате 11 х 11 дискрет так, чтобы в нём не было препятствий, значит траектория может проходить через данную точку. В целях повышения быстродействия желательно произвести поиск и указание таких точек до начала поиска траектории чтобы избежать повторных поисков препятствий в квадрате.
Для определённости на карте будут определяться лишь геометрические места центров автомобиля.
При рассмотрении критериев разрешения поворота, нанесём на карту положение самосвала до и после поворота, и проведем окружности таким образом, чтобы охватить все промежуточные положения крайних точек автосамосвала. Соединив начальную и конечную точки поворота последовательностью клеток - дискрет на карте наиболее близких к полученной дуге можно увидеть, что длина прямого участка на карте, параллельного осям должна быть не менее одной дискреты, а дина наклонного участка - не менее трёх.
Следовательно стоит предписать алгоритмам, чтобы точка излома траектории находилась не в реальном начале поворота, а была смещена назад на указанное выше количество дискрет в зависимости от направления. Следует также запретить излом траектории в случае диагонального движения менее чем в семи дискретах от предыдущего излома и трёх дискретах при движении вдоль осей.
1.4 Сравнительная характеристика
приведённых алгоритмов.
Для сравнения рассмотрим два имеющихся алгоритма планирования траектории: метод пробных траекторий и однослойная нейронная сеть. Метод пробных траекторий заключается в переборе вариантов траекторий, представляющих собой ломанные линии, соединяющие начальную и конечную точки по определённым правилам. Этот алгоритм применим только на достаточно простых площадках, допускающих небольшое количество вариантов траекторий. Преимуществом является то, что траектория планируется сразу от начала до конца, недостатки - 1) при необходимости внесения изменений в траекторию требуется её заново планировать, 2) невозможно спланировать разворот и подъезд задним ходом.
Алгоритм планирования по однослойной нейронной сети заключается в формировании оценки для каждого возможного (учитывая дискретность) направления. В формировании оценки участвуют следующие показатели: расстояние до ближайшего препятствия, текущая ориентация транспортного средства, скачёк расстояний до препятствия, направление на цель движения. По данному алгоритму принимается решение лишь о небольшом ближайшем участке движения, траектория не выстраивается как единое целое, из - за чего может быть не оптимальной. Данный алгоритм также не позволяет планирование разворота и учёт движения препятствий.
В связи с этим был разработан алгоритм планирования траектории, позволяющий быстро соединить две точки поверхности кратчайшей линией, проведённой с учётом легко вводимых и легко реализуемых критериев оптимальности. Кроме того разработанный алгоритм позволяет легко учесть геометрические особенности транспортного средства и легко к ним адаптируется.
Сравнительная характеристика приведённых и предлагаемого алгоритмов приведена в таблице 1.1
Таблица 1.1 Сравнение алгоритмов планирования траектории.
Критерий | Наименование алгоритма |
| Нейронная сеть | Пробных траекторий | Предлагаемый алгоритм |
1 | 2 | 3 | 4 |
Требования к памяти | 6*n2 чисел с плавающей запятой
|
18*Xmax *Ymax байт |
| Реализуемость на языке низкого уровня |
Неудобно |
Удобно |
| Качество полученной траектории | Не гарантируется | Гарантируется |
| Время работы | Зависит от 6*n2 | Неопределённо | Небольшое, чем ближе к концу - тем быстрее |
| Полнота использования информации | Использует только видимый в данный момент участок поля |
Полученная информация используется полностью |
| Сложность адаптации | Не требуется | Для адаптации требуется замена карты в памяти ЭВМ. |
| Влияние формы зоны осмотра | Нормально применим только при обзоре на 3600 | Не влияет |
| От чего зависит дискрета | От количества направлений n | От требуемых точности, быстродействия, качества траектории |
| Учёт участка движения задним ходом |
Невозможен |
Легко выполняется. |
| Дальнейшая оптимизация | Не требуется | Требуется ВлсрезаниеВ» углов |
2 Описание предлагаемого алгоритма
автоматического построения траектории
и навигации по счислению.
2.1 Предварительное планирование траектории.
В разработанном алгоритме строится карта местности в дискретах 1,25х1,25 м (связано с адекватным отображением самосвала на карте), считается, что самосвал занимает на карте площадь 5х9 дискрет. Траектория, получаемая по алгоритму является траекторией центра самосвала. Возможность перемещения центра самосвала на новую позицию определяется возможностью позиционирования центра самосвала в данной точке, при этом учитывается любая возможная ориентация самосвала.
Для ускорения планирования предполагается, что самосвал может поворачивать на угол 450 . т. е. Мы получаем восемь возможных направлений перемещения самосвала. Траектория строится по следующим критериям: минимальная длина, минимальное количество повротов.
Алгоритм заключается в следующем:
1) составляется массив 8 х a x b, где a и b - стороны прямоугольника, в который вписывается карта.
2) перед началом поиска этот массив заполняется нулями;
3) определяется точка конца траектории;
4) счётчик расстояния и искатель устанавливается на ноль;
из найденной точки делается шаг в любом возможном направлении;
если шаг параллельно осям координат - к счётчику расстояния прибавляется 10, иначе - 14;
7) значение счётчика записывается в ячейку N x X x Y, где N - направление; X, Y - координаты текущей позиции;
искатель увеличивается на 1;
происходит поиск ячеек со значением равным искателю;
если такая ячейка найдена, то от неё делаются ходы во всех возможных направлениях, при этом счётчики расстояний соответствующим образом модифицируются и записываются в новые ячейки;
если искатель достиг входа увеличиваем счётчик достижений на 1, иначе переход к пункту 8;
если счётчик достижений равен менее двух переходим к пункту 8;
обратный поиск маршрута: в точке входа находим направление, оценка расстояния которого минимальна;
делаем ход навстречу этому направлению;
если достигли входа - конец;
отыскиваем направление, оценка расстояния в котором минимальна;
переход к пункту 14.
Реальный поворот самосвала на карте и в виде траектории моделируется участком ломанной (приложение 2), содержащим излом на В±450 (в зависимости от направления) предполагается, что поворот начинается (заканчивается) раньше (позже) точки излома для ортогонального перемещения на одну дискрету, а для наклонного к осям координат на три. Вид поворота на карте приведён на рис. 2.1. В связи с этим длина прямого горизонтального участка допускается не менее трёх шагов, а наклонного - не менее семи шагов.
Приблизительный вид массива в конце траектории по окончании работы алгоритма будет иметь вид, показанный на рисунке 2.2 (траектория проходит через закрашенные клетки закрашенные клетки). В результате работы алгоритма будет получена траектория, представляющая собой незамкнутую ломанную, соседние звенья которой наклонены друг относительно друга на угол В±450 . Время работы этого алгоритма на процессоре PENTIUM S - 75 приблизительно 0,2 с., если учесть, что для проезда от начала до конца требуется запускать алгоритм лишь однажды, то быстродействие его можно считать достаточным.

Описанный алгоритм применим не только к самосвалу, но и после геометрической адаптации к любому транспортному средству, в частности он позволит двигаться транспортному роботу в недетерминированной (не разбитой на кварталы) среде.
В связи с тем, что поиск конкретного числа в трёхмерном массиве, содержащем десятки тысяч чисел слишком долог, был применён стековый метод накопления координат и направлений. Он заключается в следующем. В области данных программы выделено шестнадцать одинаковых областей для хранения данных. Эти области поочерёдно заполняются данными о координатах, направлении и длине последнего ровного участка. При обработке одна из шестнадцати областей служит источником данных, а остальные накапливают информацию о новых достигнутых клетках. По окончании обработки одной области программа приступает к извлечению данных из следующей, а область, обработанная только что используется для накопления следующей порции данных. Для упрощения обслуживания областей используется массив дескрипторов, в котором хранится информация об адресе области и о глубине её заполнения, а также введён специальный флаг, который устанавливается при исчерпании текущей области стека.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 61 |
|
| 71 |
|
| 81 |
11 | 19/1 |
|
| 1A/1 |
|
| 1B/1 | 11 |
| 1C/1 | 21 |
| 1D/1 | 31 |
| 1E/1 | 41 |
| 1F/1 | 51 |
| 20/1 | 61 |
| 21/1 | 71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 19/2 |
|
| 1A/2 |
|
| 1B/2 |
|
| 1C/2 | 26 |
| 1D/2 | 36 |
| 1E/2 | 46 |
| 1F/2 | 56 |
| 20/2 | 66 |
| 21/2 | 76 |
15 |
|
|
| 11 |
|
|
| 15 |
|
| 26 |
|
| 36 |
|
| 46 |
|
| 56 |
|
| 66 |
|
| 76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1F/3 |
|
| 20/3 |
|
| 21/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 61 |
|
| 71 |
|
| 81 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 20/4 |
|
| 21/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 75 |
|
| 85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 21/5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 89 |
Рис 2.2. Приблизительный вид массива в конце траектории по окончании работы алгоритма.
Программная реализация этого алгоритма выполнена на Ассемблере. Этот язык программирования выбран по тому, что программы разработанные на нём обладают наибольшим быстродействием и занимают минимальный объем памяти. Языки высокого уровня не смогут обеспечить требуемое быстродействие (размер программы не критичен) и содержат внутренние ошибки не поддающиеся устранению.
2.2 Сглаживание поворотов.
По окончании первичного планирования траектории (п 2.1) мы будем иметь предварительную траекторию, представляющую собой ломанную, каждое из звеньев которой повёрнуто на угол с450 относительно предыдущего звена. Данная траектория имеет низкое качество по сравнению с достижимой, поэтому требуется произвести сглаживание (Влсрезание угловВ»). Именно это и будет выполнятся при вторичном планировании.
В целях экономии времени, алгоритм сглаживания будет запускаться для ближайшего поворота (как исключение и для следующего). При сглаживании программа будет пытаться провести траекторию между любыми двумя точками до начала ближайшего поворота и после его окончания. Для повышения быстродействия программа начнёт с минимального сглаживания (малое удачное сглаживание более вероятно), а затем попытается удлинить отрезок сглаживания. Попытки Влсрезать уголВ» будут прекращены как только исчезнет возможность осуществить сглаживание. Отрезок сглаживания будет проводится через клетки на которых возможно нахождение центра самосвала и ориентация самосвала в любом направлении.
В результате удачного сглаживания (рис.2.3 - 2.5), вместо поворотов на с450 возникнут два поворота на угол менее 450 и отрезок сглаживания, длина которого будет меньше суммарной длины всех частей ломанной, расположенных между концами отрезка сглаживания. В связи с тем, что в программу, выполняющую первую стадию планирования не заложены повороты на эти углы (j1 и j2), алгоритм сглаживания по формулам должен будет определить точку начала поворота (r1 и r2). Указанные на рис. 3.3 величины найдём по формулам 2.1 - 2.5.
 (2.1);
(2.1);

j1=arccos
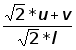
(2.2);
j2=arccos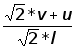 (2.3);
(2.3);
r1=R*tg(j1/2) (2.4);
r2=R*tg(j2/2) (2.5).
В случае поворота, изображенного на рисунке 2.4, величины, его определяющие, рассчитаем по формуле 2.6 и 2.7:
j=arctg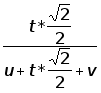 (2.6)
(2.6)
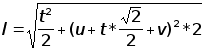 (2.7).
(2.7).
Как в первом, так и во втором случаях линия lпроводится таким образом, чтобы она не проходила через клетки, на которые запрещён въезд самосвала. В случае для рисунка 2.6 по формулам 2.8 и 2.9: 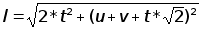 (2.8);
(2.8);
j=arctg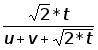 (2.9).
(2.9).
Возможна ситуация, когда конец сглаживания поворота совпадает с началом сглаживания следующего поворота (рис 2.6). В этом случае угол (j5) между отрезками сглаживания l1 и l2 вычисляется по формуле 2.7, а упреждение поворота по формуле 2.4 (2.5), но с j5 вместо j2 ,
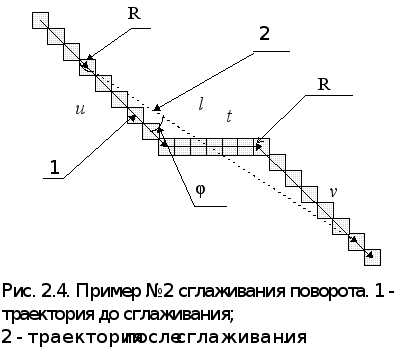
В случае, если сглаживание данного поворота произвести не удалось, то начинать поворот требуется на одну дискрету раньше точки излома на карте (при до поворота движении параллельно осям

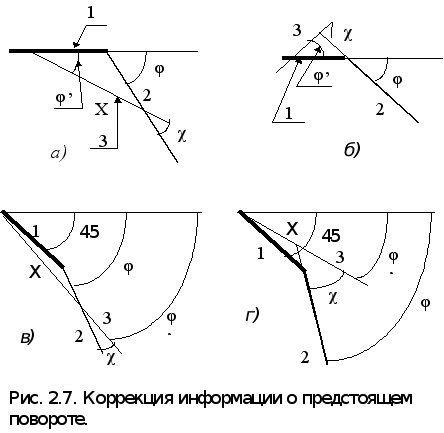
координат), и на три дискреты раньше при движении до поворота под углом к осям. Таким образом rпарр =1,875м (округлим до 2 м), а rподуглом =4,375 м (округлим до 4,5 м). В связи с тем, что реальная ориентация самосвала перед сглаживанием будет отличаться от фиксированной, требуется корректировать углы на которые должен повернуть самосвал и расстояния которые он должен проехать до поворота, что бы выйти на най денный отрезок сглаживания. В приведённых ниже рисунках (2.7 а, б, в, г) и формулах введены следующие обозначения: j’ - угол между направлениями планируемом до поворота траектории и реальной ориентацией самосвала; j - угол между направлением планируемой траектории и отрезком сглаживания; c - угол между реальным направлением самосвала и отрезком сглаживания; х - реальное расстояние до поворота; k - количество дискрет до излома; d -длина одной дискреты. Методика выбора формулы для расчёта данных коррекции приведена в таблице 2.1.
В отличие от алгоритма первичного планирования траектории (п. 2.1), алгоритм сглаживания поворотов должен быть реализован на языках высокого уровня, располагающими библиотеками математических функций и позволяющих выполнять действия над данными разных типов.
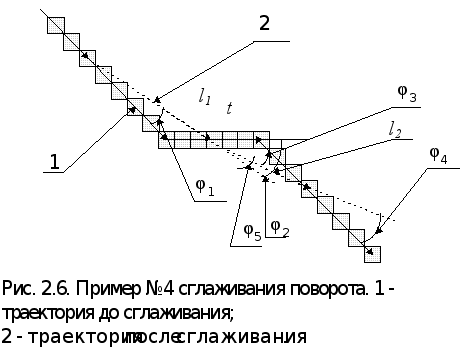
Таблица 2.1. Выбор расчётных формул для получения данных коррекции
Номер рисунка | Формула для вычисления c | Формула для вычисления х |
2.8 а | c=j-j’ | х=kd*sin(j)/sin(c) |
2.8 б | c=j+j’ | х=kd*sin(j)/sin(c) |
2.8 в | c=j-j’ | х=1.41*kd*sin(j+45)/sin(c) |
2.8 г | c=j-j’ | х=1.41*kd*sin(j-45)/sin(c) |
2.3 Планирование траектории в зоне разворота
и около точки разгрузки.
К месту разгрузки самосвал должен подъезжать задним ходом, однако максимум расстояния в местах разгрузки он проезжает передним ходом следовательно, системе автовождения самосвала требуется определить координаты точки смены направления движения и точек сопряжения разных участков траектории, кроме того система автовождения должна заранее располагать части траектории на местности, чтобы предусмотреть и избежать наезды на препятствия и въезды в зоны, не определяемые как препятствия.
Планирование смены направления в местах разгрузки самосвала имеет следующие трудности:
вероятностный характер координат и направления последнего
прямого участка движения передним ходом;
высокие требования (в связи с необходимостью повысить безопасность) к точности траектории движения задним ходом и высокие требования к точности определения координат конца участка движения задним ходом
необходимость минимизации суммарной длины отрезка до смены переднего хода на задний и длины отрезка движения задним ходом;
ограничения на предельную длину отрезка движения задним ходом;
В связи с условиями, приведёнными выше точка смены направления должна выбираться по следующим критериям:
Участок движения задним ходом должен быть кратчайшим.
Движению до и после реверса не должны мешать препятствия.
3) Точка смены направления должна быть как можно ближе к месту разгрузки.
4) Автомобиль не должен покидать пределы рабочей площадки.
С учетом выше сказанного можно сделать вывод, что геометрическим местом точек (центров самосвала) смены направления движения при подъезде к данному месту разгрузки должна быть такая кривая, которая бы имела угол наклона в точке максимально удалённой от точки разгрузки равный 0, а в точке, ближайшей к точке разгрузки - 900 . Такими свойствами обладает простейшая для анализа кривая - сегмент эллипса, расположенный между двумя его полуосями и ориентированный так, что бы одна его полуось оканчивалась на расстоянии большем или равным половине ширины самосвала от противоположной стороны площадки разгрузки и касательная, проведенная к точке эллипса, расположенной на расстоянии от точки разгрузки достаточном для исправления неточности ориентации самосвала (ограничивает малую полуось), была перпендикулярна границе рабочей площадки в точке разгрузки. Следует отметить, что после смены направления самосвал может двигаться по этому эллипсу как по заранее определённому участку траектории, используя заранее рассчитанные режимы работы двигателей и тормозной системы.
Планирование траектории начинается с построения эллипса (уравнение имеет вид (2.10)).
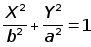 (2.10).
(2.10).
Большая его полуось (a) выбирается исходя из ширины площадки для манёвра, а малая (b) таким образом, чтобы наименьший радиус кривизны эллипса был не менее технологического радиуса. Эллипс является опорной кривой, и служит для определения точки разворота. Сопрягающая дуга является частью окружности, имеющей радиус незначительно больший технологического и строится так, чтобы она касалась эллипса и прямого отрезка, от которого и начинается планирование траектории разворота и подъезда к точке разгрузки.
Ширину малой полуоси можно определить следующим образом. Уравнение эллипса может быть приведено к виду: 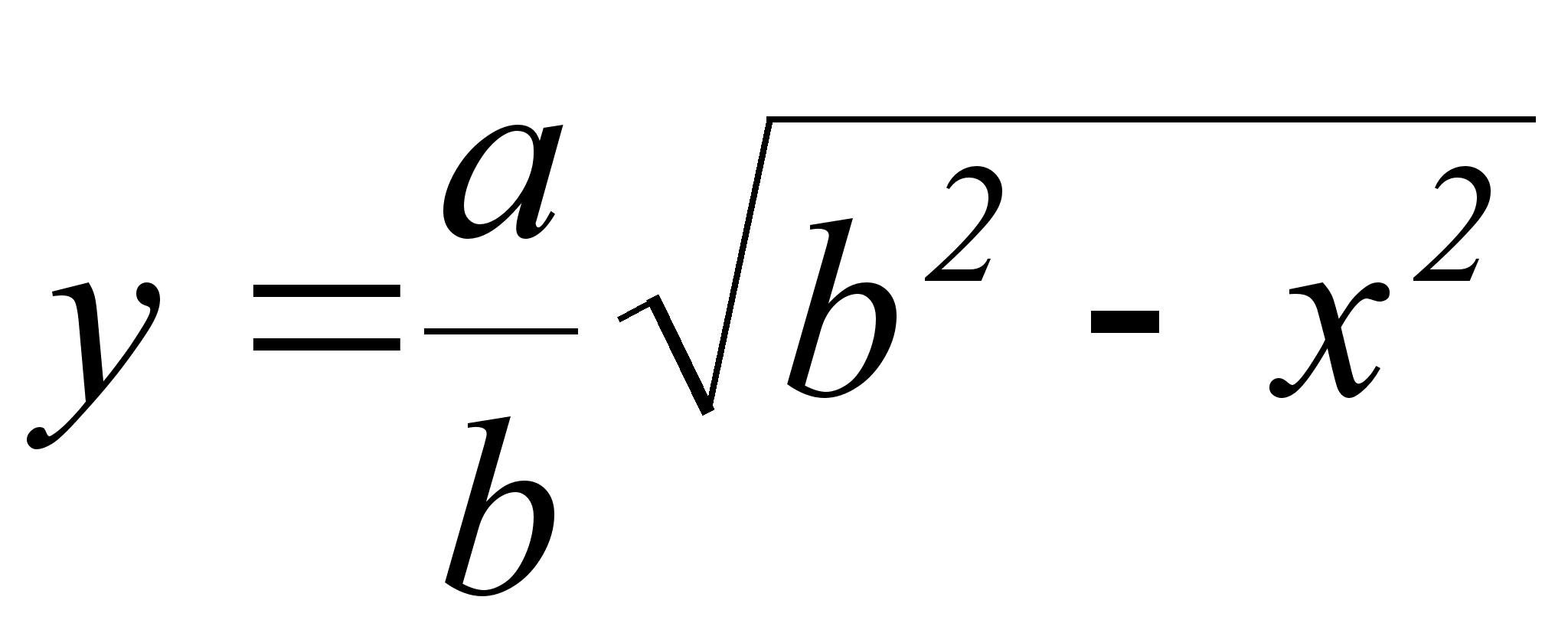
Уравнение первой производной по х будет иметь вид: 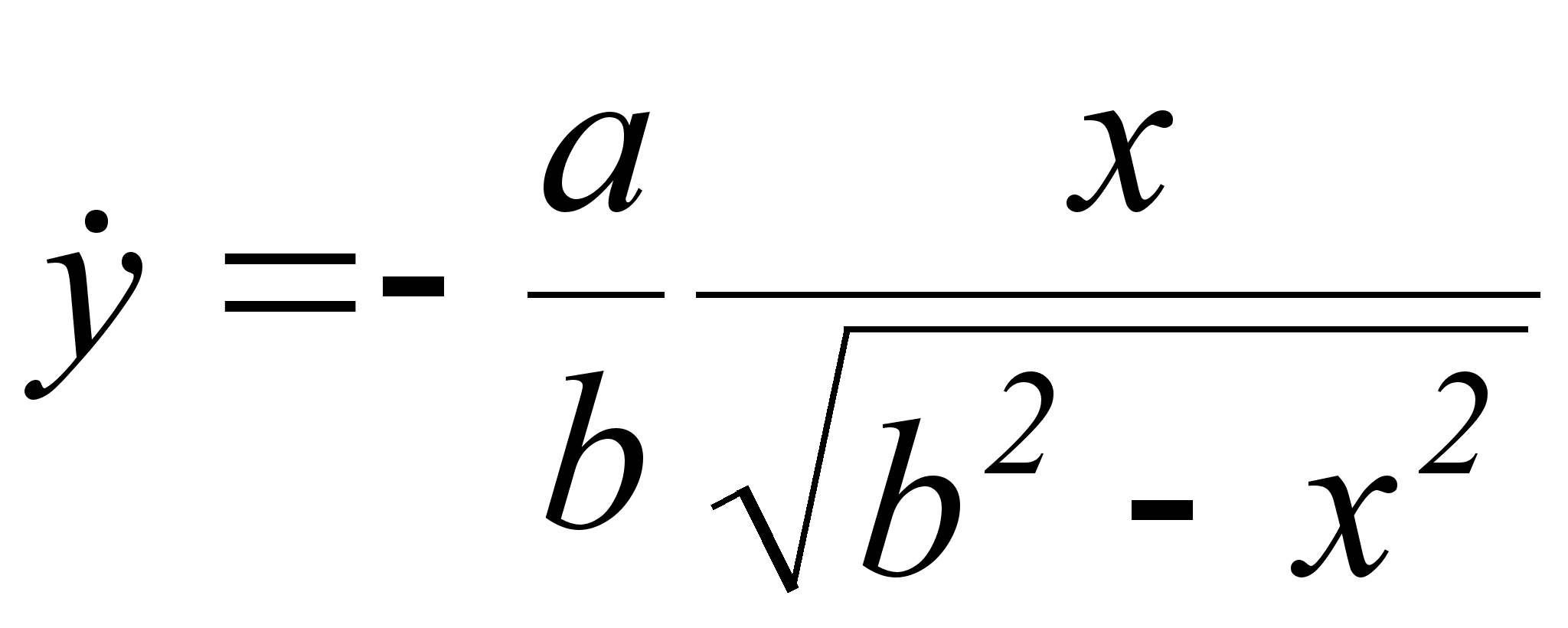 .
.
Уравнение второй производной по х будет иметь вид: 
Текущий радиус эллипса
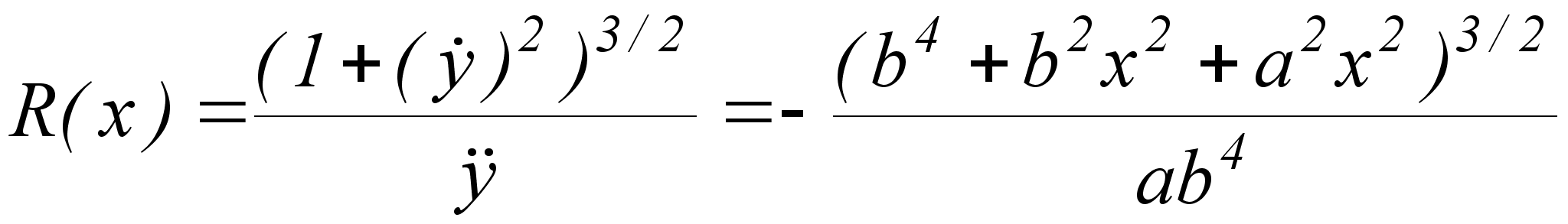 .
.
Подставив в последнее выражение х=0, получим 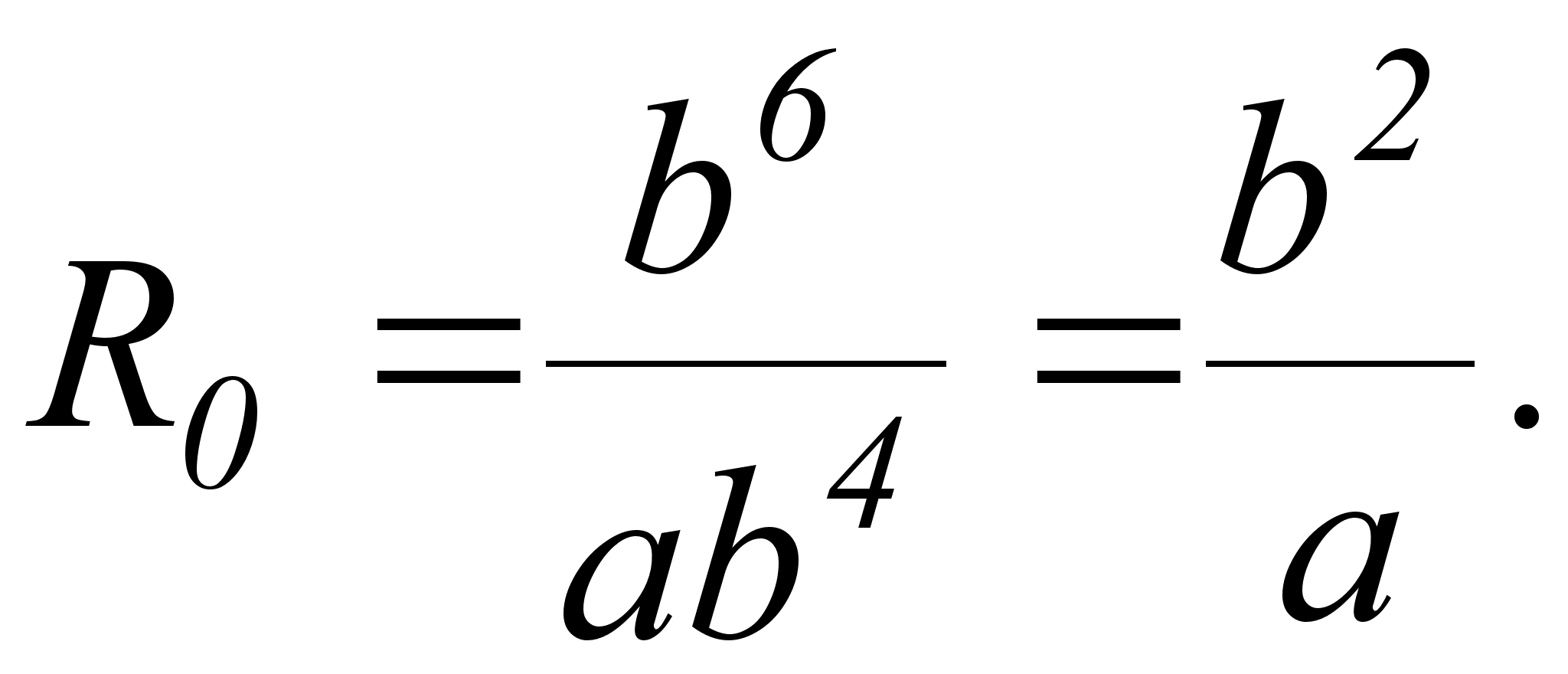
С учетом ограничения 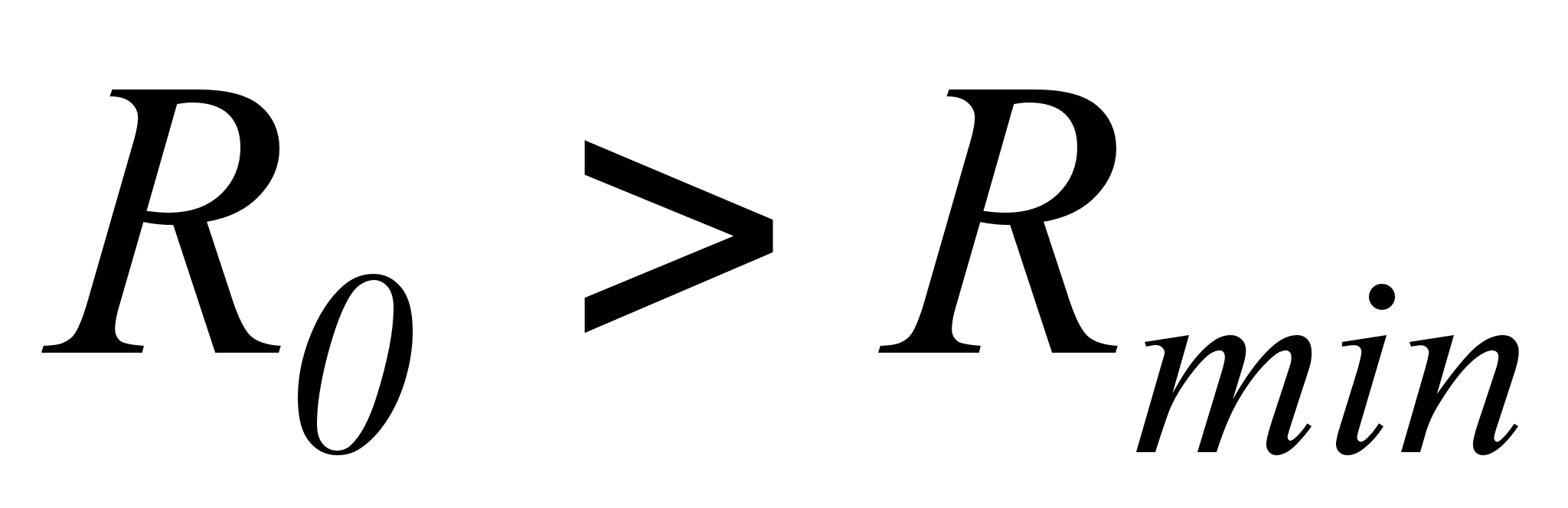 получим:
получим:
 .
.
Опорными точками этого участка траектории являются: точка А с координатами x1, y1; точка О с координатами x2, y2 и точка В с координатами x3, y3.
Геометрическим местом центров окружностей частью которых является дуга сопряжения является кривая близкая к эллипсу, имеющему уравнение 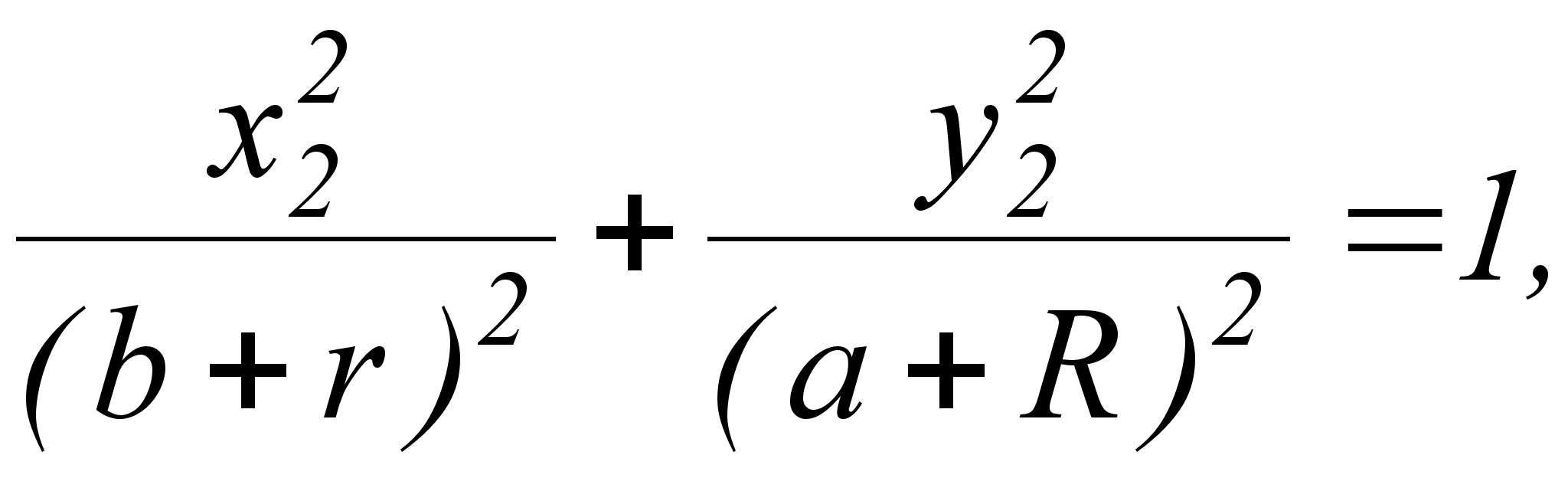 что существенно облегчает решение уравнений, связанных с определением точек перехода прямой отрезок - дуга сопряжения и дуга сопряжения - эллипс. Радиус R дуги сопряжения должен быть незначительно больше технологического чтобы компенсировать невозможность мгновенного изменения радиуса поворота самосвала.
что существенно облегчает решение уравнений, связанных с определением точек перехода прямой отрезок - дуга сопряжения и дуга сопряжения - эллипс. Радиус R дуги сопряжения должен быть незначительно больше технологического чтобы компенсировать невозможность мгновенного изменения радиуса поворота самосвала.
При развороте самосвала система ориентации должна работать как следящая и использовать в качестве задающего параметра угол разворота на задний ход jр, который для данной разгрузочной площадки есть величина постоянная.
Непосредственно перед участком смены направления движения самосвал должен двигаться по прямой. Программа должна заранее вычислить точки перехода прямая - сопрягающая окружность (А) и сопрягающая окружность - эллипс (В, точка смены направления), и по достижении указанных точек (с учётом погрешности) соответствующим образом менять задающие воздействия.
Точки сопряжения с точки зрения аналитической геометрии должны быть найдены из условий:
окружность должна иметь с прямой общую точку; производные прямой и окружности в этой точке должны быть равны;
окружность и эллипс должны иметь общую точку;
производные окружности и эллипса в этой точке должны быть равны.
Радиус (R) дуги сопряжения должен быть незначительно больше технологического чтобы компенсировать невозможность мгновенного изменения радиуса поворота самосвала.
Геометрические особенности планирования разворота и подъезда самосвала к месту разгрузки изображены на рисунке 2.8.
Приведённые на рисунке 2.8 величины можно определить по формулам 2.11 - 2.20:
A1=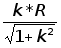 (2.11);
(2.11);
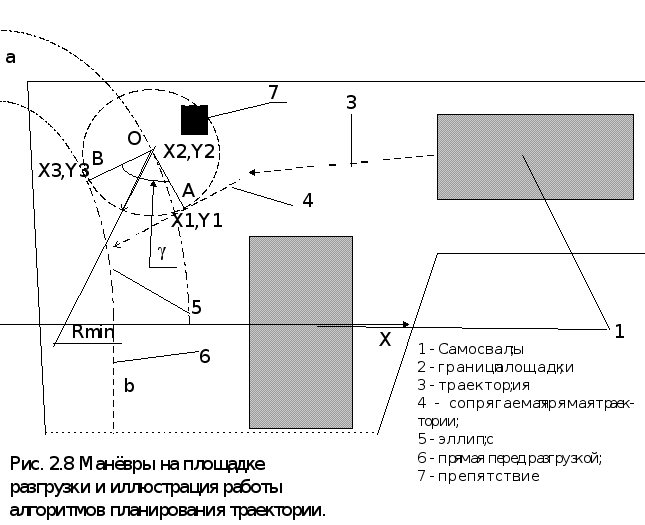
A
2=
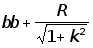
(2.12);
A=(a+R)2+k*(b+R)2 (2.13);
B=2*A1*(a+R)2-2*k*A2*(b+R)2 (2.14);
C=(a+R)2*( A12-(b+R)2 )+ A2*(b+R)2 (2.15);
X1=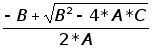 (2.16);
(2.16);
X2=X1-A1 (2.17);
Y2=k*X1-A2 (2.18);
Y3=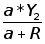 (2.19);
(2.19);
g=arccos(1-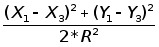 ) (2.20);
) (2.20);
В формулах 2.13 - 2.22 введены промежуточные величины (А, А1, А2, В, С), облегчающие программную реализацию вычислений.
Разработанный алгоритм должен запускаться однократно при проезде самосвалом точки с абсциссой X=b+2*R. В ходе вычислений, которые должны производиться в порядке номеров формул, будут получены координаты точек (X1, Y1) и (X3, Y3). Алгоритм позволяет реализовать автоматическое планирование участка смены направления движения на бортовой ЭВМ системы автовождения карьерного самосвала. Относительная простота формул позволит осуществлять вычисления за минимальное время.
Как и алгоритм сглаживания, алгоритм подъезда к точке разгрузки должен быть реализован на языках высокого уровня.
2.4 Планирование выезда самосвала
из зоны разгрузки.
Планирование траектории выезда самосвала из зоны разгрузки отличается от планирования подъезда к месту разгрузки только отсутствием участка смены направления движения. Планирование траектории также должно состоять из первичного и вторичного.
Следует отметить, что траектория движения должна быть прижата к стороне, противоположной от той на которой расположены места разгрузки для того, чтобы не мешать манёврам самосвалов, которым ещё предстоит разгрузиться. Для алгоритма первичного планирования (п 2.1) это выливается лишь во введении дополнительных критериев оценки. Сглаживание поворотов (вторичное планирование) должно выполнятся по аналогичным (п. 2.2) формулам.
В связи со значительным изменением после разгрузки динамических свойств самосвала, данные для расчёта заданий на ускорение, торможение и поворот должны быть измерены и рассчитаны заново. Программе планирования траектории должна быть передана информация о зависимости тормозного пути от скорости и радиуса поворота от скорости. Информация о выезде из зоны манёвров может быть передана от ДЭВМ или заранее заложена в память как и карта местности.
3 Навигация большегрузного
карьерного автосамосвала по счислению.
В связи с невозможностью точно измерять мгновенное положение автомобиля, а также высокой чувствительностью к помехам системы радионавигации карьерного самосвала, необходимо обеспечить программное дублирование определения параметров его положения на местности (координаты и угол поворота относительно неподвижной системы координат рабочей площадки). Указанные параметры особенно важны во время планирования траектории и выполнения поворотов, а также при выдаче команд на смену направления движения, при обнаружении выезда самосвала в точку с заданными координатами при планировании подъезда к точке разгрузки.
Для успешного функционирования алгоритма требуется определять мгновенное значение реального радиуса поворота. Реальный радиус поворота позволяют определить датчики поворота колёс на заданный угол, установленные на каждом колесе и работающие независимо друг от друга. Если между импульсами датчика, выдаваемыми им после поворота колеса на элементарный угол, накапливать импульсы высокой частоты, то по простым формулам можно определить радиус поворота (формула (3.1)):
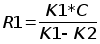 (3.1).
(3.1).
В формуле: К1 - количество импульсов, пришедших между сигналами от датчика поворота от заднего колеса, ближнего к центру поворота, С - ширина колеи, К2 - количество импульсов, пришедших между сигналами датчика поворота от заднего колеса, дальнего от центра поворота.
Выберем частоту импульсов от датчика по следующим соображениям. Алгоритм планирования траектории должен запускаться после проезда самосвалом одной дискреты. Длина одной дискреты 1,25 м, наибольшая скорость движения самосвала 15 км/ч, получим, время после которого данные о положении самосвала должны быть готовы: t=1.25(м)/(15000(км/ч)/3600(с/ч))=0.3 с. Учитывая специфику групповой работы датчиков уменьшим время ещё в 3 раза (запас времени на расчёты) и получим t=0.1 с. Определим, на какой угол (l) повернётся за это время колесо самосвала (и шаг угловой сетки на датчике): l=0,1(с)*4,167(м/с)/3(м)=0,1389 рад=7,950
Вместе с этим смотрят:
11-этажный жилой дом с мансардой
14-этажный 84-квартирный жилой дом
16-этажный жилой дом с монолитным каркасом в г. Краснодаре
180-квартирный жилой дом в г. Тихорецке
2-этажный 3-секционный 18-квартирный жилой дом в г. Мирном