Техническое зрение роботов

1.ВВЕДЕНИЕ

С целью классификации методов и подходов, используемых в сиВнстемах технического зрения, зрение разбито на три осВнновных подкласса: зрение низкого, среднего и высокого уровВнней. Системы технического зрения низкого уровня предназначены для обработки информаВнции с датчиков очувствления.

Эти системы можно отнести к классу ВлинтеллектуальныхВ» машин, если они обладают следующими признаками (признаВнками интеллектуального поведения):

1) возможностью выделения существенной информации из множества независимых признаков;

2) способностью к обучению на примерах и обобщению этих знаний с целью их применения в новых ситуациях;

3) возможностью восстановления событий по неполной инВнформации;

4) способностью определять цели и формулировать планы для достижения этих целей.

Создание систем технического зрения с такими свойствами для ограниченных видов рабочего пространства в принципе возВнможно, но характеристики таких систем далеки от возможностей человеческого зрения. В основе технического зрения лежит аналитическая формализация, направленная на решение конкретВнных задач. Машины с сенсорными характеристиками, близкими к возможностям человека, по-видимому, появятся еще не скоро. Однако отметим, что копирование природы не является единстВнвенным решением этой проблемы. Читателю наверняка известны ранние экспериментальные образцы аэропланов с машущими крыльями и другими особенностями полета птиц. Современное решение задачи о полете в пространстве в корне отличается от решений, подсказанных природой. По скорости и достижимой высоте самолеты намного превосходят возможности птиц.

Системы технического зрения среднего уровня связаны с задачами сегментации, описания и распознавания отдельных объектов. Эти задачи охватывают множество подходов, осВннованных на аналитических представлениях. Системы техничеВнского зрения высокого уровня решают проблемы, рассмотренные выше. Для более ясного понимания проблем технического зреВнния высокого уровня и его связи с техническим зрением низкого и среднего уровней введем ряд ограничений и упростим решаеВнмую задачу.


2.СЕГМЕНТАЦИЯ

Сегментацией называется процесс подразделения сцены на составляющие части или объекты. Сегментация является одним из основных элементов работы автоматизированной системы технического зрения, так как именно на этой стадии обработки объекты выделяются из сцены для дальнейшего распознавания и анализа. Алгоритмы сегментации, как правило, основываются на двух фундаментальных принципах: разрывности и подобии. В первом случае основной подход основывается на определении контуров, а во втором тАФ на определении порогового уровня и расширении области. Эти понятия применимы как к статичеВнским, так и к динамическим (зависящим от времени) сценам. В последнем случае движение может служить мощным средстВнвом для улучшения работы алгоритмов сегментации.

2.1.Проведение контуров и определение границы

Методы - вычисление градиента, пороговое разделение - определяют разрывы в интенсивности представления образа объекта. В идеальном слуВнчае эти методы определяют пикселы, лежащие на границе межВнду объектом и фоном. На практике данный ряд пикселов редко полностью характеризует границу из-за шума, разрывов на граВннице вследствие неравномерной освещенности и других эффекВнтов, приводящих к размытию изображения. Таким образом, алВнгоритмы обнаружения контуров сопровождаются процедурами построения границ объектов из соответствующих последовательВнностей пикселов. Ниже рассмотрено несколько методик, приВнгодных для этой цели.

2.1.1.Локальный анализ.

Одним из наиболее простых подходов соединения точек контура является анализ характеристик пикВнселов в небольшой окрестности (например, в окрестности разВнмером 3 X 3 или 5 X 5) каждой точки (х, у) образа, который уже подвергся процедуре обнаружения контура. Все точки, явВнляющиеся подобными (определение критерия подобия дано ниже), соединяются, образуя границу из пикселов, обладающих некоторыми общими свойствами.

При таком анализе для установления подобия пикселов конВнтура необходимо определить:

1 ) величину градиента, требуемого для построения контурного пиксела,

2) направление градиенВнта.

Первая характеристика обозначается величиной G{f(x, у)].

Таким образом, пиксел контура с координатами (х', у') подобен по величине в определенной ранее окрестности (х, у) пикселу с координатами (х, у), если справедливо неравенство

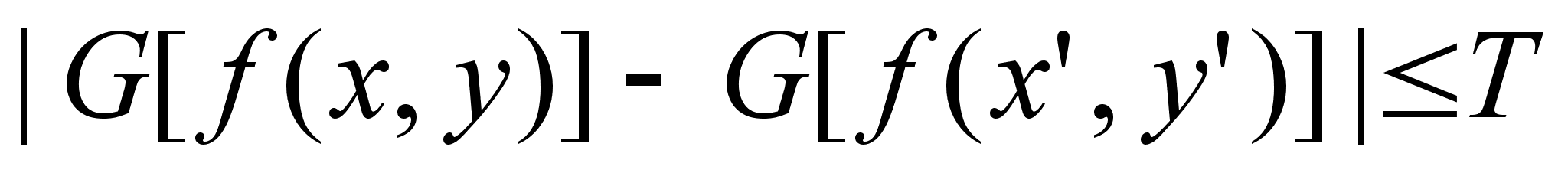
где ТтАФпороговое значение.

Направление градиента устанавливается по углу вектора градиента, определенного в уравнении

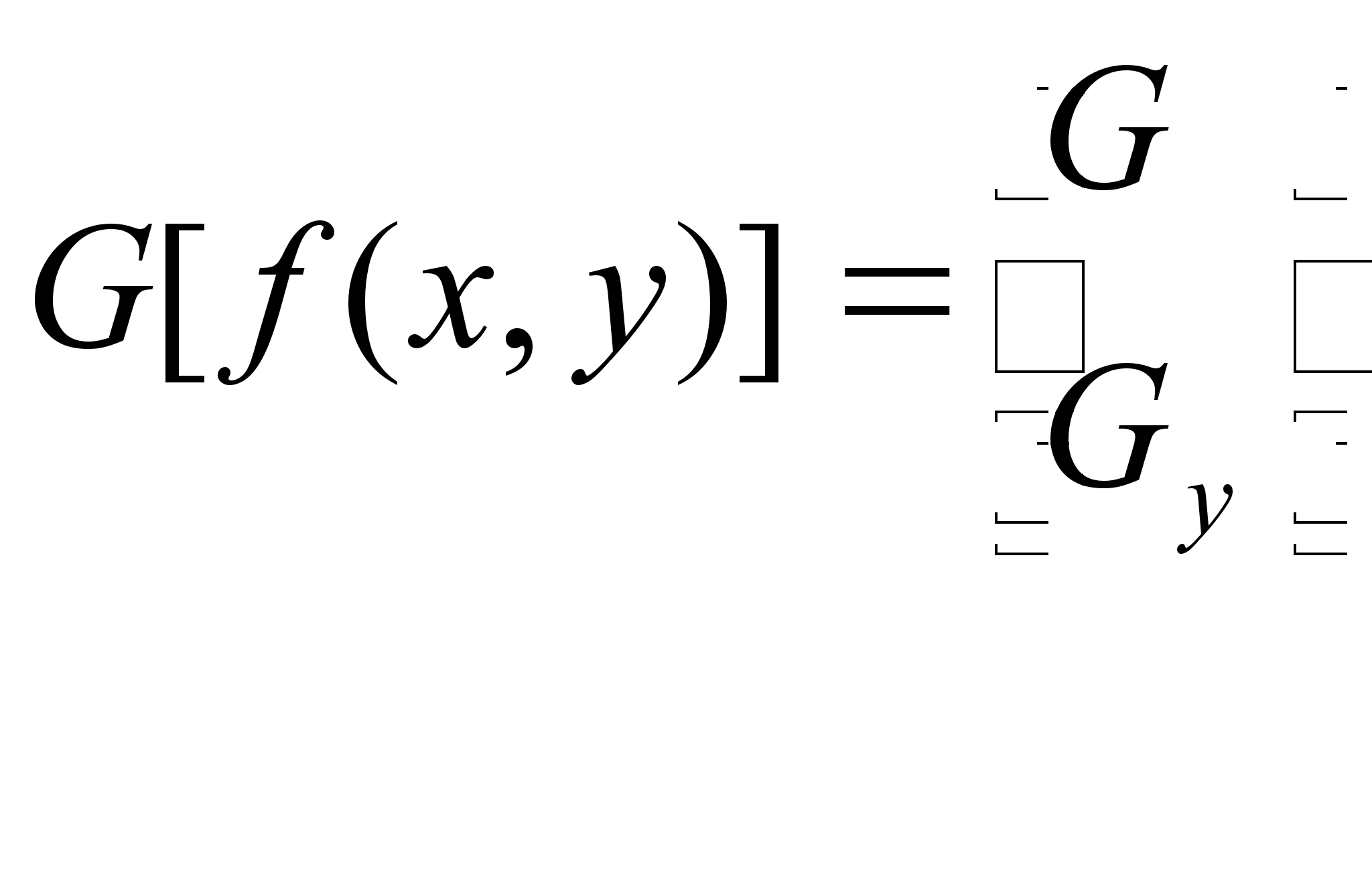
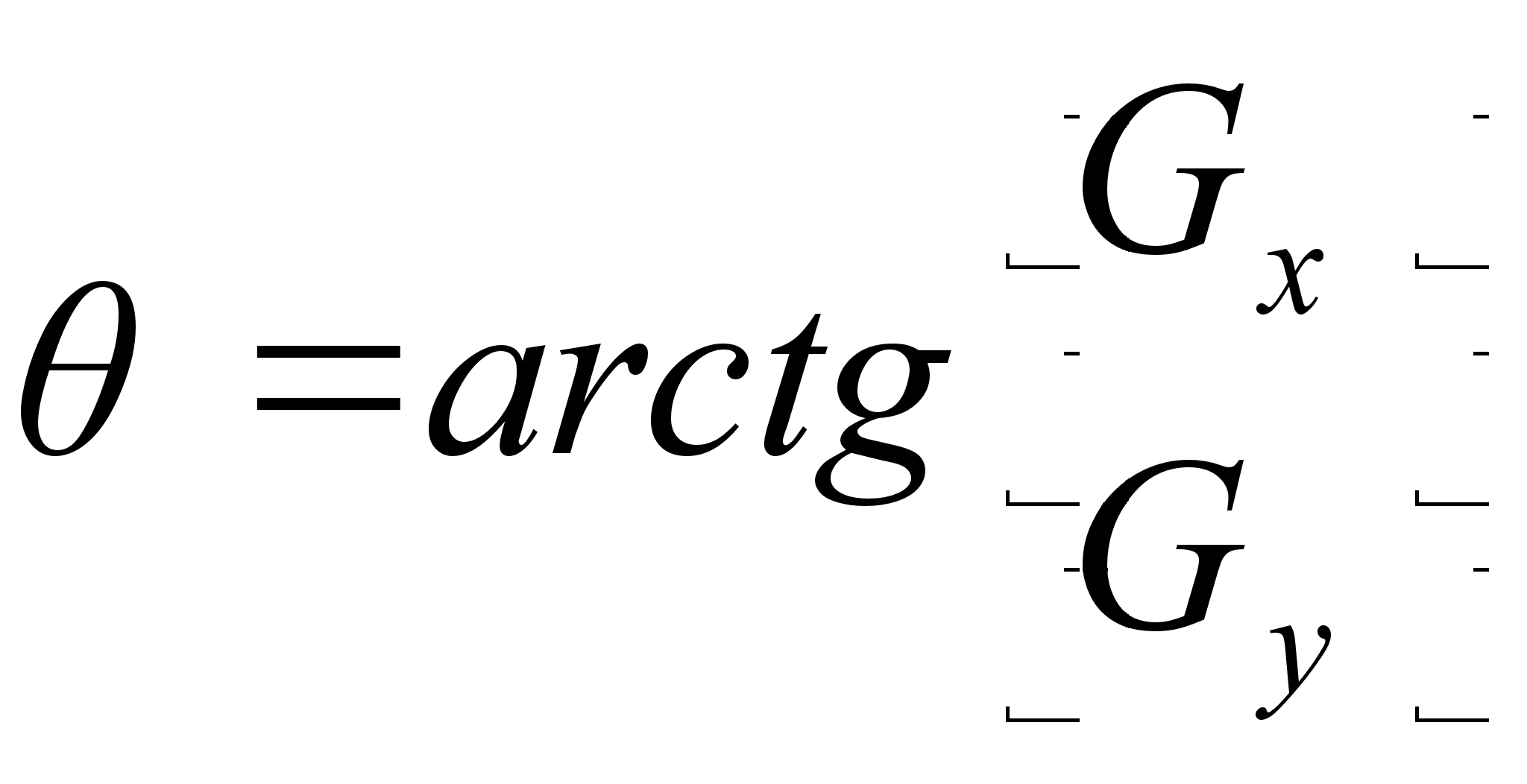
где тАФугол (относительно оси х), вдоль которого скорость изменения имеет наибольшее значение. Тогда можно сказать, что угол пиксела контура с координатами {х', у') в некоторой окрестности (х, у) подобен углу пиксела с координатами {х, у) при выполнении следующего неравенства:

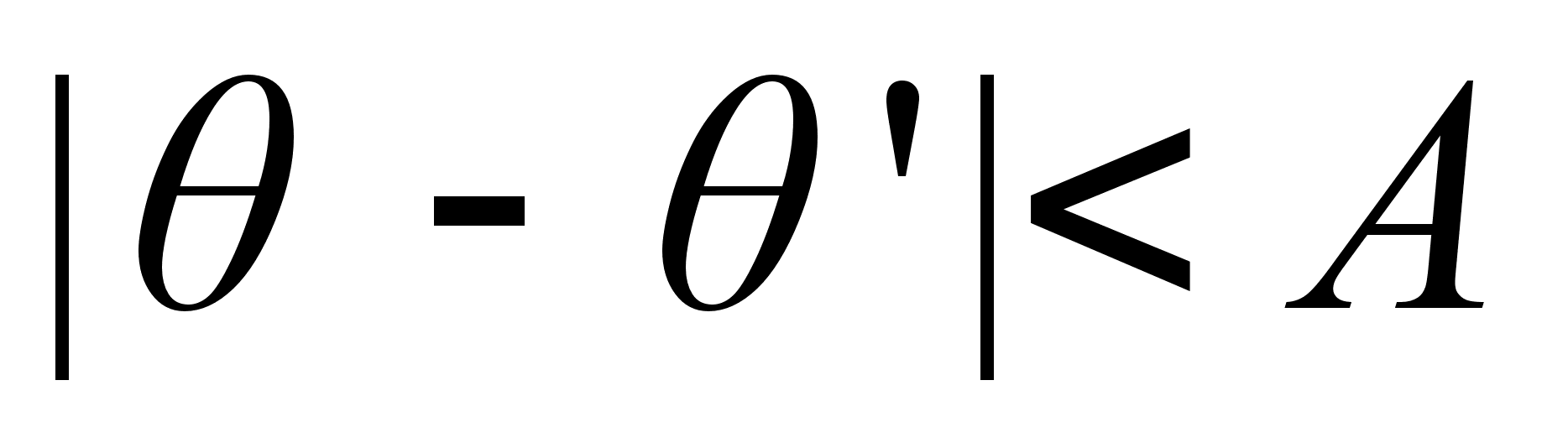
где АтАФпороговое значение угла. Необходимо отметить, что наВнправление контура в точке {х, у) в действительности перпендиВнкулярно направлению вектора градиента в этой точке. Однако для сравнения направлений неравенство дает эквивалентВнные результаты.

Основываясь на этих предположениях, мы соединяем точку в некоторой окрестности (х, у) с пикселом, имеющим коордиВннаты (х, у), если удовлетворяются критерии по величине и направлению. Двигаясь от пиксела к пикселу и представляя каждую присоединяемую точку как центр окрестности, процесс повторяется для каждой точки образа. Для установления соотВнветствия между уровнями интенсивности освещения и последоВнвательностями пикселов контура применяется стандартная бибВнлиотечная процедура.

Цель состоит в определении размеров прямоугольниВнков, с помощью которых можно построить качественное изобраВнжение. Построение таких прямоугольников осуществляется в реВнзультате определения строго горизонтальных и вертикальных контуров. Дальнейший процесс состоял в соединении сегментов контура, разделенных небольшими промежутками, и в объединении отдельных коротВнких сегментов.

2.1.2.Глобальный анализ с помощью преобразования Хоуга.

РасВнсмотрим метод соединения граничных точек путем определения их расположения на кривой специального вида. Первоначально предполагая, что на плоскости ху образа дано п точек, требуется найти подпоследовательности точек, лежащих на прямых линиях. Одно из возможных решений состоит в построении всех линий, проходящих через каждую пару точек, а затем в нахожВндении всех подпоследовательностей точек, близких к определенВнным линиям. Задача, связанная с этой процедурой, заключается в нахождении п(птАФ 1)/2 ~ п2 линий и затем в осуществлении п[п(птАФ1)]/2 ~ п3 сравнений каждой точки со всеми линиями. Этот процесс трудоемок с вычислительной точки зрения за исВнключением самых простых приложений.

Данную задачу можно решить по-другому, применяя подход, предложенный Хоугом и называемый преобразованием Хоуга. Рассмотрим точку (хi yi) и общее уравнение прямой лиВннии у:= аxi + i. Имеется бесконечное число линий, проходящих через точку (хi yi), но все они удовлетворяют уравнению у:= аxi + i при различных значениях а и b. Однако, если мы заВнпишем это уравнение в виде b = -хiа + yi и рассмотрим плоВнскость аb (пространство параметров), тогда мы имеем уравнеВнние одной линии для фиксированной пары чисел (хi yi). Более того, вторая точка (хj, уj) также имеет в пространстве параВнметров связанную с ней линию, которая пересекает другую лиВннию, связанную с точкой (хi yi) в точке (а', b’), где значения а' и b’тАФпараметры линии, на которой расположены точки (хi yi) и (хj, уj) в плоскости ху. Фактически все точки, расположенВнные на этой линии, в пространстве параметров будут иметь лиВннии пересечения в точке (а', b’).

Вычислительная привлекательность преобразования Хоуга заключается в разделении пространства параметров на так наВнзываемые собирающие элементы , где (aмакс, амин) и (bмакс, bмин)тАФдопустимые величины параметров линий. Собирающий элемент A (i, j) соответствует площади, связанной с коВнординатами пространства параметров (аi, j). Вначале эти элементы считаются равными нулю. Тогда для каждой точки (xk, уk) в плоскости образа мы полагаем параметр а равным кажВндому из допустимых значений на оси а и вычисляем соответстВнвующее b, используя уравнение = -хk + yk Полученное значение b затем округляется до ближайшего допустимого знаВнчения на оси b. Если выбор aр приводит к вычислению bq, мы полагаем А(р, q) ==А(р, q) + 1. После завершения этой проВнцедуры значение М в элементе A (i, j) соответствует М точкам в плоскости xy, лежащим на линии y=aix+b. Точность расВнположения этих точек на одной прямой зависит от числа разВнбиений плоскости аb. Отметим, что, если мы разбиваем ось а на К частей, тогда для каждой точВнки (xk, уk) мы получаем К знаВнчений b, соответствующих К возВнможным значениям а. ПоскольВнку имеется п точек образа, проВнцесс состоит из пК вычислительВнных операций. Поэтому привеВнденная выше процедура линейна относительно п и имеет меньшее число вычислительных операВнций, чем процедура, описанная выше, если К<=п.

Проблема, связанная с предВнставлением прямой линии уравВннением у = ах + b, состоит в том, что оба параметра а и стремятся к бесконечности, если линия принимает вертикальВнное положение. Для устранения этой трудности используется нормальное представление прямой линии в виде

xcos+ysin=.

Это представление для построения таблицы собирающих элементов используется так же, как метод, изложенный выше, но вместо прямых линий мы имеем синусоидальные кривые в плоскости . Как и прежде, М точек, лежащих на прямой xcosi+уsini == i, соответствуют М синусоидальным кривым, котоВнрые пересекаются в точке (i,i) пространства параметров. Если используется метод возрастания и нахождения для него соотВнветствующего , процедура дает М точек в собирающий элемент А (i, j), связанный с точкой (i,i).

2.1.3.Глобальный анализ с помощью методов теории графов.

Изложенные выше методы основаны на задании последовательности точек контура, полученных в результате градиентного преВнобразования. Этот метод редко применяется для предварительВнной обработки данных в ситуациях, характеризуемых высоким уровнем шума, вследствие того, что градиент является произВнводной и усиливает колебания интенсивности. Рассмотрим глоВнбальный подход, основанный на представлении сегментов конВнтура в виде графа и поиске на графе пути наименьшей стоимости, который соответствует значимым контурам. Этот подход представляет приближенный метод, эффективный при наличии шума. Как и следует ожидать, эта процедура значительно сложВннее и требует больше времени обработки, чем методы, изложенВнные выше.

Сначала дадим несколько простых определений. Граф G = (N, А) представляет собой конечное, непустое множество вершин N вместе с множеством А неупорядоченных пар различВнных элементов из N. Каждая пара из А называется дугой.

Граф, в котором дуги являются направленными, называется наВнправленным графом. Если дуга выходит из вершины ni, к верВншине пj, тогда пj называется преемником вершины ni. В этом случае вершина i называется предшественником вершины пj. Процесс идентификации преемников каждой вершины назыВнвается расширением этой вершины. В каждом графе опредеВнляются уровни таким образом, чтобы нулевой уровень состоял из единственной вершины, называемой начальной, а последний уровеньтАФиз вершин, называемых целевыми. Каждой дуге (niпj) приписывается стоимость c(niпj). Последовательность верВншин п1, n2, .., nk, где каждая вершина ni является преемником вершины ri-1, называется путем от i к пk, а стоимость пути определяется формулой

.

Элемент контура мы определим как границу между двумя пикВнселами р и q. В данном контексте под контуром пониВнмается последовательность элементов контура.


2.2.Определение порогового уровня

Понятие порогового уровня (порога) тест вида

Т = Т [х, у, р (х, у), f (х, у)],

где f(x, у) тАФинтенсивность в точке (х, у), р(х, у)тАФнекоторое локальное свойство, определяемое в окрестности этой точки. Пороговое изображение дается следующим выражением:


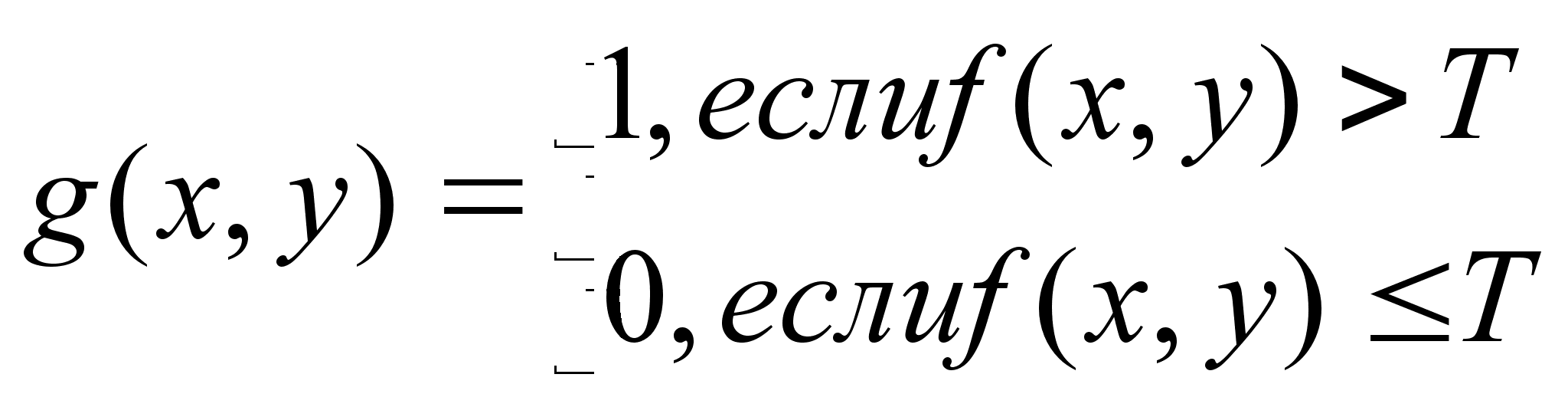
так что пикселы в g(x, у), имеющие значение 1, соответствуют объектам, а пикселы, имеющие значение 0, соответствуют фону. В уравнении предполагается, что интенсивность объекВнтов больше интенсивности фона. Противоположное условие поВнлучается путем изменения знаков в неравенствах.

2.2.1.Глобальные и локальные пороги.

Если значение Т в уравнеВннии зависит только от f(x, у), то, порог называется глобальным. Если значение Т зависит как от f(x, у), так и от р(х, у), порог называется локальным. Если, кроме того, Т зависит от пространственных координат х а у, в этом случае он называется динамическим порогом.

Глобальные пороги применяются в ситуациях, когда имеется явное различие между объектами и фоном и где освещенность достаточно однородна. Методы обратной и структурированной освещенности, обычно дают изображеВнния, которые могут быть сегментированы путем применения глобальных порогов. Но, как правило, произвольное освещение рабочего пространства приводит к изображениям, которые, если исходить из определения порогового уровня, требуют локального анализа для компенсации таких эффектов, как неоднородность освещения, тени и отражение.

Ниже мы рассмотрим ряд методов для выбора порогов, исВнпользуемых при сегментации. Хотя некоторые из них могут приВнменяться для выбора глобального порога, они обычно испольВнзуются в ситуациях, требующих анализа локального порога.

2.2.2.Выбор оптимального порога.

Часто рассматривают гистоВнграмму, состоящую из суммы значений функции плотности веВнроятности. В случае бимодальной гистограммы аппроксимируюВнщая ее функция дается уравнением

p(z)=P1p1(z)+P2p2(z),

где интенсивность zтАФслучайная переменная величина, p1(z) и p2(z)тАФфункции плотности вероятности, a P1 и P2 тАУ априорные вероятности. В данном случае априорные вероятности означают появление двух видов уровней интенсивности на образе. Полная гистограмма может быть аппроксимирована суммой двух функций плотности вероятности. Если известно, что объект состоит из светлых пиксеВнлов и они занимают 20 % площади образа, то Pi ==0,2. НеобхоВндимо, чтобы

Р1+Рг=1.

В данном случае это означает, что на остальную часть образа приходится 80 % пикселов фона. Введем две следующие функции от z:

d1(z)=P1p1(z),

d2(z)=P1p1(z).

Из теории принятия решений известно, что средняя ошибка определения пиксела объекта в качестве фона (и наВноборот) минимизируется с помощью следующего правила: расВнсматривая пиксел со значением интенсивности z, мы подставВнляем это значение z в уравнения (8.2-13) и (8.2-14). Затем мы определяем пиксел как пиксел объекта, если d1(z) >d2(z), или как пиксел фона, если d2(2) > d1(z). Тогда оптимальный порог определяется величиной z, для которой d1{z)=d2(z). Таким образом, полагая в уравнениях z=T, полуВнчаем, что оптимальный порог удовлетворяет уравнению

P1р1(T)=P2p2(T).


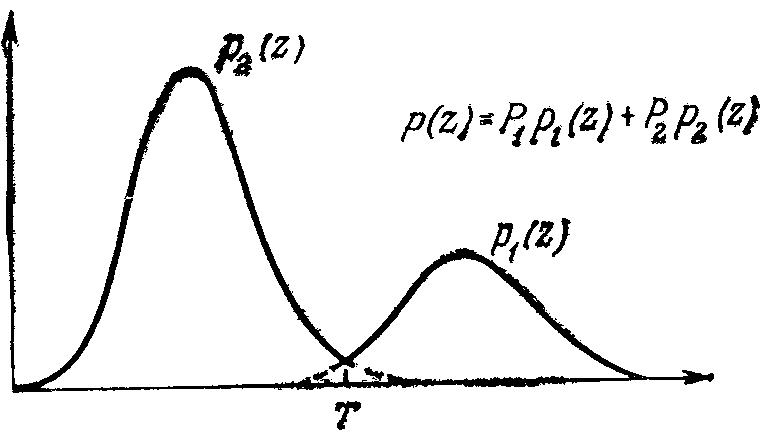
рис. Гистограмма интенсивности (а) и ее аппроксимация в виде тАвсуммы двух функций плотности вероятности (б).


Итак, если известны функциональные зависимости p1(z) и р2(г),. это уравнение можно использовать для нахождения оптимальВнного порога, который отделяет объекты от фона. Если этот порог известен, уравнение может быть использовано для сегментации данного образа.

2.2.3.Определение порогового уровня на основе характеристик границы.

Одним из наиболее важных аспектов при выборе поВнрогового уровня является возможность надежно идентифицироВнвать модовые пики для данной гистограммы. Это важно при автоматическом выборе порогового уровня в ситуациях, когда характеристики образа меняются вследствие большого разброса интенсивности. Из изложенного выше очевидно, что возможность выбора ВлхорошегоВ» порогового уровня может быть существенно увеличена в случае, если пики гистограмм являются высокими, узкими, симметричными и разделены глубокими провалами.

Одним из подходов для улучшения вида гистограмм является рассмотрение только тех пикселов, которые лежат на границе (или около нее) между объектами и фоном. Одно из очевидных улучшений состоит в том, что этот подход позволяет получать гистограммы менее зависимыми от отношения между объектом и фоном. Например, гистограмма интенсивности образа, составВнленного из маленького объекта на большой площади постоянВнного фона, определялась бы большим пиком вследствие концентВнрации пикселов фона. С другой стороны, результирующие гистоВнграммы имели бы пики с более сбалансированными высотами, если бы рассматривались пикселы, лежащие только на (или около) границе между объектом и фоном. Кроме того, вероятВнность расположения пиксела на границе объекта практически равна вероятности того, что он лежит на границе фона, что улучшает симметрию гистограммных пиков. Окончательно, как показано ниже, использование пикселов, которые удовлетвоВнряют некоторым простым критериям, основанным на операторах градиента и Лапласа, приводит к увеличению провалов между пиками гистограммы.

Выше мы неявно подразумевали, что граница между объекВнтами и фоном известна. Очевидно, что во время проведения сегВнментации эта информация отсутствует, поскольку нахождение раздела между объектами и фоном является окончательной целью приведенной здесь процедуры. Однако, что, вычислив градиент пиксела, можно определить, леВнжит ли он или не лежит на контуре. Кроме того, лапласиан моВнжет дать информацию о том, лежит ли данный пиксел на темной (т. е. фон) или светлой (объект) стороне контура. С внутренней стороны идеального контура лапласиан равен нулю, поэтому на практике можно ожидать, что провалы гистограмм, образованных пикселами, выбранными по критерию градиент/лапласиан, будут располагаться достаточно редко и иметь желаемую высоту.

Градиент G[f(x,y)] любой точки образа и лапласиан L[f{x, у)]. Эти два свойства можно использовать для форВнмирования трехуровнего образа:



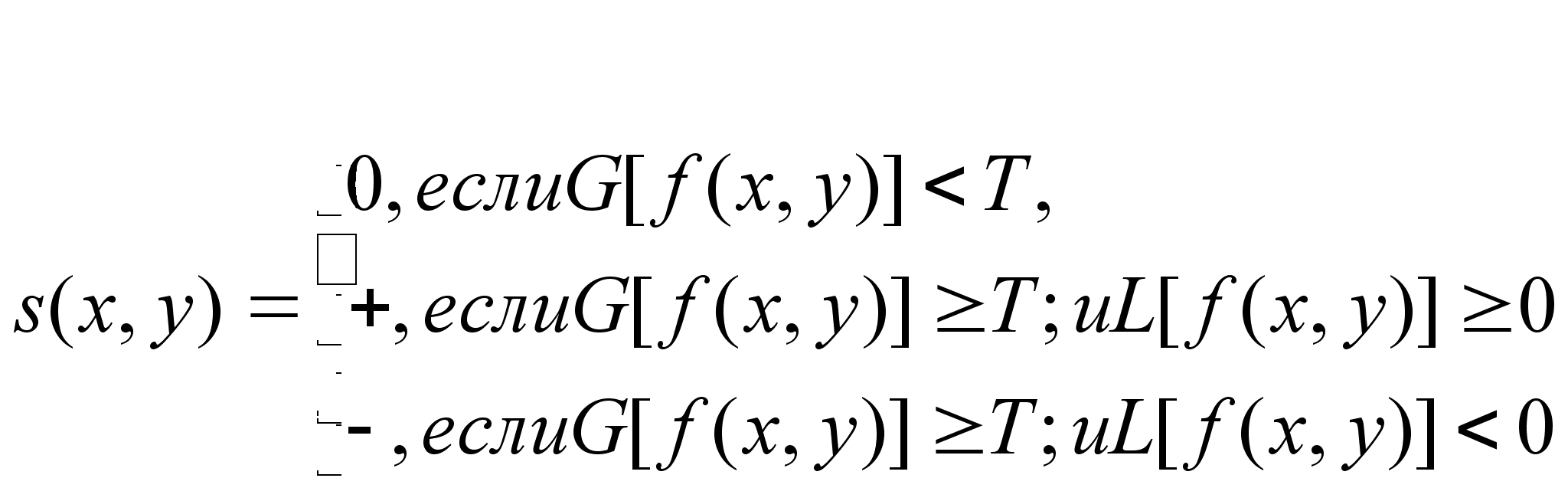
(где символы 0, +, - представляют три различных уровня освеВнщенности, а ТтАФпороговый уровень. Предположим, что темный объект располагается на светлом фоне, тогда применение уравнения дает образ s(x, у), в котором все пикселы, не лежащие на контуре (для них значеВнние G[f (х, у)] меньше Т, помечены 0, все пикселы на темной стороне контура помечены + и все пикселы на светлой стороне контура помечены тАФ. Для светлого объекта на темном фоне символы + и - в уравнении (8.2-24) меняются местами.

Только что изложенная процедура может применяться для создания сегментированного, бинарного образа, в котором 1 соВнответствует объектам, представляющим интерес, и 0тАФфону. Отметим, что перемещение (вдоль горизонтальных или верВнтикальных линий сканирования) от светлого фона к темному объекту должно характеризоваться заменой знака - фона на -1- объекта s(x, у). Внутренняя область объекта состоит из пикселов, помеченных либо 0 либо +. Окончательно перемещение от объекта к фону характеризуется заменой знака + на тАФ. Таким образом, горизонтальные или вертикальные линии сканирования, содержащие части объекта, имеют следующую структуру:

(..)(-, +)(0 или +)(+, -)(тАвтАвтАв),

где (..) является произвольной комбинацией +, - или 0. Остальные скобки содержат точки объекта и помечены 1. Все другие пикселы вдоль той же линии сканирования помечаются 0, за исключением всех последовательностей из (0 или +), ограВнниченных (-, +) и (+, -).

2.2.4.Определение порогового уровня, основанное на нескольких переменных.

Изложенные выше методы связаны с определением порогового уровня для единстВнвенного переменного значения интенсивности. В некоторых приложениях можно испольВнзовать более одной переменВнной для характеристики каждоВнго пиксела образа, увеличивая таким образом не только стеВнпень различия между объекВнтом и фоном, но и между самиВнми объектами. Одним из наиВнболее значимых примеров являВнется цветное зрение, где испольВнзуются красные, зеленые и голубые компоненты (КЗГ) для формирования составноВнго цветного образа. В этом случае каждый пиксел характеризуется тремя переменными и это позволяет строить трехмерную гистограмму. Основная процедура та же, что и для одной переменной. Пусть, например, даны три 16-уровневых изображения, соответствующие КЗГ компонентам датчика цвета. Сформируем кубическую решетку 16х16х16 и поместим в каждый элемент пикселы, КЗГ комВнпоненты которых имеют интенсивности, соответствующие коорВндинатам, определяющим положение этого элемента. Число тоВнчек в каждом элементе решетки может быть затем разделено на общее число пикселов образа для формирования нормированной гистограммы.

Теперь выбор порога заключается в нахождении групп точек в трехмерном пространстве, где каждая ВлкомпактнаяВ» группа аналогична основной моде гистограммы одной переменной. НаВнпример, предположим, что мы ищем две значимые группы точек данной гистограммы, где одна группа соответствует объекту, а другаятАФфону. Принимая во внимание, что теперь каждый пикВнсел имеет три компоненты и может быть рассмотрен как точка трехмерного пространства, можно сегментировать образ с поВнмощью следующей процедуры. Для каждого пиксела образа вычисляется расстояние между этим пикселом и центром кажВндой группы. Тогда, если пиксел располагается рядом с центром группы точек объекта, мы помечаем его 1; в противном случае мы помечаем его 0. Это понятие легко распространить на больВншую часть компонентов пиксела и соответственно на большую часть групп. Основная сложность состоит в том, что определение значимых групп, как правило, приводит к довольно сложной задаче, поскольку число переменных возрастает.


2.3.Областно-ориентированная сегментация

2.3.1.Основные определения.

Целью сегментации является раздеВнление образа на области. Рассмотрим методы сегменВнтации, основанные на прямом нахождении областей.

Пусть R тАФ область образа. Рассмотрим сегментацию как процесс разбиения R на подобластей R1, R2, .., Rn, так что

1.

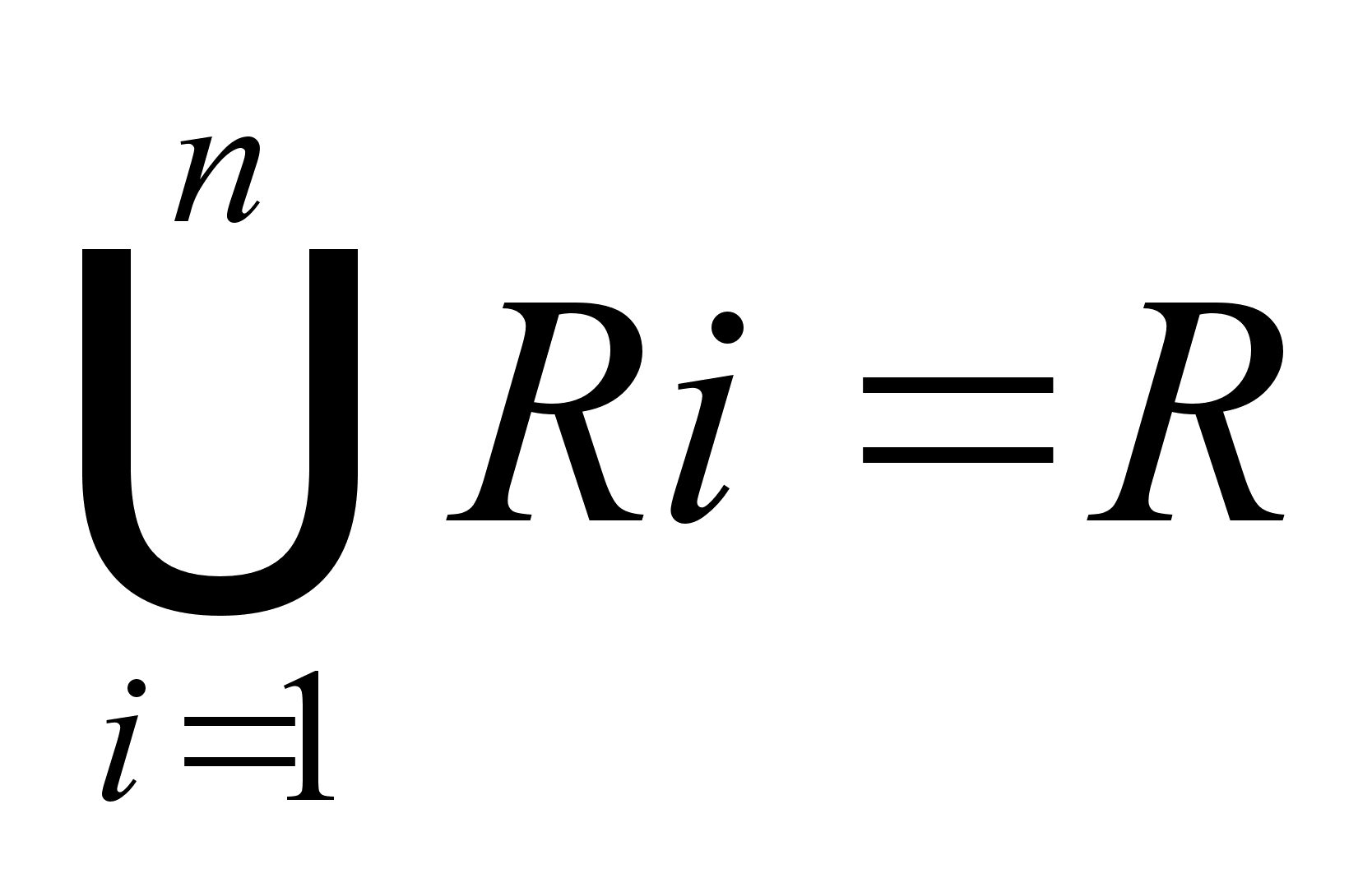
2. PiтАФсвязная область, i= 1, 2, .., п,

3. Ri Ri= для всех i и j, i 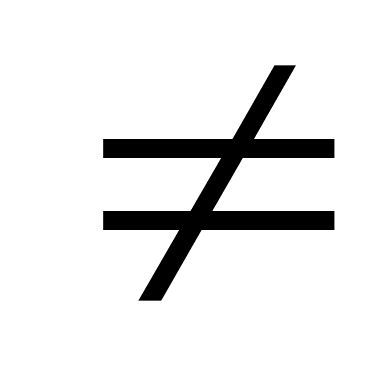j,

4. P(Ri) есть ИСТИНА для i= 1, 2, .., n;

5. P(Ri U Ri) есть ЛОЖЬ для i 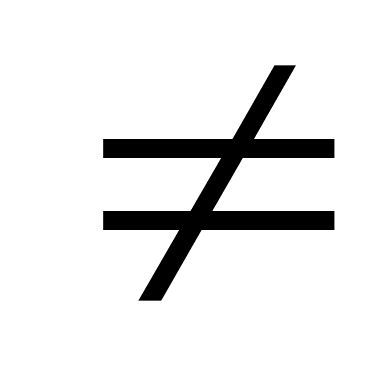j, где P(Ri)тАФ логический предикат, определенный на точках из множества Ri, и -пуВнстое множество.

Условие 1 означает, что сегментация должна быть полной, т. е. каждый пиксел должен находиться в образе. Второе услоВнвие требует, чтобы точки в области были связными. Условие 3 указывает на то, что области не должны пересекатьВнся. Условие 4 определяет свойства, которым должны удовлетвоВнрять пикселы в сегментированной области. Простой пример: Р(Ri) = ИСТИНА, если все пикселы в Ri имеют одинаковую интенсивность. Условие 5 означает, что области Ri и Ri разлиВнчаются по предикату Р.

2.3.2.Расширение области за счет объединения пикселов.

РасширеВнние области сводится к процедуре группирования пикселов или подобластей в большие объединения. Простейшей из них явВнляется агрегирование пикселов. Процесс начинается с выбора множества узловых точек, с которых происходит расширение области в результате присоединения к узловым точкам соседВнних пикселов с похожими характеристиками (интенсивность, текстура или цвет). Пусть цифры внутри ячеек указывают интенсивность. Пусть точки с координатами (3, 2) и (3, 4) используются как узловые. Выбор двух начальных точек приведет к сегментации образа на две области: области R1, свяВнзанной с узлом (3, 2), и области R2, связанной с узлом (3, 4). Свойство Р, которое мы будем использовать для того, чтобы отВннести пиксел к той или иной области, состоит в том, что модуль разности между интенсивностями пиксела и узловой точки не превышает пороговый уровень Т. Любой пиксел, удовлетворяюВнщий этому свойству одновременно для обоих узлов, произвольно попадает в область Ri. В этом случае сегментация проводится для двух областей, причем точки в R1 обозначаются буквой а, точки в R2 буквой . Необходимо отметить, что независимо от того, в какой из этих двух областей будет взята начальная точка, окончательный результат будет один и тот же. Если, с другой стоВнроны выбрать Т = 8, была бы получена единственная область

Предыдущий пример, неВнсмотря на его простоту, иллюстрирует некоторые важные проблемы расширения области. Двумя очевидными проблемаВнми являются: выбор начальных узлов для правильного представления областей, представляющих интерес, и опредеВнление подходящих свойств для включения точек в различные области в процессе расширеВнния. Выбор множества, состояВнщего из одной или нескольких начальных точек, следует из поВнстановки задачи. Например, в военных приложениях объекВнты, представляющие интерес, имеют более высокую темпераВнтуру, чем фон, и поэтому проВнявляются более ярко. Выбор наиболее ярких пикселов являВнется естественным начальным шагом в алгоритме процесса расширения области. При отВнсутствии априорной информаВнции можно начать с вычислеВнния для каждого пиксела наВнбора свойств, который наверВнняка будет использован при установлении соответствия пикВнсела той или иной области в процессе расширения. Если реВнзультатом вычислений являютВнся группы точек (кластеры), тогда в качестве узловых беВнрутся те пикселы, свойства коВнторых близки к свойствам центроидов этих групп. Так, в примере, приведенном выше, гистограмма интенсивностей показала бы, что точки с интенВнсивностью от одного до семи являются доминирующими. Выбор критерия подобия зависит не только от задачи, но также от вида имеющихся данных об образе. Например, анализ информации, полученной со спутников, существенно зависит от использования цвета. Задача анализа значительно усложнится при использовании только монохроматических образов. К сожаВнлению, в промышленном техническом зрении возможность полуВнчения мультиспектральных и других дополнительных данных об образе является скорее исключением, чем правилом. Обычно анализ области должен осуществляться с помощью набора десВнкрипторов, включающих интенсивность и пространственные хаВнрактеристики (моменты, текстуру) одного источника изображеВнния. Отметим, что применение только одних дескрипторов может приводить к неправильным результатам, если не используется информация об условиях связи в процессе расширения области. Это легко продемонстрировать при рассмотрении случайного расВнположения пикселов с тремя различными значениями интенсивВнности. Объединение пикселов в ВлобластьВ» на основе признака одинаковой интенсивности без учета условий связи приведет к бессмысленному результату при сегментаци.

Другой важной проблемой при расширении области является формулировка условия окончания процесса. Обычно процесс расширения области заканчивается, если больше не существует пикселов, удовлетворяющих критерию принадлежности к той или иной области. Выше упоминались такие критерии, как интенВнсивность, текстура и цвет, которые являются локальными по своей природе и не учитывают ВлисториюВ» процесса расширения области. Дополнительный критерий, повышающий мощность алгоритма расширения области, включает понятие размера, схоВнжести между пикселом-кандидатом и только что созданными пикселами (сравнение интенсивности кандидата и средней инВнтенсивности области), а также формы области, подлежащей расширению. Использование этих типов дескрипторов основано на предположении, что имеется неполная информация об ожиВндаемых результатах.

2.3.2.Разбиение и объединение области.

Изложенная выше проВнцедура расширения области начинает работу с заданного мноВнжества узловых точек. Однако можно сначала разбить образ на ряд произвольных непересекающихся областей и затем объВнединять и/или разбивать эти области с целью удовлетворения условий. Итеративные алгоритмы разбиения и объединения, работа которых направлеВнна на выполнение этих ограничений, могут быть изложены слеВндующим образом.

Пусть R является полной областью образа, на которой опреВнделен предикат Р. Один из способов сегментации R состоит в успешном разбиении площади образа на все меньшие квадратВнные области, так что для каждой области Ri, P(Ri) = ИСТИНА. Процедура начинает работу с рассмотрения всей области R. Если Р(R)= ЛОЖЬ, область разбивается на квадранты. Если для какого-либо квадранта Р принимает значение ЛОЖЬ, этот квадрант разбивается на подквадранты и т. д. Этот метод разбиения обычно представляется в виде так называемого квадродерева (дерева, у которого каждая вершина имеет только чеВнтыре потомка). Отметим, что корень дерева соответствует всему образу,а каждая вершина - разбиению. В данном случае только R4 подлежит дальнейшему разбиению. Если применять только опеВнрацию разбиения, можно ожидать, что в результате окончательВнного разбиения всей площади образа на подобласти последние будут иметь одинаковые свойства. Это можно устранить допуВнстимым объединением так же, как и разбиением. Для того чтобы удовлетворить условиям сегментации, введенным выше, необВнходимо объединять только те соседние области, пикселы которых удовлетворяют предикату Р, таким образом, две соседние облаВнсти Ri и Rk объединяются только в том случае, если P(Ri U Rk) = ИСТИНА.

Изложенное выше можно представить в виде процедуры, где на каждом шаге выполняются следующие операции:

1. Разбиение области Ri, для которой Р {Ri) = ЛОЖЬ, на четыре непересекающихся квадранта.

2. Объединение соседних областей Ri и Rk, для которых Р (Ri U Rk) = ИСТИНА.

3. Выход на останов, когда дальнейшее объединение или разбиение невозможно.

Возможны варианты этого алгоритма. Например, можно сначала разбить образ на квадратные блоки. Дальнейшее разбиение выполняется по изложенному выше способу, но вначале объединение ограничивается группами из четырех блоВнков, являющихся в квадродереве потомками и удовлетворяюВнщих предикату Р. Когда дальнейшее объединение этого типа становится невозможным, процедура завершается окончательным объединением областей согласно шагу 2. В этом случае объединяемые области могут иметь различный размер. ОсновВнным преимуществом этого подхода является использование одВнного квадродерева для разбиения и объединения до шага, на котором происходит окончательное объединение.


2.4. Применение движения

Движение представляет собой мощное средство, которое исВнпользуется человеком и животными для выделения интересуюВнщих их объектов из фона. В системах технического зрения роВнботов движение используется при выполнении различных операций на конвейере, при перемещении руки, оснащенной датВнчиком, более редко при перемещении всей робототехнической системы.

2.4.1.Основной подход.

Один из наиболее простых подходов для определения изменений между двумя кадрами изображения (образами) f(x, у, ti) и f(x, у, t,), взятыми соответственно в моменты времени ti и tj, основывается на сравнении соответВнствующих пикселов этих двух образов. Для этого применяется процедура, заключающаяся в формировании так называемой разности образов.

Предположим, что мы имеем эталонный образ, имеющий только стационарные компоненты. Если сравним этот образ с таким же образом, имеющим движущиеся объекты, то разность двух образов получается в результате вычеркивания стациоВннарных компонент (т. е. оставляются только ненулевые записи, которые соответствуют нестационарным компонентам изобраВнжения).

Разность между двумя кадрами изображения, взятыми в моВнменты времени ti и tj, можно определить следующим образом:


dij(x,y) = (*)


где тАФзначение порогового уровня. Отметим, что dij(x, у) приВннимает значение 1 для пространственных координат (х, у) только в том случае, если два образа в точке с этими координаВнтами существенно различаются по интенсивности, что опредеВнляется значением порогового уровня .

При анализе движущегося образа все пикселы изображений разности dij(x, у), имеющие значение 1, рассматриваются как результат движения объекта. Этот подход приметим только в том случае, если два образа зарегистрированы и освещенВнность имеет относительно постоянную величину в пределах границ, устанавливаемых пороговым уровнем . На практике записи в dij(x, у), имеющие значение 1, часто появляются в реВнзультате действия шума. Обычно на разности двух кадров изоВнбражения такие значения выглядят как изолированные точки. Для их устранения применяется простой подход, заключающийся в формировании 4- или 8-связных областей из единиц в dij(x, у), и затем пренебрегают любой областью с числом записей, меньВншим заранее заданного. При этом можно не распознать малые и/или медленно движущиеся объекты, но это увеличивает веВнроятность того, что остающиеся записи в разности двух кадров изображения действительно соответствуют движению.

2.4.2.Аккумулятивная разность.

Как говорилось выше, разность кадров благодаря шуму часто содержит изолированные записи. Несмотря на то что число таких записей может быть сокращено или полностью ликвидировано в результате анализа связности пороговых уровней, этот процесс может также привести к поВнтере изображений малых или медленно движущихся объектов. Ниже излагается подход для решения этой проблемы путем рассмотрения изменения в расположении пикселов на нескольВнких кадрах, т. е. в процесс вводится ВлпамятьВ». Основная идея заключается в пренебрежении теми изменениями, которые возВнникают случайно в последовательности кадров и, таким образом, могут быть отнесены к случайному шуму.

Рассмотрим последовательность кадров изображения f(x,y,t1), f(x, у, t2), .., f(x, у, tn) и допустим, что f(x, у, t1) является эталонным образом. Изображение аккумулятивной разности формируется в результате сравнения эталонного обВнраза с каждым образом в данной последовательности. В процедуре построения изображения аккумулятивной разности имеется счетчик, предназначенный для учета расположения пикВнселов. Его значение увеличивается каждый раз, когда возникает различие в расположении соответствующих пикселов эталонВнного образа и образа из рассматр

Вместе с этим смотрят:


11-этажный жилой дом с мансардой


14-этажный 84-квартирный жилой дом


16-этажный жилой дом с монолитным каркасом в г. Краснодаре


180-квартирный жилой дом в г. Тихорецке


2-этажный 3-секционный 18-квартирный жилой дом в г. Мирном