РЖсторiя математики Грецii

Реферат

з математики

на тему:

"РЖсторiя математики Грецii"

Протягом останнiх сторiч другого тисячорiччя до н.е. у басейнi Середземного моря й у прилягаючих до нього областях дуже багато чого змiнилося в економiцi i в полiтицi.

Бронзове столiття перемiнилося тим нашим столiттям, що ми називаiмо столiттям залiза, i вiдбувалося це в неясний час переселень i воiн. Лише деякi подробицi вiдомi нам про цю революцiйну епоху, але ми знаiмо, що до ii завершення, приблизно близько 900р. до н. е., уже не було царства Мiноса i Хетськоi держави, значно слабкiшими стали РДгипет i Вавiлон i на iсторичнiй сценi з'явилися новi народи. Найбiльш видатними серед них були iвреi, ассирiйцi, фiнiкiйцi i греки. Витиснення бронзи залiзом означало не тiльки переворот у вiйськовiй справi, але i прискорення росту економiки завдяки здешевленню засобiв виробництва, i це уможливило бiльш дiяльну участь широких шарiв суспiльства в справах економiчного i суспiльного значення.

Це позначилося у двох важливих нововведеннях:

замiнi незручного письма Стародавнього Сходу легко доступним алфавiтом;

веденнi карбованоi монети, що послужило пожвавленню торгiвлi.

Наступив той час, коли культурнi цiнностi вже не могли далi залишатися винятковим надбанням схiдного чиновництва.

Дiяльнiсть "морських розбiйникiв" - так iгипетськi тексти характеризують деякi народи, що переселялися - спочатку супроводжувалася чималими культурними втратами. Критська цивiлiзацiя зникла, iгипетське мистецтво занепало, наука Вавилону i РДгипту окостенiла на сторiччя. Немаi нiяких математичних текстiв цього перехiдного перiоду. Коли положення знову стало стiйким, Стародавнiй Схiд оправився, залишаючись в основному вiрним традицii, але було розчищено мiсце для цивiлiзацii цiлком нового складу - грецькоi цивiлiзацii.

Тi мiста, що виникли на узбережжя Малоi Азii й у самiй Грецii, уже не були адмiнiстративними центрами краiни зрошувального землеробства. Це були торговi мiста, де феодали-землевласники старого укладу були приреченi на поразку в боротьбi, що iм довелось вести з незалежним, отримавшими полiтичну самосвiдомiсть класом купцiв. Протягом сьомого i шостого сторiч до н. е. це купецтво узяло верх, але йому довелося у свою чергу вступити в боротьбу з дрiбними торговцями i ремiсниками, з демосом.

Пiдсумком був розквiт грецького полiса, самоврядноi мiста-держави - нове соцiальне явище, цiлком вiдмiнне вiд раннiх мiст-держав Шумеру й iнших краiн Сходу. Найбiльш значнi з цих мiст-держав, склалися в РЖонii, на анатолiйскому березi. РЗхня зростаюча торгiвля зв'язала iх iз всiм узбережжям Середземного моря, iз Двурiччям, РДгиптом, зi Скiфiiю i навiть бiльш далекими краiнами. Довгий час ведуче мiсце займав Мiлет. Але i мiста на iнших берегах: Коринф, пiзнiше Афiни у власне Грецii, Кротон i Гiарент в РЖталii, Сiракузи в Сицилii - ставали багатше i значнiше. Новий суспiльний уклад створив новий тип людини. Купець-мандрiвник нiколи ще не користався такою незалежнiстю, i вiн знав, що вона добута в завзятiй i жорстокiй боротьбi. Вiн нiяк не мiг роздiляти устоянi погляди Сходу. Вiн жив у перiод географiчних вiдкриттiв, порiвнянних тiльки з вiдкриттями захiдноiвропейського шiстнадцятого сторiччя, вiн не визнавав нi абсолютного монарха, нi влади, що з'являi у видi охоронного божества. А крiм того вiн мiг користатися вiдомим дозвiллям завдяки своiму багатству i працi рабiв. Вiн мiг помiзкувати про навколишнiй його свiт. Вiдсутнiсть цiлком сталоi релiгii привело багатьох мешканцiв цих прибережних мiст до мiстицизму, але це сприяло i протилежному - росту рацiоналiзму i науковому пiдходу.

Сучасна математика народилася в цiй атмосферi iонiйського рацiоналiзму - математика, що ставила не тiльки схiдне питання "як?", але i сучасне, наукове питання "чому?". Вiдповiдно до переказу батьком грецькоi математики i мiлетський купець Фалес, у першiй половинi шостого столiття Вавiлон i РДгипет, що вiдвiдав. Але якщо вiн навiть цiлком легендарна фiгура, то за нею коштуi щось цiлком реальне. Це - образ, що вiдповiдаi тим умовам, у яких закладалися основи не тiльки сучасноi математики, але i всiii сучасноi науки i фiлософii. Спочатку греки займалися математикою, маючи одну основну мету - зрозумiти, яке мiсце займаi у всесвiтi людина у рамках деякоi рацiональноi схеми. Математика допомогла знайти порядок у хаосi, зв'язати iдеi в логiчнi ланцюжки, знайти основнi принципи. Вона була найбiльш теоретичною з усiх наук.

Безсумнiвно, що грецькi купцi познайомилися зi схiдною математикою, прокладаючи своi торговi шляхи. Але люди Сходу майже не займалися теорiiю, i греки швидко знайшли це. Чому в рiвнобедрених трикутниках два кути рiвнi? Чому площа трикутника дорiвнюi половинi площi прямокутника при однакових пiдставах i висотах? Такi питання природно виникали в людей, що ставили подiбнi питання в областi космологii, бiологii i фiзики.

На жаль, у нас немаi першоджерел, що описують раннiй перiод розвитку грецькоi математики. Уцiлiлi рукописи вiдносяться до епохи християнства й iсламу i iх тiльки в малiй мiрi доповнюють замiтки в iгипетських папiрусах трохи бiльш раннього перiоду. Усе-таки класична фiлологiя дала можливiсть вiдновити тексти, що належать до четвертого сторiччя до н.е., i ми завдяки цьому маiмо у своiму розпорядженнi надiйнi видання Евклiда, Архiмеда, Аполлонiя й iнших великих математикiв античностi. Але в цих текстах перед нами вже цiлком розвита математична наука, i навiть за допомогою пiзнiших коментарiв по них важко простежити хiд iсторичного розвитку. Про епоху формування грецькоi математики приходиться судити, ТСрунтуючись лише на невеликих фрагментах, що приводяться в бiльш пiзнiх добутках, i на окремих зауваженнях фiлософiв i iнших не строго математичних авторiв. Дуже багато дотепностi i працi було вкладено в критику текстiв, завдяки чому удалося роз'яснити чимало темних мiсць у цьому ранньому перiодi. Ця робота, пророблена такими дослiдниками, як Поль Таннерi (Tannery), Хiт (Т.L. Heath), Цейтен (Н. G. Zeuten), Франк (Е. Frank) i iн., дозволяi нам дати у вiдомiй мерi зв'язну, хоча в значнiй частинi можливу картину грецькоi математики в епоху ii формування.

У шостому сторiччi до н.е. на руiнах Ассiрiйськоi iмперii виникла нова велика схiдна держава - Персiя Ахеменiдiв. Вона завоювала мiста Анатолii, але суспiльний лад грецькоi метрополii пустив уже глибокi коренi i його не можна було розтрощити. Перська навала була вiдбита в iсторичних битвах пiд Марафонi, Саламине i Платеi. Головним результатом грецькоi перемоги було розширення й експансiя Афiн. Тут у другiй половинi п'ятого сторiччя, при Перiклi, вплив демократичних елементiв увесь час зростало. Вони були рушiйною силою економiчноi i вiйськовоi експансii, i близько 430 р. вони зробили Афiни не тiльки центром Грецькоi iмперii, але i центром новоi i зацiкавленоi цивiлiзацii - золотого столiття Грецii.

В обстановцi суспiльноi i полiтичноi боротьби фiлософи i наставники викладали своi теорii i заодно нову математику. Вперше в iсторii група критично мислячих, "софiстiв", менш скована традицiiю, чим яка-небудь iнша попередня iй група вчених, стала розглядати проблеми математичного характеру скорiше з метою з'ясування iхньоi сутi, чим заради користi.

Тому що такий пiдхiд дозволив софiстам дiйти до основ точного мислення взагалi, було б надзвичайно повчально познайомитися з iхнiми мiркуваннями. До нещастя, вiд цього перiоду дiйшов лише один цiльний математичний фрагмент, що належить iонiйскому фiлософу Гiппократовi з Хiоса. Математичнi мiркування в цьому фрагментi на дуже високому рiвнi, i досить типово те, що в ньому розглядаiться зовсiм "непрактичний", але теоретично iстотне питання про так званих луночок - плоскi фiгури, обмежених двома круговими дугами.

Це питання - знайти площу таких луночок, у яких площа рацiонально виражаiться через дiаметр, - маi пряме вiдношення до центральноi проблеми грецькоi математики - квадратурi кола. Аналiз цiii проблеми в Гiппократа показуi, що в математикiв золотого столiття Грецii була упорядкована система плоскоi геометрii, у якiй у повному обсязi застосовувався принцип логiчного висновку вiд одного твердження до iншого ("апагоге"). Були закладенi основи аксiоматики, на що вказуi назва приписуваноi Гiппократовi книги "Початку" ("Stoicheia"), назва всiх грецьких аксiоматичних трактатiв, включаючи трактат Евклiда. Гiппократ дослiджував площi плоских фiгур, обмежених як прямими лiнiями, так i дугами окружностi. Вiн учить, що площi подiбних кругових сегментiв вiдносяться, як квадрати стягуючих iхнiх хорд. Вiн знаi теорему Пiфагора, а також вiдповiдна нерiвнiсть для непрямокутних трикутникiв. Весь його трактат уже мiг би бути вiднесений до евклiдовоi традицii, якби вiн не був старше Евклiда бiльш нiж на сторiччя.

Проблема квадратури кола - одна з "трьох знаменитих математичних проблем античностi", що у цей перiод стали предметом дослiдження.

Цi проблеми такi:

1) Трисекцiя кута, тобто подiл будь-якого заданого кута на три частини.

2) Подвоiння куба, тобто визначення ребра такого куба, що мав би обсяг, удвiчi бiльший обсягу заданого куба (так звана делiйська задача).

3) Квадратура кола, тобто перебування такого квадрата, площа якого дорiвнюi площi даного кругу.

Значення цих проблем у тiм, що iх не можна точно вирiшувати геометрично за допомогою кiнцевого числа побудов прямих лiнiй i окружностей - це можна зробити тiльки приблизно, - внаслiдок чого цi , проблеми стали засобом для проникнення в новi областi математики. У зв'язку з цими проблемами були вiдкритi конiчнi перетини, деякi кривi третього i четвертого порядку i трансцендентна крива, названа квадратриссою. Ми не повиннi з упередженням пiдходити до питанню про значення цих проблем через те, що iнший раз вони з'являлися у видi анекдоту (дельфiйськi пророцтва i т.п. ). Не раз траплялося, що основноi важливостi питання викладали у видi чи анекдоту головоломки - згадаiмо про яблуко Ньютона.

Математики рiзних епох, включаючи нашу, показали, який зв'язок iснуi мiж цими грецькими проблемами i сучасною теорiiю рiвнянь, зв'язок, що торкаiться питання про областi рацiональностi, алгебраiчнi числа i теорiю груп.

Ймовiрно, вiд групи софiстiв, що до деякоi мiри були зв'язанi з демократичним рухом, вiдмежувалася iнша група фiлософiв з математичними iнтересами, що примикав до аристократичних об'iднань. Вони називали себе пiфагорiйцями на честь засновника цiii школи Пiфагора, що, приблизно, був мiстиком, ученим i державним дiячем аристократичноi користi. Софiсти в бiльшостi пiдкреслювали реальнiсть змiн, пiфагорiйцi прагнули знайти в природi i суспiльствi незмiнне. У пошуках вiчних законiв свiту вони вивчали геометрiю, арифметику, астрономiю i музику. Найвидатнiшим iхнiм представником був Архiт з Тарента, що жив близько 400 р. до н.е. i школi якого, якщо ми приймемо гiпотезу Франка (Е. Frank), варто приписати велику частину "пiфагорiйськоi" математики. Арифметика пiфагорiйцiв була найвищою мiрою спекулятивною наукою i мала мало загального iз сучасноi iй обчислювальною технiкою Вавилона. Числа розбивалися на класи: парнi, непарнi, непарно-парнi, непарно-непарнi, простi i складенi, зробленi, дружнi, трикутнi, квадратнi, птАЩятикутнi i т, д. Деякi з найбiльш цiкавих результатiв отриманi для "трикутних чисел", що зв'язують арифметику i геометрiю:

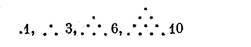
термiн тАЮквадратнi числатАЭ пiшов вiд побудов пiфагорiйцiв:

Самi фiгури значно старше, адже деякi з них ми знаходимо в неолiтичнiй керамiцi. Пiфагорiйцi ж дослiджували iхньоi властивостi, внесли сюди налiт свого числового мiстицизму i зробили числа основою своii фiлософii всесвiт, намагаючись звести всi спiввiдношення до числового ("усi i число"). Крапка була "помiщеною одиницею".

Пiфагорiйцям були вiдомi деякi властивостi правильних багатокутникiв i правильних багатогранникiв.

Вони показали, як заповнити площину системою правильних трикутникiв, чи квадратiв, чи правильних шестикутникiв, а простiр - системою кубiв. Згодом Арiстотель намагався доповнити це невiрним твердженням, що простiр можна заповнити правильними тетраедрами). Можливо, що пiфагорiйцi знали правильний октаедр i додекаедр - останню фiгуру тому, що кристали пiриту, що знаходяться в РЖталii, мають форму додекаедра, а зображення таких фiгур у орнаментах як магiчний символ вiдноситься ще до часiв етрускiв. Вони належать до кельтських племен Центральноi РДвропи початку епохи залiзного вiку ( 900 р. до н.е. ) i пiзнiше (пiрит був джерелом залiза).

Що стосуiться теореми Пiфагора, пiфагорiйцi приписували ii своiму наставнику i передавали, що вiн принiс у жертву богам сто бикiв на подяку. Ми вже бачили, що ця теорема була вiдома у Вавилонi часiв Хаммураппi, але дуже можливо, що перший загальний доказ був отриманий у школi пiфагорiйцiв.

Найбiльш важливим серед приписуваних пiфагорiйцям вiдкриттiв було вiдкриття iррацiонального у видi непорiвнянних вiдрiзкiв прямоi лiнii. Можливо, що воно було зроблено в зв'язку з дослiдженням геометричного середнього a:b = b:c, величиною, що цiкавила пiфагорiйцiв i служила символом аристократii. Чому дорiвнюi геометричне середнi одиницi i двiйки, двох священних символiв? Це вело до вивчення вiдносини сторiн i дiагоналi квадрата, i було виявлено, що таке вiдношення не виражаiться "числом", тобто тим, що ми тепер називаiмо рацiональним числом (цiлим чи числом дробом), а тiльки такi числа допускалися пiфагорiйською арифметикою.

Припустимо, що це вiдношення дорiвнюi р : q, де цiлi числа р и q ми завжди можемо вважати взаiмно простими. Тодi р2 = 2q отже, р2, а з ним i р - парне число, i нехай р = 2r. Тодi q повинно бути непарним, але, тому що q2 = 2r2, воно повинно бути також парним. Таке протирiччя дозволялося не розширенням поняття числа, як на чи Сходi в РДвропi епохи Вiдродження, а тим, що теорiя чисел для таких випадкiв вiдкидалася, синтез же шукали в геометрii.

Це вiдкриття, що порушило невимушену гармонiю арифметики i геометрii, iмовiрно, було зроблено в останнi десятилiття п'ятого сторiччя до н.е. Поверх того, виявилися iншi труднощi - виявилася в розумiннях про реальнiсть змiн, i цим фiлософи займаються до наших днiв. Вiдкриття цих нових труднощiв приписують Зеноновi Элейському (близько 450 р. до н.е. ), учню Парменiда, фiлософа-консерватора, що учив, що розум осягаi тiльки абсолютне буття i що змiна i тiльки удаване. Це придбало математичне значення тодi, коли в зв'язку з такими задачами, як визначення обсягу пiрамiди, сталi займатися нескiнченними процесами. Тут парадокси Зенона виявилися в протирiччi з деякими давнiми й iнтуiтивними представленнями вiдносно нескiнченно малого i нескiнченно великого. Завжди вважали, що суму нескiнченно багатьох величин можна зробити як завгодно великий, навiть якщо кожна величина вкрай мала, а також що сума кiнцевого чи нескiнченного числа величин розмiру нуль дорiвнюi нулю. Критика Зенона була спрямована проти таких представлень, i його чотири парадокси викликали таке хвилювання, що i зараз можна спостерiгати деякi брижi. Цi парадокси дiйшли до нас завдяки Аристотелю i вiдомi пiд назвами Ахiллес, Стрiла, Дихотомiя (розподiл на два) i Стадiони. Вони сформульованi так, щоб пiдкреслити протирiччя в поняттях руху i часу, але це зовсiм не спроба дозволити такi протирiччя.

Парадокси Ахiллес i Дихотомiя, що ми викладемо своiми словами, роз'яснять нам суть цих мiркувань.

Ахiллес. Ахiллес i черепаха рухаються в одному напрямку по прямiй. Ахiллес куди швидше черепахи, але, щоб ii нагнати, йому треба спочатку пройти точку Р, з якоi черепаха почала рух. Коли Ахiллес потрапить у Р, черепаха просунеться в точку Р1. Ахiллес не може наздогнати черепаху, поки не потрапить у P1 але черепаха при цьому просунеться в нову точку Р2. Якщо Ахiллес знаходиться в Р2, черепаха виявляiться в новiй точцi Р3 i т.д. Отже, Ахiллес нiколи не може наздогнати черепаху.

Дихотомiя. Допустимо, що я хочу пройти вiд А до В по прямiй. Щоб досягти В, менi треба спочатку пройти половину (АВ1) вiдстанi АВ; щоб досягти В2, я повинний спочатку досягти В2 на пiвдороги вiд А до В1 i так до нескiнченностi, так що рух нiколи не зможе початися.

Аргументи Зенона показали, що кiнцевий вiдрiзок можна розбити на нескiнченне число малих вiдрiзкiв, кожний з який - кiнцевоi довжини. Вони показали також, що ми натрапляiмо на труднощi при поясненнi того, який змiст заяви, що пряма "складаiться" iз крапок. Дуже iмовiрно, що сам Зенон не мав представлення про те, до яких математичних висновкiв приводять його мiркування. Проблеми, що привели до парадоксiв Зенона, незмiнно виникають у ходi фiлософських i теологiчних дискусiй. Ми в них бачимо проблеми, зв'язанi з вiдношенням, потенцiйноi й актуальноi нескiнченностi. Утiм, Поль Таннерi вважав, що мiркування Зенона насамперед були спрямованi проти пiфагорiйского представлення простору як суми крапок ("крапка i одиниця положення"). Як би справа нi обстояла, безсумнiвно, що мiркування Зенона впливали на математичну думку багатьох поколiнь. Його парадокси можна зiставити з млой, якими користався в 1734 р. iпископ Берклi, показуючи, до яких логiчних безглуздостей може привести погане формулювання положень математичного аналiзу, але не пропонуючи зi своii сторони кращого обТСрунтування.

Пiсля вiдкриття iррацiонального розумiння Зенона стали навiть ще бiльше турбувати математикiв. Чи можлива математика як точна наука? Таннерi думав, що ми можемо говорити про "дiйсний логiчний скандал" - про кризу грецькоi математики. Якщо справа обстояла саме так, то ця криза починаiться пiд кiнець Пелопонесськоi вiйни, що закiнчилася падiнням Афiн (404 р. до н, е.). Тодi ми можемо знайти зв'язок мiж кризою в математику i кризою суспiльноi системи, тому що падiння Афiн означало смертний вирок пануванню рабовласницькоi демократii i початок нового перiоду верховенства аристократii - криза, що була дозволена вже в дусi новоi епохи.

Для цього нового перiоду грецькоi iсторii характерно те, що росте багатство визначеноi частини правлячих класiв i так само ростуть убогiсть i незабезпеченiсть бiднякiв. Правлячi класи усе бiльше засобiв для iснування одержували за рахунок рабськоi працi. Це давало iм дозвiлля для занять мистецтвом i наукою, але заодно усе бiльш пiдсилювало iхню неприхильнiсть до фiзичноi працi. Цi дозвiльнi добродii з презирством вiдносилися до працi рабiв i ремiсникiв, i. заспокоiння вiд турбот вони шукали в заняттях фiлософiiю й етикою iндивiдуума. На таких позицiях коштували Платон i Аристотель. У "Республiцi" Платона (написаноi, iмовiрно, близько 360 р. до н.е. ) ми знаходимо саме чiтке вираження iдеалiв рабовласницькоi аристократii. "стражi" у республiцi Платона повиннi вивчати "квадривiум", що складаiться з арифметики, геометрii, астрономii i музики, для того щоб розумiти закони всесвiту.

Така iнтелектуальна атмосфера (принаймнi , у своiму ранньому перiодi) була сприятлива для обговорення основ математики i для умоглядноi космогонii. Частина сторiнки з першого видання "Початкiв" Евклiда, 1482 р.

Щонайменше три великих математики цього перiоду були зв'язанi з Академiiю Платона, а саме Архiт, Теiтет (розум. у 369 р.) i РДвдокс (ок.408-355). Теiтету приписують ту теорiю iррацiональних, котра викладена в десятiй книзi "Початкiв" Евклiда. РЖм'я Евдокса зв'язане з теорiiю вiдносин, що Евклiд даi у своiй п'ятiй книзi, а також з так званим методом вичерпування, що дозволив строго проводити обчислення площ i обсягiв. Це означаi, що саме РДвдокс переборов "кризу" у грецькiй математицi i що його строгi формулювання допомогли визначити напрямок розвитку грецькоi аксiоматики i, значною мiрою , усiii грецькоi математики.

Евдоксова теорiя вiдносин покiнчила з арифметичною теорiiю пiфагорiйцiв, застосовноi тiльки до сумiрних величин. Це була чисто геометрична теорiя, викладена в строгiй аксiоматичнiй формi, i вона зробила зайвими якi-небудь застереження щодо чи несумiрностi сумiрностi розглянутих величин.

Сучасна теорiя iррацiонального числа, побудована Дедекиндом i Вейерштрассом, майже буквально випливаi ходу думок Евдокса, але вона вiдкриваi значно бiльш широкi перспективи завдяки використанню сучасних математичних методiв.

"Метод вичерпування" (термiн "вичерпування" уперше з'являiться в Григорiя Сен Венсана, 1647 р.) був вiдповiддю школи Платона Зеноновi. Метод обходив усi пастки нескiнченно малого, попросту усуваючи iх, тому що зводив проблеми, у яких могли з'явитися нескiнченно малi, до проблем, розв'язуваним засобами формальноi логiки. Наприклад, якщо було потрiбно довести, що обсяг V тетраедра дорiвнюi однiii третини обсягу З призми з тiiю же пiдставою i тiiю же висотою, то доказ полягав у тому, щоб показати абсурднiсть як допущення, що V, так i допущення, що. 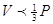Для цього була введена аксiома, вiдома тепер як аксiома Архiмеда. Вона лежить в основi теорii вiдносин Евдокса, а саме: "про тi величини говорять, що вони знаходяться в деякiм вiдношеннi одна до iншоi, котрi можуть, будучи помноженi, перевершити одна iншу" (Евклiд V, Визначення 4). Цей метод, що у грекiв в епоху Вiдродження став стандартним методом точного доказу при обчисленнi площ i обсягiв, був цiлком строгий, i його легко перетворити на доказ, що вiдповiдаi вимогам сучасноi математики.

Великим недолiком цього методу було те, що треба було заздалегiдь знати результат, щоб його довести, так що математик повинний був спершу прийти до результату менш строгим шляхом, за допомогою проб i спроб.

РД яснi вказiвки на те, що такого роду iнший метод дiйсно використовувався. Ми маiмо у своiму розпорядженнi лист Архiмеда Ератосфену (близько 250 р. до н.е. ), що було виявлено лише в 1906 р. i в який Архiмед описуi нестрогий, але плiдний спосiб одержання результатiв. Це лист вiдомий за назвою "Метод". С. Лур'i висунув припущення, що в ньому вираженi погляди математичноi школи, що суперничала зi школою Евдокса, виникла, як i та, у перiод кризи i зв'язана була з Демокрiтом, засновником атомiстики. Вiдповiдно до теорii Лур'i, школа Демокрита ввела поняття "геометричного атома". Передбачалося, що вiдрiзок прямоi, площа, обсяг складаються з великого, але кiнцевого числа неподiльних "атомiв". Обчислення обсягу тiла було пiдсумовуванням обсягiв усiх "атомiв", з яких складалося тiло. Ця теорiя може показатися безглуздою, якщо не згадати, що деякi математики епохи до Ньютона, особливо Вiiт i Кеплер, по сутi, користалися такими ж поняттями i вважали окружнiсть складеноi з дуже великого числа малюсiньких вiдрiзкiв. Немаi нiяких даних про те, що в стародавностi на такiй основi був розвитий строгий метод, але нашi сучаснi поняття межi дали можливiсть перетворити цю "атомну" теорiю в теорiю настiльки ж строгу, як i метод вичерпування. Навiть у нашi днi ми звичайно користуiмося таким поняттям "атома" при постановцi математичних задач у теорii пружностi, чи фiзику в хiмii, залишаючи строгу теорiю з переходами до межi професiйним математикам.

Перевага "атомного" методу перед методом вичерпування в тiм, що перший полегшуi перебування нових результатiв. Отже, в античностi був вибiр мiж строгим, але вiдносно марним методом i методом з хибким обТСрунтуванням, але бiльш плiдним. Повчально, що майже всi класичнi автори застосовують перший метод. Це знов-таки може бути зв'язане з тим, що математика стала коником дозвiльного класу, що спирався на рабство, байдужого до винаходiв, зi споглядальними iнтересами. Можливо i те, що в цьому позначилася перемога в областi фiлософii математики iдеалiзму Платона над матерiалiзмом Демокрiта.

У 334 р. до н.е. Олександр Македонський почав завоювання Персii. У 323 р., коли вiн помер у Вавилонi, всей Близьких Схiд був у руках грекiв. Полководцi Олександра роздiлили мiж собою його завоювання, i згодом виникли три iмперii: РДгипет, пiд владою Птолемеiв; Месопотамiя i Сирiя, пiд владою Селевкидiв; Македонiя, пiд владою Антигону i його спадкоiмцiв. Навiть у долинi РЖнду були грецькi князi. Почалася епоха еллiнiзму.

Прямим наслiдком походiв Олександра було те, що прискорилося проникнення грецькоi цивiлiзацii у великi райони схiдного свiту. Еллiнiзувались РДгипет, Месопотамiя, частина РЖндii. Греки заспiшили на Близький Схiд - торговцi, купцi, лiкарi, мандрiвники, найманцi, шукачi пригод. У мiстах - багато хто з них були недавно заснованi, що було легко розпiзнати по iхнiх еллiнiстичних назвах, - вiйськова справа й адмiнiстрацiя були в руках грекiв, населення було змiшаним, греко-схiдним. Але еллiнiзм був iстотно мiською цивiлiзацiiю. Село зберегло своi корiнне населення i свiй традицiйний життiвий уклад. У мiстах же стара культура Сходу стикалася з iмпортованою цивiлiзацiiю грекiв i частково змiшалася з нею, хоча завжди залишалося в силi глибоке розходження цих двох свiтiв. Монархи епохи еллiнiзму користувалися схiдним звичаям, вирiшували схiднi проблеми керування, але заохочували грецьке мистецтво, грецьку лiтературу i грецьку науку.

Так i грецька математика була пересаджена в нове середовище. Вона зберегла багато своiх колишнiх особливостей, але зазнала впливу вiд тих адмiнiстративних i астрономiчних запитiв, що висував Схiд. Таке тiсне зiткнення грецькоi науки зi Сходом виявилося винятково плiдним, особливо в першi сторiччя. Фактично вся дiйсно творча робота, що ми називаiмо "грецькою математикою", була пророблена за порiвняно короткий термiн вiд 350, до 200 р. до н.е. , вiд Евдокса до Аполлонiя, i навiть досягнення Евдокса вiдомi нам тiльки в тiм тлумаченнi, у якому ми iх знаходимо в Евклiда й Архiмеда. Чудово також, що найбiльшого розквiту ця еллiнiстична математика досягла в РДгиптi Птолемеiв, а не в Месопотамii, хоча у Вавiлонi корiнна математика була на бiльш високому рiвнi.

Можливо, що це було обумовлено центральним положенням РДгипту тiii епохи в средземноморському свiтi. Його нова столиця, Олександрiя, побудована на березi моря, стала розумовим i господарським центром еллiнiстичного свiту. Вавiлон же животiв, як вiддалений центр караванних шляхiв, та й зовсiм сходив зi сцени - його перемiнив Ктесифон-Селевкiя, нова столиця iмперii Селевкiдiв. Наскiльки вiдомо, жоден з великих грецьких математикiв не був коли-небудь, зв'язаний з Вавiлоном. В Антiохii i Пергаме, теж мiстах Селевкiдськоi iмперii, але бiльш близьких до Середземного моря, були важливi школи грецькоi науки. Однак корiнна вавiлонська астрономiя i математика саме при Селевкiдах досягли свого вищого рiвня, i ми тiльки тепер починаiмо краще розумiти, наскiльки iстотно був iхнiй вплив на грецьку астрономiю. Афiни стали освiтнiм центром, а Сiракузи дали Архiмеда, найбiльшого грецького Математика.

У цю епоху з'явилася професiйна вчений-людина, що присвячуi своi життя розвитку науки й одержуi за це винагороду. Деякi з найбiльш видатних представникiв такоi групи людей жили в Олександрii, де Птолемеi побудували великий науковий центр, так званий Музей з його знаменитою бiблiотекою. Там зберiгалася i множилася наукова i лiтературна спадщина грекiв i домоглися при цьому значних успiхiв. Одним з перших зв'язаних з Олександрiiю вчених був Евклiд, що i одним з найбiльш впливових математикiв усiх часiв.

Про життя Евклiда ми не маiмо нiяких достовiрних даних. Ймовiрно, вiн жив у часи першого Птолемея (306-283), якому, вiдповiдно до переказу, вiн заявив, що до геометрii нi "царськоi дороги". Його найбiльш знаменитий i найбiльш видатний здобуток - тринадцять книг його "Початки" (Stoicheia), але йому приписують кiлька iнших менших праць. Серед останнiх так званi "Данi" (Data), що мiстять те, що ми назвали б додатками алгебри до геометрii, але все це викладено строго геометричною мовою. Ми не знаiмо, яка частина цих праць належить самому Евклiду i якiй частинi складають компiляцii, але в багатьох мiсцях виявляiться разюча проникливiсть. Це першi, математичнi працi, що дiйшли до нас вiд древнiх грекiв цiлком. В iсторii Захiдного свiту "Початки", пiсля Бiблii, ймовiрно, найбiльше число раз видана i найбiльше вивчаiма книга. Пiсля винаходу друкарства з'явилося бiльше тисячi видань, а до того ця книга, переважно в рукописному видi, була основною при вивченнi геометрii. Велика частина нашоi шкiльноi геометрii запозичена часто буквально з перших шести книг "Початки", i традицiя Евклiда дотепер тяжii над нашим елементарним навчанням. Для професiйного математика цi книги усе ще мають непереборне зачарування, а iхня логiчна побудова вплинула на наукове мислення, мабуть, бiльше, анiж який би то не був iнший здобуток. Виклад Евклiда побудований у видi строго логiчних висновкiв теорем iз системи визначень, постулатiв i аксiом. У перших чотирьох книгах розглядаiться геометрiя на площинi. Виходячи з найбiльш простих властивостей лiнiй i кутiв, ми приходимо тут до рiвностi трикутникiв, рiвностi площ, теоремi Пiфагора, побудовi квадрата, рiвновеликого заданому прямокутнику, до золотого перетину, кола i до правильних багатокутникiв. У книзi V викладена РДвдоксова теорiя непорiвнянних у ii чисто геометричнiй формi, у книзi VРЖ ця теорiя застосована до подоби трикутникiв. Таке введення подоби - на настiльки пiзньому етапi - складаi одне з найбiльш iстотних розходжень мiж викладом планометрii в Евклiда i сучасним. Цi геометричнi розгляди завершуються в десятiй книзi, де багато хто вважаi найбiльш важкоi в Евклiда. У нiй дана геометрична класифiкацiя квадратичних iррацiональностей i коренiв квадратних з них, тобто тих чисел, що ми представляiмо у видi 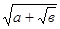. В останнiх трьох книгах викладаiться геометрiя в просторi. Вiд тiлесних кутiв, обсягiв паралелепiпедiв, призм i пiрамiд ми доходимо тут до кулi i до того, що за задумом повинне, видимо, вiнчати всю працю: дослiдження п'яти правильних ("Платонових") тiл i доказу, що iх iснуi тiльки п'ять.

Книги VРЖРЖ -РЖX присвяченi теорii чисел, але не технiцi обчислень, а таким "пiфагорейским" питанням, як подiльнiсть цiлих чисел, пiдсумовування геометричних прогресiй, i деяким властивостям простих чисел. Отут ми зустрiчаiмо i "алгоритм Евклiда" для визначення найбiльшого загального дiльника заданоi системи чисел, i "теорему Евклiда", що простих чисел нескiнченно багато. Особливий iнтерес представляi теорема VРЖ, у нiй мова йде про першу з задач, що дiйшли до нас, на максимум i доводиться, що з прямокутникiв заданого периметра найбiльшу площу маi квадрат. П'ятий постулат книги РЖ (неясно, у якiм вiдношеннi знаходяться в Евклiда "аксiоми" i "постулати") еквiвалентний так називанiй "аксiомi рiвнобiжних", вiдповiдно до якоi через крапку поза заданою прямою можна провести одну i тiльки одну пряму, iй рiвнобiжну. Спроби зробити з цiii аксiоми теорему змусили в дев'ятнадцятому сторiччi цiлком оцiнити мудрiсть Евклiда: це твердження було визнано аксiомою й у зв'язку з цим минулого вiдкритi iншi, так називанi неевклiдовоi геометрii.

Алгебраiчнi висновки в Евклiда приводяться винятково в геометричному видi. Вираження виду 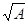вводиться як сторона квадрата з площею А, добуток а*в - це площа прямокутника зi сторонами а i в. Такий спосiб представлення насамперед був викликаний теорiiю вiдносин Евдокса, у якiй свiдомо вiдкидалися чисельнi вираження для вiдрiзкiв прямоi i, таким чином, непорiвняннi розглядалися тiльки геометрично: "числами" вважалися тiльки цiлi чи числа рацiональнi дроби.

Яку мету ставив собi Евклiд, коли писав своi "Початки"? Ми можемо з вiдомою впевненiстю думати, що вiн хотiв спiльно викласти в однiй працi три великих вiдкриття недавнього минулого: теорiю вiдносин Евдокса, теорiю iррацiональних Теiтета i теорiю п'яти правильних тiл, що займали видатне мiсце в космологii Платона. То були три типово "грецьких" досягнення.

Найбiльшим математиком епохи еллiнiзму й усього древнього свiту був Архiмед (287-212), що жив у Сiракузах, де вiн був радником Гiiрона. Вiн - один з деяких вчених античностi, яких ми знаiмо не тiльки по iменi: збереглися деякi зведення про його життя й особистiсть. Ми знаiмо, що вiн був убитий, коли римляни взяли Сiракузи, при облозi яких технiчне мистецтво Архiмеда було використано захисниками мiста. Подiбна схильнiсть до практичних застосувань представляiться нам дуже незвичайною, якщо врахувати, з яким презирством до цього вiдносилися сучасники Архiмеда зi школи Платона. Однак пояснення нам даi багато разiв цитоване повiдомлення Плутарха (у життiписi Марцеяла), а саме: "Хоча цi винаходи заслужили йому репутацiю надлюдськоi проникливостi, вiн не дойшов до того, щоб залишити який-небудь писаний твiр з таких питань, а, вважаючи низькою i невартою справою механiку i мистецтво будь-якого роду, якщо воно маi на метi користь i вигоду, усi своi честолюбнi домагання вiн засновував на власних поглядах", краса i тонкiсть яких не заплямованi якою-небудь домiшкою звичайних життiвих нестаткiв".

Найбiльш важливий внесок Архiмеда в математику вiдноситься до тiii областi, що тепер ми називаiмо iнтегральним численням: теореми про площi плоских фiгур i про обсяги тел. У "Вимiрi кола" вiн знайшов наближене вираження для окружностi, користаючись уписаними й описаними правильними багатокутниками. Дiйшовши в цьому наближеннi до багатокутникiв з 96 сторонами, вiн знайшов (у наших позначеннях), що

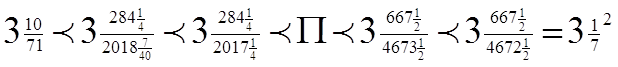
Звичайно про це повiдомляють, говорячи, що П приблизно дорiвнюi 3. У книзi Архiмеда "Про сферу i цилiндр" ми знаходимо вираження для поверхнi сфери (у такому видi: поверхня сфери в чотири рази бiльше площi великого кругу) i для обсягу сфери (у такому видi: обсяг сфери дорiвнюi обсягу описаного цилiндра).

У книзi про "Спiралi" ми знаходимо "спiраль Архiмеда" i обчислення площ, а в книзi "Про коноiди i сфероiди" - обсяги деяких тiл, утворених обертанням кривих другого порядку.

РЖм'я Архiмеда зв'язано також з його теоремою про утрату ваги тiлами, зануреними в рiдину. Ця теорема знаходиться в трактатi по гiдростатицi "Про тiла, що плавають,".

В усiх цих працях Архiмеда разюча оригiнальнiсть думки сполучаiться з майстерною технiкою обчислень i зi строгiстю доказiв. Характернi для цiii строгостi вже згадана "аксiома Архiмеда" i постiйне використання методу вичерпування при доказi його iнтеграцiйних результатiв. Ми бачили, що фактично вiн знаходив цi результати бiльш евристичним шляхом ("зважуючи" нескiнченно малi), але потiм вiн публiкував iх, дотримуючи самi твердi вимоги строгостi.

Достаток обчислень в Архiмеда вiдрiзняi його вiд бiльшостi творчих математикiв Грецii. Це додаi його працям, при всiх iхнiй типово грецьких особливостях, схiдний вiдтiнок. Такий вiдбиток помiтний у його "Задачi про бики" - дуже складнiй задачi невизначеного аналiзу, яку можна витлумачити як задачу, що приводить до рiвняння

t2 тАУ 4729494u2=1

типи "рiвняння Пелля", що зважуiться в дуже великих (цiлих) числах. Це лише одне з багатьох вказiвок на те, що традицii Платона нiколи безроздiльно не гocподарювали в математицi еллiнiзму, i на те ж саме вказуi еллiнiстична астрономiя.

9. З третiм великим математиком еллiнiзму, Аполлонiiм з Перги (260-170), ми знову цiлком у руслi геометричноi традицii грекiв. Аполлонiй, що, очевидно, вiв навчання в Олександрii й у Пергамi, написав трактат з восьми книг про конiчнi перетини ("Про конiкiв"). Сiм книг збереглося, три з них - тiльки в арабському перекладi. Це - трактат про елiпс, параболу i гiперболу, обумовлених як перетину кругового конуса, де виклад доведений до дослiдження эволют конiчного перетину. Ми називаiмо цi кривi, випливаючи Аполлонiю; цi назви виражають одне з властивостей цих кривих, зв'язане з площами i що виражаiться, у наших позначеннях, рiвняннями

у2 = рх, у2 = рх В±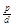 х2

"(запис однорiдна, в Аполлонiя р и d - вiдрiзки; знак " + " даi гiперболу, знак "-" даi елiпс). Парабола тут значить "додаток", елiпс - "додаток з недолiком", гiпербола - "додаток з надлишком". Аполлонiй не розташовував нашим координатним методом, тому що вiн не мав у своiму розпорядженнi алгебраiчнi позначення (ймовiрно, вiн свiдомо, пiд впливом школи РДвдокса, вiдкидав iх). Однак його результати можна вiдразу записати мовою координат, включаючи властивiсть, що збiгаiться з тим, що виражаiться iхнiм рiвнянням у декартових координатах. Те ж саме можна сказати про iншi книги Аполлонiя, що збереглися частково. Вони мiстять "алгебраiчну"

Вместе с этим смотрят:

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов