РЖнтегральнi характеристики векторних полiв
iнтегральнi характеристики векторних полiв
1. Диференцiальнi операцii другого порядку
Нехай в областi 
Вазаданi скалярне поле 
Ваi векторне поле 
, причому функцii 
Вамають в областi Ванеперервнi частиннi похiднi другого порядку. Тодi 
Ваi 
Ваi диференцiйовними векторними полями, а 
ВатАУ диференцiйовним скалярним полем.
До векторних полiв Ваi Ваможна застосувати операцii обчислення дивергенцii i ротора, а до скалярного поля 
ВатАУ операцiю обчислення градiiнта. Таким чином, отримуiмо повторнi операцii:
.
Операцiю 
Ваназивають оператором Лапласа i позначають також символом 
:
.
З допомогою оператора Гамiльтона оператор Лапласа записуiться у виглядi
.
Враховуючи, що
,
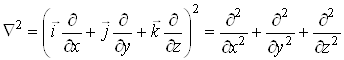дiстаiмо
.
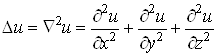Функцiя 
, яка задовольняi в деякiй областi рiвняння Лапласа 
, називаiться гармонiчною в цiй областi. Наприклад, лiнiйна функцiя 
Ваi гармонiчною в довiльнiй областi. Оператор Лапласа широко застосовуiться в рiвняннях математичноi фiзики. Вiдзначимо, зокрема, що потенцiал електричного поля точкового заряду або поля тяжiння точковоi маси, який маi вигляд 
, при 
Вазадовольняi рiвняння Лапласа:
(потенцiальне векторне поле 
Ваi безвихровим) i
(векторне поле 
Ваi соленоiдальним).
1. Двi iншi повторнi операцii 
Ваi 
ВаповтАЩязанi спiввiдношенням
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
де 
тАУ вектор-функцiя, координатами якоi i результати застосування оператора Лапласа до функцiй 
.
2. Розкладання векторного поля на суму потенцiального i соленоiдального полiв
Довiльне неперервно диференцiйовне векторне поле 
Ваможе бути зображено у виглядi
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
де 
ВатАУ потенцiальне поле, 
ВатАУ соленоiдальне поле.
Дiйсно, за означенням потенцiальне векторне поле Ваi градiiнтом деякого скалярного поля : 
. Тому для вектора Ваiз рiвностi (2) маiмо
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
Щоб векторне поле Вабуло соленоiдальним, воно маi задовольняти умову 
, звiдси, враховуючи рiвнiсть (3), знаходимо
.
Таким чином, для скалярного потенцiала поля Ваотримуiмо рiвняння
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
де 
ВатАУ вiдома функцiя даного поля .
Отже, якщо функцiя Ваi розвтАЩязком рiвняння (4), то, поклавши , , отримаiмо зображення поля Вау виглядi (2), де ВатАУ потенцiальне поле, ВатАУ соленоiдальне поле.
Рiвняння (2) тАУ неоднорiдне рiвняння в частинних похiдних другого порядку, яке називаiться рiвнянням Пуассона:
.
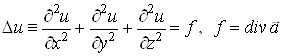Вiдзначимо, що це рiвняння маi (нескiнченну) множину розвтАЩязкiв, тому зображення поля Вау виглядi (2) не i iдиним.
2. Потiк векторного поля
Розглянемо векторне поле , визначене в просторовiй областi , i деяку кусково-гладку орiiнтовну поверхню 
. Нехай 
ВатАУ поле одиничних нормалей на обранiй сторонi поверхнi 
.
Як було вiдзначено в п. 4.2, поверхневий iнтеграл
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
називаiться потоком векторного поля Вачерез поверхню Вав сторону, яка визначаiться вектором 
Ва(кажуть також Влпотiк через обрану сторону поверхнi В»).
Якщо взяти iншу сторону поверхнi (змiнити орiiнтацiю), то вектор Вазмiнить напрям на протилежний; тому скалярний добуток 
, а отже, i потiк (поверхневий iнтеграл (5)) змiнить знак.
Якщо 
ВатАУ швидкiсть рухомоi рiдини, то 
Ваi кiлькiстю (обтАЩiмом) рiдини, яка протiкаi через поверхню Вау напрямi нормалi Ваза одиницю часу. Ця величина називаiться у фiзицi (гiдродинамiцi) потоком рiдини через поверхню . Тому i у випадку довiльного векторного поля Ваiнтеграл (5) називаiться потоком векторного поля через поверхню .
Розглянемо електричне поле 
Ваточкового заряду 
, який мiститься в точцi 
. Знайдемо потiк векторного поля Вачерез зовнiшню сторону сфери Варадiуса 
Ваз центром у точцi . Нехай 
Ва(
тАУ точка на сферi ); тодi 
. Тому
,
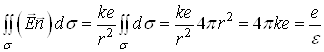де 
ВатАУ дiелектрична проникнiсть середовища, 
.
Якщо в системi координат 
, а 
, то вираз (5) для потоку векторного поля Ваможна записати у виглядi
.ВаВаВаВаВаВаВаВаВа (6)
Кожен доданок у правiй частинi рiвностi (6) залежить вiд вибору системи координат, проте iх сума, тобто потiк 
, очевидно, не залежить вiд вибору системи координат.
3. Формула Остроградського-Гаусса в векторнiй формi
Нехай в областi Вавизначено векторне поле ; ВатАУ замкнена поверхня, яка обмежуi область ; 
ВатАУ одиничний вектор зовнiшньоi нормалi до поверхнi Вау точцi .
Нехай, далi, 
Вата iхнi частиннi похiднi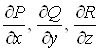 
Ванеперервнi в областi . Тодi справедлива формула Остроградського-Гаусса:
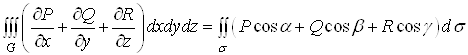.ВаВаВаВаВаВаВаВа (7)
Пiдiнтегральна функцiя в потрiйному iнтегралi i 
, а поверхневий iнтеграл тАУ потiк векторного поля 
Вачерез поверхню . Тому формулу (7) можна записати у векторнiй формi:
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)
Фiзичний змiст формули Остроградського-Гаусса: потiк векторного поля Вачерез замкнену поверхню в сторону зовнiшньоi нормалi дорiвнюi потрiйному iнтегралу по областi, обмеженiй цiiю поверхнею, вiд дивергенцii векторного поля . Щоб потiк був вiдмiнним вiд нуля, всерединi областi Вамають бути джерела (або стоки) поля. РЖз формули Остроградського-Гаусса випливаi, що тодi Ваi вiдмiнною вiд нуля. Таким чином, Вахарактеризуi джерела поля. Само векторне поле як би розходиться вiд джерел. Звiдси i походить назва ВлрозбiжнiстьВ» або ВлдивергенцiяВ».
4. Властивостi соленоiдального поля
Як вiдомо, векторне поле , яке задовольняi в областi Ваумову 
, називаiться соленоiдальним в цiй областi. Нехай область 
Ваi обтАЩiмно однозвтАЩязною. Це означаi, що, якщо кусково-гладка замкнена поверхня Валежить в областi , то i область, яка обмежуi поверхню , цiлком належить областi . Прикладами обтАЩiмно однозвтАЩязних областей i куля, паралелепiпед, тор. Вiдзначимо, що тор не i поверхнево однозвтАЩязною областю. Область, яка знаходиться мiж двома сферами, не i обтАЩiмно однозвтАЩязною (але i поверхнево однозвтАЩязною).
РЖз формули Остроградського-Гаусса випливаi, що соленоiдальне поле в взаiмно однозвтАЩязнiй областi маi таку властивiсть: потiк соленоiдального поля через довiльну замкнену поверхню, яка знаходиться в цiй областi, дорiвнюi нулю.
Вiдзначимо, що, якщо область не i обтАЩiмно однозвтАЩязною, то потiк соленоiдального (в цiй областi) поля через замкнену поверхню, яка знаходиться в областi, може бути вiдмiнним вiд нуля. Так електричне поле 
Ваточкового заряду, який мiститься в точцi , i соленоiдальним в кулi з викинутим центром (
при 
).
Слово ВлсоленоiдальнеВ» означаi ВлтрубастеВ». Для соленоiдального поля i справедливим закон збереження iнтенсивностi векторноi трубки. ЗтАЩясуiмо суть цього закону.
Нехай ВатАУ соленоiдальне поле. Розглянемо вiдрiзок Влвекторноi трубкиВ», тобто область, обмежену двома перерiзами 
Ваi 
Вата боковою поверхнею 
, яка складаiться iз векторних лiнiй (рис. 1). Застосуiмо до такоi областi формулу Остроградського-Гаусса (8). Оскiльки в соленоiдальному полi 
, то потiк векторного поля Вачерез поверхню областi дорiвнюi нулю: 
Ва( тАУ одиничний вектор зовнiшньоi нормалi). На боковiй поверхнi Вамаiмо 
, тому 
.
Отже,
.
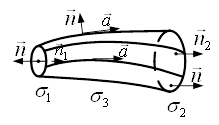
Рисунок 1 тАУ Вiдрiзок Влвекторноi трубкиВ»
Змiнимо на перерiзi Ванапрям нормалi Вана протилежний (
тАУ внутрiшня нормаль до ). Тодi отримаiмо
,
де обидва потоки через перерiзи Ваi Ваобчислюються в напрямi векторних лiнiй.
Таким чином, у соленоiдальному (трубчастому) векторному полi Вапотiк через будь-який перерiз векторноi трубки набуваi одного й того самого значення. Це i i закон збереження iнтенсивностi збереження векторноi трубки.
5. РЖнварiантне означення дивергенцii
Нехай в областi , обмеженiй поверхнею , визначено векторне поле . Запишемо формулу (8) для векторного поля Вав областi . Застосовуючи до лiвоi частини цiii формули теорему про середнi, отримаiмо
або
,
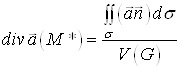де 
ВатАУ обтАЩiм областi , а 
ВатАУ деяка точка областi .
Зафiксуiмо точку 
Ваi стягуватимемо область Вадо точки Ватак, щоб Вазалишалася внутрiшньою точкою областi . Тодi 
, а Вапрямуватиме до . Внаслiдок неперервностi Вазначення 
Вапрямуватиме до . Таким чином, отримуiмо
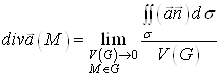.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
У праву частину формули (9) входять величини, iнварiантнi вiдносно вибору системи координат (потiк векторного поля через поверхню i обтАЩiм областi). Тому формула (9) даi iнварiантне означення дивергенцii векторного поля. Отже, дивергенцiя векторного поля залежить тiльки вiд самого поля i не залежить вiд вибору системи координат.
6. Циркуляцiя векторного поля
Розглянемо векторне поле , визначене в просторовiй областi , i деяку кусково-гладку криву 
, на якiй вказано напрям обходу (вибiр напряму обходу називають також орiiнтацiiю кривоi). Нехай 
ВатАУ одиничний дотичний вектор до кривоi 
Вау точцi , напрямлений в сторону обходу кривоi.
Криволiнiйний iнтеграл
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (10)
називаiться циркуляцiiю векторного поля Вавздовж кривоi Вау заданому напрямi.
Якщо взяти iнший напрям обходу кривоi (змiнити орiiнтацiю), то вектор 
Вазмiнить напрям на протилежний, тому скалярний добуток 
, а, отже, i циркуляцiя (криволiнiйний iнтеграл (10)) змiнить знак.
Якщо 
ВатАУ силове векторне поле, тобто 
ВатАУ вектор сили, то циркуляцiя 
Вавизначаi роботу силового векторного поля вздовж кривоi Вав заданому напрямi.
Якщо в прямокутнiй системi координат 
, а 
, то вираз (10) для циркуляцii векторного поля Ваможна записати в виглядi
.ВаВаВаВаВаВаВаВаВаВаВаВаВа (11)
Кожний доданок у правiй частинi (11) залежить вiд вибору системи координат, проте iхня сума, тобто циркуляцiя 
, очевидно, не залежить вiд вибору системи координат.
Якщо ввести вектор 
, то циркуляцiю можна записати у виглядi 
Ва(порiвняйте з правою частиною рiвностi (11)).
7. Формула Стокса у векторнiй формi
Нехай в областi Вавизначено векторне поле ; ВатАУ замкнений контур, який лежить в областi ; ВатАУ довiльна поверхня, межею якоi i контур ; 
Ва(Влповерхня Ванатягнута на контур В»); ВатАУ одиничний вектор нормалi на обранiй сторонi поверхнi .
Нехай функцii Вата iхнi частиннi похiднi першого порядку неперервнi на поверхнi . Тодi справедлива формула Стокса
,
де орiiнтацiя контуру Ваузгоджена з орiiнтацiiю поверхнi . Лiва частина формули Стокса i циркуляцiiю векторного поля Вавздовж контура , а права частина визначаi потiк через поверхню Вавекторного поля з координатами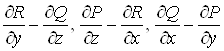 
, тобто потiк 
Вачерез поверхню . Тому формулу Стокса можна записати у векторнiй формi:
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (12)
або
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (13)
Фiзичний змiст формули Стокса: циркуляцiя векторного поля Вавздовж замкненого контуру дорiвнюi потоку ротора векторного поля Вачерез поверхню, натягнуту на цей контур.
8. Властивостi потенцiального поля
Як вiдомо, векторне поле , яке задовольняi в областi Ваумову 
, називаiться потенцiальним у цiй областi ( тАУ скалярний потенцiал поля ). Якщо поле Вапотенцiальне в областi , то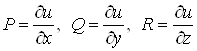 
Ваi вираз 
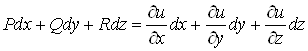Ваi повним диференцiалом функцii Вав областi . Це означаi, що виконана умова незалежностi криволiнiйного iнтеграла вiд шляху iнтегрування в просторi.
Таким чином, потенцiальне в областi Ваполе маi такi властивостi.
1. Циркуляцiя потенцiального поля Вавздовж довiльного замкненого контуру 
Вадорiвнюi нулю:
.
2. Для довiльних точок 
Ваi 
Ваобластi Вациркуляцiя потенцiального поля 
Вавздовж кривоi 
Ване залежить вiд вибору кривоi 
Ваi дорiвнюi рiзницi значень потенцiала Вав точках Ваi :
.
У випадку силового потенцiального поля ця властивiсть означаi, що робота такого поля вздовж кривоi Ване залежить вiд вибору кривоi, а залежить тiльки вiд початковоi i кiнцевоi точок Ваi .
3. Потенцiальне поле Ваi безвихровим, тобто 
.
Нехай тепер дано векторне поле , яке задовольняi в областi Ваумову 
. Чи випливаi звiдси, що поле Ваi потенцiальним в областi ? Вiдповiдь на це запитання залежить вiд форми областi . Якщо область Ваi поверхнево однозвтАЩязною, то iз умови 
Вавипливаi, що iснуi функцiя 
Ватака, що
.
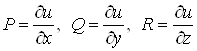Отже, 
, тобто поле Ваi потенцiальним в областi .
Таким чином, умова Ваi необхiдною i достатньою умовою потенцiальностi поля Вау поверхнево однозвтАЩязнiй областi.
Потенцiал Вапотенцiального поля Вау поверхнево однозвтАЩязнiй областi можна обчислити за формулою:
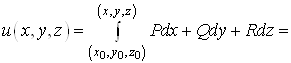
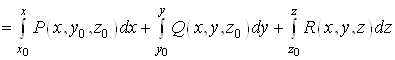.ВаВаВаВа ВаВаВаВаВаВаВаВа (14)
Якщо область Ване i поверхнево однозвтАЩязною, то умова Ване i достатньою для потенцiальностi поля Вав областi .
9. РЖнварiантне означення ротора
Нехай в областi Вавизначено векторне поле . Зафiксуiмо точку Ваi деяку площину, яка проходить через цю точку. Нехай ВатАУ одиничний вектор нормалi до площини, ВатАУ замкнений контур, який лежить в площинi i обмежуi область Ватаку, що ВатАУ внутрiшня точка областi . Запишемо формулу (12) для векторного поля Вав областi . Застосовуючи до правоi частини цiii формули теорему про середнi, отримуiмо
,
диференцiальне векторне поле формула соленоiдальне
звiдки
,
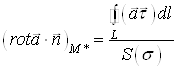де 
ВатАУ площа областi , ВатАУ деяка точка областi .
Стягуватимемо область Вадо точки Ватак, щоб Вазалишалася внутрiшньою точкою областi . Тодi 
, а Вапрямуватимемо до . Внаслiдок неперервностi Вазначення 
Вапрямуватимемо до 
. Таким чином, отримуiмо
.
У праву частину формули входять величини, iнварiантнi вiдносно вибору системи координат (циркуляцiя векторного поля вздовж замкненого контура i площа плоскоi областi). Тому дана формула даi iнварiантне означення проекцii Вав точцi Вана напрям, який виражаiться заданим вектором .
Отже, проекцiя ротора векторного поля на довiльний напрям, а отже, i сам Вазалежить тiльки вiд векторного поля Ваi не залежить вiд вибору системи координат.
Для означення вектора Вавищезазначеним способом достатньо розглянути в заданiй точцi Вапроекцii Вана три довiльних некомпланарних напрями. Такими трьома проекцiями Вавизначаiться однозначно.
Размещено на http://" onclick="return false">
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы