Математичний бiльярд

Вступ

Обрана мною тема курсовоi роботи тАУ математичнi бiльярди тАУ i дуже цiкавою i актуальною. В умовах розвитку комптАЩютерних технологiй, створень математичних пакетiв для вирiшення багатьох задач з рiзних галузей математики постаi проблема пошуку найбiльш оптимальних шляхiв розвтАЩязання. Не останню роль в вирiшеннi цiii проблеми граi вивчення теорii математичних бiльярдiв. Тому розгляд цього питання, встановлення звтАЩязкiв основ цiii теорii з рiшеннями проблем iнформатики, фiзики i достатньо важливим компонентом навчального курсу ВлВища математикаВ». Крiм цього, деякi вiдомостi доречно було б вивчати в середнiй школi для розвтАЩязання задач пiдвищеноi складностi, при пiдготовцi учнiв до математичних олiмпiад, на факультативах з математики та в класах з поглибленим вивченням математики.

Вивчення математичних бiльярдiв, як системи руху абсолютно пружного тiла (без врахування опору середовища), послужило основою концепцii детермiнованого хаосу. До систем, вiдповiдаючiм бiльярдам, зводяться ряд задач статистичноi фiзики. Багато складних для аналiтичного розвтАЩязання математичних задач легко розвтАЩязуються за допомогою побудови траiкторiй бiльярдiв в прямокутнiй та опуклiй областi. Чiтко простежуiться звтАЩязок такоi науки, як оптики з проблемами побудови траiкторiй математичних бiльярдiв в елiпсi та iн.

Все це свiдчить про необхiднiсть подальшого розгляду цiii теми, використання для вирiшення питань теорii бiльярдiв сучасних комптАЩютерних програм. Тому метою моii роботи було вивчення основних теоретичних вiдомостей вищезазначеноi теми, аналiз можливостей застосування законiв теорii в середнiх навчальних закладах та використання комптАЩютерних програм для оптимiзацii роботи з пошуку рiшення проблемних питань, для наочноi демонстрацii правил побудови бiльярдних траiкторiй та розширення сфери застосування теорii математичних бiльярдiв. Для цього були вивченi роботи вiдомих математикiв, що займались цiiю проблемою, проведена спiльна з викладачами вищоi математики та iнформатики ХНПУ iм. Г.С. Сковороди дослiдницька робота. В результатi проведеноi роботи були отриманi наступнi висновки, що представленi в двох роздiлах даноi курсовоi роботи.

Вiдомостi з теорii математичних бiльярдiв

ОбтАЩiкт та iсторiя вивчення теорii

Назва бiльярд походить вiд французького ВлbilliardВ» - крива палка або ВлbillartВ» (кий) та ВлbilleВ» (куля).

Подiбно до того, як азартна гра у костi викликала до життя ВлобчисленняВ» вiрогiдностi, гра в бiльярд стала предметом серйозних наукових дослiджень з механiки та математики. Опису руху бiльярдноi кулi присвячена книга видатного французького фiзика Г.Г. Корiолiса, створена ним в 1835 роцi. Окремi вiдомостi цiii працi будуть наведенi в подальших роздiлах даноi курсовоi роботи.

Вiдомi рiзнi варiанти гри на бiльярдi. Наприклад, так званий французькiй бiльярд взагалi не маi луз. При грi в цей бiльярд треба попасти в задану кулю пiсля декiлькох зiткнень з iншими кулями. Французький бiльярд i став прообразом математичного бiльярда.

ОбтАЩiктом вивчення в математичних бiльярдах i траiкторiя, тобто слiд рухомоi бiльярдноi одиницi. В загальному випадку ця ламана, що вписана в область Q i складена з нескiнченноi кiлькостi ланок, на яких вказано напрям руху. Ця ламана може бути однозначно побудована по будь-якiй своiй ланцi. В окремому випадку, коли бiльярдна частка вертаiться в вихiдне положення (i пiсля цього знов розпочинаi свiй рух), ламана замкнена i складаiться з скiнченоi кiлькостi ланок. Така траiкторiя називаiться перiодичною. Основна цiль теорii математичних бiльярдiв тАУ опис всiляких типiв траiкторiй в рiзних областях.

Бiльярди призводять до багатьох цiкавих i красивих математичних задач. О декiлькох з них розповiдаiться в другiй частинi даноi роботи.

Цi задачi бувають далеко не простими i приховують в собi багато невирiшених проблем. Наприклад, досi невiдомо, чи в будь-якiй областi iснуi перiодична бiльярдна траiкторiя (це невiдомо навiть для многокутникiв). РЖще один приклад пов'язаний з проблемою висвiтлення довiльноi областi з дзеркальними стiнками точковим джерелом свiтла: з деякоi точки q тВм Q випустимо рiзноманiтнi променi свiтла, що дзеркально вiдбиваються вiд границi ∂Q; чи освiтлять вони (пiсля можливих вiдбиттiв) всю область Q? Вiдповiдь невiдома, якщо Q тАУ многокутник. Для плоских областей загального вигляду вiдповiдь негативна.

Окрiм використання в чисто математичних задачах, бiльярди цiкавi тим, що моделюють досi складнi фiзичнi процеси. Традицiйно бiльярди використовуються в оптицi (дзеркальне вiдбиття, задачi про освiтлення, фокусiровка променiв в лазерi) та акустицi (побудова Влшепочущiх галерейВ»), оскiльки променям свiтла та звуковими хвилям притаманнi пружнi (дзеркальнi) вiдбиття вiд непроникних поверхонь.

До бiльярдiв можуть бути зведенi деякi важливi моделi класичноi механiки i гiдродинамiки тАУ гази i рiдини, що складенi з молекул, пружно стикаються один з одним та з стiнками iмкостi (системи твердих куль). Тут закон пружного зiткнення покладено в самiй моделi, зостаiться лише уявити (закодувати) рух багатьох молекул траiкторiiю однiii бiльярдноi частки. Багато проблем класичноi механiки твердих куль можуть бути сформульованi i вирiшенi в термiнах бiльярдiв. Наприклад, так було розвтАЩязане питання про можливу кiлькiсть зiткнень в системi з нескiнченноi кiлькостi твердих куль у вiдкритому просторi (без стiнок).

Бiльярднi траiкторii виникають при знаходженнi власних функцiй оператора Лапласа всерединi випуклоi областi з граничними умовами.

Нескiнченно можна перераховувати можливостi застосування теорii математичних бiльярдiв. Останнiм часом статистична механiка дала великого iмпульсу розвитку теорii бiльярдiв. Тому надалi придiлимо iй найбiльшу увагу.

Проблема чiткого обТСрунтування законiв статистичноi механiки здавна хвилювала розум вчених (в повному обсязi вона не вирiшена й досi). Мова йде про вивiд законiв еволюцii систем великоi кiлькостi часток (компонент) з рiвнянь руху кожноi окремоi частки (компоненти) пiд впливом всiх iнших часток. Ще в позаминулому сторiччi Л. Больцман вказав, що визначенi математичнi властивостi системи твердих куль можуть бути корисними для такого висновку. Властивостi цi тАУ ергодичнiсть, перемiшування та iншi тАУ не такi простi. Цi властивостi (iх називають стохастичним) виявляються також корисними при вивченнi багатьох iнших явищ, наприклад квантового хаосу.

Ергодичнi властивостi бiльярдiв обговорювалися ще в працях А. Пуанкаре, Г. Бiркгофа i Ж. Адамара. Великий внесок в розумiння ролi цих властивостей для проблем статистичноi механiки внiс радянський фiзик Н. С. Крилов. Математичний апарат для вивчення ергодичних властивостей бiльярдiв зтАЩявилися в 70-х роках, пiсля того, як в серii праць Д.В. Аносова, Я.Г. Сiная, С. Смейла та iнших було створено новий напрямок теорii динамiчних систем, що отримало назву теорii гiперболiчних динамiчних систем. Перше фундаментальне дослiдження ергодичних властивостей бiльярдiв належить Я.Г. Сiнаю. Його праця вiдкрила дверi для проникнення динамiчних систем (хаосу, безповоротностi руху, дифузii, релаксацii, рiвноваги) в математичну теорiю бiльярдiв.

В умовах сучасностi теорiя бiльярдiв здобула вiдомiсть i отримала широке визнання в науковому свiтi. Стали звичними такi поняття, як Влстохастичний бiльярдВ», Влквантовий бiльярдВ» Влентропiя бiльярдуВ», Влстатистичнi властивостi бiльярдуВ». В той же час, це порiвняно молода теорiя. Тому можливостi використання новiтнiх технологiй розвтАЩязання можливо допоможуть знайти вiдповiдь на ще нерозвтАЩязанi задачi даноi теорii.

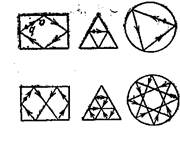
Перейдемо до загальноi математичноi проблеми бiльярду. Вона полягаi в тому, щоб змалювати рiзноманiтнi типи бiльярдних траiкторiй в данiй областi Q. Найпростiший принцип такого змалювання тАУ роздiл траiкторiй на перiодичнi, або замкненi, i iншi тАУ неперiодичнi. На малюнку зображенi деякi перiодичнi траiкторiй бiльярдiв в прямокутнику, в правильному трикутнику, в колi.

Траiкторiя з Влпочатковою умовоюВ» (напрямок, початкове положення точки) буде перiодичною, якщо через деякий час (через перiод) точка повертаiться в своi першочергове положення з первинною швидкiстю. Перiодичний рух сприймаiться як найбiльш ВлправильнийВ». Проблема перiодичних траiкторiй зводиться до iснування: чи в будь-якiй областi iснують замкненi траiкторii?

РЖще одне питання тАУ про критерii перiодичностi: як по даним умовам визначити, чи i задана теорiя перiодичною?

Цiкавiсть представляють такi питання:

ü Яку кiлькiсть ланок може мати перiодична траiкторiя?

ü Якi перiоди мають перiодичнi траiкторii в данiй областi? (цi питання мають пряме вiдношення до дослiдження спецiальних систем квантовоi механiки). Перейдемо до розглядання цих питань в простiших поверхневих областях (коло, елiпс, прямокутник, трикутники).

Бiльярди в опуклих гладких областях

Бiльярд в колi

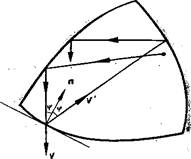
Бiльярд в крузi. Найпростiша область з криволiнiйною гладкою межею на площинi тАФ це, звичайно ж, круг. Правильна, симетрична форма круга приводить до правильного руху бiльярдноi частки: при вiддзеркаленнях вiд межi круга кут падiння залишаiться постiйним!

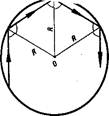
Мал. 1

Якщо цей кут ще i рацiональний (в градусах, наприклад, 45В°, 30В°, 1В° або 2,5В°), то точки вiддзеркалення лягають у вершини правильного многокутника i рух бiльярдноi частки буде перiодичним (тобто вона рано чи пiзно повернеться в первинне положення i в точностi вiдтворюватиме свою траiкторiю) . Якщо ж кут падiння iррацiональний, то точки вiддзеркалення усюди щiльно заповнюватимуть коло (тобто на будь-якiй маленькiй дузi iх буде нескiнченно багато) i траiкторiя нiколи не повернеться в початкове положення. Цей цiкавий i досить елементарний факт витiкаi з теореми Якобi.

Для нас важливо, що у всiх випадках i величина, яка зберiгаiться при русi частки. Ця величина тАФ кут падiння. Така величина називаiться iнварiантом, а у фiзицi тАФ частiше першим iнтегралом.

В· Рiвнiсть всiх траiкторiй (з рiвностi кутiв)

В· Середини всiх ланок траiкторii вiддаленi вiд центра кола на однакову вiдстань.

Будь-яка бiльярдна траiкторiя в колi нiколи не заходить всередину деякого концентричного кола, границi якого дотикаються всi ii ланки, тобто це значить, що бiльярд в колi не ергодичний.

Бiльярдна траiкторiя в колi не всюди щiльна. Вид бiльярдноi траiкторii в колi повнiстю визначаiться числом α, а саме

Якщо число α таке, що α/π i рацiональним числом (тобто дорiвнюi деякому дробу m/n з цiлими m i n), то бiльярдна траiкторiя перiодична

Якщо α/π iррацiональне, то вiдповiдаюча куту α траiкторiя неперiодична.

Доведення

Α =m/n*2π , m,n тАУ цiлi

Nα = 2πm, при поворотi на кут nα кожна точка Г переходить в себе.

P₀P₁P₂P₃ (вершини бiльярдноi траiкторii: P_n=P₀; P_n+1 = P₁ ; P_n+2 = P_2тАж)

Тобто вершини, починаючи з n-оi повторюються. (що i свiдчить про перiодичнiсть бiльярдних траiкторiй)

Якщо m/n нескоро чувана, то траiкторiя складаiться з n ланок. При m=1 тАУ це буде правильний n-кутник, при m>=2 траiкторiя представляi собою правильну самоперетинаючуюся замкнену (зiрчасту) ламану! Бiльярдний шар пiсля n вiддзеркалень вiд борта Г опиняiться в початковiй точцi P₀ (зробив m обертiв навколо центру О).

Уявiмо, що бiльярдна траiкторiя перiодична/, тодi α i π такi, що α/π тАУ рацiональнi, а це протирiчить умовi, що α/πтАУ iррацiональне. Теорему доведено.

Теорема Якобi. Нехай α тАУ невимiрне з π (α/π - iррацiональне), {P_0,P_1,P_2,тАж}={ P_k} тАУ нескiнченна послiдовнiсть точок послiдовностi P_k+1 отримуiться з попередньоi точки P_kповоротом навколо центра на α радiан. Тодi для будь-якоi дуги Δ кола Г хоча б одна точка послiдовностi { P_k} лежить на цiй дузi.

Теорема Якобi стверджуi, що якщо коло провертати на iррацiональний (в градусах) кут р, то образи кожноi точка а, а+р, а+2р .. (в кутових координатах, узятих по модулю 360В°) заповнять щiльно все коло.

Неперiодичний рух може виявитись Влмайже перiодичнимВ», або квазiперiодичним. Квазiперiодичнiсть означаi, що хоч його траiкторiя i не замкнена, але через деякий час (через квазiперiод) вона буде близько до попереднього вiдрiзку траiкторii. Характернi квазiперiодичнi траiкторii для кола показано на малюнку.

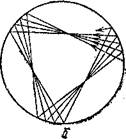
Виявляiться, для бiльярда в колi неперiодична траiкторiя маi бути квазiперiодичною. Вказанi неперiодичнi траiкторii всюди щiльно заповнюють вiдповiдну область. Якщо вважати, що бiльярдний шар ВлчорнильнийВ» i залишаi пiсля себе слiд, то вiн з часом обовтАЩязково замалюi всю область цiлком. Зрозумiло, що перiодична траiкторiя властивостi всюди щiльноi мати не може тАУ вона може заповнювати область Влдуже щiльноВ», але не всюди щiльно. Довiльна неперiодична траiкторiя бiльярда в колi та елiпсi не i всюди щiльною.

Бiльярд в кiльцi. Ще одним прикладом досить правильноi областi з гладкою криволiнiйною межою служить кiльце, тобто область, укладена мiж двома концентричними колами. В кiльцi бувають траiкторii двох типiв:

а) що вiдображаються тiльки вiд зовнiшнього круга тАФ цi траiкторii зберiгають кут падiння, як i в крузi (вони не ВлвiдчуваютьВ» присутностi внутрiшнього круга);

б) що вiдображаються поперемiнно вiд зовнiшнього i вiд внутрiшнього кругiв.

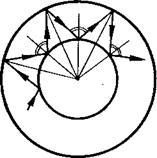Траiкторii типу ВлбВ» трохи складнiше, нiж типу ВлаВ», але i у них кути падiння на зовнiшнi коло однаковi. РЖ на внутрiшню тАФ теж, що видно з мал.

Траiкторii математичного бiльярду в елiпсi

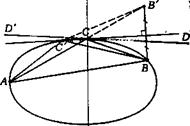
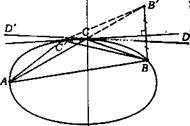
Природним узагальненням круга в математицi i елiпс. Цiкава властивiсть бiльярдiв в елiпсi: як би ми не випустили бiльярдний шар з одного фокусу, вiн пiсля одного вiддзеркалення вiд елiпсу пройде через другий фокус, пiсля другого тАУ через перший фокус. (дотична до елiпса, що проведена в його довiльнiй точцi М, утворюi рiвнi кути з вiдрiзком F₁M F₂M, що зтАЩiднують обидва фокуси з цiiю точкою).

Теорема про каустик в елiпсi. Якщо одна ланка бiльярдноi траiкторii в елiпсi Э₀ проходить через фокус, то i вся решта ланок проходить через фокуси. Якщо ж жодна ланка траiкторii не проходить через фокуси, то всi ii ланки торкаються однiii i тiii ж кривоi. Цiiю кривою i або елiпс Э₁ софокусний з даним, або гiпербола Г₁, софокусна з даним елiпсом Э₀ (в останньому випадку торкатися гiперболи Г₁ можуть не самi ланки, а iх продовження за точку вiддзеркалення).

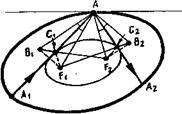
Кривi, якi одночасно торкаються всiх ланок бiльярдноi траiкторii, називаються ii каустиком. Точнiше, каустика в бiльярдi тАФ це така крива, що якщо бiльярдну частку запустити по дотичнiй до неi, то пiсля вiддзеркалення частка також полетить по дотичнiй до цiii ж кривоi. Термiн ВлкаустикуВ» запозичений з оптики, де вiн означаi лiнiю, огинаючу свiтловий пучок в мiсцi його сходження пiсля вiддзеркалення вiд дзеркала (назва ВлкаустикаВ» означаi ту, що ВлпекучаВ», оскiльки каустик служить мiсцем концентрацii енергii).

Доказ теореми:

(тiльки для каустик-елiпсiв) Тут F₁ i F₂ тАФфокуси елiпса, а А₁АА₂ - двi ланки бiльярдноi траiкторii. Точка В₁ i В₂ симетричнi фокусам F₁ i F₂ вiдносно прямих А₁А i А₂А. Добре вiдомо, що вiдрiзки F₁А i F₂А утворюють однаковi кути з дотичною до елiпса в точцi А. Тому всi чотири кути тА№В₁АА₁, тА№А₁АF₁ тА№F₂AA₂ i тА№A₂AB₂ рiвнi мiж собою. Отже, трикутники АВ₁F₂ i AB₂F₁ рiвнi, тобто B₁F₂=B₂F₁. Звiдсiля |F₁C₁| + |F₂C₁| = |F₁C₂| + |F₂C₂|, де С₁ i С₂ тАУ точки перетину АА₁ з В₁F₂ i AA₂ з B₂F₁.Значить, С₁ i С₂ лежать на одному елiпсi з фокусами F₁ i F₂, для якого вiдрiзки АА₁ i АА₂ i дотичними. До речi, каустики i i у бiльярда в колi тАУ це концентричнi кола меншого радiусу.

Математичний бiльярд на прямокутному столi без луз

Бiльярдом в прямокутнику називаiться така система: один точковий бiльярдний шар на прямокутному бiльярдному столi ABCD без луз, що рухаiться по ньому без тертя i вiддзеркалюiться вiд його сторiн (ВлбортiвВ») по бiльярдному закону Влкут падiння дорiвнюi куту вiддзеркаленняВ».

Найпростiшi бiльярднi траiкторii в прямокутнику тАУ перiодичнi. Вони можуть бути декiлькох типiв: складатися з дворазово пройдених вiдрiзкiв мiж протилежними сторонами (малюнок а)); утворювати родини паралелограмiв зi сторонами, паралельними дiагоналям прямокутника (малюнок б)); утворювати замкненi ламанi (малюнок в))

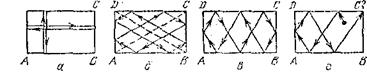
Бувають i такi траiкторii, якi попадають в вершини прямокутника. В такому випадку незрозумiло, як шару належить рухатися пiсля виходу Влз кутаВ». Такi траiкторii мають назву тАУ особi, i якщо траiкторiя попадаi в вершину, обривають ii, i вiд траiкторii залишаiться тiльки ii частина (напiвтраiкторiя). Але у випадку прямокутного бiльярду шар можна вважати вилетiвшим пiсля попадання в вершину в точностi у протилежному напрямку. (Такого висновку не можна робити для бiльярду в довiльному многокутнику.)

Намалювати хоча б одну неперiодичну траiкторiю бiльярда в прямокутнику вже значно важче. Задача про розпiзнання перiодичних i неперiодичних траiкторiй бiльярда розвтАЩязуiться за допомогою процедури Влвипрямлення траiкторiйВ»

Випрямлення траiкторii в довiльному многокутнику

Нехай Р₁Р₂Р₃тАж - довiльна не особлива траiкторiя бiльярда в многокутнику Q=А₁А₂А₃.А_n. Побудуiмо по цiй ламанiй спецiальну пряму. А саме, вiдобразимо наш многокутник Q разом з ламаною Р₂Р₃Р₄тАж вiдносно тiii сторони многокутника, на якiй лежить точка Р₂ (першу ланку ламаноi Р₁Р₂ ми не чiпаiмо). Згiдно закону вiддзеркалення, вiдрiзок Р₂Р₃ симетричний вiдрiзку Р₂Р₃ i продовженням вiдрiзку Р₁Р₂ i перший шматок ламаноi Р₁Р₂Р₃Р₄тАж - Р₁Р₂Р₃ тАУ нами випрямлений. Тепер вiдобразимо другий (отриманий з Q при першому вiддзеркаленнi) багатокутник Q₁ щодо тiii його сторони, на якiй лежить наступна точка зламу Р₃′. Отримаiмо наступний багатокутник Q₂, i образ ланки Р₃′ Р₄′ при новому вiддзеркаленнi буде, знову-таки, продовженням вiдрiзка P₁P₂P'. Продовжуючи так i далi, ми можемо будь-який шматок ламаноi P₁P₂P₃P₄- . . ВлвипрямитиВ», тобто послiдовними вiддзеркаленнями перетворити в вiдрiзок прямоi P₁P₂P₃'P₄'

Звичайно, для рiзних траiкторiй прийдеться робить рiзнi послiдовностi випрямляючих вiддзеркалень. Проте якщо ми розглядаiмо бiльярд в прямокутнику, ми можемо iз самого початку з допомогою вiддзеркаленнi замостити всю площину прямокутниками, рiвними даному, отримавши грати з прямокутникiв. Намалювавши на цiй площинi довiльний промiнь, що не проходить нi через одну з вершин отриманих прямокутникiв, ми можемо за допомогою процедури, зворотноi описаноi, ВлскластиВ» цей промiнь в траiкторiю бiльярда в початковому прямокутнику ABCD. При такому ВлскладаннiВ» ТСрат прямокутникiв в початковий прямокутник ABCD в кожну точку М прямокутника ABCD потрапляi нескiнченно багато точок М_m,nплощинитАФ саме всi тi крапки якi виходять з М описаними вище вiддзеркаленнями.

Якщо траiкторiя, що виходить з точки М пiд кутом α до сторони AB, перiодична, то це значить, що пiсля випрямляння з цiii траiкторii вийде пряма, що проходить через М i через одну з крапок М_m,n. Якщо нумерувати крапки М_m,n iндексами m i n, то крапка М_m0,n0 повинна бути такою, що m₀ та n₀ тАФ парнi числа. Саме (i лише) в цьому випадку бiльярдна куля проходить через ту ж крапку М пiд колишнiм кутом α: номери m₀ та n₀ показують, скiльки потрiбне зробити вiддзеркалень щодо вертикальних i горизонтальних сторiн прямокутникiв, щоб отримати з крапки М_m0,n0 крапку М; при цьому непарне число вiддзеркалень мiняi напрям, парний же тАФ не мiняi.

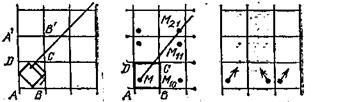
Доведемо, що неособлива траiкторiя, що виходить з крапки М прямокутника ABCD пiд кутом α до сторони AВ, перiодична в тому i лише б тому випадку, коли тангенс ii кута нахилу k=tga вимiрний з вiдношенням сторiн а1/а2 прямокутника ABCD.

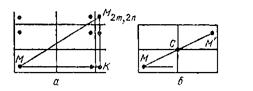
Дiйсно, тiльки що було з'ясовано, що перiодичнi тi i лише тi траiкторii, якi (пiсля випрямлення) вiдповiдають прямим, що йдуть з точки М в одну з точок виду М_2m,2n. Зауважу, що точка М_2m,2n отримуiться з М зсувом на вектор 2mВ·АВ + 2В·AD (*) так, що ΔМ М_2m,2n К маi катети з довжинами MK=2ma₁ i М_2m,2nК=2na_2. Таким чином k=tgα=2ma₁/2na₂=m/n В·a₂/a₁, тобто k вимiрне з a₂/a_1. Навпаки, якщо число k вимiрне з a₂/a_1, тобто k= m/n В·a₂/a_1, то будь-яка пряма, що виходить з точки М з тангенсом кута нахилу k, проходить через точку, що отримуiться з М зсувом на вектор (*), тобто через точку М_2m,2n .Якщо ця пряма не проходить через вершини прямокутникiв, то iй вiдповiдаi неособлива перiодична траiкторiя, що й потрiбне було довести.

Зазначу, що в даному випадку ми все-таки можемо продовжити i будь-яку особливу, тобто таку, що закiнчуiться в однiй з вершин прямокутника, - траiкторiю за цю вершину: нiщо не заважаi на площинi, замощенiй нашими прямокутниками, продовжити, наприклад, МС за вершину С i вважати тим самим, що, потрапивши у вершину С, бiльярдна куля вилiтаi з неi по тому ж шляху, по якому вiн туди залетiв - пiсля вiдповiдних вiддзеркалень промiнь СМ′ поiднуiться з променем СМ. Таким чином, у разi бiльярда в прямокутнику можна вважати, що рух по будь-якiй траiкторii продовжуiться необмежено в часi (наприклад, двiчi прохiдна дiагональ АС прямокутника тАФ це перiодична траiкторiя).

З доведеного твердження виходить:

Теорема 1. Якщо тангенс кута нахилу до траiкторiй вимiрний з числом k₀=a₂/a₁ то незалежно вiд початкового положення бiльярдноi кулi його рух буде перiодичним; в противному випадку траiкторiя неперiодична.

З допомогою теореми 1 можна по початковiй ланцi траiкторii кулi визначати, чи i ця траiкторiя перiодичноi або неперiодичноi. Для цього треба знайти вiдношення довжин сторiн прямокутника або, що те ж саме, тангенс кута нахилу дiагоналi прямокутника i тангенс кута, пiд яким запущена кулька, i подiлити перше число на друге: якщо в результатi вийде рацiональне число, то траiкторiя перiодична, якщо ж тАФ iррацiональне, то неперiодична. Звiдси слiдуi також i та обставина, що для фiксованого початкового вектора швидкостi кулi траiкторiя буде перiодичною або неперiодичною незалежно вiд його початкового положення на прямокутному столi. Тому, якщо запустити паралельно один одному вiдразу декiлька бiльярдних шарiв, вони або одночасно опишуть перiодичнi траiкторii, або нiколи не пройдуть по своiму старому слiду. Послiдовнiсть вiддзеркалень цих куль вiд бортiв бiльярда буде рiзною, якщо вони знаходяться достатньо далеко один вiд одного. Якщо ж кулi знаходяться достатньо близько, то послiдовнiсть бортiв, вiд яких вони вiддзеркалюються, буде однiiю i тiiю ж. Якщо першу ланку траiкторii однiii бiльярдноi кулi оточити паралельними ланками цiлого сiмейства траiкторiй iнших куль, то отриманi траiкторii, у разi, коли вони перiодичнi, заповнять самоперетинаючийся ВлкоридорВ». Таким чином, знаючи одну перiодичну траiкторiю, ми паралельним зсувом ii ланок одержуiмо iншу перiодичну траiкторiю.

Задача а) Довести, що у всiх неособливих Влпаралельних перiодичних траiкторiйВ» в прямокутнику рiвне число ланок i рiвнi довжини б) Довести, що в прямокутнику iснують скiльки завгодно довгi перiодичнi траiкторii.

Рiшення. Це виходить з розгляду випрямлених траiкторiй, що зображаються на ТСратах прямокутникiв рiвними паралельними вiдрiзками.

Як же поводиться на прямокутному столi неперiодична бiльярдна траiкторiя? В крузi i елiпсi неперiодична траiкторiя не заходила в деякi дiлянки тАФ в концентричний круг i, вiдповiдно, в софокусний елiпс (або в криволiнiйнi сегменти софокусноi гiперболи), проте заповнювала усюди щiльно кiльце мiж iх межами. В прямокутнику вона вже заходить в усi його дiлянки i заповнюi його усюди щiльно, В цьому i полягаi основний результат про неперiодичнi траiкторii в прямокутному бiльярдi.

Теорема 2. Якщо k/k₀ тАФ iррацiональне число, то будь-яка траiкторiя з кутовим коефiцiiнтом k усюди щiльно заповнюi весь прямокутник, тобто перетинаi будь-який (скiльки завгодно малий) круг, що лежить усерединi нього.

Таким чином, якщо точкову бiльярдну кулю запустити з будь-якого положення М в будь-якому напрямi α такому, що число tgα/tgφ iррацiональну, де φ тАФ кут нахилу дiагоналi до горизонтальноi сторони, то вiн рано чи пiзно зiткнеться з iншим, вже неточковою бiльярдною кулею (диском) N, куди б ми його нi поставили i скiльки б малий вiн був! Отже, гравцям (у разi вiдсутностi тертя) не потрiбно особливо старатися, щоб потрапити в iншу кулю (або лузу!), треба лише мати терпiння i час, щоб дочекатися потрiбного зiткнення.

Проблема побудови траiкторiй бiльярдiв в багатокутниках

Особливий клас утворюють бiльярди в многокутних i багатогранних областях. Цi областi характеризуються тим, що у кожноi дiльницi межi ðQ тАУ сторони многокутника або гранi багатогранника тАУ вектор нормалi ‍ň один i той же для всiх точок цiii дiльницi. Внаслiдок цього паралельний пучок бiллiардних траiкторiй, вiдбившись вiдсторони (гранi) остаiться паралельним. Для многокутних бiльярдiв маiться один елементарний, але водночас потужний геометричний прийом, так званий Влприйом барона МюнхаузенаВ», що значно спрощуi дослiдження. (ВлПрийом барона МюнхаузенаВ» - це метод випрямлення бiльярдних траiкторiй, що наводився ранiше. А саме, береться бiльярдна куля О (як у барона Мюнхаузена тАУ гарматне ядро) i, озброiвшись системою координат, спрямував вiсь Оу в напрямку руху, а вiсь Ох тАУ вправо, перпендикулярно осi Оу). Метод випрямлення бiльярдних траiкторiй в многокутнику належить нiмецькому математику Г.А. Шварцу (1843-1921). Але i перешкода, iз-за якоi картина поведiнки в многокутнику виявляiться досi непростою. Це тАУ вершини многокутника (а у багатогранникiв - ребро).

Не менш цiкавi i складнi питання, повтАЩязанi з перiодичними i всюди щiльними траiкторiями в многокутниках. Як приклад: вже в деяких трикутних областях мiнiмальна кiлькiсть ланок перiодичних траiкторiй може бути як завгодно велике. В випуклих областях дii теорема Биркгофа. В випуклiй областi Q з гладкою межою iснуi перiодична траiкторiя з будь-якою кiлькiстю ланок n≥2 (достатньо вписати в Q ламану максимальноi довжини з заданоi кiлькiстю ланок).

Вместе с этим смотрят:

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов