Матрицы и определители
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
СОДЕРЖАНИЕ
Лекция 1. Матрицы
1. Понятие матрицы. Типы матриц
2. Алгебра матриц
Лекция 2. Определители
1. Определители квадратной матрицы и их свойства
2. Теоремы Лапласа и аннулирования
Лекция 3. Обратная матрица
1. Понятие обратной матрицы. Единственность обратной матрицы
2. Алгоритм построения обратной матрицы. Свойства обратной матрицы
4. Задачи и упражнения
4.1. Матрицы и действия над ними
4.2. Определители
4.3. Обратная матрица
5. Индивидуальные задания
Литература
ЛЕКЦИЯ 1.МАТРИЦЫ
План
1. Понятие матрицы. Типы матриц.
2. Алгебра матриц.
Ключевые понятия
Диагональная матрица.
Единичная матрица.
Нулевая матрица.
Симметричная матрица.
Согласованность матриц.
Транспонирование.
Треугольная матрица.
1. ПОНЯТИЕ МАТРИЦЫ. ТИПЫ МАТРИЦ
Прямоугольную таблицу
А=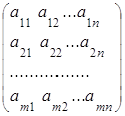 ,
,
состоящую из m строк и n столбцов, элементами которой являются действительные числа 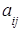 , где iтАУ номер строки, j- номер столбца на пересечении которых стоит этот элемент, будем называть числовой матрицей порядка m´n и обозначать
, где iтАУ номер строки, j- номер столбца на пересечении которых стоит этот элемент, будем называть числовой матрицей порядка m´n и обозначать 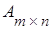 .
.
Рассмотрим основные типы матриц:
1. Пусть m = n, тогда матрица А тАУ квадратная матрица, которая имеет порядок n:
А = 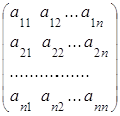 .
.
Элементы 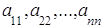 образуют главную диагональ, элементы
образуют главную диагональ, элементы 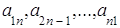 образуют побочную диагональ.
образуют побочную диагональ.
Квадратная матрица называется диагональной, если все ее элементы, кроме, возможно, элементов главной диагонали, равны нулю:
А = 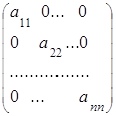 = diag (
= diag (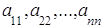 ).
).
Диагональная, а значит квадратная, матрица называется единичной, если все элементы главной диагонали равны 1:
Е = 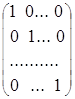 = diag (1, 1, 1,тАж,1).
= diag (1, 1, 1,тАж,1).
Заметим, что единичная матрица является матричным аналогом единицы во множестве действительных чисел, а также подчеркнем, что единичная матрица определяется только для квадратных матриц.
Приведем примеры единичных матриц:
 =
=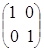 ,
,  =
=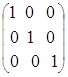 .
.
Квадратные матрицы
А = 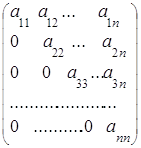 , В =
, В = 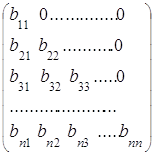
называются верхней и нижней треугольными соответственно.
2. Пусть m = 1, тогда матрица А тАУ матрица-строка, которая имеет вид:
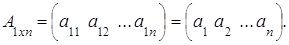
3. Пусть n=1, тогда матрица А тАУ матрица-столбец, которая имеет вид:
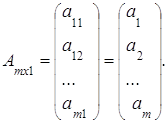
4.Нулевой матрицей называется матрица порядка m´n, все элементы которой равны 0:
0 = 
Заметим, что нулевая матрица может быть квадратной, матрицей-строкой или матрицей-столбцом. Нулевая матрица есть матричный аналог нуля во множестве действительных чисел.
5. Матрица называется транспонированнойк матрице 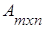 и обозначается
и обозначается 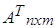 , если ее столбцы являются соответствующими по номеру строками матрицы
, если ее столбцы являются соответствующими по номеру строками матрицы 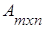 .
.
Пример. Пусть
Пусть 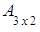 =
= 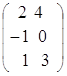 , тогда
, тогда 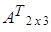 =
= 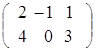 .
.
Заметим, если матрица А имеет порядок m´n, то транспонированная матрица имеет порядок n´m.
6. Матрица А называется симметричной, если А=А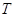 , и кососимметричной, если А = тАУА
, и кососимметричной, если А = тАУА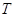 .
.
Пример. Исследовать на симметричность матрицы А и В.
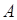 =
= 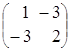 , тогда
, тогда 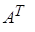 =
= 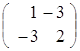 , следовательно, матрица А тАУ симметричная, так как А = А
, следовательно, матрица А тАУ симметричная, так как А = А .
.
В = 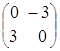 , тогда
, тогда 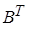 =
= 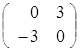 , следовательно, матрица В тАУ кососимметричная, так как В = тАУ В
, следовательно, матрица В тАУ кососимметричная, так как В = тАУ В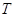 .
.
Заметим, что симметричная и кососимметричная матрицы всегда квадратные. На главной диагонали симметричной матрицы могут стоять любые элементы, а симметрично относительно главной диагонали должны стоять одинаковые элементы, то есть 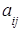 =
=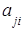 . На главной диагонали кососимметричной матрицы всегда стоят нули, а симметрично относительно главной диагонали
. На главной диагонали кососимметричной матрицы всегда стоят нули, а симметрично относительно главной диагонали 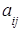 = тАУ
= тАУ 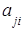 .
.
2. АЛГЕБРА МАТРИЦ
Рассмотрим действия над матрицами, но вначале введем несколько новых понятий.
Две матрицы А и В называются матрицами одного порядка, если они имеют одинаковое количество строк и одинаковое количество столбцов.
Пример.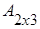 и
и 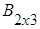 тАУ матрицы одного порядка 2´3;
тАУ матрицы одного порядка 2´3;
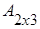 и
и 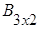 тАУ матрицы разных порядков, так как 2´3≠3´2.
тАУ матрицы разных порядков, так как 2´3≠3´2.
Понятия ″больше″ и ″меньше″ для матриц не определяют.
Матрицы А и В называются равными, если они одного порядка m´n, и 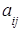 =
= 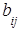 , где
, где 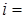 1, 2, 3, тАж, m, а j = 1, 2, 3, тАж, n.
1, 2, 3, тАж, m, а j = 1, 2, 3, тАж, n.
Умножение матрицы на число.
Умножение матрицы А на число λ приводит к умножению каждого элемента матрицы на число λ:
λА = 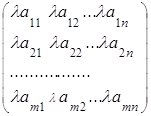 , λ
, λ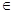 R.
R.
Из данного определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример.
Пусть матрица А =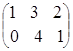 , тогда 5А=
, тогда 5А=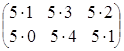 =
=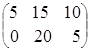 .
.
Пусть матрица В = 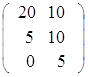 =
= 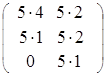 = 5
= 5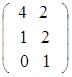 .
.
Свойства умножения матрицы на число:
1) λА = Аλ;
2) (λμ)А = λ(μА) = μ(λА), где λ,μ 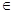 R;
R;
3) (λА)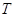 = λА
= λА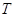 ;
;
4) 0ּА = 0.
Сумма (разность) матриц.
Сумма (разность) определяется лишь для матриц одного порядка m´n.
Суммой (разностью) двух матриц А и В порядка m´n называется матрица С того же порядка, где 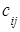 =
= 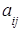 В±
В± 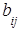 (
(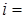 1, 2, 3, тАж, m ,
1, 2, 3, тАж, m ,
j = 1, 2, 3, тАж, n.).
Иными словами, матрица С состоит из элементов, равных сумме (разности) соответствующих элементов матриц А и В.
Пример. Найти сумму и разность матриц А и В.
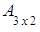 =
= 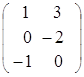 ,
, 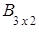 =
= 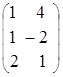 ,
,
тогда  =
= +
+ =
=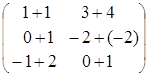 =
=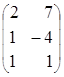 ,
,
 =
= тАУ
тАУ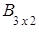 =
=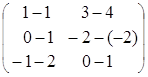 =
=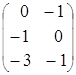 .
.
Если же 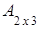 =
= 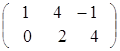 ,
, 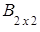 =
= 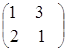 , то А В± В не существует, так как матрицы разного порядка.
, то А В± В не существует, так как матрицы разного порядка.
Из данных выше определений следуют свойства суммы матриц:
1) коммутативность А+В=В+А;
2) ассоциативность (А+В)+С=А+(В+С);
3) дистрибутивность к умножению на число λ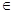 R: λ(А+В) = λА+λВ;
R: λ(А+В) = λА+λВ;
4) 0+А=А, где 0 тАУ нулевая матрица;
5) А+(тАУА)=0, где (тАУА) тАУ матрица, противоположная матрице А;
6) (А+В)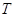 = А
= А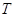 + В
+ В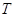 .
.
Произведение матриц.
Операция произведения определяется не для всех матриц, а лишь для согласованных.
Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В. Так, если 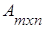 ,
, 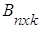 , m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если
, m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если 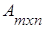 , а
, а 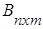 , то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
, то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
Произведением двух согласованных матриц 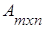 и
и 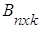
А=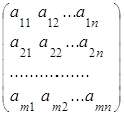 , В=
, В=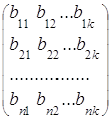
называется матрица С порядка m´k:
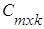 =
=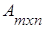 ∙
∙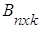 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
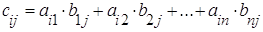 (
(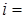 1, 2, 3, тАж, m , j=1, 2, 3, тАж, k),
1, 2, 3, тАж, m , j=1, 2, 3, тАж, k),
то есть элемент 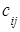 i тАУой строки и j тАУго столбца матрицы С равен сумме произведений всех элементов i тАУой строки матрицы А на соответствующие элементы j тАУго столбца матрицы В.
i тАУой строки и j тАУго столбца матрицы С равен сумме произведений всех элементов i тАУой строки матрицы А на соответствующие элементы j тАУго столбца матрицы В.
Пример. Найти произведение матриц А и В.
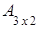 =
=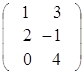 ,
, 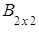 =
=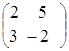 ,
,
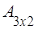 ∙
∙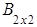 =
=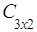 =
=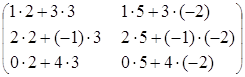 =
=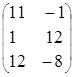 .
.
Произведение матриц В∙А не существует, так как матрицы В и А не согласованы: матрица В имеет порядок 2´2, а матрица А тАУ порядок 3´2.
Рассмотрим свойства произведения матриц:
1) некоммутативность: АВ ≠ ВА, даже если А и В, и В и А согласованы. Если же АВ = ВА, то матрицы А и В называются коммутирующими (матрицы А и В в этом случае обязательно будут квадратными).
Пример 1. 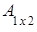 =
= 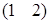 ,
, 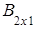 =
= 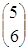 ;
;
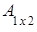
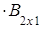 =
=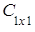 =
=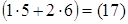 ;
;
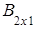
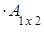 =
=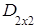 =
=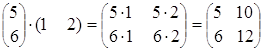 .
.
Очевидно, что  ≠
≠ 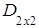 .
.
Пример 2.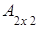 =
= 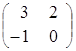 ,
, 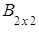 =
= 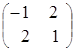 ;
;
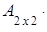
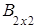 =
= 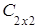 =
= 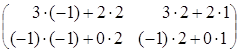 =
=
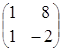 ;
;
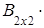
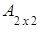 =
= 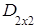 =
= 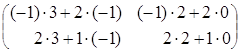 =
=  .
.
Вывод: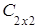 ≠
≠ , хотя матрицы
, хотя матрицы  и
и 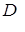 одного порядка.
одного порядка.
2) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.
Пример.
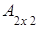 =
=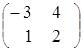 ,
, 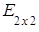 =
=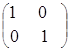 ;
;
 =
=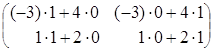 =
=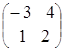 =
=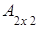 ;
;
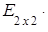
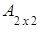 =
=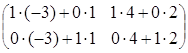 =
=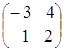 =
= .
.
3) A·0 = 0·A = 0.
4) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.
Пример.
 =
= 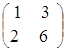 ,
, 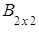 =
= 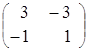 ;
;
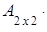
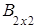 =
= 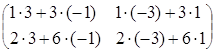 =
=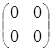 =
= .
.
5) ассоциативность АВС=А(ВС)=(АВ)С:
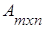 · (
· (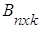 ·
·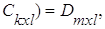
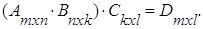
Пример.
Имеем матрицы 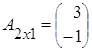 ,
, 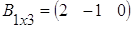 ,
, 
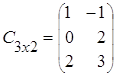 ;
;
тогда Аּ(ВּС) = 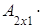 (
(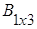 ·
·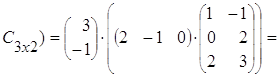
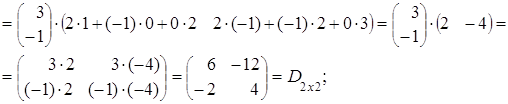
(АּВ)ּС=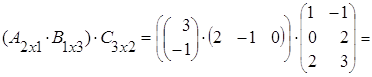
=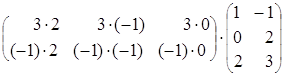 =
=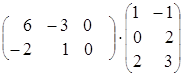 =
=
=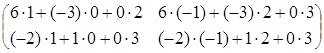 =
=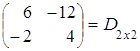 .
.
Таким образом, мы на примере показали, что Аּ(ВּС) = (АּВ)ּС.
6) дистрибутивность относительно сложения:
(А+В)∙С = АС + ВС, А∙(В + С)=АВ + АС.
7) (А∙В)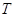 = В
= В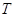 ∙А
∙А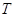 .
.
Пример.
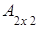 =
=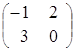 ,
, 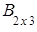 =
=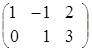 ,
,
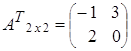 ,
, 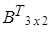 =
=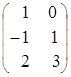 .
.
Тогда АВ=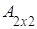 ∙
∙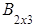 =
=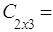
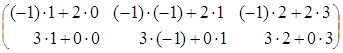 =
=
=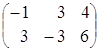
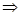 (А∙В)
(А∙В)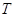 =
= 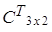 =
=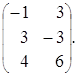
В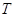 ∙А
∙А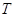 =
=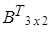 ∙
∙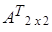 =
= 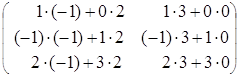 =
=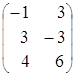 =
=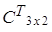 .
.
Таким образом, (А∙В)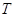 = В
= В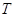 А
А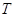 .
.
8) λ(АּВ) = (λА)ּ В = Аּ (λВ), λ,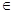 R.
R.
Рассмотрим типовые примеры на выполнение действий над матрицами, то есть требуется найти сумму, разность, произведение (если они существуют) двух матриц А и В.
Пример 1.
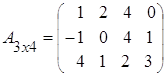 ,
, 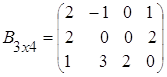 .
.
Решение.
1) 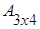 +
+ 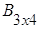 =
= 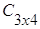 =
= 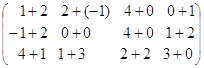 =
=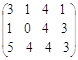 ;
;
2) тАУ
тАУ  =
= =
=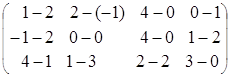 =
=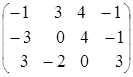 ;
;
3) произведение 
 не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения
не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения 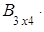
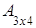 по той же причине.
по той же причине.
Пример 2.
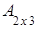 =
=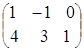 ,
, 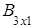 =
=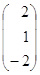 .
.
Решение.
1) суммы матриц, как и их разности, не существует, так как исходные матрицы разного порядка: матрица А имеет порядок 2´3, а матрица В тАУ порядок 3´1;
2) так как матрицы А и В согласованны, то произведение матриц АּВ существует:
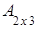 ·
·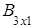 =
=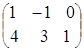 ·
·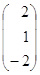 =
=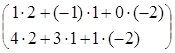 =
=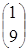 ,
,
произведение матриц ВּА не существует, так как матрицы 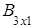 и
и 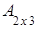 несогласованны.
несогласованны.
Пример 3.
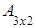 =
=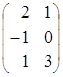 ,
, 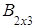 =
=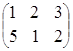 .
.
Решение.
1) суммы матриц, как и их разности, не существует, так как исходные матрицы разного порядка: матрица А имеет порядок 3´2, а матрица В тАУ порядок 2´3;
2) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны, но результатом таких произведений будут матрицы разных порядков: 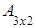 ·
·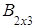 =
=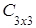 ,
, 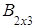 ·
·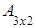 =
=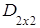 .
.
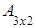 ·
·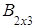 =
=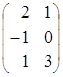 ·
·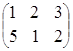 =
=
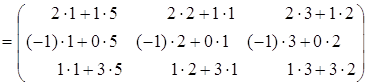 =
= 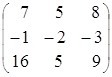 =
=  ;
;
 ·
·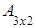 =
=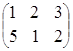 ·
·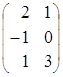 =
=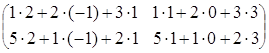 =
=
= 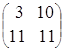 =
=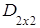
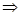 в данном случае АВ ≠ ВА.
в данном случае АВ ≠ ВА.
Пример 4.
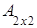 =
=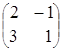 ,
,  =
=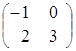 .
.
Решение.
1)  +
+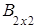 =
=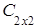 =
=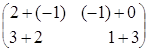 =
=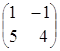 ,
,
2) 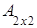 тАУ
тАУ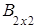 =
= 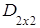 =
=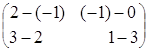 =
=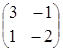 ;
;
3) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны:
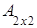 ·
·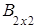 =
=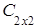 =
=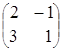 ·
·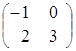 =
=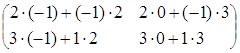 =
=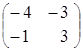 ;
;
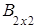 ·
·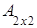 =
=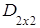 =
=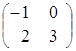 ·
·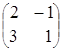 =
=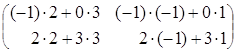 =
=
=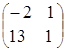
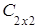 ≠
≠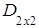 , то есть матрицы А и В некоммутирующие.
, то есть матрицы А и В некоммутирующие.
Пример 5.
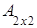 =
=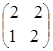 ,
, 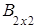 =
=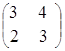 .
.
Решение.
1) 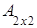 +
+ =
=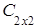 =
= =
=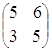 ,
,
2)  тАУ
тАУ =
=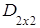 =
=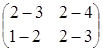 =
=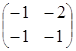 ;
;
3) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны:
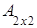 ·
·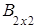 =
=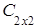 =
=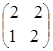 ·
·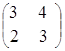 =
=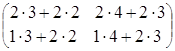 =
=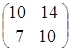 ;
;
 ·
· =
=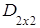 =
=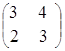 ·
·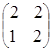 =
=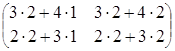 =
=
=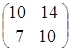
 =
=
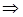 АּВ=ВּА, т. е. данные матрицы коммутирующие.
АּВ=ВּА, т. е. данные матрицы коммутирующие.
ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ
План
1. Определители квадратной матрицы и их свойства.
2. Теоремы Лапласа и аннулирования.
Ключевые понятия
Алгебраическое дополнение элемента определителя.
Минор элемента определителя.
Определитель второго порядка.
Определитель третьего порядка.
Определитель произвольного порядка.
Теорема Лапласа.
Теорема аннулирования.
1. ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА
Пусть А тАУ квадратная матрица порядка n:
А=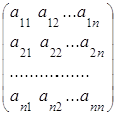 .
.
Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое
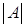 = det A= Δ=
= det A= Δ=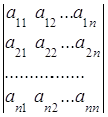 .
.
Отметим, что определитель существует только для квадратных матриц.
Рассмотрим правила вычисления определителей и их свойства для квадратных матриц второго и третьего порядка, которые будем называть для краткости определителями второго и третьего порядка соответственно.
Определителем второго порядкаматрицы 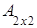 называется число, определяемое по правилу:
называется число, определяемое по правилу:
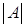 =
=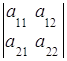 =
=
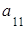
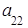 тАУ
тАУ 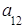
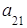 , (1)
, (1)
т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Пример.
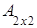 =
=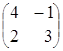 , тогда
, тогда 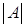 =
=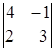 = 4 В· 3 тАУ ( тАУ1) В· 2=12 + 2 = 14.
= 4 В· 3 тАУ ( тАУ1) В· 2=12 + 2 = 14.
Следует помнить, что для обозначения матриц используют круглые или квадратные скобки, а для определителя тАУ вертикальные линии. Матрица тАУ это таблица чисел, а определитель тАУ число.
Из определения определителя второго порядка следуют его свойства:
1. Определитель не изменится при замене всех его строк соответствующими столбцами:
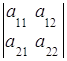 =
=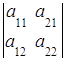 .
.
2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
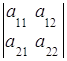 = тАУ
= тАУ 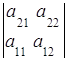 ,
, 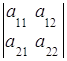 = тАУ
= тАУ 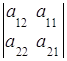 .
.
3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
 =
=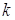
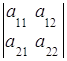 или
или 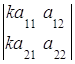 =
=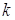
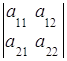 .
.
4. Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю.
5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
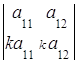 =0,
=0, 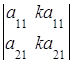 = 0.
= 0.
6. Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей:
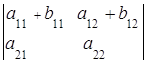 =
=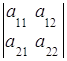 +
+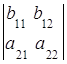 ,
,  =
=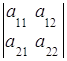 +
+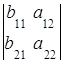 .
.
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число 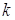 :
:
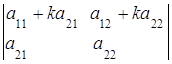 =
=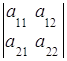 +
+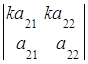 =
=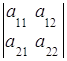 ,
,
так как 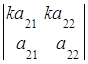 =0 по свойству 5.
=0 по свойству 5.
Остальные свойства определителей рассмотрим ниже.
Введем понятие определителя третьего порядка: определителем третьегопорядкаквадратной матрицы называется число
Δ =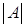 = det A=
= det A= 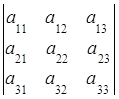 =
=
=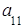
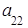
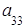 +
+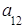
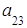
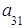 +
+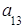
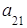
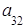 тАУ
тАУ 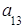
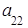
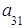 тАУ
тАУ 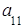
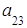
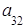 тАУ
тАУ 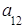
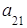
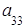 ,
,
(2)
т. е. каждое слагаемое в формуле (2) представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения в формуле (2) брать со знаком плюс, а какие со знаком минус, полезно знать правило треугольников (правило Саррюса):
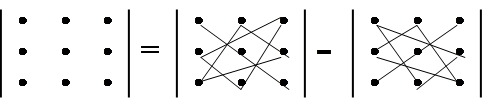
Пример. Вычислить определитель
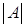 =
=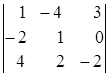 =
=
=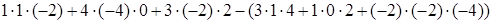 =
=
=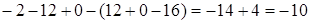 .
.
Следует отметить, что свойства определителя второго порядка, рассмотренные выше, без изменений переносятся на случай определителей любого порядка, в том числе и третьего.
2. ТЕОРЕМЫ ЛАПЛАСА И АННУЛИРОВАНИЯ
Рассмотрим еще два очень важных свойства определителей.
Введем понятия минора и алгебраического дополнения.
Минором элемента определителя называется определитель, полученный из исходного определителя вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Обозначают минор элемента 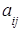 через
через 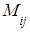 .
.
Пример.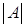 =
= 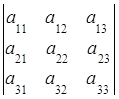 .
.
Тогда, например, 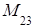 =
= 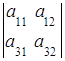 ,
, 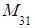 =
= 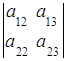 .
.
Алгебраическим дополнением элемента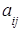 определителя
определителя 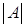 называется его минор
называется его минор 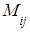 , взятый со знаком
, взятый со знаком 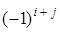 . Алгебраическое дополнение будем обозначать
. Алгебраическое дополнение будем обозначать 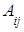 , то есть
, то есть 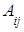 =
=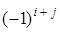
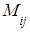 .
.
Например:
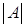 =
= 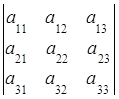 ,
, 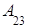 =
=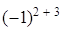
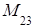 =
=
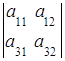 = тАУ
= тАУ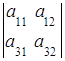 ,
,
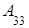 =
=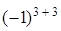
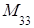 =
=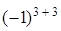
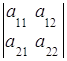 =
=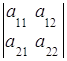 .
.
Вернемся к формуле (2). Группируя элементы и вынося за скобки общий множитель, получим:
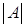 =
=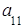 (
(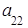
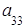 тАУ
тАУ 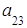
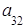 ) +
) +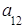 (
(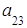
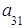 тАУ
тАУ 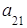
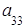 ) +
) +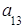 (
(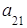
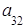 тАУ
тАУ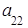
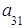 )=
)=
= 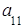 ּ
ּ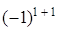
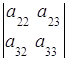 +
+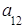 ּ
ּ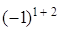
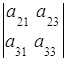 +
+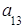 ּ
ּ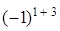
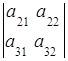 =
=
= 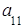
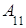 +
+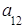
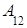 +
+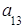
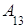 .
.
Аналогично доказываются равенства:
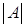 =
=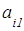
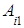 +
+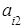
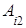 +
+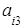
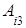 ,
, 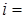 1, 2, 3; (3)
1, 2, 3; (3)
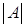 =
=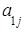
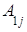 +
+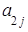
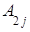 +
+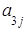
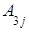 ,
, 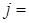 1, 2, 3.
1, 2, 3.
Формулы (3) называются формулами разложения определителя по элементам i-ой строки (j-го столбца), или формулами Лапласа для определителя третьего порядка.
Таким образом, мы получаем восьмое свойство определителя:
Теорема Лапласа. Определитель равен сумме всех произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца).
Заметим, что данное свойство определителя есть не что иное, как определение определителя любого порядка. На практике его используют для вычисления определителя любого порядка. Как правило, прежде чем вычислять определитель, используя свойства 1 тАУ 7, добиваются того, если это возможно, чтобы в какой-либо строке (столбце) были равны нулю все элементы, кроме одного, а затем раскладывают по элементам строки (столбца).
Пример. Вычислить определитель
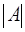 =
=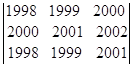 = (из второй строки вычтем первую) =
= (из второй строки вычтем первую) =
=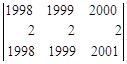 = (из третьей строки вычтем первую)=
= (из третьей строки вычтем первую)=
=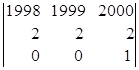 = (разложим определитель по элементам третьей
= (разложим определитель по элементам третьей
строки) = 1ּ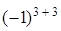
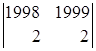 = (из второго столбца вычтем первый столбец) =
= (из второго столбца вычтем первый столбец) = 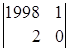 = 1998ּ0 тАУ 1ּ2 = тАУ2.
= 1998ּ0 тАУ 1ּ2 = тАУ2.
Пример.
Рассмотрим определитель четвертого порядка. Для его вычисления воспользуемся теоремой Лапласа, то есть разложением по элементам строки (столбца).
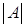 =
=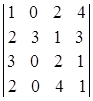 = (так как второй столбец содержит три нулевых элемента, то разложим определитель по элементам второго столбца)= =3ּ
= (так как второй столбец содержит три нулевых элемента, то разложим определитель по элементам второго столбца)= =3ּ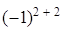
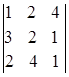 = (из второй строки вычтем первую, умноженную на 3, а из третьей строки вычтем первую, умноженную на 2) =
= (из второй строки вычтем первую, умноженную на 3, а из третьей строки вычтем первую, умноженную на 2) =
= 3ּ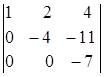 = (разложим определитель по элементам первого столбца) = 3ּ1ּ
= (разложим определитель по элементам первого столбца) = 3ּ1ּ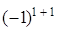
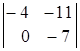 =
= 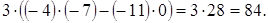
Девятое свойствоопределителяносит название теорема аннулирования:
сумма всех произведений элементов одной строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю, то есть
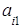
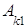 +
+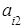
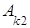 +
+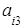
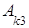 = 0,
= 0, 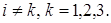
Пример.
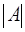 =
= 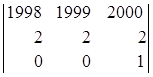 = (разложим по элементам третьей строки)=
= (разложим по элементам третьей строки)=
= 0ּ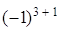
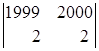 +0ּ
+0ּ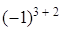
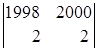 +
+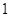 ּ
ּ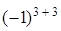
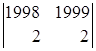 = тАУ2.
= тАУ2.
Но, для этого же примера: 0ּ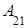 +0ּ
+0ּ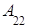 +1ּ
+1ּ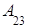 =
=
= 0ּ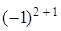
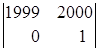 +0ּ
+0ּ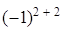
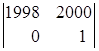 +1ּ
+1ּ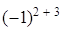
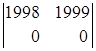 = 0.
= 0.
Если определитель любого порядка имеет треугольный вид
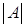 =
=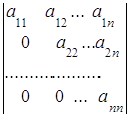 , то он равен произведению элементов, стоящих на диагонали:
, то он равен произведению элементов, стоящих на диагонали:
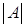 =
=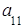 ּ
ּ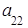 ּ тАж ּ
ּ тАж ּ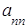 . (4)
. (4)
Пример. Вычислить определитель.
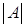 =
=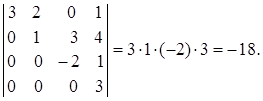
Иногда при вычислении определителя с помощью элементарных преобразований удается свести его к треугольному виду, после чего применяется формула (4).
Что касается определителя произведения двух квадратных матриц, то он равен произведению определителей этих квадратных матриц: 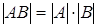 .
.
ЛЕКЦИЯ 3.ОБРАТНАЯ МАТРИЦА
План
1. Понятие обратной матрицы. Единственность обратной матрицы.
2. Алгоритм построения обратной матрицы.
Свойства обратной матрицы.
Ключевые понятия
Обратная матрица.
Присоединенная матрица.
1. ПОНЯТИЕ ОБРАТНОЙ МАТРИЦЫ.
ЕДИНСТВЕННОСТЬ ОБРАТНОЙ МАТРИЦЫ
В теории чисел наряду с числом 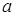 определяют число, противоположное ему (
определяют число, противоположное ему (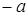 ) такое, что
) такое, что 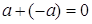 , и число, обратное ему
, и число, обратное ему 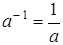 такое, что
такое, что 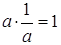 . Например, для числа 5 противоположным будет число
. Например, для числа 5 противоположным будет число
(тАУ 5), а обратным будет число 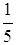 . Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (тАУ А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица
. Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (тАУ А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица 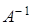 , если выполняются равенства
, если выполняются равенства
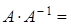
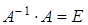 , (1)
, (1)
где Е тАУ единичная матрица порядка n.
Сразу же отметим, что обратная матрица существует только для квадратных невырожденных матриц.
Квадратная матрица называется невырожденной(неособенной), если det A ≠ 0. Если же det A = 0, то матрица А называется вырожденной(особенной).
Отметим, что невырожденная матрица А имеет единственную обратную матрицу 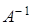 . Докажем это утверждение.
. Докажем это утверждение.
Пусть для матрицы А существует две обратные матрицы 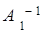 ,
,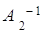 , то есть
, то есть
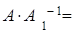
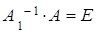 и
и 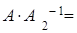
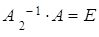 .
.
Тогда 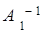 =
=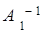 ּ
ּ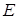 =
=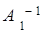 ּ(
ּ(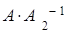 ) =
) =
= (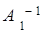 ּ
ּ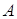 )
) 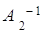 =
=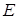
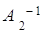 =
=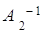
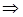
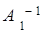 =
=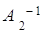 .
.
Что и требовалось доказать.
Найдем определитель обратной матрицы. Так как определитель произведения двух матриц А и В одинакового поряд
Вместе с этим смотрят:
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов