Метод векторiв та його застосування

Метод векторiв та його застосування

Вступ

Поняття вектора i одним iз фундаментальних понять сучасноi математики. Його можна визначити по-рiзному: як напрямлений вiдрiзок, як упорядковану пару точок, що i кiнцями напрямленого вiдрiзка, як множину однаково напрямлених вiдрiзкiв однаковоi довжини, як упорядковану пару чисел, як паралельне перенесення.

Уперше поняття вектора як напрямленого вiдрiзка знайшло застосування в механiцi для зображення фiзичних векторних величин: швидкостi, прискорення, сили, моменту сили тощо. Високий ступiнь наочностi i простота геометричних операцiй над векторами як напрямленими вiдрiзками сприяли тому, що поняття вектора знайшло загальне визнання i застосування в iнших роздiлах фiзики: в кiнематицi, статицi, динамiцi точки i динамiцi системи, в теорii потенцiалу та гiдродинамiцi, а також стало одним iз основних понять таких наук, як векторна алгебра, векторний аналiз, теорiя поля, тензорний аналiз тощо.

Проте хоча поняття вектора знайшло перше застосування в фiзицi, це математичне поняття, усi операцii над якими виконуються за законами математики.

Вектор як математичне поняття мiцно ввiйшов у шкiльну математику, у рiзнi нематематичнi науки. В школi за допомогою векторного метод розвтАЩязуiться багато рiзноманiтних задач, якi не мають iншого способу розвтАЩязання.

Саме тому вивчення поняття вектора i дуже важливим в сучасних умовах розвитку математичних наук.

1. Поняття вектора

В елементарнiй геометрii, як вiдомо, вiдрiзком AB називаiться сукупнiсть всiх точок прямоi, що лежать мiж A i B. Точки A i B називаються кiнцями вiдрiзка. При цьому, очевидно, порядок, в якому беруться кiнцi вiдрiзка, несуттiвий. Однак при використаннi геометрii у вивченнi фiзики, особливо механiки, часто доводиться розглядати напрямленi вiдрiзки, тобто вiдрiзки, для яких вказанi початкова i кiнцева точки. Тобто ABi BA геометрично один i той же вiдрiзок, то, розглядаючи iх як напрямленi вiдрiзки, ми повиннi враховувати, що вони задають рiзнi обтАЩiкти.

Означення 1. Вiдрiзок АВ називаiться напрямленим, якщо береться до уваги порядок його кiнцевих точок. Перша точка (А) називаiться його початком, а друга (В) тАУ його кiнцем.

Позначають напрямлений вiдрiзок так: АВ.

Означення 2. Довжиною напрямленого вiдрiзка називаiться

довжина вiдрiзка АВ. Позначають: . Звiдси = АВ=

Означення 3. Напрямленi вiдрiзки АВi CDназиваються однаково напрямленими (спiв напрямленими), якщо однаково напрямленi променi АВi CD, i протилежно напрямленими, якщо цi променi протилежно напрямленi.

Означення 4. Векторомназиваiться множина однаково напрямлених (спiв напрямлених) вiдрiзкiв однаковоi довжини.

Означення 4.1. Вектором називаiться напрямлений вiдрiзок, тобто вiдрiзок, для якого вказано, яка з обмежуючих його точок рахуiться першою, яка тАУ другою. Перша точка напрямленого вiдрiзка називаiться початком вектора, а друга точка тАУ кiнцем.

Напрямок вектора на кресленнi вiдмiчаiться стрiлкою, оберненою гострим кiнцем до кiнця вектора. В текстi вектор записуiться двома великими лiтерами латинського алфавiту зi спiльною рискою зверху, при цьому перша з них позначаi початок, друга тАУ кiнець вектора. Наприклад, , (мал. 1.a), причому А, C тАУ вiдповiдно початки, а В, D тАУ кiнцi даних векторiв. В деяких випадках вектор позначаiться також однiiю малою лiтерою, наприклад, a, , c,тАж (мал. 1.b).

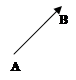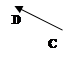мал. 1.aмал. 1.

Означення 5. Вектори i називаються однаково напрямленими(спiв напрямленими), якщо спiв напрямленi вiдповiднi iм напрямленi вiдрiзки i (мал. 2.a), i протилежно напрямленими, якщо напрямленi вiдрiзки i протилежно напрямленi (мал. 2.b).

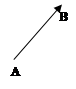
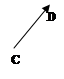
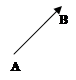
мал. 2.aмал. 2.

Означення 6. Довжиною (модулем) вектора називаiться довжина будь-якого представника класу спiв напрямлених вiдрiзкiв, який визначаi цей вектор.

РЖнакше кажучи, довжиною вектора називаiться довжина напрямного вiдрiзка, який зображаi цей вектор.

Модуль вектора позначають , а вектора АBтАУ .

Вектор, початок якого збiгаiться з його кiнцем, називаiться нульовим вектором, позначають або . Нульовий вектор не визначаi нiякого напряму, а його довжина вважаiться рiвною нулю.

Вектор, довжина якого дорiвнюi одиницi, називаiться одиничним вектором, або ортом.

Рiвнiсть векторiв

Означення 1. Два вектори називаються рiвними, якщо множини вiдповiдних iм напрямлених вiдрiзкiв збiгаються. Пишуть: =.

Всi нульовi вектори вважаться рiвними один одному.

РЖз цього означення випливаi така ознака рiвностi двох векторiв.

Теорема 1. (перша ознака рiвностi двох векторiв).

Для того щоб два вектори були рiвними, необхiдно i достатньо, щоб вони були однаково напрямленими i мали рiвнi довжини.

Доведення:

1. Необхiднiсть. Нехай вектори i рiвнi. Доведемо, що i =.

Якщо =, то, за означенням 1, множини напрямлених вiдрiзкiв, якi вiдповiдають цим векторам, збiгаються. Тому , =. Звiдси ,=, що й треба було довести.

2. Достатнiсть. Нехай , =. Доведемо, що =. Якщо, , =, то , =, тобто i належать однiй i тiй же множинi однаково напрямлених вiдрiзкiв рiвноi довжини. А це означаi, що =. Теорему доведено.

Наслiдок. Два вектори, кожен з яких дорiвнюi третьому, рiвнi мiж собою.

Теорема 2.(теорема про вiдкладання вектора).

Вiд будь-якоi точки простору можна вiдкласти вектор, рiвний даному, i до того ж iдиний.

Доведення: Нехай даний вектор зображаiться напрямленим вiдрiзком . Виберемо у просторi довiльну точку О, сполучимо точку Вз точкою Оi позначимо середину вiдрiзка ОВчерез С(мал. 3). Проведемо

вiдрiзок АС i вiдкладемо на його продовженнi вiдрiзок CM=АС. Чотирикутник АВМОi паралелограмом, бо його дiагоналi точкою перетину дiляться пополам. Звiдси випливаi, що променi АВi ОМоднаково напрямленi, а вiдрiзки АВi ОМрiвнi. Отже, ==.

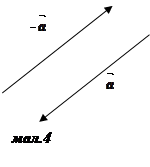
Доведемо тепер, що цей вектор iдиний. Припустимо, що iснуi iнший вектор =, вiдмiнний вiд . Але ж i =, тому =. Отже, , =, тому точки M i збiгаються, що суперечить припущенню. Тобто вiд точки O можна вiдкласти лише один вектор, рiвний даному вектору . Теорему доведено.

Означення 2. Два вектори називаються протилежними, якщо вони протилежно напрямленi i мають рiвнi довжини. Вектор, протилежний до , позначаiться - (мал. 4). Очевидно, =-, тАУ (-)=.

Додавання векторiв, властивостi операцii додавання векторiв

Введемо операцiю додавання векторiв, яка вiдiграi важливу роль в векторнiй алгебрi.

Означення. Нехай задано два вектори i . Вiд деякоi точки A вiдкладемо вектор =, потiм вiд точки B вiдкладемо вектор =. Вектор = називаiться сумою векторiв i i позначаiться так: =+ (мал. 5). Помiтимо, що для знаходження двох неколiнеарних векторiв доводиться будувати трикутник. Тому вказане правило додавання векторiв називають правилом трикутника.Це правило можна сформулювати так: для будь-яких трьох точок A,B iC+=, або: сумою векторiв i iвектор , який сполучаi початок вектора з кiнцем вектора при умовi, що вектор вiдкладено вiд кiнця вектора .

З цього правила випливаi правило паралелограма: якщо вектори i вiдкладенi вiд спiльного початку O, =, = (мал. 6) i на них побудовано паралелограм OACB, то сумою векторiв + i вектор =, який виходить з того ж початку i збiгаiться з дiагоналлю OC паралелограма.

Розглянемо властивостi операцii додавання векторiв.

Властивiсть 1. Операцiя додавання векторiв комутативна, тобто для будь-яких векторiв i : +=+.

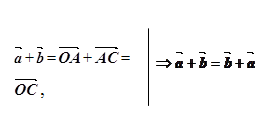Доведення: За правилом трикутника маiмо (мал. 7):

Властивiсть 2. Операцiя додавання векторiв асоцiативна, тобто для будь-яких векторiв , , : (+)+= +(+)

Доведення: Вiзьмемо довiльну точку Ai вiд неi вiдкладемо вектори =, =, = (мал. 8). Тодi +=, (+)+=; +=; +(+)=. Отже, (+)+ =+(+).

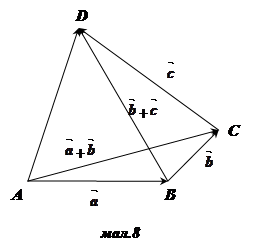
Властивiсть 3. Сумою протилежних векторiв i нуль-вектор: +(-)=0.

Доведення. Нехай =, тодi -=, i за правилом трикутника матимемо +(-)=+==0.

Властивiсть 4. Нуль-вектор i нейтральним елементом операцii додавання: +=+.

Доведення: Нехай =, =, тодi за правилом трикутника +=+==.

Знаведених властивостей додавання векторiв випливаi, що операцiя додавання векторiв маi тi ж властивостi, що й операцiя додавання чисел. Тому часто при перетвореннi сум векторiв дiiмо так само, як i при перетвореннi числових виразiв: (+)+=+(+)=(+)+=(+).

Сума бiльшоi кiлькостi векторiв знаходиться за правилом многокутника. Щоб знайти суму n векторiв (мал. 9), потрiбно з довiльноi точки O вiдкласти вектор =, з його кiнця тАУ вектор =,тАж,= (початок кожного наступного вектора-доданка i кiнцем попереднього). Вектор = буде сумою даних векторiв.

Вiднiмання векторiв

Операцiя вiднiмання векторiв вводиться як протилежна до додавання. Означення. Рiзницею векторiв i називаiться такий вектор , який в сумi з вектором даi вектор : -=якщо +=. /1/

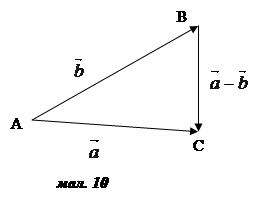
Доведемо, що вектор iснуi i притому iдиний. Припустимо, що вектор iснуi. Тодi, додавши до обох частин рiвностi вектор (-) i користуючись властивостями суми векторiв, маiмо: (-)++=(-)+. /2/

Отже, якщо вектор iснуi, то вiн визначаiться попередньою рiвнiстю /2/, а тому iдиний. Дiйсно, пiдставивши /2/ в /1/, одержимо правильну рiвнiсть: ++(-)=.

Отже, вектор, який визначаiться формулою /2/, i рiзницею векторiв i : -=+(-)=. За правилом трикутника +=. Звiдси
=- (мал. 10).

Отже, для побудови рiзницi векторiв i досить вiдкласти цi вектори вiд спiльного початку (=,=) i провести вектор вiд кiнця B вектора-вiдтАЩiмника до кiнцяCвектора-зменшуваного; цей вектор i i шуканою рiзницею -: =-.

Множення вектора на число

Означення. Добутком вектора на дiйсне число α називаiться вектор , який задовольняi такi умови:

1) =*;

2) , якщо α >0, i , якщо α <0.

Такий вектор позначаiться = α .

Операцiя добутку вектора на число маi такi властивостi.

Властивiсть 1. α*=0*= для будь-якого дiйсного числа α i будь-якого вектора . Ця властивiсть випливаi з умови 1) означення.

Властивiсть 2. Для будь-якого вектора 1*=; -1*=-. Ця властивiсть випливаi безпосередньо з означення.

Властивiсть 3. Для будь-якого вектора i будь-яких дiйсних чисел α i β: α(β)=(αβ) .

Доведення. Нехай α(β)=, (αβ) =. Доведемо, що =. Маiмо:

=*=**,

=*=**.

Отже, =. Покажемо, що . Якщо α i β одного знаку, то вектор однаково напрямлений з i однаково напрямлений з .Отже, . У випадку коли числа α i β протилежних знакiв, , . Отже, також , що й треба було довести.

Властивiсть 4. Операцiя множення вектора на число дистрибутивна вiдносно додавання векторiв, тобто α(+)=α+α, для , i α R.

Доведення. Нехай α > 0. Вiдкладемо вектори =, =, =α, =α (мал. 11). Тодi +=, α+α=. Покажемо, що =α. Оскiльки вектори i α , i α вiдповiдно однаково напрямленi, то вiдповiднi кути A i у трикутникiв OAB i рiвнi (як кути утворенi при перетинi двох паралельних прямих третьою). Крiм того, сторони цих трикутникiв, що прилягають до рiвних кутiв, пропорцiйнi: . Тому OAB~ . Звiдси випливаi, що OAB=, а це означаi, що променi OB i збiгаються, тобто . Крiм того =α*=*. Тому =α*.

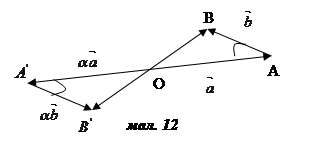
Аналогiчно розглядаiться випадок, коли α <0 (мал. 12).

Випадок α = 0 тривiальний. Отже, α (+) = α+α.

Властивiсть 5. Операцiя множення вектора на число дистрибутивна вiдносно додавання чисел, тобто (α+β)=α+β, i α, β R.

Доведення. Розглянемо два можливих випадки: αβ >0 i αβ <0 (випадок αβ=0 не викликаi труднощiв).

1. Нехай αβ >0, тобто числа α i β одного знаку. Тодi вектори (α+β) i α+β однаково напрямленi. Крiм того,

;

.

Отже, i вектори (α+β) та α+β рiвнi.

2. Нехай αβ <0, тобто числа α i β рiзних знакiв. Якщо α = -β, то (α+β)=(-β+β)=0=0; α+β= -β+ β=0, отже, властивiсть справджуiться.

Якщо α-β, тодi тАУα, α+β або тАУβ, α+β одного знаку. Нехай, наприклад, -α, α+β одного знаку. Тодi за доведеним (-α)+ (α+β)=(-α+α+β)=β(α+β)= α+β, що i треба було довести.

2. Колiнеарнiсть векторiв

Означення. Два ненульових вектори i називаiться колiнеарними, якщо вiдповiднi iм напрямленi вiдрiзки паралельнi або лежать на однiй прямiй.

Позначення: ||(мал. 13).

Очевидно, колiнеарнi вектори або однаково напрямленi (мал. 13а), або протилежно напрямленi (мал. 12b). Нульовий вектор вважаiться колiнеарним будь-якому вектору. Тому, якщо вiдомо, що деякi два вектори неколiнеарнi, то жоден з них не i нульовим вектором.

Теорема. (перша ознака колiнеарностi двох векторiв). Два ненульових вектори i колiнеарнi тодi i тiльки тодi, коли iснуi деяке число α таке, що =α. /1/

Доведення.

1. Необхiднiсть. Нехай ||. Тодi або , або . Якщо , то =, оскiльки цi вектори однаково напрямленi, то вони мають однаковi модулi: ==. Позначивши α =, дiстанемо =α. Якщо , то аналогiчно доводиться, що = -. Нехай α = -, тодi також = α.

2. Достатнiсть. Нехай виконуiться рiвнiсть /1/, тодi i або однаково, або протилежно напрямленi, а отже, вони колiнеарнi. Теорему доведено.

Зауваження 1. Якщо = 0, 0, то теорема також справджуiться. У цьому випадку α =0.

Зауваження 2. Оскiльки для колiнеарних векторiв i завжди iснуi тiльки одне число α таке, що = α , то звiдси формально можна написати: α =, тобто можна розглядати вiдношення двох колiнеарних векторiв.

Вiдношення :двох колiнеарних векторiв розумiють як число, на яке треба помножити вектор , щоб дiстати вектор . Отже, вiдношенням двох колiнеарних векторiв i число, яке дорiвнюi вiдношенню iх модулiв, взяте зi знаком ВлплюсВ», якщо вектори i однаково напрямленi, i зi знаком ВлмiнусВ», якщо вектори протилежно напрямленi.

3. Компланарнiсть векторiв

Означення. Три ненульових вектори називаються компланарними

якщо вiдповiднi iм напрямленi вiдрiзки паралельнi однiй площинi або лежать в однiй площинi.

Очевидно, що коли компланарнi вектори ,, вiдкласти вiд довiльноi точки O (=, =,=), то точки О, А, В, С лежатимуть в однiй площинi (мал. 14).

Отже, якщо вектори компланарнi, то iснують такi iх представники, якi лежать в однiй площинi.

Очевидно, що якщо серед трьох векторiв i два колiнеарних, то цi вектори компанарнi. РЖ навпаки, якщо три вектори некомпланарнi, то серед них немаi колiнеарних.

Теорема 1. (про розклад вектора за двома не колiнеарними векторами). Якщо вектори ,,компланарнi, а вектори ,неколiнеарнi, то iснують iдинi числа α, βтакi, що: = α + β. /2/

РЖнакше кажучи, вектор можна розкласти за векторами i i до того ж iдиним способом.

Доведення. Доведемо спочатку iснування чисел α i β, що задовольняють рiвнiсть /2/. Вiдкладемо вiд деякоi точки O вектори =, =, =. Оскiльки цi вектори компланарнi, то точки О, А, В, С лежать в однiй площинi. Вектори i неколiнеарнi, тому O,A, Bне лежать на однiй прямiй.

Можливi два випадки:

1. Точка С належить прямiй ОВ (мал. 15a). Тодi вектори i колiнеарнi i, отже, за попередньою теоремою, = β, де β тАУ деяке число. Отже, =0*+ β, тобто маi мiсце розклад /2/.

2. С (ОВ). Проведемо || OB (мал. 15b). Тодi за правилом трикутника =+. Але ця рiвнiсть можлива тiльки тодi, коли α =, β =. Дiйсно, якби, наприклад, α , то було б, ||, що суперечить умовi теореми. Отже, припущення неправильне. Тому iснуi iдиний розклад вектора за векторами i . Теорему доведено.

Теорема 2. (про розклад вектора за трьома некомпланарними векторами). Якщо вектори , , некомпланарнi, то для будь-якого вектора , iснують i притому iдинi числа α, β, γ такi, що = α+β+γ .

Лiнiйна залежнiсть векторiв

Означення. Система векторiв називаiться лiнiйно залежною, якщо iснують такi числа , ,тАж, серед яких хоча б одне вiдмiнне вiд нуля, що ++ тАж += 0. / 4/

Якщо ж рiвнiсть /4/ справджуiться тiльки при ==тАж== 0, то дана система векторiв називаiться лiнiйно незалежною.

Сума ++ тАж + називаiться лiнiйною комбiнацiiю векторiв .

Розглянемо деякi властивостi лiнiйноi залежностi векторiв, якi будуть потрiбнi надалi.

Властивiсть 1. Система векторiв лiнiйно залежна тодi i тiльки тодi, коли хоча б один з векторiв i лiнiйною комбiнацiiю iнших векторiв цiii системи.

Доведення.

1. Необхiднiсть. Нехай система векторiв лiнiйно залежна. Тодi iснують такi числа , ,тАж, , що ++ тАж += 0 /5/

При цьому принаймнi одне з чисел , ,тАж, не дорiвнюi нулю. Нехай, нап

Вместе с этим смотрят:

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов