Решение параболических уравнений
К дифференциальным уравнениям с частными производными приходим при решении самых разнообразных задач. Например, при помощи дифференциальных уравнений с частными производными можно решать задачи теплопроводности, диффузии, многих физических и химических процессов.
Как правило, найти точное решение этих уравнений не удается, поэтому наиболее широкое применение получили приближенные методы их решения. В данной работе ограничимся рассмотрением дифференциальных уравнений с частными производными второго порядка, а точнее дифференциальными уравнениями с частными производными второго порядка параболического типа, когда эти уравнения являются линейными, а искомая функция зависит от двух переменных. В общем случае такое уравнение записывается следующим образом:
.
Заметим, что численными методами приходится решать и нелинейные уравнения, но находить их решение много труднее, чем решение линейных уравнений.
введем в рассмотрение величину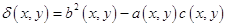 
. В том случае, когда 
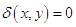уравнение называется параболическим. В случае, когда величина 
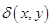не сохраняет знак, имеем смешанный тип дифференциального уравнения. Следует отметить, что в дифференциальном уравнении все функции 
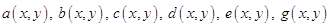являются известными, и они определены в области 
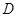, в которой мы ищем решение.
1. Теоретическая часть
1.1 Метод сеток решения уравнений параболического типа
Для решения дифференциальных уравнений параболического типа существует несколько методов их численного решения на ЭВМ, однако особое положение занимает метод сеток, так как он обеспечивает наилучшие соотношения скорости, точности полученного решения и простоты реализации вычислительного алгоритма. Метод сеток еще называют методом конечных разностей. Пусть дано дифференциальное уравнение
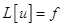. (1.1)
Требуется найти функцию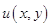 
в области 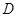с границей 
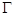при заданных краевых условиях. Согласно методу сеток в плоской области 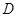строится сеточная область 
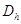, состоящая из одинаковых ячеек. При этом область 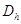должна как можно лучше приближать область 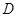. Сеточная область (то есть сетка) 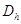состоит из изолированных точек, которые называются узлами сетки. Число узлов будет характеризоваться основными размерами сетки 
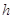: чем меньше 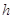, тем больше узлов содержит сетка. Узел сетки называется внутренним, если он принадлежит области 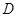, а все соседние узлы принадлежат сетке 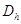. В противном случае он называется граничным. Совокупность граничных узлов образует границу сеточной области 
.
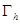Сетка может состоять из клеток разной конфигурации: квадратных, прямоугольных, треугольных и других. После построения сетки исходное дифференциальное уравнение заменяется разностным уравнением во всех внутренних узлах сетки. Затем на основании граничных условий устанавливаются значения искомого решения в граничных узлах. Присоединяя граничные условия сеточной задачи к разностным уравнениям, записанных для внутренних узлов, получаем систему уравнений, из которой определяем значения искомого решения во всех узлах сетки.
Замена дифференциального уравнения разностным может быть осуществлена разными способами. Один из способов аппроксимации состоит в том, что производные, входящие в дифференциальное уравнение, заменяются линейными комбинациями значений функции 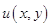в узлах сетки по тем или иным формулам численного дифференцирования. Различные формулы численного дифференцирования имеют разную точность, поэтому от выбора формул аппроксимации зависит качество аппроксимации дифференциального уравнения разностным уравнением.
Рассмотрим неоднородное уравнение теплопроводности, являющееся частным случаем уравнений параболического типа:
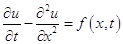, (1.2)
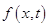тАУ известная функция.
Будем искать решение этого уравнения в области
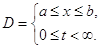
Заметим, что эту полуполосу всегда можно привести к полуполосе, когда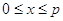 
. Уравнение (1.2) будем решать с начальными условиями:
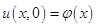, (1.3)
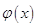тАУ известная функция, и краевыми условиями:
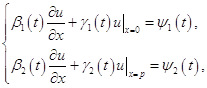(1.4)
где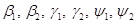 
тАУ известные функции переменной 
.
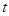Для решения задачи область 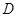покроем сеткой 
.
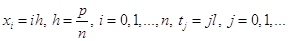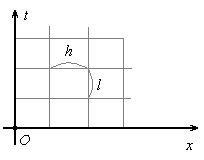
Узлы сетки, лежащие на прямых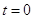 
, 
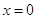и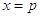 
будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной 
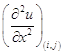воспользуемся следующей формулой:
.
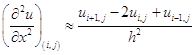Для производной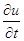 
запишем следующие формулы:
,
,
.
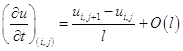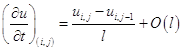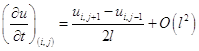Можем получить три вида разностных уравнений:
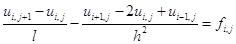, (1.5)
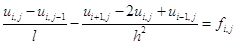, (1.6)
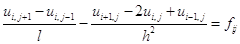, (1.7)
.
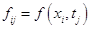Разностные уравнения (1.5) аппроксимируют уравнение (1.2) с погрешностью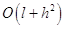 
, уравнение (1.6) тАУ с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью 
.
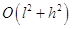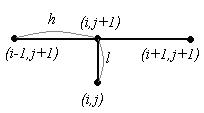
В разностной схеме (1.5) задействованы 4 узла. Конфигурация схемы (1.5) имеет вид:
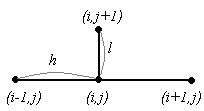
В схеме (1.6) также участвуют 4 узла, и эта схема имеет вид:
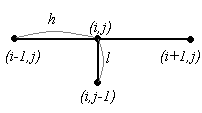
В схеме (1.7) участвуют 5 узлов, и эта схема имеет вид:
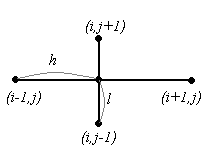
Первая и третья схемы тАУ явные, вторая схема неявная. В случае явных схем значения функции в узле очередного слоя можно найти, зная значения в узлах предыдущих слоев. В случае неявных схем для нахождения значений решения в узлах очередного слоя приходится решать систему уравнений.
Для узлов начального (нулевого) слоя 
значения решения выписываются с помощью начального условия (1.3):
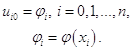(1.8)
Для граничных узлов, лежащих на прямых 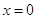и 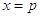, заменив производные 
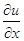по формулам численного дифференцирования, получаем из граничных условий (1.4) следующие уравнения:
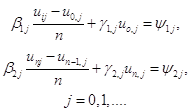(1.9)
Уравнения (1.9) аппроксимируют граничные условия (1.4) с погрешностью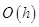 
, так как используем односторонние формулы численного дифференцирования. Погрешность аппроксимации можно понизить, если использовать более точные односторонние (с тремя узлами) формулы численного дифференцирования.
Присоединяя к системе разностных уравнений, записанных для внутренних узлов, начальные и граничные условия (1.8) и (1.9) для разностной задачи получим полные разностные схемы трех видов. Для проведения вычислений самой простой схемой оказывается первая: достаточно на основании начального условия найти значения функции в узлах слоя 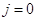, чтобы в дальнейшем последовательно определять значения решения в узлах слоев 
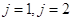и т.д.
Третья схема также весьма проста для проведения вычислений, но при ее использовании необходимо кроме значений решения в узлах слоя 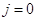найти каким-то образом значения функции и в слое 
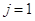. Далее вычислительный процесс легко организовывается. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи.
С точки зрения точечной аппроксимации третья схема самая точная.
Введем в рассмотрение параметр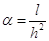 
. Тогда наши разностные схемы можно переписать, вводя указанный параметр. При этом самый простой их вид будет при 
.
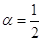В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.
Разрешимость этой системы для явных схем вопросов не вызывает, так как все действия выполняются в явно определенной последовательности. В случае неявных схем разрешимость системы следует исследовать в каждом конкретном случае. Важным вопросом является вопрос о том, на сколько найденные решения хорошо (адекватно) отражают точные решения, и можно ли неограниченно сгущая сетку (уменьшая шаг по осям) получить приближенные решения, сколь угодно близкие к точным решениям? Это вопрос о сходимости метода сеток.
На практике следует применять сходящиеся разностные схемы, причем только те из них, которые являются устойчивыми, то есть при использовании которых небольшие ошибки в начальных или промежуточных результатах не приводят к большим отклонениям от точного решения. Всегда следует использовать устойчивые разностные схемы, проводя соответствующие исследования на устойчивость.
Первая из построенных выше разностных схем в случае первой краевой задачи будет устойчивой при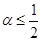 
. Вторая схема устойчива при всех значениях величины 
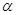. Третья схема неустойчива для любых 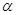, что сводит на нет все ее преимущества и делает невозможной к применению на ЭВМ.
Явные схемы просты для организации вычислительного процесса, но имеют один весьма весомый недостаток: для их устойчивости приходится накладывать сильные ограничения на сетку. Неявные схемы свободны от этого недостатка, но есть другая трудность тАУ надо решать системы уравнений большой размерности, что на практике при нахождении решения сложных уравнений в протяженной области с высокой степенью точности может потребовать больших объемов памяти ЭВМ и времени на ожидание конечного результата. К счастью, прогресс не стоит на месте и уже сейчас мощности современных ЭВМ вполне достаточно для решения поставленных перед ними задач.
1.2 Метод прогонки решения разностной задачи для уравнений параболического типа
Рассмотрим частный случай задачи, поставленной в предыдущем разделе. В области
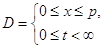
найти решение уравнения
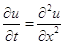(1.10)
с граничными условиями
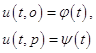(1.11)
и начальным условием
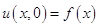. (1.12)
Рассмотрим устойчивую вычислительную схему, для которой величина 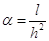не является ограниченной сверху, а, значит, шаг по ос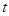и и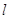 
может быть выбран достаточно крупным. Покроем область 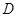сеткой
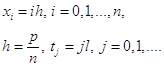
Запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (1.10) во всех внутренних узлах слоя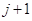 
. При этом будем использовать следующие формулы:
,
.
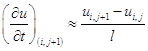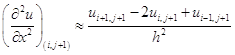Эти формулы имеет погрешность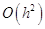 
. В результате уравнение (1.10) заменяется разностным:
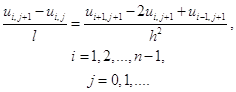(1.13)
Перепишем (1.13) в виде:
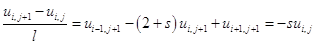. (1.14)
Данная вычислительная схема имеет следующую конфигурацию:
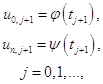(1.15)
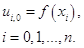(1.16)
Система (1.14) тАУ (1.16) представляет собой разностную задачу, соответствующую краевой задаче (1.10) тАУ (1.12).
За величину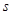 
мы положили 
.
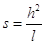(1.14) тАУ (1.16) есть система линейных алгебраических уравнений с 3-диагональной матрицей, поэтому ее резонно решать методом прогонки, так как он в несколько раз превосходит по скорости метод Гаусса.
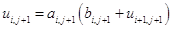. (1.17)
Здесь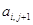 
, 
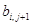тАУ некоторые коэффициенты, подлежащие определению. Заменив в (1.17) 
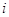на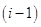 
будем иметь:
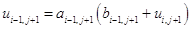. (1.18)
Подставив уравнение (1.18) в (1.14) получим:
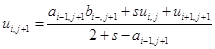. (1.19)
Сравнив (1.17) и (1.19) найдем, что:
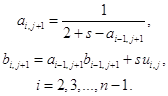(1.20)
Положим в (1.14)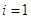 
и найдем из него 
:
,
.
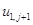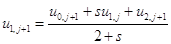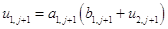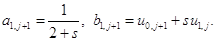(1.21)
Заметим, что во второй формуле (1.21) величина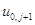 
подлежит замене на 
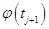согласно первому условию (1.15).
С помощью формул (1.21) и (1.20) проводим прогонку в прямом направлении. В результате находим величины
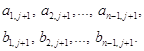
Затем осуществляем обратный ход. При этом воспользуемся второй из формул (1.15) и формулой (1.17). Получим следующую цепочку формул:
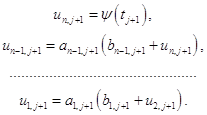(1.22)
Таким образом, отправляясь от начального слоя 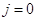, на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки.
Итак, мы построили неявную схему решения дифференциальных уравнений параболического типа методом сеток.
1.3 Оценка погрешности и сходимость метода сеток
При решении задачи методом сеток мы допускаем погрешность, состоящую из погрешности метода и вычислительной погрешности.
Погрешность метода тАУ это та погрешность, которая возникает в результате замены дифференциального уравнения разностным, а также погрешность, возникающая за счет сноса граничных условий с 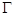на .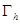
Вычислительная погрешность тАУ это погрешность, возникающая при решении системы разностных уравнений, за счет практически неизбежных машинных округлений.
Существуют специальные оценки погрешности для решения задач методом сеток. Однако эти оценки содержат максимумы модулей производных искомого решения, поэтому пользоваться ими крайне неудобно, однако эти теоретические оценки хороши тем, что из них видно: если неограниченно измельчать сетку, то последовательность решений будет сходиться равномерно к точному решению. Здесь мы столкнулись с проблемой сходимости метода сеток. При использовании метода сеток мы должны быть уверены, что, неограниченно сгущая сетку, можем получить решение, сколь угодно близкое к точному.
Итак, на примере решения краевой задачи для дифференциального уравнения параболического типа рассмотрим основные принципы метода сеток. Отметим, что если при решении разностной задачи небольшие ошибки в начальных и краевых условиях (или в промежуточных результатах) не могут привести к большим отклонениям искомого решения, то говорят, что задача поставлена корректно в смысле устойчивости по входным данным. Разностную схему называют устойчивой, если вычислительная погрешность неограниченно не возрастает. В противном случае схема называется неустойчивой.
1.4 Доказательство устойчивости разностной схемы
Пусть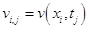 
есть решение уравнения (1.14), удовлетворяющее возмущенным начальным условиям
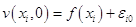
и граничным условиям
.
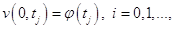
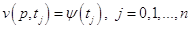Здесь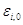 
тАУ некоторые начальные ошибки.
Рассмотрим погрешность
.
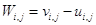Погрешность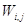 
будет удовлетворять уравнению
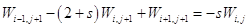(1.23)
(в силу линейности уравнения (1.14)), а также следующими граничными и начальными условиями:
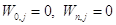, (1.24)
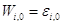. (1.25)
Частное решение уравнения (1.23) будем искать в виде
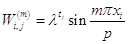. (1.26)
Здесь числа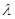 
и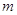 
следует подобрать так, чтобы выражение (1.26) удовлетворяло уравнению (1.23) и граничным условиям (1.24).
При целом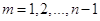 
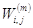удовлетворяет уравнению (1.23) и условиям (1.24).
Подставим уравнение (1.26) в уравнение (1.24). При этом получим:
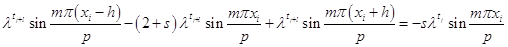
или
.
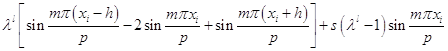Выражение в квадратных скобках равно
.
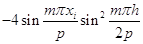Подставляя это выражение в предыдущее уравнение вместо выражения в квадратных скобках и проводя сокращения на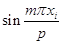 
получим:
,
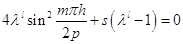откуда находим :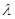
.
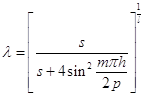Таким образом, согласно уравнению (1.26), получаем линейно-независимые решения уравнения (1.23) в виде
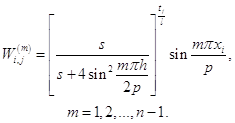
Заметим, что это частное решение удовлетворяет однородным краевым условиям (1.24). Линейная комбинация этих частных решений также является решением уравнения (1.23):
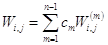, (1.27)
причем 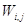, определенное в выражении (1.27), удовлетворяет для любых 
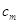однородным граничным условиям (1.24). Коэффициенты 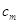подбираются исходя из того, что 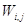должны удовлетворять начальным условиям (1.25):
.
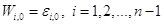В результате получаем систему уравнений
,
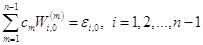содержащую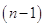 
уравнений с 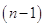неизвестными 
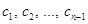. Решая построенную систему определяем неизвестные коэффициенты .
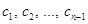Для устойчивости исследуемой разностной схемы необходимо, чтобы при любых значениях коэффициентов 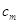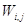, определяемое формулой (1.27), оставалось ограниченной величиной при 
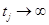. Для этого достаточно, чтобы для всех 
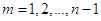выполнялось неравенство
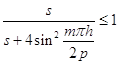. (1.28)
Анализируя (1.28) видим, что это неравенство выполняется для любых значений параметра 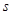. При этом при 
или в крайнем случае, когда
,
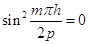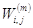остается ограниченным и при фиксированном 
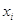не возрастает по модулю. Следовательно мы доказали, что рассматриваемая разностная схема устойчива для любых значений параметра .
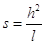2. Реализация метода
2.1 Разработка программного модуля
Поставлена цель: разработать программный продукт для нахождения приближенного решения параболического уравнения:
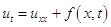(1.29)
в области
,
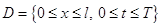удовлетворяющее условиям
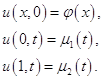(1.30)
Разобьем область 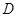прямыми
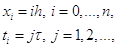
где
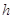тАУ шаг по оси 
,
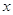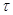тАУ шаг по оси .
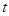Заменив в каждом узле производные конечно-разностными отношениями по неявной схеме, получим систему вида:
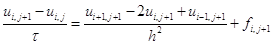. (1.31)
Преобразовав ее, получим:
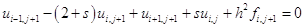, (1.32)
где
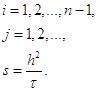
В граничных узлах
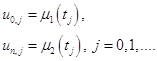(1.33)
В начальный момент
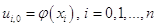. (1.34)
Эта разностная схема устойчива при любом 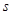. Будем решать систему уравнений (1.32), (1.33) и (1.34) методом прогонки. Для этого ищем значения функции в узле 
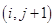в виде
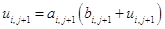, (1.35)
где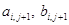 
тАУ пока неизвестные коэффициенты.
Аналогично
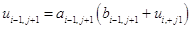. (1.36)
Подставив значение (1.35) в (1.32) получим:
.
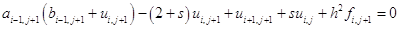Откуда
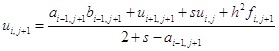. (1.37)
Из сравнения (1.35) и (1.37) видно, что
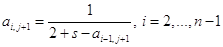. (1.38)
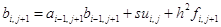. (1.39)
Для 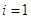из (1.32) имеем:
.
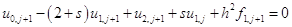Откуда
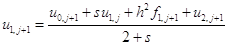
или
.
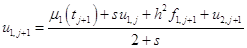Откуда, используя (1.35), получим:
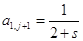, (1.40)
. (1.41)
Используя данный метод, мы все вычисления проведем в следующем порядке для всех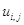 
.
1) Зная значения функции 
на границе (1.33), найдем значения коэффициентов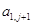 
по (1.40) и 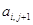по (1.38) для всех 
.
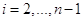2) Найдем 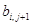по (1.41), используя для 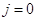начальное условие (1.34).
3) Найдем 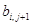по формулам (1.39) для .
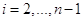4) Найдем значения искомой функции на 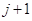слое, начиная с 
:
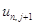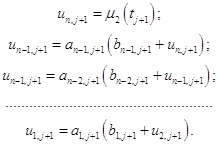
2.2 Описание логики программного модуля
Листинг программы приведен в приложении 1. Ниже будут описаны функции программного модуля и их назначение.
Функция main() является базовой. Она реализует алгоритм метода сеток, описанного в предыдущих разделах работы.
Функция f (x, y) представляет собой свободную функцию двух переменных дифференциального уравнения (1.29). В качестве аргумента в нее передаются два вещественных числа с плавающей точкой типа float. На выходе функция возвращает значение функции 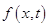, вычисленное в точке 
.
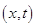Функции mu_1 (t) и mu_2 (t) представляют собой краевые условия. В них передается по одному аргументу (t) вещественного типа (float).
Функция phi() является ответственной за начальный условия.
В функции main() определены следующие константы:
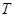тАУ правая граница по 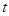для области ;
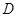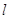тАУ правая граница по 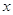для области ;
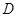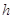тАУ шаг сетки по оси ;
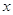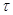тАУ шаг сетки по оси ;
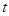Варьируя 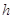и 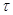можно изменять точность полученного решения 
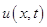от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров 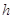и 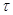, поэтому при устремлении их к нуля можем получить сколь угодно близкое к точному решение.
Программа снабжена тремя механизмами вывода результатов работы: на экран в виде таблицы, в текстовый файл, а также в файл списка математического пакета Waterloo Maple. Это позволяет наглядно представить полученное решение.
Программа написана на языке программирования высокого уровня Borland C++ 3.1 в виде приложения MS-DOS. Обеспечивается полная совместимость программы со всеми широко известными операционными системами корпорации Майкрософт: MS-DOS 5.x, 6.xx, 7.xx, 8.xx, Windows 9x/Me/2000/NT/XP.
2.3 Пример работы программы
В качестве примера рассмотрим численное решение следующего дифференциального уравнения параболического типа:
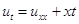
в области
,
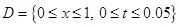удовлетворяющее условиям
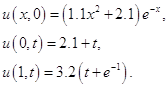
Задав прямоугольную сетку с шагом оси 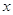0.1 и по оси 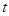0.01, получим следующее решение:
2.10 1.91 1.76 1.63 1.53 1.44 1.37 1.31 1.26 1.22 1.18
2.11 1.75 1.23 1.20 1.15 1.10 1.07 1.04 1.04 1.07 1.21
2.12 1.61 0.95 0.96 0.93 0.91 0.90 0.90 0.94 1.03 1.24
2.13 1.51 0.79 0.81 0.81 0.80 0.81 0.83 0.89 1.03 1.27
2.14 1.45 0.69 0.73 0.74 0.74 0.76 0.80 0.88 1.04 1.31
2.15 1.41 0.64 0.69 0.70 0.71 0.74 0.79 0.89 1.05 1.34
В таблице ось x расположена горизонтально, а ось t расположена вертикально и направлена вниз.
На выполнение программы на среднестатистическом персональном компьютере тратится время, равное нескольким миллисекундам, что говорит о высокой скорости алгоритма.
Подробно выходной файл output.txt, содержащий таблицу значений функции 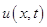представлен в приложении 3.
Заключение
В работе был рассмотрен метод сеток решения параболических уравнений в частных производных. Раскрыты основные понятия метода, аппроксимация уравнения и граничных условий, исследована разрешимость и сходимость получаемой системы разностных уравнений.
На основании изученного теоретического материала была разработана программная реализация метода сеток, проанализирована ее сходимость и быстродействие, проведен тестовый расчет, построен графики полученного численного решения.
Список источников
1. Березин И.С., Жидков Н.П. Методы вычислений. Т.2. тАУ М.: Физматгиз, 1962.
2. Тихонов А.Н., Самарский А.А. Уравнения математической физики. тАУ М.: Наука, 1972.
3. Пирумов У.Г. Численные методы. тАУ М.: Издательство МАИ, 1998.
4. Калиткин Н.Н. Численные методы. тАУ М.: Наука, 1976.
Приложение
Текст программы
// тАУ //
#include
#include
#include
void main(void);
float f (float x, float t);
float mu_1 (float t);
float mu_2 (float t);
float phi (float x);
// тАУ //
void main(void)
{
clrscr();
FILE *myfile;
FILE *plotter;
float a[120] [120];
float b[120] [120];
float u[120] [120];
float T = 0.05;
float l = 1;
float h = 0.1;
float tau = 0.01;
int n, i, j, k;
float s = pow (h, 2) / tau;
n = ceil (l / h);
for (i = 0; i <= 119; i++)
{
for (j = 1; j <= 119; j++)
{
u[i] [j] = 0;
a[i] [j] = 0;
b[i] [j] = 0;
}
}
for (i = 0; i <= n; i++)
{
u[i] [0] = phi (i * h);
}
for (j = 0; j <= floor (T /tau); j++)
{
u[0] [j] = mu_1 (tau * j);
u[n] [j] = mu_2 (tau * j);
}
for (j = 0; j <= floor (T / tau); j++)
{
a[1] [j + 1] = 1 / (2 + s);
for (i = 2; i <= n тАУ 1; i++)
{
a[i] [j + 1] = 1 / (2 + s тАУ a [i тАУ 1] [j + 1]);
}
b[1] [j + 1] = mu_1 ((j + 1) * tau) + s * u[1] [j] + pow (h, 2) * f (h, (j + 1) * tau);
for (i = 2; i <= n тАУ 1; i++)
{
b[i] [j + 1] = a [i тАУ 1] [j + 1] + s * u[i] [j] + pow (h, 2) * f (i * h, (j + 1) * tau);
}
u[n] [j + 1] = mu_2 ((j + 1) * tau);
for (k = 1; k <= n тАУ 1; k++)
{
u [n тАУ k] [j + 1] = a [n тАУ k] [j + 1] * (b [n тАУ k] [j + 1] + u [n тАУ k + 1] [j + 1]);
}
}
myfile = fopen (Влoutput.txtВ», Влw+В»);
plotter = fopen (Вл3dplot.txtВ», Влw+В»);
fprintf (myfile, ВлТаблица значений функции u=u (x, t) в области D={0<=X<=%g, 0<=T<=%g}:\nВ», l, T);
printf (ВлЗначения функции u (x, t) в области D={0<=X<=%g, 0<=T<=%g}:\n\nВ», l, T);
for (j = 0; j <= floor (T / tau); j++)
{
for (i = 0; i <= n; i++)
{
printf (Вл%.2fВ», u[i] [j]);
fprintf (myfile, Влu(%g) (%g)=%g;\nВ», i * h, j * tau, u[i] [j]);
if (i < n && j < floor (T / tau))
{
fprintf (plotter, Вл[[%g, %g, %g], [%g, %g, %g], [%g, %g, %g], [%g, %g, %g]]В», i * h, j * tau, u[i] [j], (i + 1) * h, j * tau, u [i + 1] [j], i * h, (j + 1) * tau, u[i] [j + 1], (i + 1) * h, (j + 1) * tau, u [i + 1] [j + 1]);
if (i >= n тАУ 1 && j >= floor (T / tau) тАУ 1)
{
}
else
{
fprintf (plotter,В»,В»);
}
}
}
printf (Вл\nВ»);
}
fclose(myfile);
fclose(plotter);
printf (Вл\nОсь x расположена горизонтально; ось t расположена вертикально и направлена внизВ»);
printf (ВлШаг по оси x равен % g; шаг по оси t равен % g.\nВ», h, tau);
printf (Вл\nДля выхода нажмите ENTERтАжВ»);
while (getch()!= 13);
}
// тАУ //
float f (float x, float t)
{
return x * t;
}
// тАУ //
float mu_1 (float t)
{
return 2.1 + t;
}
// тАУ //
float mu_2 (float t)
{
return 3.2 * (t + 1 / 2.71828);
}
// тАУ //
float phi (float x)
{
return (1.1 * pow (x, 2) + 2.1) * exp(-x);
}
Вместе с этим смотрят:
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов