Система массового обслуживания с ограниченным временем ожидания
Федеральное агентство по образованию РФ
ФГОУ СПО ВлПеревозский строительный колледжВ»
Курсовая работа
по дисциплине ВлМатематические методыВ»
на тему ВлСМО с ограниченным временем ожидания. Замкнутые СМОВ»
Перевоз
2008
Содержание
Введение..................................................... 2
1. Основы теории массового обслуживания......................... 3
1.1 Понятие случайного процесса................................. 3
1.2 Марковский случайный процесс............................... 4
1.3 Потоки событий............................................. 6
1.4 Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний..................................................... 9
1.5 Задачи теории массового обслуживания........................ 13
1.6 Классификация систем массового обслуживания................. 15
2. Системы массового обслуживания с ожиданием................... 16
2.1 Одноканальная СМО с ожиданием............................ 16
2.2 Многоканальная СМО с ожиданием........................... 25
3. Замкнутые СМО............................................ 37
Решение задачи............................................... 45
Заключение.................................................. 50
Список литературы............................................ 51
Введение
В данном курсе мы будем рассматривать различные системы массового обслуживания (СМО) и сети массового обслуживания (СеМО).
Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного обслуживания потока заявок (требований на обслуживание) при ограничениях на ресурсы системы.
Модели СМО удобны для описания отдельных подсистем современных вычислительных систем, таких как подсистема процессор - основная память, канал ввода-вывода и т. д. Вычислительная система в целом представляет собой совокупность взаимосвязанных подсистем, взаимодействие которых носит вероятностный характер. Заявка на решение некоторой задачи, поступающая в вычислительную систему, проходит последовательность этапов счета, обращения к внешним запоминающим устройствам и устройствам ввода-вывода. После выполнения некоторой последовательности таких этапов, число и продолжительность которых зависит от трудоемкости программы, заявка считается обслуженной и покидает вычислительную систему. Таким образом, вычислительную систему в целом можно представлять совокупностью СМО, каждая из которых отображает процесс функционирования отдельного устройства или группы однотипных устройств, входящих в состав системы.
Совокупность взаимосвязанных СМО называется сетью массового обслуживания (стохастической сетью).
Для начала мы рассмотрим основы теории СМО, затем перейдем к ознакомлению в подробном содержании к СМО с ожиданием и замкнутым СМО. Также в курс включена практическая часть, в которой мы подробно познакомимся с тем, как применить теорию на практике.
1. Основы теории массового обслуживания
Теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваются вероятностные задачи и математические модели (до этого нами рассматривались детерминированные математические модели). Напомним, что:
Детерминированная математическая модель отражает поведение объекта (системы, процесса) с позиций полной определенности в настоящем и будущем.
Вероятностная математическая модель учитывает влияние случайных факторов на поведение объекта (системы, процесса) и, следовательно, оценивает будущее с позиций вероятности тех или иных событий.
Т.е. здесь как, например, в теории игр задачи рассматриваются в условияхнеопределенности.
Рассмотрим сначала некоторые понятия, которые характеризуют Влстохастическую неопределенностьВ», когда неопределенные факторы, входящие в задачу, представляют собой случайные величины (или случайные функции), вероятностные характеристики которых либо известны, либо могут быть получены из опыта. Такую неопределенность называют еще ВлблагоприятнойВ», ВлдоброкачественнойВ».
1.1 Понятие случайного процесса
Строго говоря, случайные возмущения присущи любому процессу. Проще привести примеры случайного, чем ВлнеслучайногоВ» процесса. Даже, например, процесс хода часов (вроде бы это строгая выверенная работа тАУ Влработает как часыВ») подвержен случайным изменениям (уход вперед, отставание, остановка). Но до тех пор, пока эти возмущения несущественны, мало влияют на интересующие нас параметры, мы можем ими пренебречь и рассматривать процесс как детерминированный, неслучайный.
Пусть имеется некоторая система S (техническое устройство, группа таких устройств, технологическая система тАУ станок, участок, цех, предприятие, отрасль промышленности и т.д.). В системе S протекает случайный процесс, если она с течением времени меняет свое состояние (переходит из одного состояния в другое), причем, заранее неизвестным случайным образом.
Примеры:
1. Система S тАУ технологическая система (участок станков). Станки время от времени выходят из строя и ремонтируются. Процесс, протекающий в этой системе, случаен.
2. Система S тАУ самолет, совершающий рейс на заданной высоте по определенному маршруту. Возмущающие факторы тАУ метеоусловия, ошибки экипажа и т.д., последствия тАУ ВлболтанкаВ», нарушение графика полетов и т.д.
1.2 Марковский случайный процесс
Случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.
Пусть в настоящий момент t0 система находится в определенном состоянии S0. Мы знаем характеристики состояния системы в настоящем 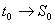 и все, что было при t<t0 (предысторию процесса). Можем ли мы предугадать (предсказать) будущее, т.е. что будет при t>t0? В точности тАУ нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время
и все, что было при t<t0 (предысторию процесса). Можем ли мы предугадать (предсказать) будущее, т.е. что будет при t>t0? В точности тАУ нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время 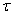 система S окажется в состоянии S1 или останется в состоянии S0 и т.д.
система S окажется в состоянии S1 или останется в состоянии S0 и т.д.
Пример. Система S тАУ группа самолетов, участвующих в воздушном бою. Пусть x тАУ количество ВлкрасныхВ» самолетов, y тАУ количество ВлсинихВ» самолетов. К моменту времени t0 количество сохранившихся (не сбитых) самолетов соответственно тАУ x0, y0. Нас интересует вероятность того, что в момент времени 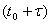 численный перевес будет на стороне ВлкрасныхВ». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t0, а не от того, когда и в какой последовательности погибали сбитые до момента t0 самолеты.
численный перевес будет на стороне ВлкрасныхВ». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t0, а не от того, когда и в какой последовательности погибали сбитые до момента t0 самолеты.
На практике Марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием ВлпредысторииВ» можно пренебречь. И при изучении таких процессов можно применять Марковские модели (в теории массового обслуживания рассматриваются и не Марковские системы массового обслуживания, но математический аппарат, их описывающий, гораздо сложнее).
В исследовании операций большое значение имеют Марковские случайные процессы с дискретными состояниями и непрерывным временем.
Процесс называется процессом с дискретным состоянием, если его возможные состояния S1, S2, тАж можно заранее определить, и переход системы из состояния в состояние происходит ВлскачкомВ», практически мгновенно.
Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны и могут произойти в любой момент.
Далее рассматриваются только процессы с дискретным состоянием и непрерывным временем.
Пример. Технологическая система (участок) S состоит из двух станков, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время. Возможны следующие состояния системы:
S0 - оба станка исправны;
S1 - первый станок ремонтируется, второй исправен;
S2 - второй станок ремонтируется, первый исправен;
S3 - оба станка ремонтируются.
Переходы системы S из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или иного станка или окончания ремонта.
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой тАУ графом состояний. Вершины графа тАУ состояния системы. Дуги графа тАУ возможные переходы из состояния в состояние. Для нашего примера граф состояний приведен на рис. 1.
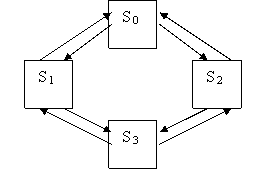
Рис. 1. Граф состояний системы
Примечание. Переход из состояния S0 в S3 на рисунке не обозначен, т.к. предполагается, что станки выходят из строя независимо друг от друга. Вероятностью одновременного выхода из строя обоих станков мы пренебрегаем.
1.3 Потоки событий
Поток событий тАУ последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
В предыдущем примере тАУ это поток отказов и поток восстановлений. Другие примеры: поток вызовов на телефонной станции, поток покупателей в магазине и т.д.
Поток событий можно наглядно изобразить рядом точек на оси времени Ot тАУ рис. 2.
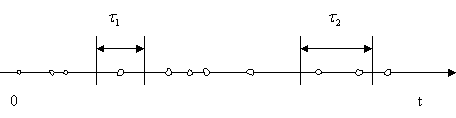
Рис. 2. Изображение потока событий на оси времени
Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.
Интенсивность потока событий (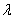 ) тАУ это среднее число событий, приходящееся на единицу времени.
) тАУ это среднее число событий, приходящееся на единицу времени.
Рассмотрим некоторые свойства (виды) потоков событий.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.
В частности, интенсивность 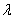 стационарного потока постоянна. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
стационарного потока постоянна. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени 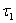 и
и 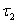 (см. рис. 2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.
(см. рис. 2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами:
1) стационарен;
2) ординарен;
3) не имеет последствий.
Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.
Для простейшего потока с интенсивностью 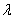 интервал T между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью:
интервал T между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью:
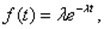
где 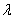 - параметр показательного закона.
- параметр показательного закона.
Для случайной величины T, имеющей показательное распределение, математическое ожидание 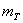 есть величина, обратная параметру, а среднее квадратичное отклонение
есть величина, обратная параметру, а среднее квадратичное отклонение 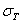 равно математическому ожиданию:
равно математическому ожиданию:
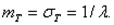
1.4 Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний
Рассматривая Марковские процессы с дискретными состояниями и непрерывным временем, подразумевается, что все переходы системы S из состояния в состояние происходят под действием простейших потоков событий (потоков вызовов, потоков отказов, потоков восстановлений и т.д.). Если все потоки событий, переводящие систему S из состояния в состояние простейшие, то процесс, протекающий в системе, будет Марковским.
Итак, на систему, находящуюся в состоянии 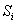 , действует простейший поток событий. Как только появится первое событие этого потока, происходит ВлперескокВ» системы из состояния
, действует простейший поток событий. Как только появится первое событие этого потока, происходит ВлперескокВ» системы из состояния 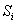 в состояние
в состояние 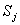 (на графе состояний по стрелке
(на графе состояний по стрелке 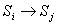 ).
).
Для наглядности на графе состояний системы у каждой дуги проставляют интенсивности того потока событий, который переводит систему по данной дуге (стрелке). 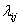 - интенсивность потока событий, переводящий систему из состояния
- интенсивность потока событий, переводящий систему из состояния  в
в  . Такой граф называется размеченным. Для нашего примера размеченный граф приведен на рис. 3.
. Такой граф называется размеченным. Для нашего примера размеченный граф приведен на рис. 3.
Рис. 3. Размеченный граф состояний системы
На этом рисунке  - интенсивности потока отказов;
- интенсивности потока отказов; 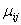 - интенсивности потока восстановлений.
- интенсивности потока восстановлений.
Предполагаем, что среднее время ремонта станка не зависит от того, ремонтируется ли один станок или оба сразу. Т.е. ремонтом каждого станка занят отдельный специалист.
Пусть система находится в состоянии S0. В состояние S1 ее переводит поток отказов первого станка. Его интенсивность равна:
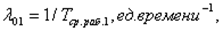
где 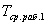 - среднее время безотказной работы первого станка.
- среднее время безотказной работы первого станка.
Из состояния S1 в S0 систему переводит поток Влокончаний ремонтовВ» первого станка. Его интенсивность равна:
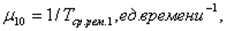
где 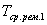 - среднее время ремонта первого станка.
- среднее время ремонта первого станка.
Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем дугам графа. Имея в своем распоряжении размеченный граф состояний системы, строится математическая модель данного процесса.
Пусть рассматриваемая система S имеет 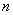 -возможных состояний
-возможных состояний 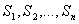 . Вероятность
. Вероятность 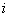 -го состояния
-го состояния 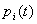 - это вероятность того, что в момент времени
- это вероятность того, что в момент времени 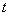 , система будет находиться в состоянии
, система будет находиться в состоянии 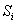 . Очевидно, что для любого момента времени сумма всех вероятностей состояний равна единице:
. Очевидно, что для любого момента времени сумма всех вероятностей состояний равна единице:

Для нахождения всех вероятностей состояний 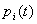 как функций времени составляются и решаются уравнения Колмогорова тАУ особого вида уравнения, в которых неизвестными функциями являются вероятности состояний. Правило составления этих уравнений приведем здесь без доказательств. Но прежде, чем его приводить, объясним понятие финальной вероятности состояния.
как функций времени составляются и решаются уравнения Колмогорова тАУ особого вида уравнения, в которых неизвестными функциями являются вероятности состояний. Правило составления этих уравнений приведем здесь без доказательств. Но прежде, чем его приводить, объясним понятие финальной вероятности состояния.
Что будет происходить с вероятностями состояний при 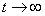 ? Будут ли
? Будут ли 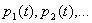 стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний.
стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний.
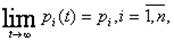
где 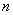 - конечное число состояний системы.
- конечное число состояний системы.
Финальные вероятности состояний тАУ это уже не переменные величины (функции времени), а постоянные числа. Очевидно, что:
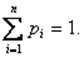
Финальная вероятность состояния 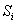 тАУ это потАУсуществу среднее относительное время пребывания системы в этом состоянии.
тАУ это потАУсуществу среднее относительное время пребывания системы в этом состоянии.
Например, система S имеет три состояния S1, S2 и S3. Их финальные вероятности равны соответственно 0,2; 0,3 и 0,5. Это значит, что система в предельном стационарном состоянии в среднем 2/10 времени проводит в состоянии S1, 3/10 тАУ в состоянии S2 и 5/10 тАУ в состоянии S3.
Правило составления системы уравнений Колмогорова: в каждом уравнении системы в левой его части стоит финальная вероятность данного состояния 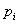 , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а в правой егочасти тАУ сумма произведений интенсивностей всех потоков, входящих в
, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а в правой егочасти тАУ сумма произведений интенсивностей всех потоков, входящих в 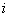 -е состояние, на вероятности тех состояний, из которых эти потоки исходят.
-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пользуясь этим правилом, напишем систему уравнений для нашего примера:
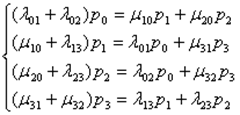 .
.
Эту систему четырех уравнений с четырьмя неизвестными 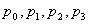 , казалось бы, можно вполне решить. Но эти уравнения однородны (не имеют свободного члена), и, значит, определяют неизвестные только с точностью до произвольного множителя. Однако можно воспользоваться нормировочным условием:
, казалось бы, можно вполне решить. Но эти уравнения однородны (не имеют свободного члена), и, значит, определяют неизвестные только с точностью до произвольного множителя. Однако можно воспользоваться нормировочным условием: 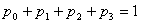 и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
Продолжение примера. Пусть значения интенсивностей потоков равны: 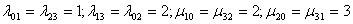 .
.
Четвертое уравнение отбрасываем, добавляя вместо него нормировочное условие:
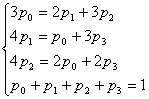 .
.
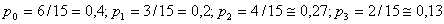 .
.
Т.е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии S0 (оба станка исправны), 20% - в состоянии S1 (первый станок ремонтируется, второй работает), 27% - в состоянии S2 (второй станок ремонтируется, первый работает), 13% - в состоянии S3 (оба станка ремонтируются). Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов.
Пусть система S в состоянии S0 (полностью исправна) приносит в единицу времени доход 8 условных единиц, в состоянии S1 тАУ доход 3 условные единицы, в состоянии S2 тАУ доход 5 условных единиц, в состоянии S3 тАУ не приносит дохода. Тогда в предельном, стационарном режиме средний доход в единицу времени будет равен: 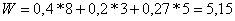 условных единиц.
условных единиц.
Станок 1 ремонтируется долю времени, равную: 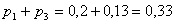 . Станок 2 ремонтируется долю времени, равную:
. Станок 2 ремонтируется долю времени, равную: 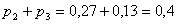 . Возникает задача оптимизации. Пусть мы можем уменьшить среднее время ремонта первого или второго станка (или обоих), но это нам обойдется в определенную сумму. Спрашивается, окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт? Нужно будет решить систему четырех уравнений с четырьмя неизвестными.
. Возникает задача оптимизации. Пусть мы можем уменьшить среднее время ремонта первого или второго станка (или обоих), но это нам обойдется в определенную сумму. Спрашивается, окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт? Нужно будет решить систему четырех уравнений с четырьмя неизвестными.
1.5 Задачи теории массового обслуживания
Примеры систем массового обслуживания (СМО): телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, станочные и другие технологические системы, системы управления гибких производственных систем и т.д.
Каждая СМО состоит из какоготАУто количества обслуживающих единиц, которые называются каналами обслуживания (это станки, транспортные тележки, роботы, линии связи, кассиры, продавцы и т.д.). Всякая СМО предназначена для обслуживания какоготАУто потока заявок (требований), поступающих в какие-то случайные моменты времени.
Обслуживание заявки продолжается какоетАУто, вообще говоря, случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какиетАУто периоды времени на входе СМО скапливается излишне большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными). В другие же периоды СМО будет работать с недогрузкой или вообще простаивать.
Процесс работы СМО тАУ случайный процесс с дискретными состояниями и непрерывным временем. Состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой надоело ждать, покидает очередь).
Предмет теории массового обслуживания тАУ построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками тАУ показателями эффективности СМО. Эти показатели описывают способность СМО справляться с потоком заявок. Ими могут быть: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди; среднее время ожидания обслуживания и т.д.
Математический анализ работы СМО очень облегчается, если процесс этой работы Марковский, т.е. потоки событий, переводящие систему из состояния в состояние тАУ простейшие. Иначе математическое описание процесса очень усложняется и его редко удается довести до конкретных аналитических зависимостей. На практике не Марковские процессы с приближением приводятся к Марковским. Приведенный далее математический аппарат описывает Марковские процессы.
1.6 Классификация систем массового обслуживания
Первое деление (по наличию очередей):
1. СМО с отказами;
2. СМО с очередью.
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем не обслуживается.
В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной.
СМО с очередями подразделяются на разные виды в зависимости от того, как организована очередь тАУ ограничена или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания, Влдисциплины обслуживанияВ».
Итак, например, рассматриваются следующие СМО:
В· СМО с нетерпеливыми заявками (длина очереди и время обслуживания ограничено);
В· СМО с обслуживанием с приоритетом, т.е. некоторые заявки обслуживаются вне очереди и т.д.
Кроме этого СМО делятся на открытые СМО и замкнутые СМО.
В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО тАУ зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока ВлтребованийВ» со стороны станков зависит от того, сколько их уже исправно и ждет наладки.
Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.
2. Системы массового обслуживания с ожиданием
2.1 Одноканальная СМО с ожиданием
Рассмотрим простейшую СМО с ожиданием тАФ одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью 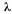 ; интенсивность обслуживания
; интенсивность обслуживания 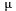 (т.е. в среднем непрерывно занятый канал будет выдавать
(т.е. в среднем непрерывно занятый канал будет выдавать  обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди уже стоят m-заявок, она покидает систему не обслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
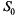 тАФ канал свободен;
тАФ канал свободен;
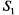 тАФ канал занят, очереди нет;
тАФ канал занят, очереди нет;
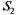 тАФ канал занят, одна заявка стоит в очереди;
тАФ канал занят, одна заявка стоит в очереди;
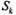 тАФ канал занят, k-1 заявок стоят в очереди;
тАФ канал занят, k-1 заявок стоят в очереди;
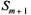 тАФ канал занят, т-заявок стоят в очереди.
тАФ канал занят, т-заявок стоят в очереди.
ГСП показан на рис. 4. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны 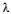 , а справа налево тАФ
, а справа налево тАФ 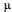 . Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево тАФ поток ВлосвобожденийВ» занятого канала, имеющий интенсивность
. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево тАФ поток ВлосвобожденийВ» занятого канала, имеющий интенсивность 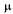 (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).
(как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).

Рис. 4. Одноканальная СМО с ожиданием
Изображенная на рис. 4 схема представляет собой схему размножения и гибели. Напишем выражения для предельных вероятностей состояний:
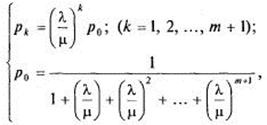 (5)
(5)
или с использованием: 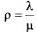 :
:
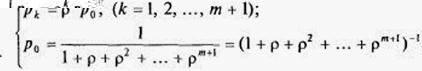 (6)
(6)
Последняя строка в (6) содержит геометрическую прогрессию с первым членом 1 и знаменателем р, откуда получаем:
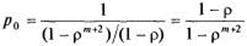 (7)
(7)
в связи с чем предельные вероятности принимают вид:
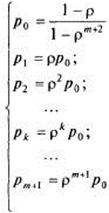 (8).
(8).
Выражение (7) справедливо только при 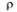 < 1 (при
< 1 (при 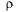 = 1 она дает неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем
= 1 она дает неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем 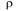 = 1 равна m+2, и в этом случае:
= 1 равна m+2, и в этом случае:
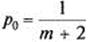 .
.
Определим характеристики СМО: вероятность отказа 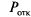 , относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди
, относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди 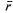 , среднее число заявок, связанных с системой
, среднее число заявок, связанных с системой 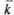 , среднее время ожидания в очереди
, среднее время ожидания в очереди 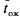 , среднее время пребывания заявки в СМО
, среднее время пребывания заявки в СМО 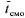 .
.
Вероятность отказа. Очевидно, заявка получает отказ только в случае, когда канал занят и все т-мест в очереди тоже:
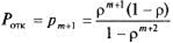 (9).
(9).
Относительная пропускная способность:
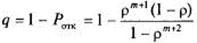 (10).
(10).
Абсолютная пропускная способность:
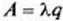 .
.
Средняя длина очереди. Найдем среднее число 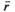 -заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины RтАФчисла заявок, находящихся в очереди:
-заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины RтАФчисла заявок, находящихся в очереди:
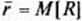 .
.
С вероятностью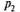 в очереди стоит одна заявка, с вероятностью
в очереди стоит одна заявка, с вероятностью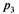 тАФ две заявки, вообще с вероятностью
тАФ две заявки, вообще с вероятностью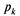 в очереди стоят k-1 заявок, и т.д., откуда:
в очереди стоят k-1 заявок, и т.д., откуда:
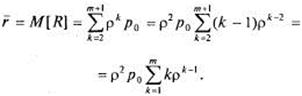 (11).
(11).
Поскольку 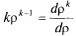 , сумму в (11) можно трактовать как производную по
, сумму в (11) можно трактовать как производную по 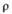 от суммы геометрической прогрессии:
от суммы геометрической прогрессии:
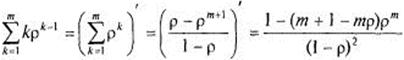 .
.
Подставляя данное выражение в (11) и используя 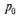 из (8), окончательно получаем:
из (8), окончательно получаем:
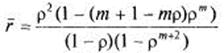 (12).
(12).
Среднее число заявок, находящихся в системе. Получим далее формулу для среднего числа 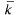 -заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку
-заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку 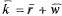 , где
, где 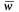 тАФ среднее число заявок, находящихся под обслуживанием, а k известно, то остается определить
тАФ среднее число заявок, находящихся под обслуживанием, а k известно, то остается определить 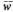 . Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью
. Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью 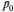 ) или 1 (с вероятностью 1 -
) или 1 (с вероятностью 1 - 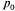 ), откуда:
), откуда:
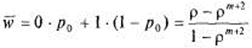 .
.
и среднее число заявок, связанных с СМО, равно:
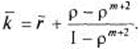 (13).
(13).
Среднее время ожидания заявки в очереди. Обозначим его 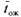 ; если заявка приходит в систему в какой-то момент времени, то с вероятностью
; если заявка приходит в систему в какой-то момент времени, то с вероятностью 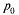 канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью
канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью 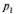 она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени
она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени 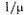 (среднее время обслуживания одной заявки). С вероятностью
(среднее время обслуживания одной заявки). С вероятностью 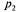 в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно
в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно 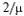 , и т.д.
, и т.д.
Если же k=m+1, т.е. когда вновь приходящая заявка застает канал обслуживания занятым и m-заявок в очереди (вероятность этого 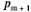 ), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
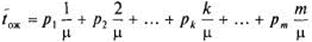 ,
,
если подставить сюда выражения для вероятностей (8), получим:
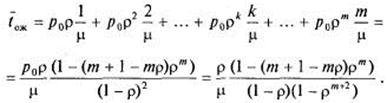 (14).
(14).
Здесь использованы соотношения (11), (12) (производная геометрической прогрессии), а также 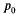 из (8). Сравнивая это выражение с (12), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
из (8). Сравнивая это выражение с (12), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
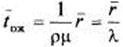 (15).
(15).
Среднее время пребывания заявки в системе. Обозначим 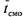 - матожидание случайной величины тАФ время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди
- матожидание случайной величины тАФ время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди 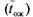 и среднего времени обслуживания
и среднего времени обслуживания 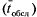 . Если загрузка системы составляет 100%, очевидно,
. Если загрузка системы составляет 100%, очевидно, 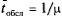 , в противном же случае:
, в противном же случае:
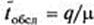 .
.
Отсюда:
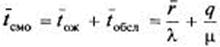 .
.
Пример 1. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 3). Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность 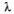 =1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
=1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
Определить:
вероятность отказа;
относительную и абсолютную пропускную способности АЗС;
среднее число машин, ожидающих заправки;
среднее число машин, находящихся на АЗС (включая обслуживаемую);
среднее время ожидания машины в очереди;
среднее время пребывания машины на АЗС (включая обслуживание).
Иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Находим вначале приведенную интенсивность потока заявок: 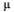 =1/1,25=0,8;
=1/1,25=0,8; 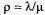 =1/0,8=1,25.
=1/0,8=1,25.
По формулам (8):
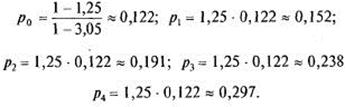
Вероятность отказа 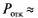 0,297.
0,297.
Относительная пропускная способность СМО: q=1-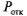 =0,703.
=0,703.
Абсолютная пропускная способность СМО: A=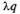 =0,703 машины в мин.
=0,703 машины в мин.
Среднее число машин в очереди находим по формуле (12):
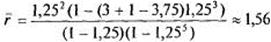 ,
,
т.е. среднее число машин, ожидающих в очереди на заправку, равно 1,56.
Прибавляя к этой величине среднее число машин, н
Вместе с этим смотрят:
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов