Методы решения алгебраических уравнений
В достаточно общем случае процесс решения прикладных задач состоит из следующих этапов:
1. постановка задачи и построение математической модели (этап моделирования);
2. выбор метода и разработка алгоритма (этап алгоритмизации) ;
3. запись алгоритма на языке, понятном ЭВМ (этап программирования);
4. отладка и исполнение программы на ЭВМ (этап реализации);
5. анализ полученных результатов (этап интерпретации).
Фабула практических задач связана с реальными объектами тАУ производственными процессами и явлениями природы, физическими закономерностями, экономическими отношениями и т.п. Решение задач обычно начинается с описания исходных данных и целей на языке строго определенных математических понятий. Точную формулировку условий и целей решения называют математической постановкой задачи. Этап исследования и описания их с помощью математических терминов называется построением математической модели или моделированием. Построение математической модели является наиболее сложным этапом решения задачи. Математическая модель может иметь вид уравнения, системы уравнений или быть выраженной в форме иных, как угодно сложных, математических структур или соотношений самой различной природы. Математические модели, в частности могут быть непрерывными или дискретными, в зависимости от того, какими величинами тАУ непрерывными или дискретными тАУ они описаны.
Вслед за построением математической модели идет этап поиска и разработки алгоритма решения задачи который называется алгоритмизацией.
Особые трудности на этапе поиска алгоритма заключается в поиске методе решения задачи. Дело в том, что уже для достаточно простых моделей чаще всего не удается получить результат в аналитической форме. Пусть, к примеру, задача свелась к решению уравнения с одной переменной: x - tg x = 0 . При всей тривиальности этой задачи выразить корни уравнения путем аналитических преобразований не удается, и весь арсенал методов ВлточнойВ» математики оказывается здесь беспомощным. В таких случаях приходится использовать приближенные математические методы, позволяющие получать удовлетворительные результаты. Основными методами решения подобных задач являются численные методы, при использовании которых результат получается путем вычислений. По этой причине наиболее естественный путь реализации численных методов тАУ это использование ЭВМ.
На следующем этапе алгоритм задачи записывается на языке, понятном ЭВМ. Это- этап программирования, затем следует этап реализации- исполнение программы на ЭВМ и получение результатов решения.
Завершающий этап решения задачи - это анализ, или интерпретация результатов. На этом этапе происходит осмысливание полученных результатов, сопоставление их с результатами контрольного просчета, а также с данными, полученными экспериментальным путем. При этом одни результаты могут оказаться приемлемыми, а другие тАУ противоречащими смыслу реальной задачи, такие решения следует отбросить. Высшим критерием пригодности полученных результатов в конечном итоге является практика.
В условиях использования ЭВМ численные методы являются мощным средством решения практических задач, хотя ЭВМ наоборот усложняет оценку точности получаемых результатов, как изложено в известном принципе Питера ВлЭВМ многократно увеличивает некомпетентность вычислителяВ».
На общую погрешность задачи влияет целый ряд факторов, начиная с построения математической модели до производства вычислений. Сюда входят: неустранимая погрешность, погрешность метода, вычислительная погрешность и в итоге, полная погрешность вытекает из суммы всех погрешностей. При решении конкретных задач те или иные виды погрешностей могу отсутствовать или незначительно влиять на конечный результат, тем не менее, в каждом случае необходим полный анализ погрешностей всех видов. Это в полной мере относится и к неустранимой погрешности тАУ погрешности математической модели.
К числу причин следует отнести также промахи, допускаемые в результате решения задачи: использование не тех данных, неверной программы вычислений и т.д. Поэтому необходима грубая прикидка ожидаемого результата, а это невозможно без ознакомления с понятиями приближенных методов вычислений, поэтом рассмотрим некоторые методы приближенных вычислений, применяемые в прикладной математике.
1. Решение нелинейных уравнений. Метод деления отрезка пополам. Метод касательных. Комбинированный метод хорд и касательных
Задача о нахождения приближенных значений действительных корней уравнения f(x)=0 предусматривает предварительное отделение корня, т.е. установление промежутка, в котором других корней данного уравнения нет. Будем предполагать, что функция f(x) в промежутке [a, b] непрерывна вместе со своим производным fтАЩ(x) и fтАЩтАЩ(x), значения f(a) и f(b) функции на концах промежутка имеют разные знаки, т. е. f(a)*f(b)<0, и обе производные fтАЩ(x) и fтАЩтАЩ(x) сохраняют знак во всем промежутке [a, b].
Так как действительным корнями уравнения f(x)=0 являются абсциссы точек пересечения кривой у = f(x) с осью Ox, то отделение корня можно произвести графически. Вместо уравнения у = f(x) можно взять уравнения у = rf (x), где r тАУ постоянная величина, отличная от нуля, так как уравнения f(x) =0 и rf (x) =0 равносильны.
Постоянную величину r можно взять так, чтобы ординаты точек графика не были чрезмерно большими или, наоборот, чтобы график не был слишком близок к оси Ox. Иногда бывает полезно уравнение f (x)=0 записать в виде 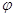 (x) =
(x) =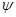 (x). Действительными корнями исходного уравнения служат абсциссы точек пересечения графиков функций y =
(x). Действительными корнями исходного уравнения служат абсциссы точек пересечения графиков функций y =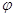 (x) и у =
(x) и у =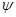 (x)
(x)
1.Метод деления отрезка пополам. Интервал изоляции действительно корня всегда можно уменьшить путем деления его, например, пополам, определяя, на границах какой из частей первоначального интервала функция f (x) меняет знак. Затем полученный интервал снова делят на две части и т.д. Такой процесс проводится до тех пор, пока не перестанут изменяться сохраняемые в ответ десятичные знаки.
2.Методкасательных. Пусть действительный корень уравнения f (x)=0 изолирован на отрезке [a, b]. Будем предполагать, что все ограничения, сформулированные выше относительно f(x), сохраняют силу и в этом случае. Возьмем на отрезке [a,b] такое число xo, при котором f(xo) имеет тот же знак, что и fn (xo), т.е. f(xo) 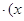 o) >0 (в частности, за xo может быть принят то из концов отрезка [a,b], в котором соблюдено это условие). Проведем в точке Mo[ xo; f (xo)] касательную к кривой y=f (x).За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ox. Это приближенное значение корня находится по формуле
o) >0 (в частности, за xo может быть принят то из концов отрезка [a,b], в котором соблюдено это условие). Проведем в точке Mo[ xo; f (xo)] касательную к кривой y=f (x).За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ox. Это приближенное значение корня находится по формуле
х1 = х0 - f(хо)/ fI (хо)
Применив этот прием вторично в точке M1[ x1; f (x1)], найдем
X2=X1 тАУ f (x1)/(x1)
и т. д. Полученная таким образом последовательность xo, x1,x2 тАж имеет своим пределом искомый корень.
Для оценки погрешности приближенного значения корня, найденного методом Ньютона, может быть использовано неравенство
| х - ξ | < [f(ξ) ]2/2 × max fII(х)/ [fI(х) ]3|
[a., b]
3. Комбинированный метод хорд и касательных. Пусть требуется найти действительный корень уравнения f (x)= 0, изолированный на отрезке [a,b]. Предполагается, что f (a) и f (b) имеют равные знаки, а каждая из производных сохраняет определенный знак на отрезке изоляции. Возьмем на отрезке [a,b] такую точку xo, что f (xo) и fтАЭ (xo) (при x, принадлежащем промежутку изоляции) имеют одинаковые знаки.
Воспользуемся формулами методов хорд и касательных:
X11=Xo- f (xo) / f1(xo); X12 = a тАУ (b тАУ a ) f (a) / f (b) тАУ f (a).
Величины X11 и X12 принадлежат промежутку изоляции, причем f (X11) и f (X12) имеют разные знаки.
X21=X11- f (x11) / f1(x11); X22=X11-(X12-X11) f (X11) / f (X12) тАУ f (X11).
Точки X21 и X22 на числовой оси расположены между точками X11 и X12, причем f (X21) и f (X22) имеют разные знаки.
Вычислим теперь значения
X31=X21- f (x21) / f1(x21); X32=X21-(X22-X21) f (X21) / f (X22) тАУ f (X21).
Каждая из последовательностей X11, X21, X31,.. Xn1, тАж; X12, X22, X32, тАж, Xn2, тАжстремится к искомому корню, причем одна из последовательностей монотонно возрастает, а другая тАУ монотонно убывает. Пусть, например, Xn1 < X< Xn2, тогда 0 < X- Xn-1 <  Xn2- Xn2 тАУ Xn1. Задав заранее достаточно малое
Xn2- Xn2 тАУ Xn1. Задав заранее достаточно малое  мы можем, увеличивая n, добиться выполнения неравенства Xn2 тАУ Xn1 <
мы можем, увеличивая n, добиться выполнения неравенства Xn2 тАУ Xn1 <  ; следовательно, при этом же значении n будет выполняться неравенство
; следовательно, при этом же значении n будет выполняться неравенство
X тАУ Xn1 <  . Таким образом, Xn1 является приближенным значением корня X, вычисленным с погрешностью, не превышающей
. Таким образом, Xn1 является приближенным значением корня X, вычисленным с погрешностью, не превышающей  .
.
Так, например, для нахождения приближенного значения X с точностью до 0,001 нужно определить n таким образом, чтобы значения Xn1 и Xn2, вычисленные с точностью до 0,001, совпадали.
2. Решение систем линейных алгебраических уравнений. Методом Крамера. Методом Гаусса. Метод Жордана Гаусса. Метод Зейделя
Решение систем линейных алгебраических уравнений тАУ одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности тАУ нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма. Одна из трудностей практического решения систем большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя объем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритмов линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памяти ЭВМ.
К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств тАУ сложные строительные конструкции и большие электрические цепи.
Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы невозможно, если бы соответствующие матрицы не являлись разреженными (матрица системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75 Гбайт).
Методом Крамера. Известно, что используя матрицы мы можем решать различные системы уравнений, причем эти системы могут быть какой угодно величины и иметь сколько угодно переменных. С помощью нескольких выводов и формул решение огромных систем уравнений становится довольно быстрым и более легким.
В частности, я опишу методы Крамера и Гаусса. Наилегчайшим способом является метод Крамера (для меня ), или как его еще называют тАУ формула Крамера. Итак, допустим, что мы имеем какую-либо систему уравнений
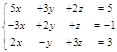 ,
,
в виде матрицы эту систему можно записать таким образом:
A = 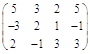 ,
,
где ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
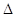 =
= 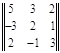 .
.
Основным определителем как вы уже заметили является матрица составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы будем заменять каждый столбец коэффициентов при переменной на столбец ответов уравнений. Итак, как я уже говорил, мы заменяем столбец при первой переменной на столбец ответов, затем при второй, конечно это все зависит от того, сколько переменных нам нужно найти.
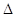 1 =
1 = 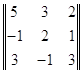 ,
, 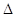 2 =
2 = 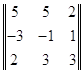 ,
,  3 =
3 = 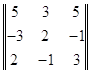 .
.
Затем нужно найти определители  1 ,
1 , 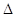 2 ,
2 , 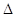 3 . Как находится определитель третьего порядка вы уже знаете. А вот здесь мы и применяем правило Крамера. Оно выглядит так:
3 . Как находится определитель третьего порядка вы уже знаете. А вот здесь мы и применяем правило Крамера. Оно выглядит так:
x1 = 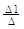 , x2 =
, x2 = 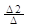 , x3 =
, x3 = 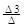
тАУ для данного случая, а в общем виде оно выглядит следующим образом: xi = 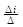 . Определитель составленный из коэффициентов при неизвестных, называется определителем системы.
. Определитель составленный из коэффициентов при неизвестных, называется определителем системы.
2. Метод Гаусса. Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Схема единственного деления. Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n - 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, тАж, n. Предположим, что коэффициент a11 ¹ 0. Будем называть его главным элементом 1-го шага.
Найдем величины
qi1 = ai1/a11 (i = 2, 3, тАж, n),
называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, тАж, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, тАж, qn1. Это позволит обратить в ноль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + тАж + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + тАж + a2n(1)xn = b2(1) ,
a32(1)x2 + a33(1)x3 + тАж + a3n(1)xn = b3(1) ,
an2(1)x2 + an3(1)x3 + тАж + ann(1)xn = bn(1).
в которой aij(1) и bij(1) вычисляются по формулам
aij(1) = aij − qi1a1j , bi(1) = bi − qi1b1.
2-й шаг. Целью этого шага является исключение неизвестного x2 из уравнений с номерами i = 3, 4, тАж, n. Пусть a22(1) ≠ 0, где a22(1) тАУ коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага
qi2 = ai2(1) / a22(1) (i = 3, 4, тАж, n)
и вычтем последовательно из третьего, четвертого, тАж, n-го уравнения системы второе уравнение, умноженное соответственно на q32, q42, тАж, qm2. В результате получим систему
a11x1 + a12x2 + a13x3 +тАж + a1nxn = b1,
a22(1)x2 + a23(1)x3 +тАж + a2n(1) = b2(1),
a33(2)x3 +тАж + a3n(2)xn = b3(2),
an3(2)x3 +тАж + ann(2)xn = bn(2).
Здесь коэффициенты aij(2) и bij(2) вычисляются по формулам
aij(2) = aij(1) тАУ qi2a2j(1) , bi(2) = bi(1) тАУ qi2b2(1).
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
k-й шаг. В предположении, что главный (ведущий) элемент k-го шага akk(kтАУ1) отличен от нуля, вычислим множители k-го шага
qik = aik(kтАУ1) / akk(kтАУ1) (i = k + 1, тАж, n)
и вычтем последовательно из (k + 1)-го, тАж, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на
qk+1,k, qk+2,k, тАж, qnk.
После (n - 1)-го шага исключения получим систему уравнений
a11x1 +a12x2 +a13x3 +тАж +a1nxn =b1,
a22(1)x2 +a23(1)x3 +тАж +a2n(1)xn =b2(1),
a33(2)x3 +тАж +a3n(2)xn =b3(2),
ann(nтАУ1)xn =bn(nтАУ1).
матрица A(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xnтАУ1. Осуществляя обратную подстановку, далее последовательно находим xnтАУ1, xnтАУ2, тАж, x1. Вычисления неизвестных здесь проводятся по формулам
xn = bn(nтАУ1) / ann(nтАУ1),
xk = (bn(kтАУ1) тАУ ak,k+1(kтАУ1)xk+1 тАУ тАУ akn(kтАУ1)xn) / akk(kтАУ1), (k = n тАУ 1, 1).
Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы akk(kтАУ1). Поэтому если один из главных элементов оказывыется равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). Описание метода. На k-м шаге прямого хода коэффициенты уравнений системы с номерами i = k + 1, тАж, n преобразуются по формулам
aij(k) = aij(kтАУ1) − qikakj , bi(k) = bi(kтАУ1) − qikbk(kтАУ1) , i = k + 1, тАж, n.
Интуитивно ясно, что во избежание сильного роста коэффициентов системы и связанных с этим ошибок нельзя допускать появления больших множителей qik.
В методе Гаусса с выбором главного элементоа по столбцу гарантируется, что |qik| ≤ 1 для всех k = 1, 2, тАж, n тАУ 1 и i = k + 1, тАж, n. Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на k-м шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент aikk при неизвестной xk в уравнениях с номерами i = k + 1, тАж, n. Затем соответствующее выбранному коэффициенту уравнение с номером ik меняют местами с k-м уравнением системы для того, чтобы главный элемент занял место коэффициента akk(k-1). После этой перестановки исключение неизвестного xk производят, как в схеме единственного деления.
Метод Гаусса с выбором главного элемента по всей матрице (схема полного выбора). В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов aij определяют максимальный по модулю элемент ai1j1. Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного xi1 из всех уравнений, кроме первого.
На k-м шаге метода среди коэффициентов aij(kтАУ1) при неизвестных в уравнениях системы с номерами i = k, тАж, n выбирают максимальный по модулю коэффициент aikjk(k-1). Затем k-е уравнение и уравнение, содержащее найденный коэффициент, меняют местами и исключают неизвестное xjk из уравнений с номерами i = k + 1, тАж, n.
На этапе обратного хода неизвестные вычисляют в следующем порядке: xjn, xjnтАУ1, тАж, xj1.
3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений
Ax =
с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду
x = Bx + c.
Здесь B тАУ квадратная матрица с элементами bij (i, j = 1, 2, тАж, n), c тАУ вектор-столбец с элементами cij (i = 1, 2, тАж, n).
В развернутой форме записи система имеет следующий вид:
x1 = b11x1 + b12x2 + b13x3 + тАж + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + тАж + b2nxn + c2
xn = bn1x1 + bn2x2 + bn3x3 + тАж + bnnxn + cn
Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.
Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:
x1 = a11тАУ1 (b1 тАУ a12x2 тАУ a13x3 тАУ тАж тАУ a1nxn),
из второго уравнения тАУ неизвестное x2:
x2 = a21тАУ1 (b2 тАУ a22x2 тАУ a23x3 тАУ тАж тАУ a2nxn),
и т. д. В результате получим систему
x1 = b12x2 +b13x3 +тАж +b1,nтАУ1xnтАУ1 +b1nxn+c1 ,
x2 = b21x1 +b23x3 +тАж +b2,nтАУ1xnтАУ1 +b2nxn+c2 ,
x3 = b31x1 +b32x2 +тАж +b3,nтАУ1xnтАУ1 +b3nxn+c3 ,
xn = bn1x1 +bn2x2 +bn3x3 +тАж +bn,nтАУ1xnтАУ1 +cn ,
в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам
bij = тАУaij / aii, ci = bi / aii (i, j = 1, 2, тАж, n, j ≠ i)
Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.
Описание метода. Введем нижнюю и верхнюю треугольные матрицы
 000тАж00b12b13тАжb1n
000тАж00b12b13тАжb1n
B1 =b2100тАж0B2 =00b23тАжb2n
b31b320тАж0, 000тАжb3n
bn1bn2bn3тАж0000тАж0
Заметим, что B =B1+B2 и поэтому решение x исходной системы удовлетворяет равенству
x = B1x + B2x + c.
Выберем начальное приближение x(0) = [x1(0), x2(0), тАж, xn(0)]T. Подставляя его в правую часть равенства при верхней треугольной матрице B2и вычисляя полученное выражение, находим первое приближение
x(1) = B1x(0) + B2x(1)
Подставляя приближение x(1), получим
x(2) = B1x(1) + B2x(2)
Продолжая этот процесс далее, получим последовательность x(0), x(1), тАж, x(n), тАж приближений к вычисляемых по формуле
x(k+1) = B1(k+1) + B2(k) + c
или в развернутой форме записи
x1(k+1) =b12x2(k) +b13x2(k) +тАж +b1nxn(k) +c1 ,
x2(k+1) =b21x1(k+1) +b23x3(k) + тАж +b2nxn(k) +c2 ,
x3(k+1) =b31x1(k+1) +b32x2(k+1) +тАж +b3nxn(k) +c3 ,
xn(k+1) =bn1x1(k+1) +bn2x2(k+1) +bn3x3(k+1) +тАж +cn.
Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим
xi(k+1) = xi(k) тАУ aiiтАУ1(∑j=1iтАУ1 aijxj(k+1) + ∑j=1n aijxi(k) тАУ bi).
Тогда достаточным условием сходимости метода Зейделя будет
∑j=1, j≠i n | aij | < | aii |
(условие доминирования диагонали).
Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.
4. Метод Жордана - Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое ВлмалоеВ» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана тАУ Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент ), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I тАУго уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 0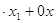 2+
2+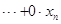 =bc
=bc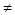 0.
0.
Это означает, что система не имеет решений, так как I тАУ му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I тАУ го уравнения обращаются в нуль. Это означает, что I тАУ ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + тАж + a1nxn = b1,n+1 |
a21x1 + a22x2 + тАж + a2nxn = b2,n+1 |
| am1x1 + am2x2 + тАж + amnxn = bm.n+1 |
Здесь x1, x2, тАж, xn тАФ неизвестные, которые надо определить. a11, a12, тАж, amn тАФ коэффициенты системы тАФ и b1, b2, тАж bm тАФ свободные члены тАФ предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = тАж = bm = 0), иначе тАФ неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу неизвестных.
Решение системы (1) тАФ совокупность чисел c1, c2, тАж, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), тАж, cn(1) и c1(2), c2(2), тАж, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), тАж, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
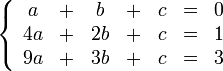
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
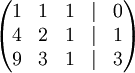
Проведём следующие действия:
В· К строке 2 добавим: -4 * Строку 1.
В· К строке 3 добавим: -9 * Строку 1.
Получим:
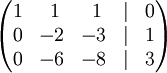
В· К строке 3 добавим: -3 * Строку 2.
В· Строку 2 делим на -2
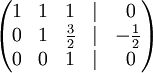
В· К строке 1 добавим: -1 * Строку 3.
В· К строке 2 добавим: -3/2 * Строку 3.
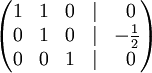
В· К строке 1 добавим: -1 * Строку 2.
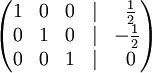
В правом столбце получаем решение:
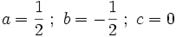 .
.
3. Математическая обработка результатов опыта. Аппроксимация функций. Полином Лагранжа. Метод наименьших квадратов
 В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функций.
В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функций.
Поводом для аппроксимации функции может послужить, в частности, табличный способ её задания. Предположим, что в результате некоторого эксперимента для конечного набора значений xi величины x из отрезка [a,b].
a=x0 < x1 <тАжxiтАж < xn= b
получен набор значений yi величины y (табл. 4.1). Если допустить, что между x и y существует функциональная зависимость y = F(x), можно поставить вопрос о поиске аналитического представления функции F (очевидно, что в такой общей постановке эта задача решается неоднозначно). Точки x0, x1,тАж xn в этом случае называются узлами. Если расстояние h=xi+1- x1 является постоянным (т.е. независящим от i ), то сетка значений, представленная табл. 4.1, называется равномерной.
Таблица 4.1
| x | x0 | x1 | x2 | тАж | x1 | тАж | xn |
| F(x) | Y0 | Y1 | Y2 | тАж | Y1 | тАж | yn |
Повод для аппроксимации может возникнуть даже тогда, когда аналитическое выражение для некоторой функции y = F(x) имеется. однако оно оказывается мало пригодным для решения поставленной задачи, потому что операция, которую требуется осуществить над этой функцией, трудновыполнима. Элементарный пример - вычисление значения трансцендентной функции ВлвручнуюВ». Действительно, чтобы вычислить , например, In 3,2756, проще всего воспользоваться степенным разложением функции, т.е. заменить трансцендентную функцию степенной. При этом получится, разумеется, приближенное значение функции, но если мы умеем контролировать погрешность, то можно считать, что мы получили интересующий нас результат тАУ хотя бы потому, что в реальности все равно приходится ограничиваться приближенным представлением значений логарифмической функции.
Другая ситуация, когда может потребоваться аппроксимация аналитически заданной функции, - вычисление определённых интегралов. Задача эта, как правило, весьма сложная, часто элементарными приемами невыполнимая. Как вычислить интеграл  Он, несомненно, существует, но по Формуле Ньютона тАУ Лейбница вычислен быть практически не может, так как первообразная
Он, несомненно, существует, но по Формуле Ньютона тАУ Лейбница вычислен быть практически не может, так как первообразная 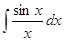 не выражается в элементарных функциях (как и множество других первообразных от элементарных функций). Аппроксимация подынтегральной функции - один из возможных приемов (и важно отметить, что цель аппроксимации налагает отпечаток на ее способ).
не выражается в элементарных функциях (как и множество других первообразных от элементарных функций). Аппроксимация подынтегральной функции - один из возможных приемов (и важно отметить, что цель аппроксимации налагает отпечаток на ее способ).
Классический подход к численному решению подобных задач заключается в том, чтобы, опираясь на информацию о функции F, по некоторому алгоритму подобрать аппроксимирующую функцию G, в определенном смысле ВлблизкуюВ» к F.
Чаще всего задача аппроксимации решается с помощью многочленов. Вычисления значений многочлена легко автоматизировать, производная и интеграл от многочлена, в свою очередь, также являются многочленами. Наряду с многочленами для аппроксимации используют ряды Фурье, экспоненциальные и другие элементарные функции.
Для оценки ВлблизостиВ» функций выбирают тот или иной критерий согласия. Эти критерии основаны на использовании той или иной метрики, т.е. способа введения расстояния между функциями, принадлежащими тому или иному классу:
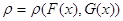 (см. гл. 2).
(см. гл. 2).
Например, для функций, ограниченных на отрезке [a,b] расстояние может быть введено следующим образом:
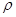 (F(x),G(x))=
(F(x),G(x))= 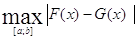 ;
;
для функций, непрерывных на отрезке [a,b], по формуле
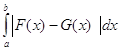
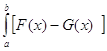 2dx
2dx
(а также многими другими способами).
Для функций, заданных таблично, достаточно распространенным критерием согласия является критерий Чебышева, который определяет расстояние 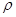 между аппроксимируемой и аппроксимирующей функциями как максимум величины отклонения между функциями в узлах сетки (см. табл. 4.1):
между аппроксимируемой и аппроксимирующей функциями как максимум величины отклонения между функциями в узлах сетки (см. табл. 4.1):
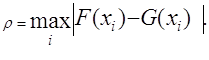 (4.1)
(4.1)
Если 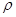 =0, т.е. F(xi)=G(xi)=yi, то соответствующий способ аппроксимации называют интерполяцией, а процедуру вычисления значений F(x) с помощью G(x) в точках, не являющихся узлами сетки, - интерполированием.
=0, т.е. F(xi)=G(xi)=yi, то соответствующий способ аппроксимации называют интерполяцией, а процедуру вычисления значений F(x) с помощью G(x) в точках, не являющихся узлами сетки, - интерполированием.
С геометрической точки зрения график функции G(x) при интерполировании должен проходить через все точки A0(x0,y0), A1(x1,y1),тАж, An(xn,yn). Подчеркнем, что для значений x, не являющихся узловыми, значения функции G(x) ничем не регламентированы, и в принципе могут значительно отличаться от значений функций F(x)).
Часто процедура аппроксимации связана с другим критерием согласия:
 (4.2)
(4.2)
Применяемый на его основе способ аппроксимации получил название метода наименьших квадратов.
Выбор критерия согласия позволяет строить методы, позволяющие однозначно определять параметры аппроксимирующей функции (если задан ее вид).
Полином Лагранжа.
Пусть Функция F(x) задана табл. 4.1. Построим многочлен Ln (x), степень которого не выше, чем n, и для которого выполнены условия интерполяции
Ln(x0)=y0, Ln(x1)=y1,тАж, Ln(xn)=yn. (4.6)
Будем искать Ln (x) в виде
Ln (x),=l0(x)+l1(x)+тАж+ln(x), (4.7)
где l1(x) тАУ многочлен степени n, причем
l1(xл)=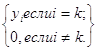 (4.8)
(4.8)
Очевидно, что требование (4.8) с учетом (4.7) вполне обеспечивает выполнение условий (4.6).
Многочлены l1(x)составим следующим образом:
l1(x)=Сi(x - x0)(x - x1) (xi - xi-1)(xi тАУ xi=1)
(xi - xi-1)(xi тАУ xi=1)  (xi тАУ xn) (4.9)
(xi тАУ xn) (4.9)
где Ci тАУ коэффициент, значение которого найдем из первой части условия (4.8):
Сi =
(заметим, что ни один множитель в знаменателе не равен нулю). Подставим Ci в (4.9) и далее с учетом (4.7) окончательно имеем:
Ln (x)=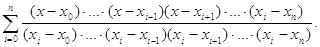 (4.10)
(4.10)
Это и есть интерполяционный многочлен Лагранжа. По таблице исходной функции F формула (4.10) позволяет довольно просто составить Влвнешний видВ» многочлена.
Метод наименьших квадратов.
1) На практике часто приходится решать такую задачу. пусть для двух функционально связанных величин x и y известны n пар соответствующих значений (x1,y1),(x2,y2),тАж,(xn,yn). Требуется в наперед заданной формуле y=f(x, a1, a2,тАж,am) определить m параметров a1, a2, тАж,am (mСчитается (исходя из принципов теории вероятностей), что наилучшими являются те значения a1, a2, тАж,am, которые обращают в минимум сумму

(т.е. сумму квадратов отклонений значений y, вычисленных по формуле, от заданных), поэтому сам способ и получил название способа наименьших квадратов.
Это условие дает систему m уравнений, из которых определяются a1,a2,тАж,am:
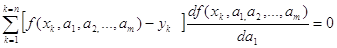 (1)
(1)
(f=1,2,тАж, m).
На практике заданную формулу y=f (xk,a1, a2, тАж, am) иногда приходится (в ущерб строгости полученного решения) преобразовывать к такому виду, чтобы систему (1) было проще решать (см. ниже подбор параметров в формулах y=Aecx и y=Axq). Частные случаи: а) y=a0xm-1+тАж+ am(m+1 параметров a0, a1, тАж, am;; n>m+1).
Система (1) принимает следующий вид:
 (2)
(2)
Эта система m+1 уравнений с m+1 неизвестными всегда имеет единственное решение, так как ее определитель отличен от нуля.