Побудова зображень предметiв на площинi
Житомирський Вiйськовий РЖнститут
Нацiонального Авiацiйного Унiврситету
Реферат
на тему:
Побудова зображень предметiв на площинi
Житомир 2010
Нарисна геометрiя тАУ наука, яка вивчаi просторовi форми та способи зображення iх на площинi.
Основною задачею нарисноi геометрii i вивчення методiв побудови зображень просторових форм та в розробцi способiв рiшення просторових задач за допомогою зображень.
Предмет, якiй зображують називають оригiналом або моделлю. Креслення повинно мiстити геометричну iнформацiю про форму та розмiри оригiналу. До такого креслення висуваються слiдуючи основнi вимоги:
тАУ наочнiсть, тобто давати просторове уявлення про модель;
тАУ простота з точки зору графiчного виконання;
тАУ точнiсть тАУ графiчнi операцii, якi виконуються на кресленнi, повиннi давати точнi рiшення.
Для побудови зображень предметiв на площинi користуються методом проекцiювання. Тому наступне питання - метод проекцiй.
1. Сутнiсть методу проекцiювання
Отже, проекцiя - це зображення предмета, "вiдкинуте" на площину за допомогою променiв. Спроекцiювати предмет тАФ це означаi зобразити його на площинi (рис.1).
Залежно вiд положення проекцiюючих променiв проекцii подiляють на центральнi та паралельнi.
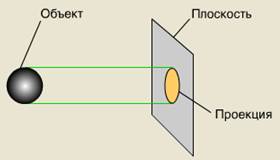
Рис. 1
РЖдею центрального проекцiювання видно з рис.2. Точка S, з якоi виходять проекцiюючi променi, називаiться центром проекцiювання. Площина π1 на яку проекцiюiться предмет, називаiться площиною проекцiй. Площина π1 i точка S становлять апарат центральноi проекцii. Щоб спроекцiювати трикутник, треба з центра проекцiй S через усi його вершини провести проекцiюючi променi до перетину з площиною проекцiй π1. Одержимо точки А1В1С1, якi називаються центральними проекцiями вершин А, В, С на площину π1, а трикутник А1В1С1 - центральною проекцiiю трикутника ABC.

Метод паралельного проекцiювання розглянемо за допомогою рис. 3. Як i в попередньому випадку, вибирають площину проекцiй π1. Замiсть центра проекцiй S задають напрям проекцiювання s, тобто вважають, що центр проекцiй S вiддалений у нескiнченнiсть. Тому проекцiюючi променi паралельнi мiж собою. Площина π1 i напрям s становлять апарат паралельноi проекцii. Щоб спроекцiювати трикутник ABC на площину π1, через вершини А, В, С проводять проекцiюючi променi паралельно напряму проекцiювання s. Внаслiдок перетину цих променiв з площиною π1 утворюiться трикутник А1В1С1, який являi собою паралельну проекцiю трикутника ABC.
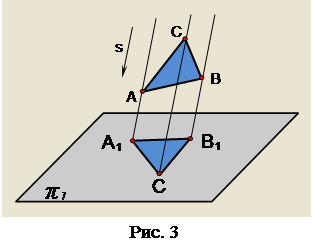

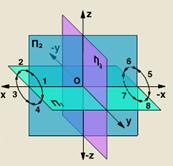
Рис. 5
Паралельнi проекцii подiляють на прямокутнi i косокутнi. Якщо проекцiюючi променi перпендикулярнi до площини проекцiй (рис. 4), то таке проекцiювання називають прямокутним, а проекцii, якi при цьому одержують тАФ прямокутними, або ортогональними. Якщо ж кут нахилу променiв не дорiвнюi 90В°, то такi паралельнi проекцii називаються косокутними. У кресленнi користуються прямокутними проекцiями.
Ортогональне проекцiювання маi ряд переваг перед центральним та косокутним паралельним проекцiюванням:
тАУ простоту геометричних побудов ортогональних проекцiй предметiв;
тАУ зберiгання на проекцiях, при певних умовах, форми та величини лiнiйних та кутових розмiрiв проекцiюючих предметiв.
2. Побудова за заданими координатами епюрiв прямих, взаiмного положення прямих та прямих i точок.
Розглянемо просторову модель координатноi площини проекцiй. Для визначення положення геометричноi фiгури в просторi i виявлення ii форми по ортогональних проекцiях найбiльш зручною i декартова система координат. Декартова система координат складаiться з трьох взаiмно перпендикулярних площин.
π1 тАУ горизонтальна площина проекцiй;
π2 тАУ фронтальна площина проекцiй;
π3 тАУ профiльна площина проекцiй.
Лiнii перетину площин проекцiй утворюють осi координат: X - вiсь абсцис, Y - вiсь ординат, Z - вiсь аплiкат, а точка перетину координатних осей O береться за початок координат.

π1 тАУ горизонтальна площина проекцiй; π2 тАУ фронтальна площина проекцiй;
Площини проекцiй перетинаються по вiсi координат Ох. Обертанням навколо вiсi Ох площину π1 сумiщають з площиною π2. Отримаiмо комплексне креслення
Схему побудови зворотного ортогонального креслення розвинув Гаспар Монж тАУ знаменитий французький учений. По схемi Монжа оригiнал (наприклад точка) проекцiюiться ортогонально на двi взаiмно перпендикулярнi площини проекцii π1 - горизонтальну i π2 - фронтальну площини проекцiй.
Лiнiя зв'язку - це пряма, що зтАЩiднуi двi проекцii точки на комплексному кресленнi i перпендикулярна осi проекцiй.
У результатi ми отримали двохпроекцiйне комплексне креслення точки А.
Твердження: Двi прямокутнi проекцii точки повнiстю визначають ii положення в просторi основних площин проекцiй.
Тобто комплексне креслення або епюр Монжа (з фр. ВлкресленняВ») тАУ це зображення, яке отримуiмо в результатi обертання площини проекцiй π1 на кут 90В° до сумiщення π2.
В кресленнi ж при побудовi зображень часто користуються трьома проекцiями на три площини проекцiй. Розглянемо, за якими законами це реалiзуiться.