Нарисна геометрiя

Нарисна геометрiя

Вступ

Засновником ВлНарисноi геометрiiВ» i видатний французький геометр кiнця VXIII тАУ початку XIX столiття Гаспар Монж. У своiму класичному творi ВлGeometry descriptiveВ» (Нарисна геометрiя), який був опублiкований у 1798 р., Г. Монж розробив загальну геометричну теорiю, яка надаi можливiсть на плоскому аркушi, який мiстить ортогональнi проекцii тривимiрного тiла, вирiшувати рiзнi стереометричнi задачi. Винайдений ним метод, метод ортогонального проецiювання на двi взаiмно перпендикулярнi площини проекцiй, до цього часу залишаiться iдиним способом створення креслення.

Предметом ВлНарисна геометрiяВ» i викладення та обТСрунтування методiв побудови зображень просторових фiгур на площини проекцiй та розвтАЩязання задач геометричного характеру за побудованими зображеннями. Нарисна геометрiя i кращим засобом розвитку в людини просторового уявлення, без якого неможлива iнженерна дiяльнiсть. Нарисна геометрiя i теоретичною базою для складання креслення. Креслення тАУ це своiрiдна мова, за допомогою якоi можна отримати зображення геометричних фiгур на площини проекцiй, застосовуючи лише точки, прямi та обмежений набiр геометричних iндексiв, букв та цифр. Мова ця iнтернацiональна, оскiльки зрозумiла будь тАУ якому iнженеру, незалежно вiд того, на якiй мовi вiн розмовляi та в якiй точцi Земноi кулi вiн живе.

1. Проекцii точки

Будь-яку геометричну фiгуру розглядають як множину точок, якi iй належать. Тому проекцii геометричноi фiгури на площини проекцiй отримують шляхом проецiювання належних iй точок на площини проекцiй.

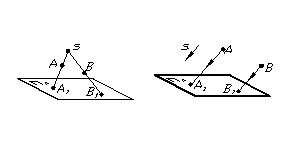
Усi побудови, якi виконуються у нариснiй геометрii, базуються на методi проецiювання. Залежно вiд апарату проецiювання проекцii подiляють на центральнi та паралельнi (рис. 1.1).

Центральною проекцiiю точки називають точку перетину променя, проведеного через задану точку простору (А, В), та центр проекцiй S з площиною проекцiй (П₁). (рис. 1.1 а).

Центральне проецiювання найчастiше застосовують у архiтектурi, в машинобудуваннi застосовуiться паралельне проецiювання.

а) б)

Рисунок 1.1 тАУ Методи проецiювання: а) центральне; б) паралельне

Залежно вiд напрямку проецiювання паралельне проецiювання подiляють на косокутне (напрямок проецiювання не перпендикулярний площинi проекцiй) та прямокутне (напрямок проецiювання перпендикулярний площинi проекцiй). Прямокутне проецiювання найчастiше називають ортогональним. Ортогональною проекцiiю точки називають точку перетину променя, проведеного через точку простору перпендикулярно площинi проекцiй, з площиною проекцiй.

Як для центрального, так i для паралельного проецiювання справедливе твердження, що будь-якiй точцi простору вiдповiдаi одна iдина центральна (або паралельна) ii проекцiя. Але при такому апаратi проецiювання по центральнiй (або паралельнiй) проекцii точки однозначно неможливо встановити ii положення у просторi. Необхiдно мати якусь допомiжну умову. Такою допомiжною умовою i проецiювання на двi площини проекцiй.

1.1 Проекцii точки на двi взаiмно перпендикулярнi площини проекцiй

Щоб отримати ортогональнi проекцii точки на двi взаiмно перпендикулярнi площини проекцiй, необхiдно з точки простору (точка А) послiдовно провести перпендикуляри до перетину iх з горизонтальною та фронтальною площинами проекцiй (рис. 1.2).На рисунку 1.2 використанi такi позначення: П₁ тАУ горизонтальна площина проекцiй; П₂ тАУ фронтальна площина проекцiй; О тАУ початок координат; Х, У, Z тАУ осi координат; А тАУ точка у просторi; А₁ та А₂ тАУ вiдповiдно горизонтальна та фронтальна проекцii точки.

Рисунок 1.2 тАУ Проекцii точки на двi площини проекцiй

Для побудови комплексного креслення або епюра Монжа (рис. 1.3) необхiдно площину П₂ залишити без змiн, а площину П₁ розвернути на 90⁰ вниз до сумiщення з площиною П₂. Послiдовно вимiряти та вiдкласти на вiдповiдних осях абсцису, ординату та аплiкату точки (рис. 1.3).

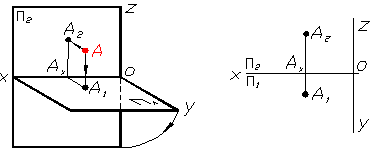
Рисунок 1.3 тАУ Побудова епюра Монжа

1.2 Проекцii точки на три взаiмно перпендикулярнi площини проекцiй

Щоб отримати ортогональнi проекцii точки на три взаiмно перпендикулярнi площини проекцiй, необхiдно через точку простору послiдовно провести перпендикуляри на горизонтальну, фронтальну та профiльну площини проекцiй (рис. 1.4). У перетинi проведених перпендикулярiв з кожною з площин проекцiй одержують ортогональнi проекцii точки А: горизонтальну (А₁), фронтальну (А₂) та профiльну (А₃) проекцii точок.

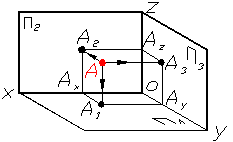
Рисунок 1.4 тАУ Проекцii точки на три площини проекцiй

На рисунку 1.4 використанi такi позначення: П₁, П₂, П₃ тАУ вiдповiдно горизонтальна, фронтальна та профiльна площини проекцiй;О тАУ початок координат; Х, У, Z тАУ осi координат; А тАУ точка у просторi; А₁, А₂, А₃ тАУ проекцii точки А вiдповiдно на П₁, П₂, П₃.

Для побудови комплексного креслення (епюр Монжа) необхiдно площину П₂ залишити без змiн, площину П₁ розвернути на 90⁰ вниз, а площину П₃ розвернути на 90⁰ на право до сумiщення з площиною П₂ (рис. 1.5). Послiдовно вимiряти та вiдкласти на вiдповiдних осях абсцису, ординату та аплiкату точки А.

Рисунок 1.5 тАУ Епюр Монжа

1.3 Основнi властивостi ортогонального проецiювання

1 Положення точки у просторi визначаiться трьома ii координатами (X, Y, Z).

2 Горизонтальна проекцiя точки визначаiться ii абсцисою (Х) та ординатою (У), фронтальна проекцiя точки тАУ ii абсцисою (Х) та аплiкатою (Z), профiльна проекцiя точки тАУ ii ординатою (У) та аплiкатою (Z).

Наслiдки:

1 Вiддалення точки вiд площин проекцiй визначаiться вiдповiдними координатами:

- координатою Х тАУ вiд площини П₃;

- координатою У тАУ вiд площини П₂;

- координатою Z тАУ вiд площини П₁.

2 Однойменнi проекцii точок знаходяться на однiй лiнii проецiйного звтАЩязку, перпендикулярнiй до вiдповiдноi осi.

3 Положення точки у просторi визначаiться двома ii проекцiями, тому за двома проекцiями точки завжди можна побудувати ii третю проекцiю.

Приклад 1 За двома проекцiями точки А визначити ii третю проекцiю.

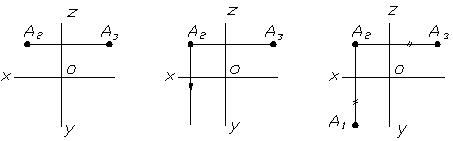
а) б) в)

Рисунок 1.6 тАУ Побудова третьоi проекцii точки

За умовами задачi данi двi проекцii точки: фронтальна та профiльна (рис. 1.6а). Для побудови горизонтальноi проекцii точки А необхiдно з фронтальноi проекцii точки провести лiнiю проецiйного звтАЩязку, перпендикулярну до осi Х (рис. 1.6б), на якiй вiдкласти ординату точки (рис. 1.6в), яка вимiряiться на профiльнiй площинi проекцiй (вiдстань позначено двома штрихами).

Аналогiчно можна побудувати фронтальну проекцiю точки за ii горизонтальною та профiльною проекцiями або профiльну проекцiю точки за горизонтальною та фронтальною проекцiями.

2. Проекцii прямоi

Положення прямоi у просторi визначаiться положенням двох точок, якi iй належать. Тому для побудови комплексного креслення прямоi достатньо мати проекцii двох точок, якi iй належать (рис. 1.7).

Рисунок 1.7 тАУ Проекцii прямоi лiнii

2.1 Положення прямоi вiдносно площин проекцiй

Залежно вiд положення прямоi вiдносно площин проекцiй прямi подiляють на прямi загального положення та особливого положення.

Прямими загального положення називають прям, не паралельнi жоднiй з площин проекцiй (рис. 1.7).

Прямi особливого положення подiляють на прямi рiвня та прямi проецiювальнi.

Прямi рiвня тАУ це прямi, якi паралельнi однiй з площин проекцiй. Залежно вiд того, якiй площинi проекцiй пряма паралельна, iх подiляють на прямi горизонтального, фронтального та профiльного рiвня. На рисунку 1.8 наведенi приклади прямих рiвня: АВ тАУ фронтальна пряма рiвня, CD тАУ горизонтальна пряма рiвня, EF тАУ профiльна пряма рiвня.

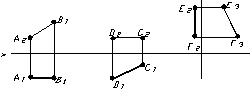
Рисунок 1.8 тАУ Прямi рiвня

Прямi проецiювальнi (рис. 1.9) тАУ це прямi, якi паралельнi одночасно двом площинам проекцiй, тобто перпендикулярнi до третьоi, на яку вони проектуються у виглядi точки. Залежно вiд того, до якоi площини проекцiй прямi перпендикулярнi, iх називають горизонтально-проецiювальними (вiдрiзок EF), фронтально-проецiювальними (вiдрiзок CD) та профiльно-проецiювальними (вiдрiзок AB).

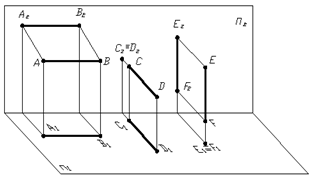
Рисунок 1.9 тАУ Прямi проецiювальнi

Комплексне креслення (епюр Монжа) проецiювальних прямих наведене на рисунку 1.10.

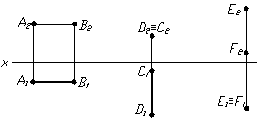
Рисунок 1.10 тАУ Комплексне креслення проецiювальних прямих

2.2 Визначення натуральноi величини вiдрiзка способом прямокутного трикутника

Аналiзуючи положення вiдрiзкiв прямоi вiдносно площин проекцiй, можна зробити висновок, що лише у тому випадку, коли вiдрiзок прямоi займаi особливе положення, на комплексному кресленнi маiмо натуральну величину вiдрiзка. Для прямих загального положення на площини проекцiй вiдрiзок прямоi проектуiться iз спотворенням. При розвтАЩязаннi багатьох задач нарисноi геометрii досить часто виникаi необхiднiсть мати натуральнi величини вiдрiзкiв прямих лiнiй. Натуральну величину вiдрiзка, який займаi загальне положення, можна визначити способом прямокутного трикутника (рис. 1.11). Суть способу полягаi в тому, що натуральну величину вiдрiзка (НВ) визначають як гiпотенузу прямокутного трикутника, у якого один катет тАУ це проекцiя вiдрiзка на площину проекцiй, а другий тАУ рiзниця вiдстаней кiнцiв вiдрiзка вiд цiii площини проекцiй. Цей спосiб проiлюстрований на рисунку 1.11, де: АВ тАУ вiдрiзок у просторi; А₁В₁ тАУ горизонтальна проекцiя вiдрiзка; Z тАУ рiзниця вiдстаней кiнцiв вiдрiзка АВ вiд горизонтальноi площини проекцiй; a тАУ кут нахилу вiдрiзка АВ до горизонтальноi площини проекцiй.

Рисунок 1.11 тАУ Визначення натуральноi величини вiдрiзка

На рисунку 1.12 (а та б) наведений приклад визначення натуральноi величини вiдрiзкiв та кутiв нахилу iх до вiдповiдних площин проекцiй.

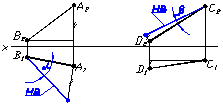
а) б)

Рисунок 1.12 тАУ Визначення натуральноi величини вiдрiзка та кутiв нахилу його до площин проекцiй

3. Проекцii площини

РЖснують шiсть способiв завдання площини у просторi: трьома точками, якi не належать однiй прямiй, прямою та точкою, яка не належить цiй прямiй, двома паралельними прямими, двома прямими, якi перетинаються, геометричною фiгурою (вiдтинання площини), слiдами площини.

3.1 Способи завдання площини на комплексному кресленнi

На комплексному кресленнi площина може бути задана:

- проекцiями трьох точок, якi не належать однiй прямiй (рис. 1.13);

- проекцiями прямоi та точки, яка не належить цiй прямiй (рис. 1.14);

-

Рисунок 1.13 Рисунок 1.14

- проекцiями двох паралельних прямих (рис. 1.15);

- проекцiями двох прямих, якi перетинаються (рис. 1.16);

-

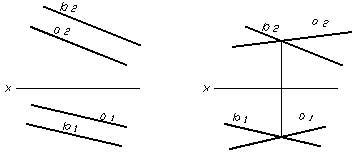
Рисунок 1.15Рисунок 1.16

проекцiями вiдтинання площини (рис. 1.17);

- слiдами площини (рис. 1.18).

-

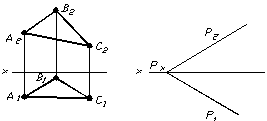
Рисунок 1.17 Рисунок 1.18

3.2 Положення площини вiдносно площини проекцiй

Залежно вiд положення заданих площин вiдносно площин проекцiй iх подiляють на площини загального положення та площини особливого положення.

Площинами загального положення називають площини, якi не перпендикулярнi до жодноi з площин проекцiй. Приклади площин загального положення наведенi на рисунках 1.13 тАУ 1.18.

Площини особливого положення подiляють на площини проецiювальнi та площини рiвня.

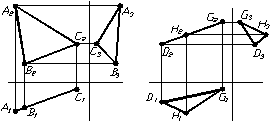
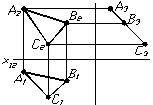
Якщо задана площина перпендикулярна до однiii з площин проекцiй, то вона на неi проектуiться у виглядi вiдрiзка. Такi площини називаються проецiювальними. Залежно вiд того, якiй площинi проекцiй заданi площини перпендикулярнi, iх називають горизонтально тАУ проецiювальними (рис. 1.19а), фронтально тАУ проецiювальними (рис. 1.19б) та профiльно-проецiювальними (рис. 1.19в).

а) б) в)

Рисунок 1.19 тАУ Площини проецiювальнi

Площини рiвня тАУ це площини, якi перпендикулярнi одночасно до двох площин проекцiй, тобто паралельнi третiй площинi проекцiй, на яку вони проектуються у натуральну величину.

Залежно вiд того, якiй площинi проекцiй задана площина паралельна, площини називають площинами горизонтального рiвня (рис. 1.20а), фронтального рiвня (рис. 1.20б) та профiльного рiвня (рис. 1.20в).

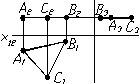
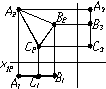
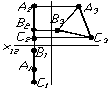
а) б) в)

Рисунок 1.20 тАУ Площини рiвня

3.3 Належнiсть точки та прямоi площинi

1 Пряма належить площинi, якщо вона проходить через двi точки, якi iй належать (рис. 1.21а).

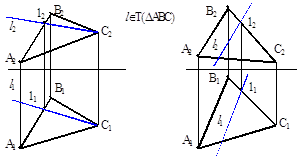
а) б)

Рисунок 1.21 тАУ Належнiсть прямоi площинi

2 Пряма належить площинi, якщо вона проходить через точку, яка належить цiй площинi та паралельна прямiй, яка знаходиться у площинi (рис. 1.21б).

Точка належить площинi, якщо вона знаходиться на прямiй, належнiй площинi. На рисунку 1.22а точка 1 належить площинi трикутника АВС, оскiльки точка належить сторонi АВ трикутника АВС. На рисунку 1.22б точка 2 не належить площинi трикутника АВС.

а) б)

Рисунок 1.22 тАУ Належнiсть точки прямiй

3.4 Головнi лiнii площини

До прямих, якi займають особливе положення, вiдносять горизонталi, фронталi, профiльнi прямi та прямi найбiльшого нахилу до площин проекцiй.

Горизонталями площини (h) називають прямi, якi належать площинi та паралельнi горизонтальнiй площинi проекцiй. На рисунках 1.23а (площина задана прямою та точкою, яка не належить цiй площинi) та 1.23б (площина задана слiдами) наведенi приклади побудови горизонталей площин.

Побудову горизонталi починають з ii фронтальноi проекцii (h₂), оскiльки вона паралельна осi Х_12. Горизонтальну проекцiю (h₁) визначають по лiнiях проецiйного звтАЩязку.

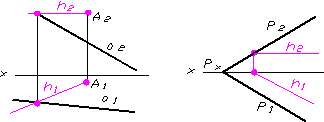
а) б)

Рисунок 1.23 тАУ Побудова горизонталi площини

Фронталями площини (f) називають прямi, якi належать площинi та паралельнi фронтальнiй площинi проекцiй. На рисунку 1.24а та б наведенi приклади проведення фронталей площин, якi заданi рiзними способами.

Побудову фронталi починають з ii горизонтальноi проекцii (f₁), оскiльки вона паралельна осi Х₁₂, ii фронтальну проекцiю (f₂) визначають по лiнiях проецiйного звтАЩязку.

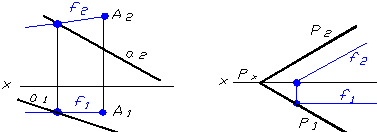
а) б)

Рисунок 1.24 тАУ Побудова фронталi площини

Профiльними прямими називають прямi, якi належать площинi та паралельнi профiльнiй площинi проекцiй.

Лiнiями найбiльшого нахилу до площини проекцiй називають прямi, якi належать заданiй площинi та паралельнi горизонталi, фронталi або профiльнiй прямiй. Лiнii найбiльшого нахилу до площин проекцiй дають можливiсть визначати кути нахилу до вiдповiдних площин проекцiй.

4. Перетворення комплексного креслення

Аналiзуючи положення прямих та площин стосовно площин проекцiй зрозумiло що, лише у тому випадку, коли вони займають особливе положення (рисунки 1.8, 1.10, 1.20), на однiй (або двох) площинi проекцiй матимемо натуральну величину. Якщо прямi чи площини займають загальне положення, натуральноi величини бути не може. Для визначення натуральноi величини розмiрiв площини чи вiдрiзка iснуi кiлька способiв: замiна площин проекцiй, обертання навколо проецiювальноi осi, обертання навколо прямоi рiвня, плоскопаралельне перемiщення.

Щоб визначити натуральну величину геометричного обтАЩiкта, необхiдно або змiнити систему площин проекцiй так, щоб обтАЩiкт зайняв особливе положення, або розвернути сам обтАЩiкт у просторi так, щоб вiн зайняв особливе положення стосовно iснуючоi системи площин проекцiй.

4.1 Спосiб замiни площин проекцiй

Суть способу полягаi в тому, що положення геометричного обтАЩiкта у просторi залишаiться незмiнним, а одну з площин проекцiй замiнюють новою, яка створюi з другою площиною проекцiй нову систему взаiмно перпендикулярних площин, вiдносно якоi геометричний обтАЩiкт займе особливе положення. Замiн може бути декiлька. Способом замiни площин можна розвтАЩязувати багато позицiйних та метричних задач нарисноi геометрii.

Приклад 2 Визначити натуральну величину вiдрiзка АВ.

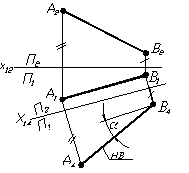
Рисунок 1.25 тАУ Визначення натуральноi величини вiдрiзка способом замiни площин проекцiй

Для визначення натуральноi величини вiдрiзка необхiдно ввести допомiжну площину проекцiй П₄, яка перпендикулярна до горизонтальноi площини проекцiй та паралельна вiдрiзку АВ.

Площина П₄ вводиться на будь тАУ якiй вiдстанi вiд вiдрiзка АВ. На комплексному кресленнi достатньо провести нову вiсь Х₁₄ паралельно горизонтальнiй проекцii вiдрiзка АВ та з А₁ та В₁ провести лiнii звтАЩязку, перпендикулярнi до осi Х_14, на яких вiдкласти вiддалення вiд горизонтальноi площини проекцiй, якi вимiрюються на площинi П₂ (зробленi позначки однiiю та двома рисками). На рисунку 1.25 позначений кут нахилу (a) прямоi АВ до горизонтальноi площини проекцiй тАУ це буде кут мiж НВ прямоi АВ та прямою паралельною осi Х₁₄.

Щоб визначити кут нахилу прямоi АВ до фронтальноi площини проекцiй, необхiдно ввести площину, перпендикулярну до площини П₂ та паралельну вiдрiзку АВ.

Приклад 3 Визначити натуральну величину трикутника АВС (рис. 1.26).

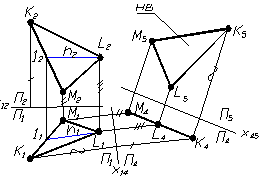
Рисунок 1.26 тАУ Визначення натуральноi величини трикутника способом замiни площин проекцiй

Для розвтАЩязання задачi двiчi виконують замiну площин проекцiй.

Перша замiна виконана таким чином, щоб трикутник перетворити у проецiювальну площину. Для цього необхiдно нову вiсь Х₁₄ провести перпендикулярно до горизонтальноi проекцii горизонталi (h₁) тАУ це ознака того, що трикутник перпендикулярний до новоi площини проекцiй (П₄), на яку вiн проектуiться у вiдрiзок.

Друга замiна виконана таким чином, щоб трикутник перетворити у площину рiвня. Для досягнення цього необхiдно нову вiсь Х₄₅ провести паралельно вiдрiзку, в який спроектувався трикутник АВС.

Вiдстанi, якi необхiдно вимiряти та вiдкласти вiд нових осей, позначенi вiдповiдними лiнiями.

4.2 Спосiб обертання навколо проецiювальноi осi

Суть способу полягаi в тому, що система площин проекцiй залишаiться незмiнною, а геометричний елемент змiнюi своi положення у просторi, займаючи особливе положення вiдносно площин проекцiй. Усi точки геометричного обтАЩiкта обертаються у площинах, паралельних тiй площинi проекцiй, вiдносно якоi вiсь обертання перпендикулярна. Якщо вiсь обертання перпендикулярна до горизонтальноi площини проекцiй, то на комплексному кресленнi всi горизонтальнi проекцii точок геометричного обтАЩiкта пересуваються по

колах, а фронтальнi проекцii тАУ по прямих, паралельних осi Х.

Приклад 4 Визначити натуральну величину трикутника АВС (рис. 1.27).

Рисунок 1.27 тАУ Визначення натуральноi величини трикутника способом обертання навколо проецiювальноi осi

Для визначення натуральноi величини трикутника АВС необхiдно провести горизонталь площини.

Першим обертанням трикутник переведено у проецiювальне положення. Обертання виконано навколо прямоi, проведеноi через точку А, перпендикулярноi до площини П₁.

Друге обертання виконано навколо прямоi, проведеноi через точку В, перпендикулярно до площини П₂. Трикутник переведений у положення паралельностi площинi П₁, тому горизонтальна проекцiя трикутника тАУ це його натуральна величина.

Основним недолiком способу обертання навколо проецiювальноi осi i накладання одного зображення на iнше. При розвтАЩязаннi задач способом плоскопаралельного перемiщення цього недолiку немаi.

4.3 Спосiб плоскопаралельного перенесення

Суть способу полягаi в тому, що система площин залишаiться незмiнною, а геометричний обтАЩiкт займаi особливе положення вiдносно площин проекцiй, що даi можливiсть розвтАЩязувати позицiйнi та метричнi задачi. Цей спосiб вважають винятковим способом обертання навколо проецiювальноi осi. На комплексному кресленнi одна з проекцiй геометричного обтАЩiкта, не змiнюючи своiх розмiрiв, змiнюi своi положення вiдносно осi Х₁₂. Тодi всi точки другоi проекцii пересуваються по прямих, паралельних осi Х₁₂.

Приклад 5 Визначити натуральну величину вiдрiзка АВ.

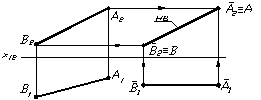
Рисунок 1.28 тАУ Визначення натуральноi величини вiдрiзка способом плоско паралельного перемiщення

У даному прикладi для визначення натуральноi величини вiдрiзка способом плоскопаралельного перемiщення горизонтальну проекцiю вiдрiзка (А₁ В₁) розмiщують на вiльному мiсцi креслення паралельно осi Х₁₂. Фронтальна проекцiя вiдрiзка АВ буде його натуральною величиною. Для ii побудови необхiдно з фронтальних проекцiй точок А₂ та В₂ провести лiнii, паралельнi осi Х₁₂ до перетину з лiнiями проекцiйного звтАЩязку, проведених вiд горизонтальних проекцiй цих точок.

Приклад 6 Визначити натуральну величину трикутника АВС.

Рисунок 1.29 тАУ Визначення натуральноi величини трикутника способом плоскопаралельного перемiщення

Щоб визначити натуральну величину трикутника АВС, необхiдно спочатку перетворити площину загального положення в площину проецiювальну (у наведеному прикладi тАУ фронтально тАУ проецiювальну), а потiм у площину рiвня (на рисунку 1.29 тАУ це площина горизонтального рiвня). Для виконання таких перетворень перш за все необхiдно провести горизонталь площини трикутника.

Щоб перетворити площину загального положення у площину фронтально проецiювальну, необхiдно горизонтальну проекцiю трикутника розмiстити так, щоб горизонталь його стала перпендикулярна до осi Х. У цьому разi всi фронтальнi проекцii вершин трикутника будуть пересуватися паралельно осi Х до перетину з лiнiями звтАЩязку, проведеними з горизонтальних проекцiй вершин трикутника АВС. На фронтальну площину проекцiй трикутник проектуiться у виглядi вiдрiзка прямоi лiнii.

Щоб перетворити площину фронтально-проецiювальну у площину горизонтального рiвня, необхiдно фронтальну проекцiю трикутника (вiдрiзок прямоi) розмiстити паралельно осi Х тАУ тодi горизонтальнi проекцii вершин трикутника будуть пересуватися паралельно осi Х до перетину з вiдповiдними лiнiями звтАЩязку. Горизонтальна проекцiя трикутника тАУ це натуральна величина його.

5. Поверхнi

Свiт поверхонь багатогранний та рiзноманiтний. РЖз усього рiзноманiття найбiльш поширеними i багатогранники та поверхнi обертання.

Багатогранниками називають поверхнi, якi обмеженi площинами (гранями). До багатогранникiв вiдносять призми та пiрамiди (рис. 1.30).

Рисунок 1.30 тАУ Багатогранники

Залежно вiд того, яка геометрична фiгура i основою багатогранника, iх називають тригранними, чотиригранними, птАЩятигранними призмами чи пiрамiдами.

Поверхнi обертання утворенi обертанням твiрноi (прямоi або кривоi лiнii) навколо нерухомоi осi. До поверхонь обертання вiдносять конус, цилiндр, сферу, тор. На рисунку 1.31 наведенi комплекснi креслення конуса, цилiндра, сфери та тора.

Рисунок 1.31 тАУ Поверхнi обертання

5.1 Точки на поверхнях

Для побудови проекцii точки, яка належить поверхнi, за заданою проекцiiю необхiдно перш за все зтАЩясувати, якому елементу поверхнi точка належить.

Якщо точка належить поверхнi призми чи пiрамiди, то для побудови другоi проекцii точки достатньо провести лiнii проекцiйного звтАЩязку. При побудовi проекцiй точок, якi належать будь-якiй поверхнi, необхiдно памтАЩятати про видимiсть. Невидимi проекцii точок позначають у дужках, наприклад, (А₁) тАУ горизонтальна проекцiя точки А невидима.

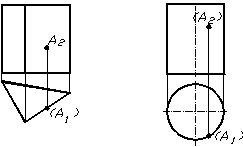
Рисунок 1.32 тАУ Точки на поверхнях

На рисунку 1.32 наведенi приклади побудови горизонтальних проекцiй точок, якi належать поверхням пiрамiди та цилiндра. Заданi фронтальнi проекцii точок. Для побудови горизонтальних проекцiй точок необхiдно провести лiнii звтАЩязку на вiдповiднi елементи поверхонь з урахуванням видимостi. У наведених прикладах для поверхнi призми фронтальна проекцiя точки А видна, ii горизонтальна проекцiя тАУ невидна. На поверхнi цилiндра тАУ фронтальна та горизонтальнi проекцii точки А не виднi.

Для визначення точок, якi належать поверхням пiрамiди або конуса, необхiдно виконати допомiжнi побудови.

Якщо точка належить ребру пiрамiди, то для побудови другоi проекцii точки необхiдно провести лiнiю звтАЩязку на вiдповiдне ребро. У наведеному на рисунку 1.33а прикладi шукана точка D знаходиться на ребрi SC. За умовами задачi задана фронтальна проекцiя точки D. Для побудови ii горизонтальноi проекцii достатньо провести лiнiю звтАЩязку на горизонтальну проекцiю ребра SC.

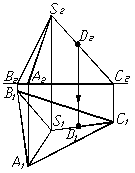
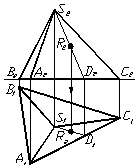
а) б)

Рисунок 1.33 тАУ Точки на поверхнi пiрамiди

Якщо точка належить гранi пiрамiди, то через задану точку у вiдповiднiй гранi необхiдно провести допомiжну пряму.

У наведеному прикладi задана фронтальна проекцiя точки R. Точка R належить гранi SAC. Для побудови ii горизонтальноi проекцii послiдовно виконують такi дii:

- через задану точку на гранi SAC провести фронтальну проекцiю допомiжноi прямоi SD;

- побудувати горизонтальну проекцiю допомiжноi прямоi (S₁D₁);

- по лiнii проецiйного звтАЩязку визначити горизонтальну проекцiю точки R на гранi ASC.

5.2 Перетин поверхонь проецiювальними площинами

Якщо будь-яку геометричну поверхню перетнути проецiювальною площиною, то одна з проекцiй лiнii перетину очевидна тАУ це вiдрiзок прямоi лiнii, який збiгаiться з проекцiiю проецiювальноi площини. Другу проекцiю лiнii перетину будують за точками, якi iй належать.

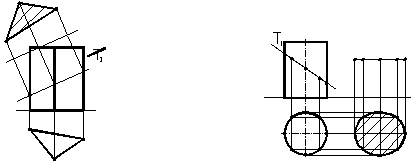
Якщо проецiювальна площина перетинаi поверхню призми або цилiндра, нiякi побудови не виконуються, а лише позначаються проекцii лiнii перетину. На рисунку 1.34 наведенi приклади побудови проекцiй лiнii перетину призми та цилiндра фронтально-проецiювальними площинами та визначена натуральна величина перерiзiв способом замiни площин проекцiй (для призми) та способом плоскопаралельного перемiщення (для цилiндра).

а) б)

Рисунок 1.34 тАУ Перетин призми та цилiндра фронтально-проецiювальними площинами

Горизонтальна проекцiя фiгури перерiзу пiрамiди фронтально-проецiювальною площиною наведена на рисунку 1.35 Для ii побудови проведенi лiнii проецiйного звтАЩязку на вiдповiднi ребра пiрамiди. Натуральна величина фiгури перетину визначена способом плоскопаралельного перемiщення.

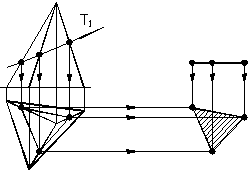
Рисунок 1.35 тАУ Перетин пiрамiди фронтально-проецiювальною площиною

Фiгура перерiзу конуса фронтально-проецiювальною площиною залежить вiд положення сiчноi площини вiдносно елементiв конуса. На рисунку 1.36 наведенi приклади побудови перерiзiв конуса фронтально-проецiювальними площинами.

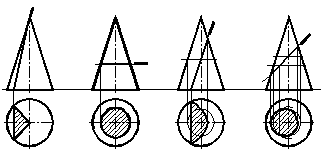
Рисунок 1.36 тАУ Перерiз конуса проецiювальними площинами

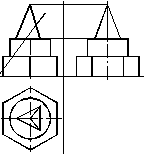
При виконаннi контурiв машинобудiвних креслень можливi варiанти, коли необхiдно побудувати перетин складного тiла проецiювальною площиною (рис. 1.37а) та визначити натуральну величину перерiзу. Пропоноване на рисунку 1.37а тiло складаiться iз послiдовно встановлених одну на одну шестигранноi призми, цилiндра та тригранноi пiрамiди.

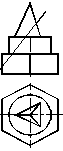
а) б)

Рисунок 1.37 тАУ Перерiз складного тiла фронтально-проецiювальною площиною

Для розвтАЩязання цiii задачi необхiдно перш за все побудувати профiльну проекцiю пропонованого тiла (рис. 1.37б) тАУ вигляд злiва.

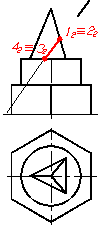
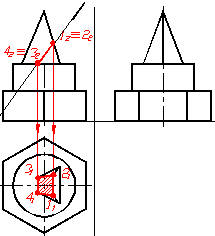
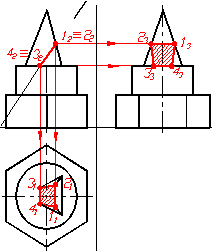
Перерiз пiрамiди фронтально-проецiювальною площиною тАУ чотирикутник 1234. Фронтальна проекцiя його тАУ це вiдрiзок, обмежений точками 1₂≡2₂ та 3₂≡4₂, який визначаiться без зайвих побудов. Горизонтальну та профiльну проекцii чотирикутника одержують по лiнiях проецiйного звтАЩязку, визначаючи точки на вiдповiдних елементах пiрамiди: точки 1 та 2 належать ребрам, а 3 та 4 тАУ основi пiрамiди. На рисунку 1.38а, б та в наведена поетапна побудова фiгури перерiзу пiрамiди заданою площиною.

а) б)

в)

Рисунок 1.38 тАУ Побудова проекцiй перерiзу пiрамiди фронтально-проецiювальною площиною

Перерiз цилiндра даною площиною тАУ елiпс, зрiзаний з двох сторiн прямими лiнiями, обмежений точками 5 тАУ 10. Фронтальна проекцiя фiгури перерiзу (рис. 1.39) тАУ вiдрiзок, обмежений точками 5₂ ≡ 6₂ та 9₂ ≡ 10₂. Горизонтальнi проекцii точок 5 тАУ 10 знаходять по лiнiях проецiйного звтАЩязку на горизонтальнiй проекцii цилiндра (коло). Профiльнi проекцii точок 5 тАУ 10 визначають по лiнiях проецiйного звтАЩязку (рис. 1.39), проведених iз точок 5₂≡6₂, 7₂≡8₂ та 9₂≡10₂. Вiдстань точок вiд осi симетрii вимiряють на горизонтальнiй площинi та вiдкладають на вiдповiднiй лiнiй проецiйного звтАЩязку. Шуканi профiльнi проекцii точок, належних фiгурi перерiзу, послiдовно зтАЩiднують плавною кривою лiнiiю.

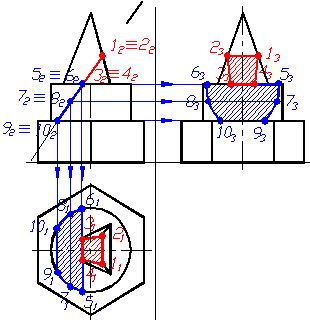
Рисунок 1.39 тАУ Побудова проекцiй перерiзу цилiндра фронтально-проецiювальною площиною

Фiгура перерiзу шестигранноi призми заданою фронтально-проецiювальною площиною тАУ чотирикутник, обмежений точками 11, 13, 14 та 12.

Фронтальна проекцiя фiгури перерiзу тАУ це пряма лiнiя, яка обмежена точками 11₂ ≡ 12₂ та 13₂ ≡ 14₂ (рис. 1.40).

Горизонтальнi проекцii точок 11, 12, 13 та 14 визначенi по лiнiях проекцiйного звтАЩязку в перетинi з контуром горизонтальноi проекцii шестигранноi призми (рис. 1.40).

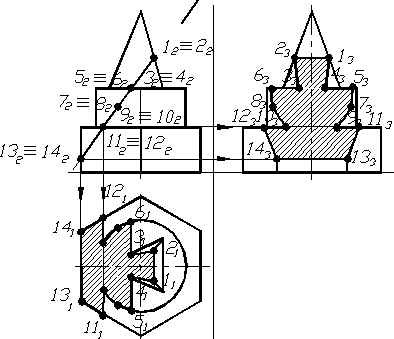
Рисунок. 1.40 тАУ Побудова проекцiй фiгури перерiзу призми фронтально-проецiювальною площиною

Профiльнi проекцii точок 11, 12, 13 та 14 одержують по лiнiях проецiйного звтАЩязку на вiдповiдних ребрах шестигранноi призми (рис. 1.40). Так, точки 11 та 12 належать верхнiй основi призми, а точки 13 та 14 тАУ бiчним ребрам. Для визначення профiльних проекцiй точок 13 та 14 достатньо з фронтальних проекцiй цих точок провести лiнii звтАЩязку до перетину з вiдповiдними ребрами. Для визначення положення профiльних проекцiй точок 11 та 12 необхiдно з фронтальноi проекцii iх (точка 11₂ ≡ 12₂) провести лiнii звтАЩязку, на яких вiдкласти вiдстанi, якi вимiряються на горизонтальнiй площинi проекцiй (на рисунку 1.40 це вiдстанi вiд горизонтальноi осi симетрii поверхнi вниз та вверх вiдповiдно до точок 13₁ та 14₁).

Натуральну величину фiгури перерiзу пропонованоi деталi заданою фронтально-проецiювальною площиною найпростiше визначити способом плоскопаралельного перемiщення (рис. 1.41). Для цього фронтальну проекцiю фiгури перерiзу тАУ пряму лiнiю разом з точками 1₂ тАУ 14₂, якi iй належать, розмiстити на вiльному мiсцi креслення паралельно осi х. Горизонтальнi проекцii нового положення точок 1 тАУ14 одержують в перетинi лiнiй проецiйного звтАЩязку, якi проведенi з нового положення фронтальноi проекцii фiгури перерiзу, з прямими, якi проведенi паралельно осi, з горизонтальних проекцiй точок 1 тАУ 14 (рис. 1.41).

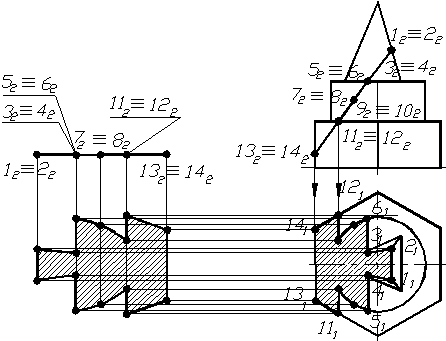
Рисунок 1.41 тАУ Визначення натуральноi величини фiгури перерiзу поверхнi фронтально-проецiювальною площиною

6. Побудова розгорток

У рiзних галузях технiки та будiвництва при виготовленнi виробiв з листового матерiалу часто мають справу з розгортками поверхонь.

Одержують цi розгортки за допомогою послiдовного сумiщення елементiв поверхнi з площиною.

6.1 Побудова розгортки пiрамiди

Щоб побудувати розгортку тригранноi пiрамiди, необхiдно перш за все визначити натуральнi величини ребер пiрамiди одним iз способiв перетворення комплексного креслення. Найпростiше це виконати способом плоскопаралельного перемiщення. Для цього на вiльному мiсцi креслення розмiстити, наприклад, горизонтальнi проекцii бiчних ребер так, щоб вони стали паралельнi осi Х. Зважаючи на те, що кожне ребро маi спiльну точку тАУ вершину S, зручнiше накладати одне ребро на iнше (рис. 1.42). Натуральну величину ребер одержують на фронтальнiй площинi проекцiй у перетинi лiнiй проецiйного звтАЩязку, якi проведенi з кiнцiв кожного ребра, з лiнiями, якi проведенi паралельно осi з кiнцiв фронтальних проекцiй ребер (рис. 1.42).

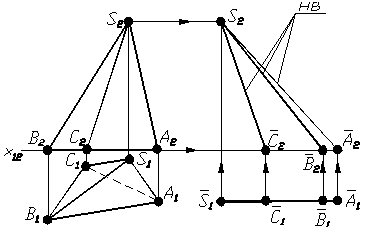
Рисунок 1.42 тАУ Визначення натуральноi величини ребер пiрамiди

Розгортку пiрамiди будують способом трiангуляцii. Для цього з довiльно вибраноi точки S провести промiнь, на якому вiдкласти натуральну величину будь-якого ребра (рис. 1.43а), наприклад, SA (натуральну величину вимiряють на фронтальнiй площинi проекцiй).

Для побудови гранi, наприклад ASB, необхiдно визначити положення точки В за двома заданими А та S (рис. 1.43б)). Точку В визначають у перетинi дуг, якi проведенi iз точок А та S та дорiвнюють натуральним величинам вiдповiдно до сторони основи АВ (вимiряються на горизонтальнiй площинi проекцiй, оскiльки основа паралельна горизонтальнiй площинi проекцiй) та бiчного ребра ВS, натуральна величина якого визначена на фронтальнiй площинi проекцiй.

а) б)

Рисунок 1.43 тАУ Побудова гранi SAB способом трiангуляцii

РЖншi двi гранi (SBC таSCA) бiчноi поверхнi пiрамiди будують так само, як грань ASB (рис. 1.44).

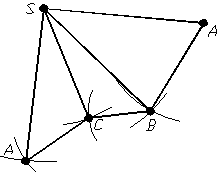
Рисунок 1.44 тАУ Розгортка бiчноi поверхнi пiрамiди

Для завершення побудови повноi розгортки пiрамiди необхiдно до будь-якоi гранi, наприклад до гранi ASB, добудувати трикутник основи (рис. 1.45).

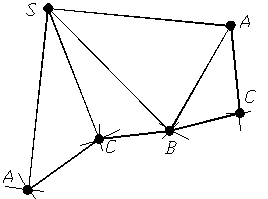
Рисунок 1.45 тАУ Повна розгортка пiрамiди

6.2 Розгортка призми

Розгортка поверхнi призми складаiться iз розгортки бiчноi поверхнi тАУ це прямокутники, кiлькiсть яких залежить вiд форми основи призми, та двох основ (рис. 1.46).

Рисунок 1.46 тАУ Розгортка призми

Кожний прямокутник маi розмiри сторiн: висота призми, натуральна величина якоi вимiряiться на фронтальнiй площинi проекцiй та вiдповiдну сторону основи, натуральна величина якоi вимiряiться на горизонтальнiй площинi проекцiй.

6.3 Розгортка цилiндра

Розгортка цилiндра складаiться з бiчноi поверхнi, яка i прямокутником, одна сторона якого дорiвнюi висотi цилiндра, а iнша тАУ довжинi кола основи цилiндра (2πR), та двох основ цилiндра тАУ кола радiусом R (рис. 1.47).

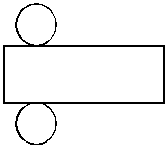
Рисунок 1.47 тАУ Розгортка цилiндра

При виконаннi розгортки цилiндра ii поверхню апроксимують призмою. Для цього коло основи подiляють на кiлька рiвних частин (наприклад, на вiсiм). Тодi при побудовi прямокутника бiчноi поверхнi на горизонтальнiй прямiй вiдкладають хорду кола стiльки разiв, на скiльки частин подiлене коло (рис. 1.48).

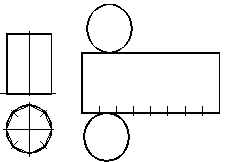
Рисунок 1.48 тАУ Побудова розгортки цилiндра

6.4 Розгортка конуса

Розгортка конуса складаiться з бiчноi поверхнi, що i сектором кола, радiус якого дорiвнюi твiрнiй, а кут визначаiться за формулою α = 360⁰R/l, та основи конуса.

При побудовi розгортки конуса ii поверхню найчастiше апроксимують поверхнею пiрамiди. Для цього основу подiляють на кiлька рiвних частин (на рисунку 1.49а тАУ на вiсiм).

Прямий конус маi однаковi твiрнi, натуральною величиною яких i твiрнi, що обмежують фронтальну проекцiю конуса (рис. 1.49а).

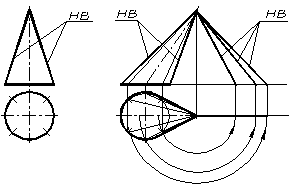
Нахилений конус маi рiзнi твiрнi. Натуральну величину мають твiрнi, що обмежують фронтальну проекцiю конуса. Натуральну величину всiх iнших твiрних визначають способом обертання навколо проецiювальноi осi (рис. 1.49б).

а) б)

Рисунок 1.49 тАУ Визначення натуральних величин твiрних конуса

Бiч

Вместе с этим смотрят:

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов