Аксонометричнi проекцii

Житомирський Вiйськовий РЖнститут

Нацiонального Авiацiйного Унiврситету

Реферат

на тему:

Аксонометричнi проекцii

Житомир 2010

План

1. Загальнi вiдомостi та основнi положення

2. Стандартнi види аксонометричних проекцiй. РЖзометрiя, диметрiя, способи iх побудови (осi, коефiцiiнти спотворень)

Загальний висновок

Лiтература

1. Загальнi вiдомостi та основнi положення

Креслення, якi виконанi методом ортогонального проекцiювання, мають ряд важливих особливостей, головною з яких i зручнiсть вимiрювання. В той же час для одержання уявлення про вирiб необхiдно розглядати декiлька виглядiв, часто доповнених перерiзами, розрiзами, додатковими i мiсцевими виглядами, виносними елементами. Все це ускладнюi на перших етапах вивчення креслення формування уявлення про вирiб.

У технiцi для наочного зображення виробiв або iх складових частин застосовуються аксонометричнi проекцii цих предметiв. Вони порiвняно з комплексним кресленням мають iстотну перевагу тАУ наочнiсть, але створюють незручностi при вимiрюваннi.

Слово ВлаксонометрiяВ» - грецьке. Воно складаiться з двох слiв: axon тАУ вiсь, metreo тАУ вимiрюю, що в перекладi означаi Влвимiрювання по осяхВ».

Побудова аксонометричних проекцiй допомагаi навчитися читати креслення i розвиваi просторове уявлення про форму предметiв i деталей.

Аксонометричнi проекцii застосовуються як допомiжнi до комплексних креслень у тих випадках, коли необхiдне пояснююче наочне зображення форми деталей.

Вiдмiннiсть аксонометричних проекцiй вiд ортогональних полягаi в тому, що в аксонометричнiй проекцii зображення предмета разом з осями координат одержуiться проекцiюванням паралельними променями на одну аксонометричну площину проекцiй.

На рис. 1 показана схема проекцiювання осей координат та вiднесеноi до них точки А на площину a. Направлення проекцiювання вказано стрiлкою S. Одержанi при такому проекцiюваннi аксонометричнi осi X', Y', Z' будуть проекцiями осей X, Y, Z комплексного креслення. О' тАФ аксонометрична проекцiя початку координат. Точка А' тАУ аксонометрична проекцiя точки А; точка А'₁ представляi собою аксонометричну проекцiю точки А₁. Якщо на кожнiй з координатних осей Х, У, Z (див. рис. 1) вiдкласти вiд точки О вiдрiзки е_х, е_у, е_z, довжини яких дорiвнюють одиницi натурального масштабу е, то внаслiдок проекцiювання одержимо е_Х, е_Y, е_Z тАФ аксонометричнi одиницi вимiру. В загальному випадку е_Х, е_Y, е_Zне рiвнi e та не рiвнi мiж собою.

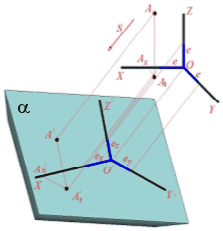
Вiдношення аксонометричноi одиницi вимiру е' до одиницi натурального масштабу е визначаi показник спотворення по аксонометричнiй вiсi.

Вiдношення довжини аксонометричноi проекцii вiдрiзка, розташованого вдовж визначеноi координатноi осi або паралельно до неi, до натуральноi довжини цього вiдрiзка, називаiться коефiцiiнтом спотворення.

Але при побудовi аксонометричних проекцiй звичайно користуються не самими коефiцiiнтами спотворення, а деякими величинами, iм пропорцiйними. Цi величини будемо називати приведеними коефiцiiнтами спотворення.

Вiдношення мiж аксонометричними проекцiями вiдрiзкiв, якi паралельнi осям координат X, Y, Z та самим вiдрiзкам рiвнi коефiцiiнтам

K_Х = е_Х /e, K_Y = е_Y /e, K_Z = e_Z /e.

Тому сутнiсть аксонометричного методу полягаi в тому, що обтАЩiкт вiдносять до прямокутноi системи координат та проекцiюють його разом з осями координат паралельними променями на деяку площину проекцiй, яку називають аксонометричною. Зображення, яке при цьому отримують, називають аксонометричним, а проекцii осей координат - аксонометричними осями координат.

Щоб побудувати аксонометрiю предмета, спочатку необхiдно вiднести його до системи трьох взаiмно перпендикулярних площин, що збiгаються з площинами проекцiй, вибрати площину i напрям проекцiювання, а потiм побудувати на основi паралельного проекцiювання за заданим напрямом на площинi проекцiю предмета разом з прямокутними координатними осями.

Зображення обтАЩiкта на аксонометричнiй площинi i напрям аксонометричних осей залежать вiд положення площини вiдносно системи координатних осей, а також вiд напряму проекцiювання.

Якщо напрям проекцiювання S перпендикулярний до площини проекцiй Р, то аксонометричнi проекцii називають прямокутними (j = 90В°). До прямокутних аксонометричних проекцiй вiдносяться iзометрична i диметрична.

Якщо напрям проекцiювання S не перпендикулярний до площини проекцiй a, то аксонометричнi проекцii називають косокутними (j ¹ 90В°). До косокутних аксонометричних проекцiй вiдносяться: фронтальна iзометрична, горизонтальна iзометрична i фронтальна диметрична проекцii.

Залежно вiд того, по скiлькох осях показники спотворення однаковi, визначають той чи iнший вид аксонометрii, а саме:

iзометрична проекцiя (iзометрiя) тАФ однаковi всi три показники спотворення (K_Х = K_Y = K_Z);

диметрична проекцiя (диметрiя) тАФ однаковi два з трьох показникiв

(K_Х тАФ K_Y ¹ K_Z; K_Х = K_Y ¹ K_Z; K_Х ¹ K_Y = K_Z);

триметрична проекцiя (триметрiя) тАФ показники рiзнi

(K_Х ¹ K_Y ¹ K_Z).

1. Сутнiсть аксонометричного методу полягаi в тому, що обтАЩiкт вiдносять до прямокутноi системи координат та проекцiюють його разом з осями координат паралельними променями на деяку площину проекцiй, яку називають аксонометричною. Зображення, яке при цьому отримують, називають аксонометричним, а проекцii осей координат - аксонометричними осями координат.

2. Вiдношення довжини аксонометричноi проекцii вiдрiзка, розташованого вдовж визначеноi координатноi осi або паралельно до неi, до натуральноi довжини цього вiдрiзка, називаiться коефiцiiнтом спотворення.

2. Стандартнi види аксонометричних проекцii. РЖзометрiя, диметрiя, способи iх побудови (осi, коефiцiiнти спотворень)

Найчастiше в кресленнi застосовуються прямокутнi аксонометричнi проекцii, оскiльки вони дають найбiльш наочнi зображення.

У табл. 1 наведено найменування видiв аксонометричних проекцiй, розташування iх осей i коефiцiiнти (показники) спотворення розмiрiв по осях.

СТАНДАРТНРЖ АКСОНОМЕТРИЧНРЖ ПРОЕКЦРЖРЗ

При цьому використовуються наведенi у таблицi коефiцiiнти спотворення: для iзометричних проекцiй K_Х = K_Y = K_Z= 1, для диметричних проекцiй K_Х = K_Z= 1; K_Y = 0,5.

При побудовi аксонометричних проекцiй користуються основною властивiстю аксонометрii (це - паралельнiсть проекцiй): якщо двi прямi паралельнi одна одноi в просторi, то вони паралельнi мiж собою в аксонометрii.

Побудова зображень не залежить вiд виду аксонометрii й полягаi в побудовi будь-якоi геометричноi фiгури за допомогою координат точок цiii фiгури. При цьому предмет маi розташовуватися так, щоб його було видно спереду, збоку i зверху.

Побудова геометричних фiгур в аксонометрii по заданих ортогональних проекцiях

Побудову аксонометрii починають iз призначення координатних осей в ортогональних проекцiях. Оскiльки поверхня предмета складаiться з лiнiй, а лiнiя з точок, то побудову аксонометричноi проекцii почнемо з точки. Перехiд вiд ортогональних проекцiй до аксонометричного зображення будують за алгоритмом:

1) на ортогональному кресленнi розмiчають осi координат;

2) будують аксонометричнi осi;

3) по характерних точках будують аксонометричне зображення.

Прямокутна iзометрична проекцiя. Нехай заданi ортогональнi проекцii точок А i В (рис. 2,а), то для побудови iзометричноi проекцii цих точок проводять аксонометричнi осi x', y', z' пiд кутом 120В° одна до одноi. Далi, вiд початку координат О' по осi О'x' вiдкладають вiдрiзок О'1' , що дорiвнюi координатi х точки В. Координату х беремо з комплексного креслення.

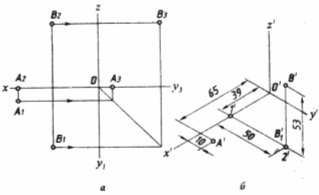
З точки 1' проводять пряму, паралельну осi y', i на нiй вiдкладають вiдрiзок 1'2', що дорiвнюi координатi y точки В; з точки 2' проводять пряму, паралельну осi z', на якiй вiдкладають вiдрiзок 2'В', котрий дорiвнюi координатi z точки В. Одержана точка В' тАУ шукана iзометрична проекцiя точки В.

Для побудови iзометричноi проекцii точки А достатньо двох координат х i y, так як третя координата z дорiвнюi нулю, оскiльки точка А лежить на площинi π₁ .

Аксонометричнi осi, а також вiдрiзки прямих, якi паралельнi осям, зручно будувати за допомогою креслярського трикутника з кутами 30В° та 60В° (рис. 2).

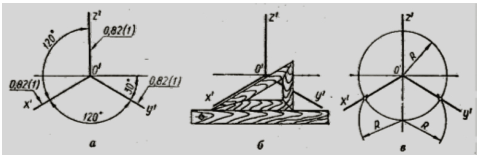
На рис. 2 показанi рiзнi прийоми побудови осей iзометрii: на рис. 2 ,б побудова здiйснена за допомогою трикутника з кутами 30, 60, 90В°; на рис. 2 ,в побудова здiйснена за допомогою циркуля.

На рис. 3 показанi рiзнi прийоми побудови осей диметрii: 1 тАУй спосiб - на рис. 3 ,б . На горизонтальнiй прямiй, яка проходить через точку О' вiдкладають по обидвi сторони вiд О' вiсiм рiвних довiльних вiдрiзкiв. З останнiх точок цих вiдрiзкiв вниз по вертикалi вiдкладають злiва один такий вiдрiзок, а з права тАУ сiм. Отриманi точки з'iднують з точкою О' та отримують аксонометричнi осi О' х' та О' у' .

2 тАУй спосiб - на рис. 3 ,в . На вертикальнiй прямiй вниз вiд точки О' вiдкладають вiдрiзок довiльноi довжини (О'D'), а вверх тАУ два таких же вiдрiзка (О'А'= 2 О'D' ). З точки О', як з центру проводять дугу кола радiусом R₁ = О' А' до перетину в точцi В' з дугою, проведеною з центру А' радiусом R₂ = А'D' . Пряма О'В' - направлення аксонометричноi осi х' . Третю дугу радiусом R₃ = В'А' проводять з центру В' до перетину з дугою радiуса R₂ в точцi С'. Пряма О'С' тАУ направлення аксонометричноi осi у' прямокутноi диметрii.

Найбiльш трудомiстким i побудова кiл. У прямокутних проекцiях коло, розташовано в площинах p₁, p₂, p₃, або iм паралельним, проекцiюiться в елiпси, причому бiльша вiсь елiпса перпендикулярна z, y, x вiдповiдно (див. табл. 1). Елiпси замiняються овалами, якi будуються по наведеним у таблицi значенням великих i малих осей (рис. 4,а). Слiд запамтАЩятати , що мала вiсь кожного елiпса завжди маi бути перпендикулярна до його великоi осi.

Для побудови кола користуються описаним навколо кола квадратом.

Чотирьом точкам торкання квадрата й кола (рис. 4,б) будуть вiдповiдати 4 точки торкання 1', 2', 3', 4' в аксонометрii (рис. 4,в). Ще чотири точки належать кiнцям великого й малого дiаметра елiпса (табл.1).

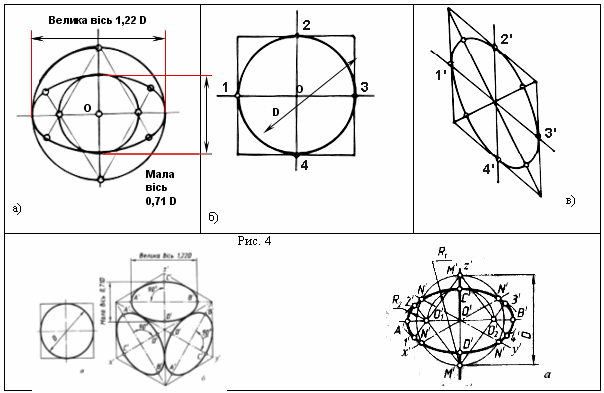
Для побудови овалу в площинi паралельнiй p₁ , проводять вертикальну i горизонтальну осi овалу. З точки перетину О' проводять допомiжне коло дiаметром D , що дорiвнюi дiйснiй величинi дiаметра зображуваного кола, i знаходять точки N' перетину цього кола з аксонометричними осями x' та y' . З точок М' перетину допомiжного кола з вiссю z', як з центрiв радiусом R₁= N'M' проводять двi дуги N'D'N' та N'С'N' кола, якi належать овалу.

З центра О' радiусом О'С', що дорiвнюi половинi малоi осi овалу, засiкають на великiй осi овалу А'В' точки О'₁ i О'₂. З цих точок радiусом R₂= О'₁1' = О'₁2' = О'₂3' = О'₂4' проводять двi дуги. Точки 1', 2', 3', 4' спряжень дуг радiусiв R₁ i R₂ знаходять зтАЩiднуючи точки M' з точками О'₁ i О'₂ та продовжуючи прямi до перетину з дугами N'D'N' та N'С'N.'

Таким же чином будують аксонометричнi проекцii геометричних тiл.

Приклад послiдовностi виконання аксонометричного зображення геометричного тiла.

Побудова аксонометрii обтАЩiмних фiгур. Необхiдно побудувати, наприклад, аксонометрiю правильноi призми з отвором за ii ортогональними проекцiями. Оскiльки основою призми i квадрат з вершинами на горизонтальних осях, то для забезпечення наочностi зображення доцiльно звернутися, наприклад, до прямокутноi диметрii.

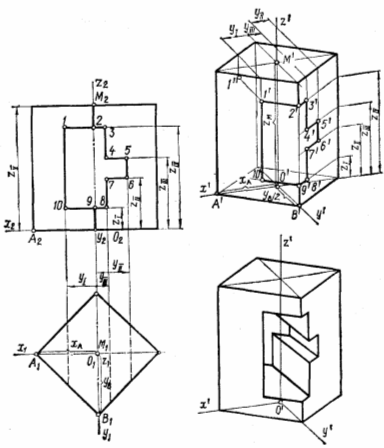
Побудову виконують у такiй послiдовностi.

1. Наносять ортогональнi осi на горизонтальнiй i фронтальнiй проекцiях, будують диметричну проекцiю осей.

2. Будують обтАЩiм призми в цiлому: спочатку точки А i В та симетричнi iм точки. Сполучивши iх, одержують аксонометрiю нижньоi основи. Вимiрюють висоту призми i вiдкладають цю величину уздовж осi аплiкат вiд точки О, визначивши точку М. Через точку М проводять аксонометричнi осi i будують верхню основу призми. Проводять вертикальнi ребра.