Формування математичних понять в процесi викладання математики в основнiй школi

ЗМРЖСТ

Вступ

Роздiл 1. Теоретичнi основи формування математичних понять

1.1. Поняття, як логiко-гносеологiчна категорiя

1.2. ОбтАЩiкт, поняття. Схожiсть iх i рiзниця

1.3. Суттiвi i несуттiвi властивостi понять. Прийоми iх виявлення

1.4. Змiст i обтАЩiм поняття. Зв'язок мiж ними

1.5. Види понять

1.6. Зв'язок мiж поняттями

1.7. Означення понять

1.8. Способи означення понять

1.9. Види означень

1.10. Структура означення

1.11. Основнi вимоги до означень

Роздiл 2. Основнi етапи розкриття змiсту математичного обтАЩiкта (формування означення)

2.1. Логiчний аналiз структури означення (видiлення термiна, роду, видових вiдмiнностей i логiчний зв'язок властивостей

2.2. Виконання дii пiдведення пiд поняття

2.3. Виконання дii виведення наслiдкiв

2.4. Абстрактно-дедуктивний та конкретно-iндуктивний методи навчання

Висновки

Список використаних джерел

ВСТУП

Актуальнiсть дослiдження. У математицi розглядаються рiзнi обтАЩiкти: числа, фiгури, формули, рiвняння та iншi. Усе це математичнi поняття. Щоб правильно органiзувати процес формування того чи iншого поняття в школi, треба насамперед чiтко визначити його змiст у науцi i його змiст у шкiльному курсi, памтАЩятаючи про те, що друге не повинне суперечити першому.

Виходячи з того в данiй роботi висвiтлене трактування того чи iншого поняття сучасною наукою, щоб забезпечити творчий пiдхiд до модифiкацii наукового означення для шкiльноi практики. Поняття тАУ це одна з основних форм мислення, в якiй вiдображаiться суть предметiв i явищ реального свiту в iх iстотних, необхiдних ознаках i вiдношеннях.

Отже, можна сказати, що поняття тАУ це цiлiсна сукупнiсть суджень про який-небудь обтАЩiкт, ядром якоi i судження, що вiдображають iстотнi ознаки обтАЩiкта.

ОбтАЩiкт дослiдження тАУ дiяльнiсть вчителя та учнiв на уроках математики в основнiй школi.

Предмет дослiдження тАУ методична система (змiст, обтАЩiм, види, способи, структура)формування математичних понять.

Мета дослiдження тАУ розробити й обТСрунтувати методику формування математичних понять в процесi викладання математики в основнiй школi.

Гiпотеза дослiдження тАУ розроблена методика формування математичних понять у процесi викладання математики в основнiй школi на основi освiтнього стандарту з математики сприятиме пiдвищенню якостi загальноосвiтньоi, математичноi, професiйноi пiдготовцi учнiв, розвиваi iнтуiцiю, деякi навики мислення, тобто сприяi пiдвищенню iх iнтелектуального рiвня.

Вiдповiдно до мети i гiпотези дослiдження було визначено такi завдання роботи:

В· аналiз психолого - педагогiчноi, методичноi, математичноi лiтератури з проблеми дослiдження;

В· розкрити загальнi питання формування математичних понять;

В· виявити психолого тАУ дидактичнi передумови застосування понять;

В· виявити психологiчнi закономiрностi процесу формування математичних понять в учнiв основноi школи.

Теоретичне значення результатiв дослiдження полягаi в розробцi методики формування математичних понять (змiст, обтАЩiм, види, способи, структура), яка враховуi особливостi навчальноi дiяльностi учнiв, операцiйний склад умiнь та психолого тАУ методичнi закономiрностi iх вироблення.

Практичне значення результатiв дослiдження:

тАФ розробленнi методичнi рекомендацii по формуванню математичних понять;

тАФ впроваджено методику вибору ефективних шляхiв, методiв та прийомiв формування математичних понять.

Джерелом дослiдження i науковi статтi з журналiв, методичнi посiбники та пiдручники з математики.

Апробацiя результатiв: одержанi результати поповнюють практичну базу методики викладання математики, а саме на тему: "Формування математичних понять в процесi викладання математики в основнiй школi".

Структура роботи. Випускна робота складаiться з двох роздiлiв. У першому роздiлi висвiтлюються теоретичнi основи формування математичних понять в основнiй школi. В другому роздiлi подаються основнi етапи розкриття змiсту математичного обтАЩiкта.

У кiнцi роботи додаiться список використаних джерел.

РОЗДРЖЛ РЖ. ТЕОРЕТИЧНРЖ ОСНОВИ ФОРМУВАННЯ МАТЕМАТИЧНИХ ПОНЯТЬ.

1.1. Поняття як логико-гносеологiчна категорiя

Що таке поняття? Питання здаiться тривiальним, оскiльки в повсякденному життi, в практичнiй роботi i в процесi навчання i дiтей, i студентiв всi ми оперуiмо тим або iншим термiном, не замислюючись над його змiстом, тобто поняттям, що позначаiться iм. Спiвбесiди iз студентами старших курсiв педагогiчних iнститутiв, з вчителями шкiл, молодими викладачами вузiв показали, що бiльшiсть з них не може розкрити змiсту термiну. РЖ не дивно, оскiльки нi в середнiй школi, нi у вищих учбових закладах в яких-небудь учбових курсах спецiально це питання не розглядаiться. Багато хто оперуi даним термiном, вважаючи змiст його саме собою розумiючим. Насправдi питання про iство поняття дуже складне. Немаi ще iдиноi думки серед фiлософiв, психологiв i логiкiв з питання про те, що ж таке поняття. Вiдомо бiльше 30 спроб дати визначення поняття. Великий угорський логiк Б.Фогарши в пiдручнику ВлЛогiкаВ» приводить 34 визначення поняття. Ф.Энгельс вiдзначав, що поняття тАФ це Влрезультати, в яких узагальнюються данi.. досвiдуВ», пiдсумки деякого етапу пiзнання.

Ряд логiкiв розглядаi поняття як форму мислення. Наприклад, логiк М.С. Строгович визначаi поняття як форму мислення, що вiдображаi i фiксуi iстотнi ознакиречей i явищ об'iктивноi дiйсностi. В.Ф.Асмус визначаi поняття як Влдумку про предмет, що видiляi в ньому iстотнi ознакиВ». С.Бакрадзе визначаi поняття як думку, що вiдображаi iстотнi ознаки предмету. Е.К.Войшвилло вiдзначаi, що таке визначення поняття дуже схожий з визначенням думки, тобто ознаки поняття як логiчнiй категорii i загальними з ознаками думки. Тому розглядати це визначення як тiльки те, що вiдображаi, iство поняття невiрне, i Е.К.Войшвилло даi своi визначення поняття.

По Е.К.Войшвилло, поняття i Влдумка, що i результатом узагальнення (i видiлення) предметiв або явищ того або iншого класу по бiльш менш iстотних (а тому i загальним для цих предметiв i в сукупностi специфiчним для них, видiляючи iх з безлiчi iнших предметiв i явищ) ознакахВ».

Мiж фiлософами i логiками йде суперечка, що первинне: думка або поняття? Що i бiльш високою формою мислення? Однi вважають, що початковi поняття, а думки i бiльш високою формою мислення. Це обгрунтовуiться тим, що думка складаiться з понять, виражаiться через зв'язанi мiж собою поняття. РЖншi, навпаки, вважають, що оскiльки саме поняття утворюiться в результатi думок i висновкiв i сам змiст понять розкриваiться за допомогою думок, те поняття тАФ вища форма мислення.

У ВлЛогiчному словнику-довiдникуВ» Н.И.Кондаков даi наступну характеристику поняття: ВлВищий ступiнь мислення досягаiться у формi поняття, яке i цiлiсна сукупнiсть думок, ядром якоi i думки про iстотнi ознаки, властивостi дослiджуваного об'iктуВ». Узагальнивши все, можна так охарактеризувати поняття. Поняття тАФ дуже складна логiчна i гносеологiчна категорiя. Це результат деякого етапу в розвитку наших знань про тi або iншi об'iкти матерiального миру. Виникнувши, поняття вже саме стаi об'iктом пiзнання. Разом з тим поняття тАФ одна з форм мислення i в цьому значеннi воно виступаi як знаряддя (засiб) пiзнання.

Наприклад, поняття молекули, виникнувши в науцi, зiграло величезну роль в пiзнаннi iства ряду явищ, на його основi була створена молекулярно-кiнетична теорiя. Це вiдноситься також до понять ВлелектронВ», ВлквантВ» i iн.

Мислення може протiкати в рiзних формах: понять, думок, висновкiв, гiпотез i теорiй. Всi вони грають величезну роль в пiзнаннi. Термiн ВлпоняттяВ» звичайно застосовуiться для позначення уявВнного образу деякого класу речей, процесiв, вiдношень об'iктивноi реальностi або нашоi свiдомостi. Математичнi поняття вiдображають в нашiй свiдомостi певнi форми i вiдношення матерiального свiту, абстрагованi вiд iх конкретних iндивiдуальних властивостей.

Кожне поняття поiднуi в собi клас об'iктiв (речей, вiдношень)тАФ обсяг цього поняття тАФ i характеристичну властивiсть, притаманну всiм об'iктам цього класу, i тiльки iм тАФ змiст цього поняття. НаприВнклад, поняття ВлтрикутникВ» поiднуi в собi клас найрiзноманiтнiших трикутникiв (обсяг цього поняття) i характеристичну властивiсть тАФ наявнiсть трьох сторiн, трьох вершин, трьох кутiв (змiст поняття); поняття ВлрiвнянняВ» поiднуi в собi клас всяких можливих рiвнянь (обсяг поняття) i характеристичну властивiсть тАФ рiвнiсть, яка маi одну або кiлька змiнних (змiст поняття.)Процес формування понять буде ефективним якщо вiн орiiнтуi учнiв на узагальнення i абстрагування iстотних ознак (характеристичВнноi властивостi) поняття, яке потрiбно сформувати.

Поняття тАФ одна з вищих форм мислення, форм вiддзеркалення матерiальноi дiйсностi. Але поняття не просте форма вiддзеркалення дiйсностi. Воно i такою формою вiддзеркалення, яка розкриваi iство речей, внутрiшнi, корiннi, визначаючi властивостi предметiв, iх внутрiшню суперечливу природу. Тому поняття i знання iстотних властивостей (сторiн) предметiв i явищ навколишньоi дiйсностi, знання iстотних зв'язкiв i вiдносин мiж ними.

По Гегелю, поняття тАФ перш за все синонiм дiйсного розумiння iстоти справи, а не простий вираз будь-якого загального в споглядаючих, вивчаються об'iктах. В поняттi розкриваiться справжня природа, особливiсть речi (об'iкту), а не ii зовнiшня схожiсть з iншими речами (об'iктами).

Як гносеологiчна категорiя поняття суперечливе. Воно i iднiсть протилежних моментiв, iднiсть загального i одиничного, конкретного i абстрактного. Вiдповiдно, процес засвоiння наукових понять також дуже складний i суперечливий. Наприклад, нескiнченнiсть множини рацiональних чисел, що знаВнходяться мiж будь-якими двома рацiональними числами, не ствердВнжуiться, а навпаки, ВлзаперечуiтьсяВ» конкретним сприйняттям скiнченого вiдрiзка, який вмiщуi цю множину.

Властивiсть щiльностi множини рацiональних чисел не можна виявити за допомогою дослiВнду, вона не пiдтверджуiться наочними геометричними уявленнями, а встановлюiться логiчно (абстрактно-дедуктивно). Цей та багато iнших прикладiв пiдтверджують висновки наших психологiв про те, що сприйняття наочного матерiалу через об'iктивнi особливостi цього матерiалу може вiдiгравати не лише позитивну, а й негативну роль.

1.2. ОбтАЩiкт, поняття. Схожiсть iх i рiзниця.

Поняття тАФ це одна з основних форм мислення, в якiй вiдображаiться суть предметiв i явищ реального свiту в iх iстотних, необхiдних ознаках i вiдношеннях.

Визначаючи поняття як одну з основних форм мислення, пiдкреслюють його роль та значення у пiзнаннi. Саме мисВнлення можна тодi розглядати як оперування поняттями, оскiльки перехiд вiд чуттiвих ступенiв пiзнання до абстрактВнного мислення характеризуiться як перехiд вiд вiдобраВнження свiту у формi вiдчуттiв, сприймань i уявлень до вiдображення його в поняттях i на iх основi,тАФ в судженнях i iнших логiчних категорiях.

Отже, можна сказати, що поняття тАФ це Влцiлiсна сукупВннiсть суджень про який-небудь об'iкт, ядром якоi i суВндження, що вiдображають iстотнi ознаки об'iктаВ».

Поняття виникають на основi суспiльноi практики i i продуктом багаторiчного iсторичного розвитку пiзнавальВнноi дiяльностi людини. Процес пiзнання здiйснюiться у формi чуттiвого пiВнзнання i в формi логiчного мислення.

Уявлення вiдрiзняються вiд понять тим, що вони виниВнкають у нашiй свiдомостi у виглядi наочних образiв, тодi як поняття тАФ це такi розумовi утворення, якi можуть таВнкож вiдображати i недостатнi органам чуття, закономiрнi вiдношення мiж предметами.

Поняття закрiплюi в системi знань змiст, загальний для всiх людей, незалежно вiд того, як та чи iнша людина уявляi собi цей предмет. На вiдмiну вiд уявлень, поняття позбавленi конкретноi наочностi, iх матерiальною оболонкою i слово. Поза словом-термiном поняття не можуть нi виникнути, нi iснувати.

Перша вiдмiнна риса поняття тАФ загальнiсть. На вiдмiну вiд чуттiвого пiзнання, поняття втiлюi в собi все баВнгатство конкретного одиничного i особливого. Чуттiвi образи показують здебiльшого одиничне, поняття вiдобраВнжаi загальне, що i в самiй дiйсностi. Поняття i могутнiшим засобом пiзнання, нiж форми чуттiвого пiзнання. ПраВнвильнi науковi абстракцii вiдображають дiйснiсть глибше, вiрнiше, повнiше, нiж живе споглядання.

Форма i змiст поняття як протилежностi складають iдине цiле. Логiчна форма тАФ це певний спосiб вiдображенВння предметiв, вiдображення однотипних зв'язкiв i вiдноВншень мiж предметами. Вона взагалi як структура думки являi собою завжди вiдношення в думках мiж протилежВнностями, тобто мiж окремим, особливим iзагальним, у лоВнгiчнiй формi поняття, судження i умовиводи мають рiзний характер. У формi поняття являi собою спiввiдношення мiж змiстом i об'iмом поняття. В формi судження тАФ це вiдношення мiж предметом думки i ознакою цього предмета. У формi умовиводу тАФ це також вiдношення мiж предметом думки i його ознакою.

Коли за змiстом поняття вiдображаi суть того чи iншого конкретного предмета або групи предметiв, то за своiю формою воно вiдображаi дещо загальне, iдине для рiзних предметiв i iх груп.

Поняття утворюiться в результатi абстрагування вiд iндивiдуальних властивостей предмета, воно вiдображаi сукупнiсть iстотних ознак предмета.

Розглядаючи множину об'iктiв, якi мають певнi спiльнi ознаки, ми вiдкидаiмо в уявi тi ознаки, якi належать окреВнмим, але не всiм об'iктам даноi множини, i фiксуiмо тi спiльнi ознаки, якi характернi всiм об'iктам даноi множини. Ця сукупнiсть спiльних ознак, якi вiдбивають приВнроду та iстотнi властивостi предметiв, визначаi поняття. Наприклад, щоб утворити поняття функцii, треба абстраВнгуватися вiд рiзних конкретних залежностей, що iснують у дiйсностi, i вибрати те спiльне, що iх об'iднуi, а саме: ту вiдповiднiсть мiж двома множинами, при якiй кожному елементу однiii множини вiдповiдаi один iдиний елемент другоi множини.

РЖстотну роль у формуваннi поняття вiдiграi мова. Поняття позначаiться словом, проте слово, що означаi поняття, зв'язане з чуттiвим досвiдом, в якому людина ознайомлюiться з самими предметами, що включаються в дане поняття.

У поняттi можуть вiдображатися i недоступнi органам чуття властивостi i вiдношення мiж предметами.

Можна, наприклад, мати поняття про велику кiлькiсть операцiй, що виконуi електронна лiчильна машина за сеВнкунду, але не уявляти собi швидкостi ii роботи.

З розвитком науки математичнi поняття формуються не лише на базi сприймань i уявлень (як початковi понятВнтя), а на базi вже ранiше встановлених понять.

Оволодiння будь-якою наукою немислиме без опануВнвання системи понять цiii науки. Це великою мiрою стоВнсуiться математики.

Найважливiшим завданням викладання математики i формування в учнiв правильних математичних понять.

1.3. Суттiвi i несуттiвi властивостi понять. Прийоми iх виявлення.

Засвоiння математичних понять вiдбуваiться у процесi аналiтико тАУ синтетичноi дiяльностi учнiв, спрямованоi на виявлення iстотних загальних властивостей певного поняття й усвiдомлення його неiстотних властивостей, а також на застосування нового поняття до розвтАЩязування задач. До пiзнавальноi дiяльностi учнiв щодо засвоiння математичних понять належать як загальнi (аналiз синтез, порiвняння, абстрагування, узагальнення тощо), так i специфiчнi розумовi дii (пiдведення до поняття i обернена iй дiя тАУ виведення наслiдкiв).

У разi використання абстрактно тАУ дедуктивного методу навчання для формування нового поняття вчитель формулюi означення сам, наводить приклади обтАЩiктiв, що належить до цього поняття, виявляi iстотнi спiльнi властивостi та зазначаi неiстотнi. Наприклад, запроваджуючи поняття Влтотожно рiвнi виразиВ» в 7 класi, вчитель маi сам сформулювати означення (два вирази, вiдповiднi значення яких рiвнi за будь-яких значень змiнних, називають тотожно рiвними) i навести приклади тотожно рiвних виразiв i таких, якi не i ними. Наприклад, вирази 3(x + y) i 3x + 3y, ab + 16c i 16c+ ab - тотожно рiвнi. Вирази 2x + y i 2xy тАУ нетотожно рiвнi. РЖстотною спiльною властивiстю тотожно рiвних виразiв i рiвнiсть iхнiх вiдповiдних числових значень за будь-яких однакових значень змiнних. Неiстотними ознаками i кiлькiсть змiнних, якi мiстить вираз, форма виразiв.

Наприклад, вираз 5(b+c) маi форму добутку, а тотожно рiвний йому вираз 5b+5c маi форму двочлена; тотожно рiвнi вирази ab + 16c i 16c+ ab рiзняться мiсцем одночленiв, що не i iстотним.

Труднощi засвоiння понять учнями, якi мають слабку пiдготовку, пояснюються передусiм невмiнням виокремлювати iстотнi властивостi обтАЩiктiв i абстрагуватись вiд неiстотних. У звтАЩязку з цим учнi роблять неправомiрнi узагальнення, iнакше кажучи, генералiзацiю неiстотних властивостей (надання iм ролi iстотних).РЖстотними для них стають яскравi властивостi, якi виявляються саме тодi, коли фiгури розмiщенi на рисунку стандартно.

1.4. Змiст i об'iм поняття. Зв'язок мiж ними.

Пiд змiстом поняття ми розумiiмо сукупнiсть усiх iстотних ознак, спiльних для всiх предметiв даного класу, що входять у дане поняття. Вчителю цi характеристики поняття потрiбно добре знати, щоб судити, як воно засвоiно, яким воно повинне бути.

Слiд зазначити, що однi й тi самi ознаки одного й того самого предмета i в одному випадку iстотними, а в iншому тАФ неiстотними. Все залежить вiд конкретного спiввiдношення зв'язкiв самого предмета i тих його ознак, якi в практичВнному вiдношеннi вважаються iстотними.

Об'iм поняття тАФ це сукупнiсть усiх предметiв, що охопВнлюються ним. Наприклад, до об'iму поняття Влдiйснi чисВнлаВ» входять множини рацiональних i iррацiональних чисел.

Змiст i об'iм поняття тiсно зв'язанi мiж собою i залеВнжать один вiд одного. РЖз збiльшенням змiсту поняття зменшуiться його об'iм i навпаки тАФ зменшення змiсту поняття збiльшуi його об'iм.

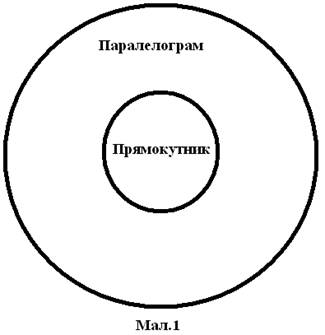
Наприклад, в об'iм поняття паралелограм входять всi види паралелограмiв; змiст цього поняття становлять ознаки: ВлчотирикутникВ» i Влпопарна паралельнiсть несумiжних сторiнВ». Коли до цих iстотних ознак додати ознаку Влконгруентнiсть усiх кутiв зазначеноi фiгуриВ», то об'iм поняття зменшиться, тепер до нього вхоВндить лише частина всiх паралелограмiв, тобто лише прямокутники.

Вiдношення об'iмiв двох зазначених понять можна графiчно подати у вигляВндi кругiв Ейлера (мал. 1).

Точки кожного круга зображають об'iкти класу, що належать даному поВнняттю. Великий круг зображаi поняття ВлпаралелограмВ», меншийтАФ поняття ВлпряВнмокутникВ».

Розподiл об'iму поняття. Певному родовому поняттю, як правило, вiдповiдають не одне видове поняття, а дещо. Так, поняттю Влелементарнi частинкиВ» вiдповiдають: електрон, нейтрон, фотон, позитрон, протон i т. д.; поняттю Вллистянi дереваВ» тАФ береза, клен, дуб, ясен, осика i т. д.; поняттю ВлпланетиВ» тАФ Земля, марс, Юпiтер i т.д.

Розумова операцiя, в результатi якоi розкриваiться об'iм родового поняття, тобто визначаються його види, називаiться в логiцi розподiлом об'iму поняття. Поняття, об'iм якого дiлиться, називаiться дiленим, а поняття, що виходять в результатi розподiли, називаються членами розподiлу. Розподiл об'iму поняття проводиться не довiльно, а на основi якоi-небудь ознаки, властивоi родовому i видовим поняттям. Ознака, по якiй проводиться розподiл об'iму родового поняття на види, називаiться пiдставою розподiлу.

Розподiл об'iму поняття необхiдно проводити на основi iстотних ознак. Залежно вiд пiдстави розподiлу родовi поняття можуть мити роздiленi на абсолютно рiзнi види.

При здiйсненнi операцii розподiлу об'iму поняття необхiдно слiдувати певним правилам:

1. Члени розподiлу (видовi поняття) повиннi виключати один одного, тобто кожний предмет входить в об'iм тiльки одного видового поняття.

2. При одному i тому ж розподiлi потрiбно користуватися однiiю пiдставою розподiлу.

Наприклад, родове поняття ВлробiтникВ» по пiдставi ВлпрофесiяВ» дiлиться на наступнi види: ВлслюсарВ», ВлтокарВ», ВлковальВ» i т. д., а по ознацi ВлосвiтаВ» тАФ що Влзакiнчив 10 класiвВ», що Влзакiнчив 8 класiвВ» i т.д.

Будь-яке поняття можна роздiлити по рiзних пiдставах, але у кожному окремому випадку розподiли поняття повинна витримуватися одна ознака як пiдстава розподiлу.

Приклади розподiлу по рiзних ознаках поняття ВлчислоВ»:

Ва1) позитивне i негативне;

Ва2) цiле i дробове;

Ва3) просте i складове;

4) iменоване i вiдвернуте;

5) парне i непарне;

6) рацiональне i iррацiональне;

7) уявне i дiйсне.

Вибiр тiii або iншоi пiдстави в кожному розподiлi визначаiться цiлями, якi ставить людина в процесi вивчення предметiв матерiального миру. В учбовiй практицi досить часто допускаiться розподiл вiдразу по декiлькох пiдставах. Так, учнi (а деколи i самi вчителi), перераховуючи види руху, називають: вертикальний рух, вiльний рух, прямолiнiйний, криволiнiйний i т. д., а перераховуючи на уроках геометрii трикутники, розташовують в один ряд: рiвнобедренi, гострокутнi, прямокутнi, подiбнi.

3.ВаВаВаВаВа Члени розподiлу (видовi поняття) повиннi бути найближчими видовими поняттями даного родового, iнакше кажучи, розподiл повинен бути безперервним, не перескакувати через види, а переходити вiд роду до його найближчих видiв.

Наприклад, до листяних дерев вiдносяться береза, дуб, липа, осика i т.д. Але не можна говорити, що лiс буваi листяна, змiшана, берези, осики, сосни i т.д. невiрний розподiл типу: ВлТварини тАФ кiшка, собака, верблюд, слон, бегемот i т.д.В». Вiрно: ВлТварини тАФ хижi i нехижi, дикi i домашнi i т. д.В».

Порушення цього правила називаiться стрибком в розподiлi. Прикладом подiбноi помилки i наступний розподiл:

ВлНебесне тiло тАФ зiрка, планета, ЗемляВ». ВлНебесне тiлоВ» не i найближчим родом для поняття ВлЗемляВ». Для поняття ВлЗемляВ» найближчий рiд тАФ ВлПланетаВ». Вiдношення об'iмiв даних понять можна зобразити схемою, представленою на мал. 2.

4. Розподiл повинен бути вiдповiдним, тобто сума об'iмiв видових понять повинна дорiвнювати об'iму дiленого родового поняття. При порушеннi цього правила припускаiться двох помилки: помилка вузького розподiлу об'iму поняття i помилка широкого розподiлу об'iму поняття. Розкриiмо змiст цих помилок докладнiше:

а) вузький розподiл об'iму поняття. Суть цiii помилки в тому, що при розподiлi родового поняття перераховуються не всi види, що входять в його об'iм, тобто сума об'iмiв видових понять менше об'iму дiленого поняття. Наприклад, перераховуючи основнi характеристики елементарних частинок, називають тiльки заряд i спин. Перераховуючи види газових розрядiв, називають тiльки iскровою, дуговий i коронний, але не указують тлiючий розряд. В поняття внутрiшньоi енергii учнi включають тiльки кiнетичну i потенцiйну, енергiю взаiмодii молекул (не включають енергiю зв'язку електронних оболонок, внутрiядерну, енергiю гравiтацiйноi взаiмодii частинок i iн.);

б) широкий розподiл об'iму поняття. При широкому розподiлi вводять такi види, якi не мiстяться в об'iмi дiленого поняття, тобто сума об'iмiв видових понять бiльше об'iму родового поняття. Наприклад, перераховуючи основнi одиницi вимiрювання фiзичних величин в системi СРЖ в механiцi, учень назвав метр, кiлограм, ампер, ньютон, джоуль i секунду. Але ампер, ньютон i джоуль не мiстяться в об'iмi вказаного поняття. Ампер тАФ одна з основних одиниць вимiрювання в системi СРЖ, але не в механiцi, а джоуль i ньютон тАФ похiднi одиницi. З погляду операцii порiвняння всi поняття в логiцi справВ» на порiвняннi i незрiвняннi. Порiвнянними називаються поняття, що мають яку-небудь загальну ознаку. Загальним бiля порiвнянних понять i родове поняття (родова ознака), в об'iм якого вони входять.

Незрiвнянними називаються поняття, якi неможливо порiвняти нi за об'iмом, нi за змiстом. Незрiвняннi поняття: не мають загального роду, i iх змiст iстотно рiзний. Наприклад: ВлстiлВ» i ВлверблюдВ», ВлсоловейВ» i ВлолiвецьВ».

Разом з тим необхiдно вiдзначити: не можна вважати, що iснують незрiвняннi поняття взагалi. Як би два поняття не були рiзними i за змiстом, i за об'iмом, вони можуть бути порiвняннi. Як вже було сказано вище, кожне поняття пов'язано зi всiма iншими.

По характеру вiдносин порiвняннi поняття дiляться на двi; групи: сумiснi i несумiснi.

Сумiсними називаються поняття, що мають загальне найближче родове поняття (родова ознака).

ВаРЗх видовi ознаки спiвпадають частково або повнiстю. Звiдси витiкаi, що об'iми сумiсних понять можуть спiвпадати частково.

1.5. Види понять.

У шкiльному курсi математики вивчають три види понять:

1) первiснi (неозначуванi);

Ва2)означуванi;

3) поняття, якi вводяться описуванням, на прикладах.

ВаВ останньому випадку учнi частково дiстають уявлення про iстотнi властивостi поняття, але означення поняття не формулюiться з дидактичних мiркувань. Розглянемо особливостi методики формування трьох основних видiв понять.

Первiснi поняття. На перших уроках геометрii в 7 класi розкриваються iстотнi властивостi понять ВлточкаВ» i ВлпрямаВ» за допомогою системи аксiом планiметрii. Тут учнiв ознайомлюють з важливими вiдношеннями ВлналежатиВ» для точок i прямих, Вллежить мiжВ» - для трьох точок прямоi. Доцiльно звернути увагу учнiв на те, що поняття точки, прямоi, площини походять вiд реальних iснуючих об'iктiв довкiлля.

Наприклад, уявлення про пряму даi натягнута нитка, дрiт, уявлення про точку - мiсце дотику олiвця до паперу чи крейди до дошки, уявлення про площину тАУ поверхня озера. Проте в геометрii цi фiгури дiстають, нехтуючи такими властивостями, як розмiри точки, товщина прямоi, площини. Пряма в геометрii не маi товщини i уявляiться продовженою необмежено, хоча зображаiться у виглядi вiдрiзка.

Пiд час формування первiсних понять геометрii важливо, щоб учнi добре засвоiли термiнологiю стосовно цих понять. Наприклад: Влточки А i С лежать на прямiй аВ», або Влточки А i С належать прямiй аВ»; Влпрямi а i b перетинаються в точцi СВ», або Влточка С i точкою перетину прямих а i bВ».

Учнi мають усвiдомити, що поняття Вллежить мiжВ» стосуiться точок прямоi. Доцiльно не тiльки ввести поняття i проiлюструвати на рисунку, а й розв'язати кiлька вправ на пiдведення до цього поняття. Зокрема, можна запропонувати учням указати точки, якi лежать мiж двома iншими точками. В цьому разi доцiльно взяти не тiльки точки прямоi, а й точки довiльних лiнiй, наприклад кола, ламаноi (Мал.3).

Якщо запропонувати учням позначити точку К, яка лежить мiж даними точками А i В прямоi, то деякi учнi можуть поставити точку К посерединi вiдрiзка АВ. Це повтАЩязано з розумiнням цього поняття в життiвiй практицi. Учням слiд пояснити: в геометрii точкою, що лежить мiж точками А i В, i не лише середина вiдрiзка АВ, а будь тАУ яка точка вiдрiзка, розмiщена правiше вiд А i лiвiше вiд В.

Дехто з учнiв може назвати точку С кола такою, яка лежить мiж точками А i D цього кола. Учнi мають умiти обТСрунтовувати неправильнiсть такоi вiдповiдi, розрiзняти сформоване на життiвому досвiдi поняття Вллежати мiжВ» i наукове, геометричне поняття.

Означуванi поняття. У систематичних курсах алгебри i геометрii значна кiлькiсть нових понять означаiться. Наприклад, тотожно рiвнi вирази, тотожнiсть, тотожне перетворення виразiв, корiнь рiвняння, лiнiйне рiвняння з одним невiдомим, функцiя, багаточлен, степiнь багаточлена, вiдрiзок, промiнь, коло, трикутник, паралельнi прямi в просторi, багатогранник.

Вводячи означення математичних понять, потрiбно враховувати, наскiльки вiдомi й зрозумiлi учневi певного вiку тi iстотнi властивостi, якi розкривають змiст нового поняття. Психолог Дж. Брунер з цього приводу зазначав, що коли основнi поняття подано у формальному виглядi як рiвняння або точнi словеснi означення, то вони i недоступними для дитини, якщо вона не засвоiла iх спочатку iнтуiтивно.

Це зауваження стосуiться введення означень на всiх етапах навчання. Що абстрактнiше поняття, складнiша логiчна структура його означення, то гострiша потреба в попередньому запровадженнi поняття на iнтуiтивному рiвнi, у поясненнi властивостей, якi увiйдуть в означення, спочатку на конкретних прикладах з використанням наочних образiв. Важливо звертати увагу школярiв на логiчну структуру означень i передусiм чiтко називати спiльнi iстотнi властивостi, що входять в означення, характер iх зв'язку (кон'юнктивний, диз'юнктивний чи обидва одночасно). При цьому не обов'язково вводити термiнологiю логiки, важливо пояснити роль сполучникiв.

Пiд час пiдсумкового повторення в 9 класi або на перших уроках стереометрii, коли пояснюiться логiчна будова геометрii, слiд звернути увагу учнiв на принципову можливiсть рiзних означень того самого поняття залежно вiд вибору iстотних властивостей, що мiстить означення. Це можна пояснити на прикладi паралелограма. Водночас не можна допускати, щоб в учнiв склалося уявлення про довiльнiсть введення математичних понять взагалi та iх означень зокрема.

Потрiбно показати учням приклади обТСрунтування доцiльностi введення саме такого, а не iншого означення певного поняття. Наприклад, пiд час розгляду поняття степеня з нульовим i вiд'iмним показниками слiд пояснити, що доцiльнiсть запропонованих означень спричинена потребою поширити правила дiй над степенями з натуральним показником на степенi з нульовим i цiлим вiд'iмним показниками.

Поняття, що вводяться описово.Значна кiлькiсть математичних понять, що вивчаiться в курсах математики початковоi школи та 5 тАФ6 класiв, вводиться описово. Наприклад, у 5 класi за посiбниками так вводять поняття числового й буквеного виразiв, вiдрiзка, кута, трикутника, площi, звичайного дробу, десяткового дробу, прямокутного паралелепiпеда; у 6 класi тАФ поняття простого i складеного чисел, кола, кругового сектора, кулi, вiд'iмного числа, додатного числа, числовоi прямоi, прямокутноi системи координат, коефiцiiнта, подiбних доданкiв.

Низка понять вводиться описово, на прикладах i в систематичних курсах алгебри, геометрii. Наприклад, у 7 класi на уроках алгебри на кiлькох прикладах запроваджуiться поняття одночлена i його стандартного вигляду. При цьому увагу звертають на те, що наведенi вирази i добутком чисел, змiнних та iхнiх степенiв, тобто фактично розкривають iстотну властивiсть одночленiв. Розглядаючи поняття Влгеометрична фiгураВ» на першому уроцi геометрii в 7 класi, недоцiльно обмежуватися лише рисунками фiгур, запропонованих у пiдручнику.

ВаПотрiбно показати учням моделi рiзних планiметричних фiгур i геометричних тiл, наприклад трикутникiв, виготовлених з дроту, i плоских трикутникiв, вирiзаних з паперу або картону, кола, круга, паралелепiпеда, кулi. Слiд звернути увагу на те, що обидва трикутники, коло, круг можуть розмiститися в площинi всiма своiми точками, а паралелепiпед i куля тАФ нi. Цi першi уявлення про особливостi рiзних геометричних фiгур сприятимуть свiдомому засвоiнню iхнiх властивостей у подальшому вивченнi курсу геометрii.

У процесi формування математичних понять учнi припускаються помилок, самостiйно виявляючи iстотнi властивостi у разi формування поняття конкретно-iндуктивним методом i формулюючи означення, якщо iх уже введено. При цьому учнi часто не помiчають деяких iстотних властивостей або умов, невдало вибирають або взагалi пропускають родове поняття.

Найефективнiше названi помилки виправляти за допомогою контрприкладiв, якi допомагають не тiльки краще усвiдомити iстотнi властивостi понять, а й мiцнiше запам'ятати iх.

Наведемо приклад застосування контрприкладiв для виправлення помилок учнiв пiд час формулювання вже наведених ранiше означень понять.

На уроках геометрii учнi вже ознайомились з означенням хорди. Пiд час повторення вивченого було допущено помилку в означеннi. При цьому ВлдiалогВ» учителя з учнем може бути таким.

Учень. Хорда тАФ це лiнiя, що з'iднуi двi точки кола.

Учитель проводить хвилясту лiнiю, що з'iднуi двi точка кола.

Учень. Хорда тАФ це пряма лiнiя, що з'iднуi двi точки кола.

Учитель проводить сiчну, що проходить через центр кола.

Учень. Хордою називаiться вiдрiзок, що з'iднуi двi точки кола.

Рiвнозначнi поняття. Вiдношення рiвнозначностi (або тотожнiсть) утворюiться мiж поняттями, що вiдображають один i той же предмет, його зв'язки.

У кожному предметi i, з одного боку, iстотнi ознаки, що i загальними для класу предметiв, з iншою специфiчнi, характернi для даного предмету. Загальнi ознаки, як вже мовилося, i родовими ознаками, специфiчнi тАФ видовими. Родова ознака в даному випадку як би зв'язуюча ланка мiж видовими поняттями.

У видових ознаках тотожних понять вiдображаються рiзнi сторони одного i того ж предмету або явища. Значить, видовi ознаки цих понять не виключають, а доповнюють один одного. Звiдси витiкаi, що об'iми тотожних понять спiвпадають.

Виходячи зi всього сказаного можна дати наступне визначення рiвнозначних (тотожних) понять.

Рiвнозначнi поняття тАФ це сумiснi поняття про один i той же предмет i вiдмiннi по видових ознаках, що характеризують рiзнi сторони даного предмету:

Дуже важливо умiло користуватися рiвнозначними поняттями в практичнiй дiяльностi. Умiле iх використовування при викладi учбового матерiалу, при читаннi лекцiй, виступiв з докладом робить iх цiкавими за формою i змiстом, не стомлюi одноманiтнiстю. Цьому умiнню потрiбно навчати дiтей з найперших днiв в школi.

Необхiдно звернути увагу на помилки, що припускаiться деколи, при операцii рiвнозначними поняттями. Так, часто учнi ототожнюють абсолютно нерiвнозначнi поняття. Наприклад, па уроках математики помилково ототожнюються такi поняття, як ВлкругВ» i ВлколоВ», Влдодати нульВ» i Влприписати нульВ»; на уроках хiмii ототожнюються такi поняття, як безбарвнийВ» i ВлпрозорийВ», ВлбезбарвнийВ» i ВлбiлийВ»; на уроках фiзики часто спостерiгаiться ототожнення понять Влсила тяжкостiВ» i Влвага тiлаВ», Влсила тискуВ» i ВлтискВ», ВлсилаВ» i ВленергiяВ» ВлсилаВ» i ВлпотужнiстьВ».

Поняття, що перехрещуються (вiдношення перетину). Поняттями, що перехрещуються, називаються видовi поняття, що мають загальний рiд, а видовi ознаки кожного з них вiдображають як специфiчнi, так i частково загальнi сторони (властивостi) предметiв i явищ.

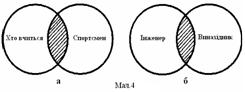
Частковий збiг видових ознак понять, що перехрещуються, обумовлюi частковий збiг iх об'iмiв. Таким чином, на вiдмiну вiд рiвнозначних понять, де видовi ознаки не пов'язанi один з одним i вiдображають рiзнi сторони предмету, в поняттях, що перехрещуються, видовi ознаки частково спiвпадають. Приклади понять, що перехрещуються: що ВлвчитьсяВ» i ВлспортсменВ», ВлiнженерВ» i ВлвинахiдникВ». В приведених прикладах загальним родовим поняттям i ВллюдинаВ». Частина видових ознак поняття що Влвчиться входить в змiст поняття ВлспортсменВ»тАФ деякi спортсмени можуть бути тими, що вчаться, але не обов'язково все, i, навпаки, частина видових ознак поняття ВлспортсменВ» складаi певну частку змiсту поняття що ВлвчитьсяВ» тАФ деякi учнi можуть бути спортсменами. Спiввiдношення понять ВлiнженерВ» i ВлвинахiдникВ» таке ж. Значить, об'iми цих понять частково спiвпадають. Наочно це вiдношення зображаiться за допомогою двох кругiв, що перехрещуються, як показано на мал. 4 (а, б).

Приклад понять, що перехрещуються: ВлрiдинаВ» i ВлводаВ». Вода може бути в рiдкому, газоподiбному i твердому поляганнях. Тiльки частина води може знаходитися в рiдкому поляганнi. Так само тiльки частину рiдини може складати вода. Загальним родовим поняттям для даних понять i ВлречовинаВ».

Утворити поняття, що перехрещуються, можна при розподiлi якого-небудь родового поняття по рiзних пiдставах. Одержанi видовi поняття знаходитимуться вiдносно часткового збiгу. Наприклад, поняття ВллюдинаВ» роздiлимо по двох пiдставах: ВлнацiональнiстьВ» i Влколiр волоссяВ». Одержимо двi групи видових понять, що знаходяться мiж собою вiдносно часткового збiгу: ВлросiйськийВ», ВлукраiнецьВ», ВлгрузинВ», ВлказахВ» i т. д.; ВлбрюнетВ», ВлблондинВ» i т.д. Цi поняття не будуть рядоположными. Щодо понять, що перехрещуються, в

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики