Численные методы

ЛЕКЦИЯ №5

МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

СНУ

Пусть дана система вида:

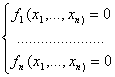ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.1)

f'(x)=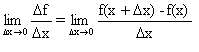Ва- производная

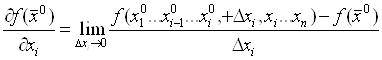
Частная производная 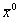- вектор (все значения).

МЕТОД НЬЮТОНА

Дана система вида (5.1), где f_i один раз непрерывно дифиринцируемые функции, т.е. существуют все частные первые производные этих функций.

Строим последовательность приближений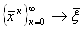Васходящуюся к точному решению системы .

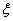ВаПусть 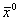Ва- некотороеВа начальное приближение к решению, а 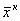- катое приближение к решению. Построим зависимость, позволяющую на основании 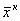Вапостроить .

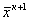Точное приближение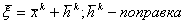

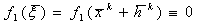
ξ-корень обращает уравнение в верное равенство(тождество).

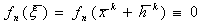ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.2)

Разложим функции f_i из системы (5.2) в ряд Тейлора в окрестности точки х^к до линейных составляющих.

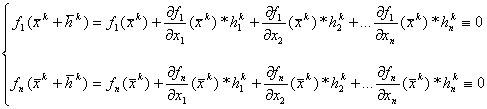ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.3)

Система (5.3) представляет собой систему линейных алгебраических уравнений для поиска компонента вектора поправки h^k.

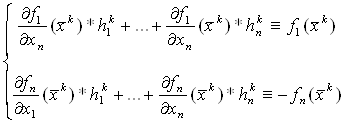
Перепишем систему (5.3) в виде:

ВаВа (5.4)

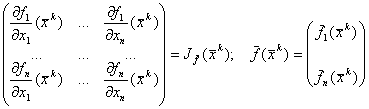
Сокращаем запись системы (5.4) : 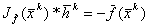ВаВаВаВа(5.5)

Решим систему (5.5) методом обратной матрицы. Определитель Якобиана в точке х^к не равен 0.

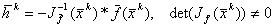
Получили связь последующего приближения с предыдущим.

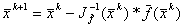ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.6)ВаВаВаВаВаВа

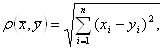
условие окончания вычислений.Ва (5.7)

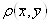- расстояние между векторами (метрика).

МЕТОД ИТЕРАЦИЙ

Пусть дана система вида (5.1). Преобразуем ее к видуВаВа (5.8)

Система (5.8) в векторном виде 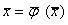ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(5.9)

Необходимо найти неподвижную точку систему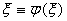

Очевидно, что эта точка ξ тАУ решение системы (5.1)

Пусть дано 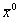-некоторое начальное приближение к ξ и на k-том шаге получено приближение 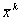. Тогда последующее приближение :

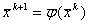ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.10)

Условие окончания совпадает с (5.7)

Всегда ли метод сходится?

Пусть М- матрица, составлена из элементов m_ij

M=[m_ij], где m_ij=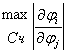

Определение нормы матрицы А: -число удовлетворяющее свойствам.

1) ≥0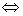, =0≡0

2) 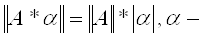число

3)

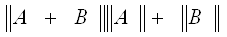
4)

Способы задания нормы матрицы:

1) =

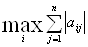
2) =

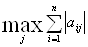
3) =

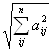
Достаточное условие сходимости метода итераций:

Если 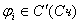, i=1,nВа , 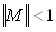на Сч и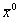 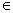Сч, то процесс итераций сходится независимо от выбора начального приближения.

МЕТОД ЗЕЙДЕЛЯ

Пусть дана система вида (5.1), преобразуем ее к виду (5.8). Как и в методе итераций строим последовательность приближений 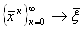Вак неподвижной точке.

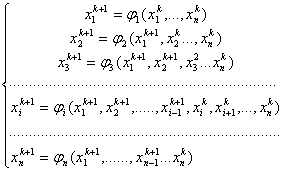
Ваускорение сходимости за счет подстановки предыдущего приближения.

Достаточное условие совпадает с достаточными условиями сходимости метода итераций.

Условие окончания получения приближений совпадает с (5.7).

ЛЕКЦИЯ № 6, 7

ПРИБЛИЖЕНИЕ ФУНКЦИИ

Общая постановка задачи.

Пусть Вж(c) тАУ некоторая функция, которая может быть известно, частично известной и неизвестной. Эту функцию необходимо заменить некоторой ВлхорошейВ» функцией j(c), которая будет достаточно близкой Вж(c).

Постановка задачи интерполяции.

Для того чтобы конкретизировать постановку задачи приближения функции необходимо ответить на следующие вопросы:

1. что известно о Вж(c) (способ задания, степень гладкости);

2. к какому классу, семейству функций должна принадлежать j(c);

3. что понимаем под близостью j(c) и Вж(c) каков критерий согласия;

Часто приближение функции называют аппроксимацией

Постановка задачи интерполяции.

Пусть Вж(c) задана на некотором разбиении отрезка [a;b] точками х_i,

i=0,n , где a = х₀<х₁<тАжn= b

интерполяция тАУ вычисление Вж(c) в точке Î[a;b],Ва x ¹ x_i,Ва i = 0,n

экстраполяция тАУ вычисление функции Вж(c) в точке ХÎ[a;b];

Определение интерполяции ввел в 1656 году Джон Уолесс, а в 1655 году ввел символ ¥.

Для полиномиальной интерполяции j(c) имеет вид j(c)=а₀+а₁х+а₂х²+тАж+а_nxⁿ.

Для того, чтобы считать j(c) к Вж(c) вводится ограничение j(c_i)= Вж(c_i), i=0,n ;

Т.еВа значения этих функций в точке х_i должны совпадать. Точки х_iВабудем называть узлами интерполяции

Интерполяционный многочлен Лагранжа

Необходимо определитьВа коэффициенты полинома степени n(их будет n+1), построения аппроксимации функции, заданной в n+1 узле. Используя ограничения на j(c): j(c_i)= Вж(c_i)=y, i=0,n , составим систему:

(6_.1)

Выпишем определитель этой системы

Определитель

Вандермонда

При условии: x₀¹x_jприВаi¹j определитель системы (6.1) отличен от нуля, следовательно, система имеет единственное решение.

Вывод:

если задано разбиение в виде n+1различной точки, то всегда существует функция в виде полинома n-ой степени, которая проходит через все точки графика Вж(c),определенной на этом разбиении.

Посторонние приближенияфункции при помощи полиномов указанным способом весьма трудоемко и обладает большой вычислительной погрешностью, поэтому его использование для большого числа узлов интерполяции нецелесообразно.

Лагранж предложил строить интерполяционные полиномы в виде:

P_n(x)=∑ C_i l_i(x) ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(6.2)

C_i=y_i=Вж(c_i), l_i(x)=полиномы n-ой степени, которые удовлетворяют условию:

Для полинома узлы интерполяции x_j, j=0,n , j≠I являются корнями, причем действительными и попарно различными (все имеют кратность 1)

Тогда полином l_iможет быть записан в виде:

ВаВаВаВа (6.3)

Общий вид полинома Лагранжа:

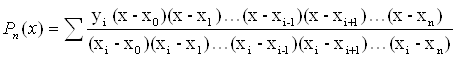ВаВаВаВаВаВа (6.4)

Встает вопрос о точности,Ва о приближения функции. Вводится понятие остаточного членаВа многочлена Лагранжа ; для того, чтобы оценить аппроксимацииВа Вж(c) в некоторой точкеВаВа x Î[a;b]

Функцию Вж(c)Ва представим в виде Вж(c)= P_n(x)+R_n(x), где R_n(x)- остаточный член многочлена Лагранжа в процессе длительного и трудоемкого вывода для R_n(x) получена следующая формула:

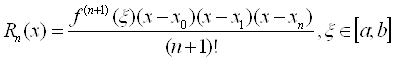ВаВаВа Ва ВаВаВаВаВаВаВа(6.5)

Строится система вложенных отрезков

Вж⁽ⁿ⁺¹⁾ -производная (n+1)-го порядка

ПустьВа

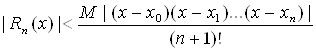ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.6)

Если Вж(c)-полином n-ой степени, то производная (n+1)-го порядка равна 0, тогда R_n(x)≡0 и мы получаем точную аппроксимацию.

Теорема:

Многочлен Лагранжа вида (6.4) для таблично заданной функцииВа единственен.

Доказательство:

Пусть Q_n(x)- многочлен Лагранжа, построенный для этой же функции Вж(c) по тем же узлам интерполяции. Q_n(x) ¹P_n(x)Ва Q_n(x_i)=y_i=P_n(x_i),

Рассмотрим многочлен L_n(x)= Q_n(x)-R_n(x)-это многочлен n-ой степени, для которого точки x_i, i=0,nВаВа являются корнями. Это противоречит основной теореме алгебры, которая говорит о том, что полином n-ой степени имеет ровно n корней . АВа L_n(x) имеет n+1 корней . Противоречие доказывает теорему.

Интерполяционная схема Эйткина

Поскольку при большом числе узловВа интерполяцииВа вычисление значения полинома Лагранжа по формуле (6.4) громоздко, необходимо получить рекуррентную формулу.

Пусть Вж(c)- непрерывна, узлы выбраны на отрезке [a;b] таким образом, что:

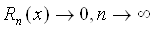
Введем функциюВаВа

x_i-узлы интерполяции;

y_i=Вж(c)

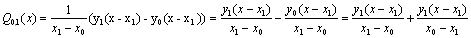
Полином Лагранжа: P_n (x) см. (6.4)

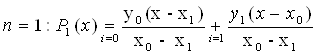
Таким образом, функция Q_0,1 (x) представляет собой полином Лагранжа l-ой степени, построенной по узлам x₀ ,x_{1ВаВаВаВаВа} Вавведем функцию вида

Функция Q_1,2 (x)- интерполяционный полином Лагранжа, построенный по узламВаВа x₁ ,x₂.

Введем теперь функциюВаВа

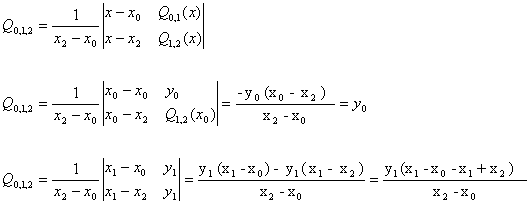
Аналогично:

Q_0,1,2 (x₂)= у_2Ва

В силу единственности полинома Лагранжа, построенного по узлам x₀, x₁ ,x_{2ВаВаВаВаВаВаВаВаВаВаВа}

функцияВа Q_0,1,2 (x) представляет собойВа интерполяционныйВа полином Лагранжа 2-ой степени, построенный по узлам x₀, x₁ ,x_2Ва .

Введем функцию:

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВа(7.1)

ВаВаВаВаВаВаВаВа Функция представляющая собой полином Лагранжа 2-ой степени, построенного по узлам x₀, x_1,тАжx_i.

Формула (7.1) позволяет рекуррентно вычислять полином Лагранжа любой степени.

Т.к. (7.1) представляет собой альтернативную форму записи интерполяционного полинома, точность приближения функции также может быть оценена по формуле (6.5)

(7.1)-интерполяционная схема Эйткина.

КОНЕЧНЫЕ РАЗНОСТИ

Пусть функция Вж(c) задана на системе равноотстоящих узлов x_i=x₀+ih,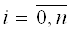

где h-шаг сетки, y_i=Вж(c_i).

Конечной разностьюВа первого порядка в точке x₀ называетсяВа ∆y₀=y₁-y₀

Конечной разностьюВа первого порядка в точке x_i: ∆y_i=y_i+1-y₀-y_i

Конечной разностьюВа второго порядка в точке x₀Ва : ∆²y₀=∆y₁-∆y₀

Конечной разностьюВа второго порядка в точке x_i: ∆²y_i=∆y_i+1-∆y_i

Общая формула для конечной разности k-того порядка в точке x_i:

∆^ky_i=∆^k-1y_i+1-∆^ky(7.2)

Заметим: ∆⁰y_i= y_i

Формула (7.2) позволяет вычислять рекуррентно конечные разности

Связь конечных разностей и производных

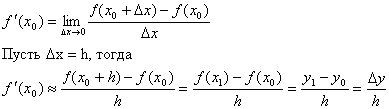
чем меньше h, тем точность выше

Аналогично можем получить связь

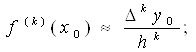
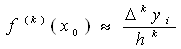;ВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВа (7.3)

Свойства конечных разностей

В связи с производными вида (7.3)конечные разности обладают свойствами:

1. постоянные, равны нулю;

2. постоянный множитель у функции выносится за знак

3. суммы 2-х функций равны сумме каждой функции

4. полинома n-ой степени, n-го порядка постоянны и равны

∆ⁿy=hⁿa_nn!

a_n-коэффициент при xⁿ полинома R_n(x)

Верно и обратное утверждение: все конечные разности n-го порядка некоторой функции постоянны и одинаковы, конечные разностиВа n +1-го порядка равны 0, а конечные разности n-1-го порядка различны, то функция представляет собой полином n-ой степени.

Распространение ошибки в исходных данныхпри вычислении конечные разности

Любые измерения несут в себе погрешность (ошибка округления, точность измерения приборов)

Пусть значения функции определены в узлах x₀,Ва 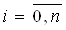ВаВаВаВаВаВаВа и в некоторой точкеВа x_kзначение некоторой точке x_kзначение функции найдено с ошибкой ε, т.еВа ỹ_k+ ε

Составим таблицу конечных разностей

x_{k-2ВаВаВаВаВаВаВаВаВаВаВаВаВа} y_k-2 ВаВаВаВаВаВаВаВаВа∆y_{k-2ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа} ∆²y_{k-2ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа} ∆³y_k-3Ва +ε

x_{k-1ВаВаВаВаВаВаВаВаВаВаВаВаВа} y_{k-1ВаВаВаВаВаВаВа} ВаВаВаВа∆y_k-1 +ε∆²y_k-2ВаВа +ε∆³y_k-2Ва -3ε

x_ky_k+εВаВаВаВаВаВаВа ∆y_k-1 -ε∆²y_k-1 -2ε∆³y_k-1Ва +3ε

x_k+1ВаВаВаВаВаВаВаВа y_{k+1Ва ВаВаВаВаВаВаВаВаВаВа} ∆y_{k+1ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа} ∆²y_k+εВаВаВаВаВаВаВаВаВаВаВаВаВаВа∆³y_k-ε

x_k+2ВаВаВаВаВаВаВаВа y_k+2 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа∆²y_k+1

Как видно из таблицы конечных разностей при увеличении порядка конечных разностей ошибка в исходных данных распространяется и растет.

Такое взаимодействие ошибок называют шумом, если это ошибки округлений - то шумом округлений.

Если ошибки округлений достаточно большие, то может происходить следующее явление: при увеличении порядкаВа конечных разностей они могут уменьшаться и→0, но, дойдя до некоторого малого значения, опять могут начать растиВа из-заВа шума округлений.

Столбец в таблице конечных разностей, в которой все конечные разности ≈0, называют Влпрактическим постояннымВ»; при этом конечные разности высших порядков не используют.

Для интерполяции целесообразно использовать многочлен такой степени, которая совпадает с порядком Влпрактической постояннойВ» конечных разностей.

ЛЕКЦИЯ №8

ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ДЛЯРАВНООТСТОЯЩИХ УЗЛОВ

Дана функция y=Вж(c),заданная на сетке равноотстоящих узлов:

y_i=Вж(c_i), x_i=x₀+ih_i,

Строим интерполяционный полином с целью упрощения записи полинома (интерполяционного) и представления его в виде,Ва позволяющем оценивать влияние каждого изВа компонентов на значение аппроксимации, запишемВа егоВа так:

N_n(x)=-a₀+a₁(x-x₀)+a₂(x-x₀)(x-x₁)+тАж+a_n(x-x₀)тАж(x-x_n-1)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.1)

Необходимо посчитать его коэффициенты a_i. Будем находить из условия

N_n(x_i)=y_i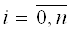

i=0: N_n(x₀)=y₀=a₀+a₁0+тАж+a_n0Ва a₀= y₀

i=1: N_n(x₁)=y₁= y₀+a₁(x₁-x₀) + a₂0+тАж+a_n0

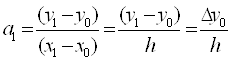
x₁=x₀+1h=x₁-x₀=h

i=2: N_n(x₂)=y₂= y₀+∆y₀/h(x₂-x₀) (x₂-x₁) + a₃0+тАж+a_n0

x₂-x₀=2h

x₂-x₁=h

y₂= y₀+∆y₀2+a₂2h²

i=k:Ва 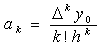ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(8.2)

Запишем теперь, используя (8.2), полином (8.1) в виде:

N_n(x)= y₀+∆y₀/h(x-x₀)+тАж+ ∆ⁿ y₀ /n!hⁿ(x-x₀)(x-x₁)тАж (x-x_n-1) (8.3)

Полином (8.3) 1-ый интерполяционный многочлен Ньютона. Он наиболееВа приспособлен для вычисления значенияВа функции в точках, близких к x₀

С целью упрощения записи полинома введем переменную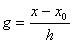

x=x₀+gh

Если g-целое, то будет совпадать с номером узла

x₀ тАУ базовый узел полинома (8.3)

x_i=x₀+gh- x₀-ih=h(g-i);

N_n(g)=Ва y₀+∆y₀g+тАж+ ∆ⁿ y₀ /n!g(g-1)(g-2)(g-n+1)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.4)

Полином Ньютона в силу единственности существования интерполяционного полинома Лагранжа является одной из форм записи полинома Лагранжа, поэтому дляВа полинома (8.3) справедливо, что формула остаточного члена полинома Лагранжа

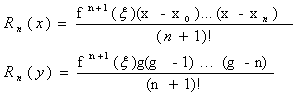
Для вычисления функции в точках находящихся в середине сетки узловВа интерполяции либо в ее конце, т. е близкие к x_n, применяют два подходаВа

1. строят формулы для вычисления функции в точках х, близких к середине сетки интерполяции

2. формулы для точек х, близких к х_n (упорядочивание узловВа интерполяции).

Соответственно получаются формулы Стирлинга , Бесселя, Гаусса, и 2-ой интерполяционный многочлен Ньютона .

Второй путь: в качестве узла х₀ для заданной точки х берут тот узел, который наиболее близок к х, узел х₁ выбирают как самый близкий из оставшихся узлов к х.

Т.е последовательностьВа 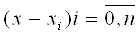упорядочившаяся по возрастанию.

Для вычисления значения функции в точке х используется 1-ый интерполяционныйВа многочлен Ньютона.

х0Ва х1ВаВаВаВаВаВа х2ВаВаВаВаВаВа х3ВаВаВаВаВаВаВаВа х4ВаВаВаВаВа х5 х6

Преобразуем узлы:

х₀′=x_3;

x₁′=x₄ ;

x₂′=x₂ ;

x₃′=x₅ ;

Разделенные разности

Пусть функцияВа Вж(c),задана на системе неравно отстоящих узлов.

Разделенной разностью 1-го порядка назовем выражение:

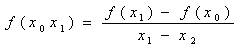
Разделенной разностью 2-го порядка:

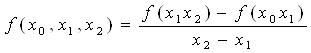
Разделенной разностью k-го порядка:

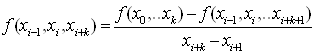(8.6)

|x-x₀|,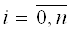

Свойства разделенной разности:

- на сетке равноотстоящих узлов разделенной разности совпадают конечными разностями

- разделенные разности понижают степень многочлена

- разделенные разности n-го порядка постоянны и равны

Интерполяционная формула Ньютона для не равноотстоящих узлов

Пусть функцияВа Вж(c), задана на сетке не равноотстоящих узлов x_i, 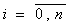.Запишем следующие разделенные разности:

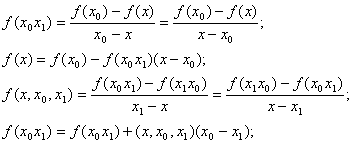
Выполним такие действия n-1 раз, получим:

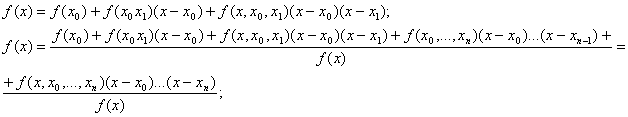Полином Ньютона:

N_n(x)=Вж⁰(c)

R_n(x)= Вж(c,c_0,тАжc_n)(x-x₀)тАж (x-x_n)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.8)

То Вж(c)= N_n(x)+ R_n(x)

N_n(x) ≈ Вж(c)

R_n(x) = Вж(c) - N_n(x)

Если Вж(c) имеет (n+1)-ую производную, тоВа остаточный член может быть преобразован к виду остаточного члена (8.9) полинома Лагранжа.

При вычисленииВа полинома в точке х узлы интерполяции лучше переименовать так, чтобы х₀ был самым близким к х, а все остальные узлы тем более удаленные по увеличению расстояния к х.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики