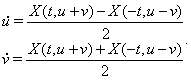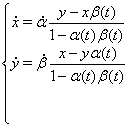Вивчення систем з постiйною парною частиною
Курсова робота
"Вивчення систем з постiйною парною частиною"
Змiст
Введення
1. Парнi й непарнi вектор-функцii
2.Основнi вiдомостi з теорii функцiй, що вiдбивають
3. Системи парна-непара
4. Побудова прикладiв систем, парна частина загального рiшення яких постiйна
5. Простi й найпростiшi системи
6. Побудова множини систем, парна частина загального рiшення яких постiйна
6.1 Системи, що мають постiйну парну частину
6.2 Побудова систем iз заданою парною частиною
Висновок
Список джерел
Введення
При вивченнi питань iснування перiодичних рiшень диференцiальних систем i рiвнянь використовуються властивостi симетричностi (парнiсть, непарнiсть i т.п.) як функцiй, що задають дослiджувану систему, так i самих рiшень.
У данiй роботi ми будемо розглядати сiмейства рiшень iз постiйною парною частиною, тобто коли парна частина буде представлена у виглядi константи.
Розберемо приклади систем, сiмейства рiшень яких мають постiйну парну частину. Будемо вивчати побудову систем iз заданою парною частиною.
1.
Парнi й непарнi вектор-функцii
За аналогiiю з функцiями одноi змiнноi, вектор-функцiю ![]() ,
, ![]() Вабудемо називати парною (непарноi), якщо для всiх
Вабудемо називати парною (непарноi), якщо для всiх ![]() ,
, ![]() Ваi парною (непарноi) функцiiю, тобто область визначення
Ваi парною (непарноi) функцiiю, тобто область визначення ![]() Васиметрична щодо нуля й
Васиметрична щодо нуля й ![]() Ва(
Ва(![]() ).
).
Будь-яку функцiю iз симетричною областю визначення, можна представити як суму парноi й непарноi функцiй. Дiйсно, якщо
![]()
![]()
![]()
i ![]() Ваi парною функцiiю, а
Ваi парною функцiiю, а ![]() ВатАУ непарноi.
ВатАУ непарноi.
![]() Вабудемо називати парною частиною функцii
Вабудемо називати парною частиною функцii ![]() ,
, ![]() ВатАУ непарноi.
ВатАУ непарноi.
Вiдзначимо наступнi властивостi парних i непарних функцiй.
Властивiсть 1 Похiдна парноi (непарноi) функцii i функцiя непарна (парна).
Доказ. a) ![]() ВатАУ парна функцiя.
ВатАУ парна функцiя.
![]()
![]()
![]()
Т.к. ![]() Ваi
Ваi ![]() Ваiснують або не iснують одночасно, те
Ваiснують або не iснують одночасно, те![]() ,
, ![]() Ваi
Ваi ![]() . Таким чином, похiдна парноi функцii i функцiя непарна.
. Таким чином, похiдна парноi функцii i функцiя непарна.
б) ![]() ВатАУ непарна функцiя.
ВатАУ непарна функцiя.
![]()
![]()
![]()
Т.к. ![]() Ваi
Ваi ![]() Ваiснують або не iснують одночасно, те
Ваiснують або не iснують одночасно, те![]() ,
, ![]() Ваi
Ваi ![]() . Таким чином, похiдна непарноi функцii i функцiя парна.
. Таким чином, похiдна непарноi функцii i функцiя парна.
Властивiсть 2
Якщо ![]() ВатАУ непарна функцiя, те
ВатАУ непарна функцiя, те ![]() .
.
Доказ. Оскiльки ![]() ВатАУ непарна функцiя, те
ВатАУ непарна функцiя, те
![]()
Пiдставивши замiсть ![]()
![]() Ваодержуiмо
Ваодержуiмо ![]()
Звiдки треба ![]()
2.
Основнi вiдомостi з теорii функцiй, що вiдбивають
Розглянемо систему
уважаючи, що ii права частина безперервна й маi безперервнi частки похiднi по ![]() . Загальне рiшення цiii системи у формi Кошi позначимо через
. Загальне рiшення цiii системи у формi Кошi позначимо через ![]() . Через
. Через ![]() Вапозначимо iнтервал iснування рiшення
Вапозначимо iнтервал iснування рiшення ![]()
Нехай
![]()
Визначення: функцiiю, що вiдбиваi, (1) системи назвемо функцiю
![]()
обумовлену формулою
або формулами
![]()
Для функцii, що вiдбиваi, справедливi властивостi:
1) Для будь-якого рiшення
![]()
системи (1) вiрна тотожнiсть
2) Для функцii, що ![]() Вавiдображаi, будь-якоi системи виконанi тотожностi:
Вавiдображаi, будь-якоi системи виконанi тотожностi:
3) Диференцюiма функцiя
![]()
буде функцiiю, що вiдбиваi, (1) системи тодi й тiльки тодi, коли вона задовольняi рiвнянням у частинних похiдних
i початковiй умовi
Рiвняння (5) будемо називати основним рiвнянням (основним спiввiдношенням) для функцii, що вiдбиваi.
Доказ. Властивiсть 1) треба безпосередньо з визначення (2). Для доказу властивостi 2) помiтимо, що вiдповiдно до властивостi 1) для будь-якого рiшення ![]() Васистеми (1) вiрнi тотожностi
Васистеми (1) вiрнi тотожностi
![]()
РЖз цих тотожностей у силу того, що через кожну крапку ![]() Вапроходить деяке рiшення
Вапроходить деяке рiшення ![]() Васистеми (1), i випливають тотожностi (5).
Васистеми (1), i випливають тотожностi (5).
Приступимося до доказу властивостi 3). Нехай ![]() ВатАУ функцiя, що вiдбиваi, (1)системи . Тодi для неi вiрна тотожнiсть (3). Диференцiюiмо цю тотожнiсть по
ВатАУ функцiя, що вiдбиваi, (1)системи . Тодi для неi вiрна тотожнiсть (3). Диференцiюiмо цю тотожнiсть по ![]() Вай скористаiмося тим, що
Вай скористаiмося тим, що ![]() ВатАУ рiшення системи (1), i самою тотожнiстю (3). Одержимо тотожнiсть
ВатАУ рiшення системи (1), i самою тотожнiстю (3). Одержимо тотожнiсть
![]()
з якого в силу довiльностi рiшення ![]() Ватреба, що
Ватреба, що ![]() ВатАУ рiшення системи (5). Початкова умова вiдповiдно до властивостi 2) так само виконуiться.
ВатАУ рiшення системи (5). Початкова умова вiдповiдно до властивостi 2) так само виконуiться.
Нехай деяка функцiя ![]() Вазадовольняi системi (5) й умовi (6). Тому що цiй системi й цiй умовi задовольняi так само й функцiя, що вiдбиваi, то з одиничностi рiшення (5) задачi (6) -
Вазадовольняi системi (5) й умовi (6). Тому що цiй системi й цiй умовi задовольняi так само й функцiя, що вiдбиваi, то з одиничностi рiшення (5) задачi (6) - ![]() Вафункцiя повинна збiгатися з функцiiю, що вiдбиваi. Властивiсть 3) доведено.
Вафункцiя повинна збiгатися з функцiiю, що вiдбиваi. Властивiсть 3) доведено.
Лема Основна лема 3 Нехай права частина системи (1) ![]() -перiодична по
-перiодична по ![]() , безперервна й маi безперервнi частки похiднi по змiнним
, безперервна й маi безперервнi частки похiднi по змiнним ![]() . Тодi вiдображення за перiод для системи (1) можна знайти по формулi
. Тодi вiдображення за перiод для системи (1) можна знайти по формулi
![]()
i тому рiшення ![]()
системи (1) буде ![]() - перiодичним тодi й тiльки тодi, коли
- перiодичним тодi й тiльки тодi, коли ![]() Ваi рiшення недиференцiальноi системи
Ваi рiшення недиференцiальноi системи
Як наслiдок цiii леми доведемо наступне припущення.
Твердження 4
Нехай безупинно диференцюiма функцiя ![]()
![]() -перiодична й нечетна по
-перiодична й нечетна по ![]() , тобто
, тобто
![]()
и. ![]() ВаТодi всяке продовження на вiдрiзок
ВаТодi всяке продовження на вiдрiзок ![]() Варiшення системи (1) буде
Варiшення системи (1) буде ![]() -перiодичним i парним по
-перiодичним i парним по ![]() .
.
Доказ. Для доказу досить помiтити, що функцiя ![]() Вазадовольняi рiвнянню (5) й умовi (6). Тому вона вiдповiдно до властивостi 3) i функцiiю, що вiдбиваi, розглянутоi системи. Рiвняння (7) в нашiм випадку вироджуiться в тотожнiсть, i йому задовольняi кожне
Вазадовольняi рiвнянню (5) й умовi (6). Тому вона вiдповiдно до властивостi 3) i функцiiю, що вiдбиваi, розглянутоi системи. Рiвняння (7) в нашiм випадку вироджуiться в тотожнiсть, i йому задовольняi кожне ![]() , для якого визначене значення
, для якого визначене значення
![]()
Вiдповiдно до основноi леми будь-яке рiшення системи (1) буде ![]() -перiодичним. Парнiсть довiльного рiшення
-перiодичним. Парнiсть довiльного рiшення ![]() Васистеми (1) треба з тотожностей
Васистеми (1) треба з тотожностей
![]()
справедливих у силу властивостi 1) функцii, що вiдбиваi.
Справедливi наступнi твердження [4].
Теорема 5 Нехай всi рiшення системи (1) ![]() -перiодичнi й однозначно визначаються своiми початковими даними. Тодi, що вiдбиваi функцiя,
-перiодичнi й однозначно визначаються своiми початковими даними. Тодi, що вiдбиваi функцiя, ![]() Вацiii системи
Вацiii системи ![]() -перiодична по
-перiодична по ![]()
Теорема 6 Нехай система (1) ![]() -перiодична по
-перiодична по ![]() Ваа ii рiшення однозначно визначаються своiми початковими даними й iснують при всiх
Ваа ii рiшення однозначно визначаються своiми початковими даними й iснують при всiх ![]() ВаЯкщо, крiм того, що вiдбиваi функцiя цiii системи
ВаЯкщо, крiм того, що вiдбиваi функцiя цiii системи ![]() -перiодична по
-перiодична по ![]() Вате всi рiшення системи (1) перiодичнi з перiодом
Вате всi рiшення системи (1) перiодичнi з перiодом ![]()
Аналогiчна теорема маi мiсце в тому випадку, коли не всi рiшення системи (1) продовжимi на вiдрiзок ![]() ВаПри цьому висновок про
ВаПри цьому висновок про ![]() -перiодичнiсть можна зробити лише для тих рiшень, якi iснують при всiх
-перiодичнiсть можна зробити лише для тих рiшень, якi iснують при всiх ![]()
З ![]() -перiодичностi функцii, що вiдбиваi,
-перiодичностi функцii, що вiдбиваi, ![]() треба -перiодичнiсть всiх продовжимих
треба -перiодичнiсть всiх продовжимих ![]() Вана рiшення перiодичноi (1)системи . З
Вана рiшення перiодичноi (1)системи . З ![]() -перiодичностi функцii, що вiдбиваi, не треба, загалом кажучи
-перiодичностi функцii, що вiдбиваi, не треба, загалом кажучи![]() , -перiодичнiсть
, -перiодичнiсть ![]() рiшень -перiодичноi системи, хоча треба
рiшень -перiодичноi системи, хоча треба ![]() iх -перiодичнiсть.
iх -перiодичнiсть.
Не слiд думати, що якщо всi рiшення ![]() -перiодичноi системи
-перiодичноi системи ![]() -перiодичнi, те ii функцiя, що вiдбиваi, зобов'язана
-перiодичнi, те ii функцiя, що вiдбиваi, зобов'язана ![]() бути -перiодичноi. Цьому суперечить приклад рiвняння
бути -перiодичноi. Цьому суперечить приклад рiвняння ![]()
У випадку, коли ![]() , тобто коли система (1) вироджуiться в рiвняння, вiрна
, тобто коли система (1) вироджуiться в рiвняння, вiрна
Теорема 7 Нехай рiвняння (1) ![]() -перiодичне по
-перiодичне по ![]() Ваа його рiшення однозначно визначаються своiми початковими даними й iснують при всiх
Ваа його рiшення однозначно визначаються своiми початковими даними й iснують при всiх ![]() ВаТодi для того, щоб всi рiшення рiвняння (1) були
ВаТодi для того, щоб всi рiшення рiвняння (1) були ![]() -перiодичнi, необхiдна й достатня
-перiодичнi, необхiдна й достатня ![]() -перiодичнiсть по
-перiодичнiсть по ![]() Вафункцii, що вiдбиваi, цього рiвняння.
Вафункцii, що вiдбиваi, цього рiвняння.
3.
Системи парна-непара
Розглянемо систему
Будемо вважати, що всюди надалi ця система задовольняi умовам:
а) Функцiя ![]() Вабезупинно диференцюiма, i тому, задача Кошi для системи (8) маi iдине рiшення;
Вабезупинно диференцюiма, i тому, задача Кошi для системи (8) маi iдине рiшення;
б) Права частина системи (8) ![]() -перiодична по
-перiодична по ![]() .
.
Лема 8
Нехай система (8) задовольняi умовам а) i б). Тодi продовжинi на вiдрiзок ![]() Варiшення
Варiшення ![]() Вацiii системи буде
Вацiii системи буде ![]() -перiодичним тодi й тiльки тодi, коли
-перiодичним тодi й тiльки тодi, коли
![]()
![]()
тАУ i непарна частина рiшення ![]() .
.
Доказ. Нехай ![]() ВатАУ
ВатАУ ![]() -перiодичне рiшення системи (8). Тодi
-перiодичне рiшення системи (8). Тодi
![]()
Необхiднiсть доведена.
Нехай ![]() ВатАУ рiшення системи (8), для якого
ВатАУ рiшення системи (8), для якого ![]() . Тодi
. Тодi
![]()
i тому
![]()
Таким чином, крапка ![]() Ваi нерухлива крапка вiдображення за перiод, а рiшення
Ваi нерухлива крапка вiдображення за перiод, а рiшення ![]() ВатАУ
ВатАУ ![]() -перiодичне.
-перiодичне.
Доведена лема, питання про перiодичнiсть рiшення
![]()
зводить до обчислення одного зi значень непарноi частини ![]() . РЖнодi вiдносно
. РЖнодi вiдносно ![]() Ваможна сказати бiльше, нiж про саме рiшення
Ваможна сказати бiльше, нiж про саме рiшення ![]() . Це дозволяi в таких випадках робити рiзнi висновки щодо iснування перiодичних рiшень у систем виду (8). Диференцуiмi функцii
. Це дозволяi в таких випадках робити рiзнi висновки щодо iснування перiодичних рiшень у систем виду (8). Диференцуiмi функцii
![]()
![]()
задовольняють деякiй системi диференцiальних рiвнянь. Перш, нiж виписати цю систему, помiтимо:
тому що
![]()
рiшення системи (8). Замiняючи в тотожностi (9) ![]() Вана
Вана ![]() Вай з огляду на, що похiдна парноi функцii тАУ функцiя непарна, а похiдна непарноi функцii тАУ функцiя парна, одержуiмо тотожнiсть
Вай з огляду на, що похiдна парноi функцii тАУ функцiя непарна, а похiдна непарноi функцii тАУ функцiя парна, одержуiмо тотожнiсть
З тотожностей (9) i (10) знайдемо похiднi:
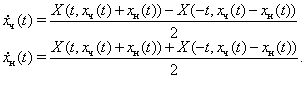
У такий спосiб вектор-функцiя
задовольняi наступнiй системi диференцiальних рiвнянь порядку ![]() :
:
![]()
Систему (12) будемо називати системою пар-непара, що вiдповiдаi системi (8). рiшення системи чiт-непара, як треба з умови а), однозначно визначаiться своiми початковими умовами.
4.
Побудова прикладiв систем, парна частина загального рiшення яких постiйна
Приклад
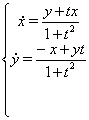
Знайдемо рiшення: будемо використовувати метод виключення, вiзьмемо перше рiвняння системи й виразимо з нього ![]() :
:
![]()
тепер диференцiюiмо його
![]()
Ми можемо дорiвняти лiву частину отриманого рiвняння з лiвою частиною другого рiвняння вихiдноi системи
![]()
Зробимо перетворення й приведемо подiбнi
![]()
![]()
![]()
![]()
![]()
![]()
![]()
У такий спосiб:
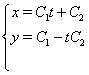
Зробимо перевiрку, для цього у вихiдну систему пiдставимо отримане рiшення:
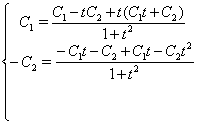
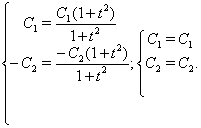
Одержали вiрнi рiвностi. Значить було знайдено правильне рiшення вихiдноi системи.
Парна частина загального рiшення:
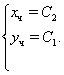
Приклад
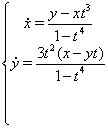
Знайдемо рiшення: будемо використовувати метод виключення, вiзьмемо перше рiвняння системи й виразимо з нього ![]() :
:
![]()
тепер диференцiюiмо його
![]()
Ми можемо дорiвняти лiву частину отриманого рiвняння з лiвою частиною другого рiвняння вихiдноi системи
![]()
Зробимо перетворення й приведемо подiбнi
![]()
![]()
![]()
![]()
![]()
![]()
У такий спосiб:
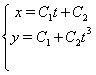
Зробимо перевiрку:
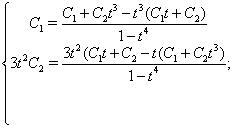
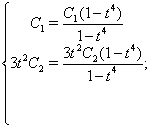
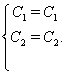
Парна частина загального рiшення
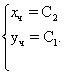
Приклад
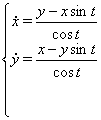
Знайдемо рiшення: будемо використовувати метод виключення, вiзьмемо перше рiвняння системи й виразимо з нього ![]() :
:
![]()
тепер диференцiюiмо його
![]()
Ми можемо дорiвняти лiву частину отриманого рiвняння з лiвою частиною другого рiвняння вихiдноi системи
![]()
![]()
![]()
![]()
Одержали два рiшення ![]() Вай
Вай ![]() .
.
1) ![]() ;
;
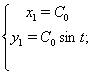
2) ![]() ;
;
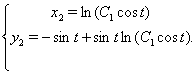
Зробимо перевiрку для ![]() :
:
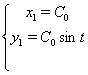
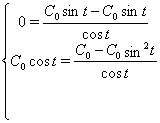
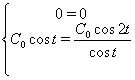
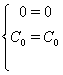
Одержали вiрнi рiвностi. Значить було знайдено правильне рiшення вихiдноi системи.
Зробимо перевiрку для ![]() :
:
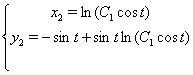
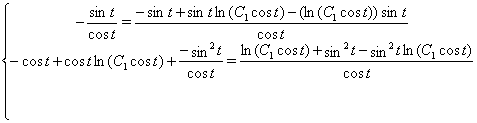
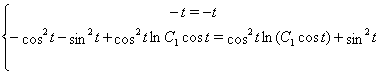
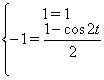
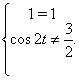
Звiдси видно, що ![]() Ване i рiшенням для вихiдноi системи.
Ване i рiшенням для вихiдноi системи.
У такий спосiб:
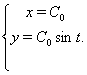
Парна частина загального рiшення
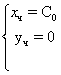
З даних прикладiв можемо помiтити, що рiшення систем записуiться у виглядi:
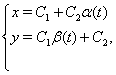
де ![]() Вай
Вай ![]() ВатАУ непарнi функцii, а парна частина представлена константою.
ВатАУ непарнi функцii, а парна частина представлена константою.
![]()
![]() ;
;
![]() ;
;
Системи виду (13) будуть мати сiмейства рiшень iз постiйною парною частиною. У цьому легко переконаiться, проробивши обчислення, аналогiчнi попереднiм прикладам.
5.
Простi й найпростiшi системи
Лема 9
Для всякоi безупинно диференцюiмоi функцii
![]()
для якоi виконанi тотожностi (4), мають мiсце спiввiдношення
![]()
![]()
Теорема 10
Для всякоi двiчi безупинно диференцюiмоi функцii ![]() Вапевноi в симетричнiй областi
Вапевноi в симетричнiй областi ![]() , що мiстить гiперплощина
, що мiстить гiперплощина ![]() Вадля якоi виконанi тотожностi (4), iснуi диференцiальна система
Вадля якоi виконанi тотожностi (4), iснуi диференцiальна система ![]() Ваc безупинно диференцюiмоi правою частиною, що вiдбиваi функцiя якоi збiгаiться с.
Ваc безупинно диференцюiмоi правою частиною, що вiдбиваi функцiя якоi збiгаiться с.![]()
Теорема 11
Для всякоi двiчi безупинно диференцюiмоi функцii
![]()
певноi в областi ![]() Ваутримуюча гiперплощина
Ваутримуюча гiперплощина ![]() , для якоi виконанi тотожностi (4), при всiх
, для якоi виконанi тотожностi (4), при всiх ![]() Ваi досить малих
Ваi досить малих ![]() Ваiснуi диференцiальна система
Ваiснуi диференцiальна система
![]()
функцiя, що вiдбиваi, якоi збiгаiться ![]() Ваз а загальний iнтеграл задаiться формулою
Ваз а загальний iнтеграл задаiться формулою
![]()
Наслiдок 12 Двiчi безупинно диференцюiма функцiя
![]()
i функцiiю, що вiдбиваi, хоча б однiii диференцiальноi системи тодi й тiльки тодi, коли для неi виконанi (4)тотожностi .
Системи, iснування яких гарантуiться теоремами 10 й 11, називаються вiдповiдно простiй i найпростiшоi.
Теорема 13 Нехай
![]()
найпростiша система, тодi
![]()
де ![]() ВатАУ функцiя, що вiдбиваi, (1)системи .
ВатАУ функцiя, що вiдбиваi, (1)системи .
Доказ. Якщо система найпростiша,
![]()
![]()
Теорема 14 Нехай
![]()
i функцiя, що вiдбиваi, деякоi диференцiальноi системи, рiшення якоi однозначно визначаються своiми початковими даними, а для безупинно диференцюiмоi функцii
![]()
виконано тотожностi (4). Тодi для того, щоб в областi ![]() Вафункцiя
Вафункцiя ![]() Вазбiгалася з
Вазбiгалася з ![]() Ванеобхiдно й досить, щоб розглянута система мала вигляд
Ванеобхiдно й досить, щоб розглянута система мала вигляд
![]()
або вид
![]()
Де ![]()
i деяка безперервна вектор-функцiя.
Будемо говорити, що множина систем виду (1) утворить клас еквiвалентностi, якщо iснуi диференцюiма функцiя
![]()
iз властивостями:
1) функцiя, яка вiдбиваi
![]()
будь-якоi системи з розглянутоi множини збiгаiться у своiй областi визначення ![]() Ваз функцiiю
Ваз функцiiю ![]()
2) Будь-яка система виду (1), що вiдбиваi функцiя
![]()
яке збiгаiться в областi ![]() Ваз функцiiю
Ваз функцiiю ![]() Вавтримуiться в розглянутiй множинi.
Вавтримуiться в розглянутiй множинi.
Двi системи виду (1), що належать одному класу еквiвалентностi, будемо називати еквiвалентними. Допускаючи певну вiльнiсть мови, будемо говорити також, що вони мають ту саму функцiю, що вiдбиваi. Функцiю ![]() Вапри цьому будемо називати функцiiю, що вiдбиваi, класу, а клас - вiдповiдноi функцii, що
Вапри цьому будемо називати функцiiю, що вiдбиваi, класу, а клас - вiдповiдноi функцii, що ![]() вiдбиваi .
вiдбиваi .
РЖз третьоi властивостi функцii, що вiдбиваi, треба, що (1) система й система
![]()
належать одному класу еквiвалентностi тодi й тiльки тодi, коли система рiвнянь
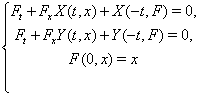
Сумiсна
Необхiдною умовою спiльностi цiii системи i тотожнiсть ![]() .
.
6.
Побудова множини систем, парна частина загального рiшення яких постiйна
6.1
Системи, що мають постiйну парну частину
Нехай нам дана система
Перед нами встаi наступне питання про те, коли сiмейство рiшень цiii системи будуть мати постiйну парну частину.
Тобто, коли ![]() Ване буде залежати вiд часу
Ване буде залежати вiд часу ![]() .
.
Вiзьмемо функцiю, що вiдбиваi, (14) ![]() Васистеми й використовуючи
Васистеми й використовуючи
![]()
одержимо парну частину в такий спосiб:
Теорема 15 Якщо виконано тотожнiсть
![]()
де ![]() ВатАУ функцiя, що вiдбиваi, для лiнiйноi системи (14)виду , те будь-яке рiшення цiii системи маi постiйну парну частину.
ВатАУ функцiя, що вiдбиваi, для лiнiйноi системи (14)виду , те будь-яке рiшення цiii системи маi постiйну парну частину.
Доказ. Вiзьмемо будь-яке рiшення ![]() Васистеми (14). Його похiдна
Васистеми (14). Його похiдна
![]()
Тому можемо записати
![]()
З умови теореми маiмо
![]()
У такий спосiб одержали, що ![]() ВатАУ парна вектор-функцiя. Тодi
ВатАУ парна вектор-функцiя. Тодi
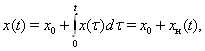
6.2
Побудова систем iз заданою парною частиною
Розглянемо систему (14). Будемо будувати систему iз заданою парною частиною.
Нехай нам вiдома парна частина ![]() . Скористаiмося формулою (15) й перетворимо ii
. Скористаiмося формулою (15) й перетворимо ii
![]()
Отже, можемо записати
![]()
Звiдси знаючи (3), одержимо
![]()
де ![]() ВатАУ функцiя, що вiдбиваi, системи. Крiм
ВатАУ функцiя, що вiдбиваi, системи. Крiм ![]() Ваiз попереднього спiввiдношення, з довiльною функцiiю, що
Ваiз попереднього спiввiдношення, з довiльною функцiiю, що ![]() вiдбиваi , задовольняючiй умовi
вiдбиваi , задовольняючiй умовi
![]()
одержимо необхiдну систему.
Приклад 16
Нехай
![]()
де ![]() ВатАУ задана парна частина,
ВатАУ задана парна частина, ![]() . Диференцiюiмо обидвi частини рiвностi
. Диференцiюiмо обидвi частини рiвностi
![]()
Перетворимо праву частину
![]()
Перепишемо отримане у виглядi:
![]()
Виразимо ![]() :
:
Для всiх систем виду (17) повинне бути виконане умова
![]()
Вiзьмемо
![]()
Знайдемо ![]() ,
, ![]() .
. ![]() ;
;
![]()
Пiдставимо значення ![]() ,
, ![]() Вау систему (17):
Вау систему (17):
![]()
![]()
![]()
Одержуiмо необхiдну систему:
![]()
Приклад 17
Нехай
![]()
де ![]() ВатАУ задана парна частина,
ВатАУ задана парна частина, ![]() . Диференцiюiмо обидвi частини рiвностi
. Диференцiюiмо обидвi частини рiвностi
![]()
i перетворимо праву частину
![]()
Перепишемо отримане у виглядi:
![]()
Виразимо ![]() :
:
Для всiх таких систем повинне бути виконане умова ![]() .
.
Вiзьмемо ![]() . Знайдемо
. Знайдемо ![]() ,
, ![]() .
. ![]() ,
,
![]()
Пiдставимо знайденi значення в систему (18) й зробивши перетворення аналогiчнi прикладу 16, одержуiмо:
![]()
Розглянемо тепер загальний випадок, коли нам задана парна частина ![]() Вазагального рiшення системи з функцiiю, що
Вазагального рiшення системи з функцiiю, що ![]() вiдбиваi . У цьому випадку
вiдбиваi . У цьому випадку
![]()
Тому, якщо ![]() Ванам задана, то зi спiввiдношення
Ванам задана, то зi спiввiдношення
![]()
при заданiй ![]() Вами знайдемо загальне рiшення
Вами знайдемо загальне рiшення ![]() Вашуканоi системи. Саму систему ми побудуiмо крiм
Вашуканоi системи. Саму систему ми побудуiмо крiм ![]() Вазi спiввiдношень
Вазi спiввiдношень
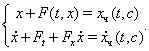
Таким чином, ми прийшли до
Теорема 18
Усяка система
де ![]() Ваперебувають iз системи
Ваперебувають iз системи
![]()
при будь-якоi заданоi диференцiюiмоi функцii ![]() , що задовольняi спiввiдношенням
, що задовольняi спiввiдношенням
![]()
маi загальне рiшення з парною частиною ![]() .
.
Якщо
![]()
те система (19) маi вигляд:
![]()
Таким чином, ми прийшли до висновку:
Наслiдок 19
Загальне рiшення диференцiальноi системи маi постiйну парну частину тодi й тiльки тодi, коли ця система найпростiша.
Висновок
Основним результатом даноi роботи i побудова диференцiальних систем, сiмейство рiшень яких маi задану парну частину. А так само теорема про зв'язок найпростiшоi системи й системи, сiмейство рiшень якоi маi постiйну парну частину.
Теорема. Загальне рiшення диференцiальноi системи маi постiйну парну частину тодi й тiльки тодi, коли ця система найпростiша.
Список джерел
[1]
Арнольд В.РЖ., Звичайнi диференцiальнi рiвняння. тАУ К., 2004
[2]
Бiбiков Ю.Н., Загальний курс диференцiальних рiвнянь. тАУ К., 1999
[3]
Еругин Н.П., Книга для читання за загальним курсом диференцiальних рiвнянь.3-е видання. тАУ К., 2000
[4]
Мироненко В.И., Функцiя й перiодичнi рiшення диференцiальних рiвнянь. тАУ К., 2004
[5]
Понтрягин Л.С., Звичайнi диференцiальнi рiвняння. тАУ К., 2003
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики