Рiвномiрне наближення функцiй ермiтовими сплайнами
Мiнiстерство освiти i науки Украiни
Нацiональний унiверситет "Львiвська полiтехнiка"
Курсова робота
на тему:
"Рiвномiрне наближення функцiй ермiтовими сплайнами"
Львiв 2009р
Змiст
Вступ
1. Означення ермiтових сплайнiв з експоненцiальними ланками
2. Знаходження аналiтичних виразiв для параметрiв сплайна з експоненцiальною ланкою
3. Многочленнi ермiтовi сплайни
4. Похибки наближення ермiтовими сплайнами
5. Рiвномiрне наближення ермiтовими сплайнами
Висновок
Список використаноi лiтератури
Додаток
Вступ
Наближення функцiй необхiдне для практичних розрахункiв пiд час проведення наукових дослiджень i в багатьох областях технiки. Аналiтично заданi функцii, якi представленi складним виразом, часто необхiдно замiнити простiшим виразом, так, щоб зберiгались iх властивостi. Це потрiбно для обчислення функцiй на ЕОМ.
Методи iнтерполювання многочленом Лагранжа або Ньютона на вiдрiзку 
Вапри використаннi великоi кiлькостi вузлiв iнтерполяцii часто призводять до поганого наближення, що пояснюiться значним накопиченням похибки пiд час обчислень. Крiм того, через розбiжнiсть процесу iнтерполяцii збiльшення кiлькостi вузлiв не обовтАЩязково приводить до пiдвищення точностi.
Ще одним iз способiв iнтерполювання на вiдрiзку i iнтерполювання з використанням сплайн функцiй. Сплайн функцiiю або сплайном називають кусково-полiномiальну функцiю, що визначена на вiдрiзку Варазом з певним числом неперервних похiдних.
Перевага сплайнiв над звичайною iнтерполяцiю i, по-перше, iх збiжнiсть i, по-друге, стiйкiсть процесу обчислення.
Ряд задач вимагаi наближення не тiльки самоi функцii, а й ii похiдних. Для цього використовують ермiтовi сплайни. З метою покращення точностi наближення функцiй сплайнами як ланки можна використовувати не тiльки многочлени, а й нелiнiйнi за параметрами вирази.
1. Означення ермiтових сплайнiв з нелiнiйним за параметрами виразами в ланках
Наведемо означення ермiтових сплайнiв з нелiнiйними за параметрами виразами в ланках (далi нелiнiйнi ермiтовi сплайни) з парною i непарною кiлькiстю параметрiв.
На множинi 
Вазаданi значення функцii 
Вата ii похiдних до 
- го порядку включно. Потрiбно побудувати ермiтовий сплайн (тобто вирази для параметрiв ланки) з експоненцiальною ланкою:
Ва(1)
де 
Ва- параметри ланки сплайна; 
Ва- кiлькiсть параметрiв 
.
Означення 1. Нехай 
. На множинi Вазаданi значення функцii 
Вата ii похiдних до - го порядку включно. Нелiнiйним ермiтовим сплайном з парною кiлькiстю параметрiв 
Ваназиватимемо функцiю
Ва, (2)
яка задовольняi систему рiвнянь
Ва, (3)
де 
- параметри сплайна на 
-й ланцi; 
- функцiя Хевiсайда:
РЖз системи (3) випливаi, що 
. Вираз 
Ваназиваiться ланкою ермiтового сплайна. Похибка наближення функцii Ваза допомогою ермiтового сплайна 
Вахарактеризуiться зваженою вiддаллю (функцiiю похибки)
. (4)
Означення 2. Нехай . На множинi Вазаданi значення функцii Вата ii похiдних до - го порядку включно, а на множинi 
Вазаданi значення функцii . Нелiнiйним ермiтовим сплайном з непарною кiлькiстю параметрiв 
Ваназиватимемо функцiю виду (2), яка задовольняi систему рiвнянь:
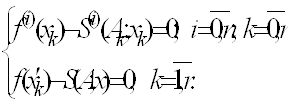Ва(5)
РЖз означень випливаi, що для визначення параметрiв кожноi ланки конкретного нелiнiйного ермiтового сплайна необхiдно розвтАЩязати систему рiвнянь (3) або (5).
2. Вивiд формул для параметрiв ермiтових сплайнiв з експоненцiальними ланками
Сiмейство цих ермiтових сплайнiв маi ланку, яку подано виразом (1). Оскiльки наближаючий вираз (1) не змiнюi знака, то цим виразом можна наближати функцii, що не змiнюють знака. Припустимо для конкретностi, що 
. Побудуiмо ланки ермiтового сплайна при 
.
При 
Ваотримаiмо ермiтовий сплайн з парною кiлькiстю параметрiв 
.
Ланка такого сплайна маi вигляд
. (6)
Згiдно означення 1 параметри ланки ермiтового сплайна (2) з ланкою (6) задовольняють системi рiвнянь (3)
Ва(7)
де 
- лiва, а 
- права границi ланки; 
,
.
ВаРозвтАЩяжемо систему (7) щодо невiдомих 
.
РЖз першого i третього рiвнянь системи знаходимо вирази для параметра 
:
Ва(8)
Прирiвнюiмо мiж собою вирази для Ваi отримаiмо вираз для 
:
Ва(9)
Пiдставляiмо перший вираз для Ваi вираз для в друге рiвняння системи (7) i отримаiмо
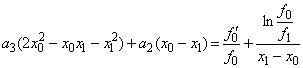Ва(10)
Пiдставляiмо другий вираз для Ваi вираз для в четверте рiвняння системи (7) i отримаiмо
Ва(11)
Ми отримали систему двох лiнiйних рiвнянь (10) i (11) щодо двох невiдомих 
. РозвтАЩязавши ii, отримаiмо
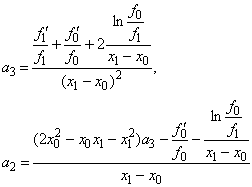Ва(12)
РЖз формул (8), (9), (10) для параметрiв 
випливаi, що необхiдною умовою iснування наближення ермiтовим сплайном з ланкою (7) i виконання умови.
При 
отримаiмо ермiтовий сплайн з непарною кiлькiстю параметрiв 
. Ланка такого сплайна маi вигляд
Ва(13)
Згiдно з означенням 2 параметри ланки (13) ермiтового сплайна (2) задовольняють системi рiвнянь (5):
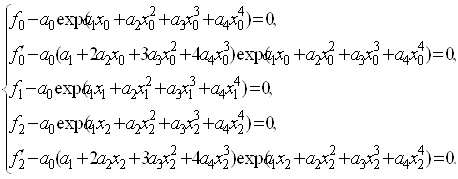Ва(14)
де 
. РозвтАЩяжемо систему (14) щодо невiдомих 
. РЖз першого, третього i четвертого рiвнянь системи (14) знайдемо вирази для
. (15)
Прирiвняiмо вирази для (15) iз першого i четвертого та першого i третього рiвнянь системи (14), отримаiмо два вирази для
Ва, (16)
Ва. (17)
Прирiвнявши мiж собою вирази для Ваiз (16) i (17), отримаiмо рiвняння
Ва(18)
Де
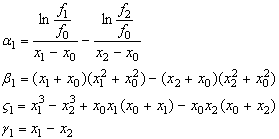
Пiдставивши перший вираз для (15) i перший вираз для (16) в друге рiвняння системи (14) отримаiмо рiвняння
Ва(19)
Де
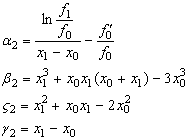
Пiдставивши третiй вираз для (15) i перший вираз для (16) в птАЩяте рiвняння системи (14) отримаiмо рiвняння
Ва(20)
де
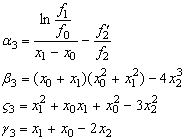
Ми отримали систему трьох лiнiйних рiвнянь (18-20) щодо трьох невiдомих 
. РозвтАЩязавши ii отримаiмо
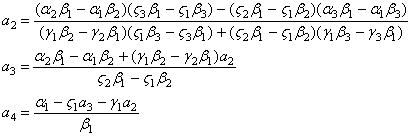Ва(21)
РЖз формул (15), (16), (17) i (21) для параметрiв 
Вавипливаi, що необхiдною умовою iснування наближення ермiтовим сплайном з ланкою (13) i виконання умови .
3. Многочленнi ермiтовi сплайни
При Ваотримаiмо ермiтовий сплайн з парною кiлькiстю параметрiв .
Ланка такого сплайна маi вигляд
Ва. (22)
Означення 3. Нехай 
, 
Ва- многочлен 3-го степеня На множинi Вазаданi значення функцii Вата ii похiдноi. Кубiчним ермiтовим сплайном називатимемо функцiю з ланкою (22)
Ва, (23)
яка задовольняi систему рiвнянь
Ва(24)
де 
- параметри сплайна на -й ланцi;
Згiдно означення 3 параметри ланки ермiтового сплайна (23) з ланкою (22) задовольняють системi рiвнянь (24)
Ва(25)
де - лiва, а - права границi ланки; ,. РозвтАЩяжемо систему (25) щодо невiдомих 
. Отримаiмо формули для обчислень значень параметрiв:
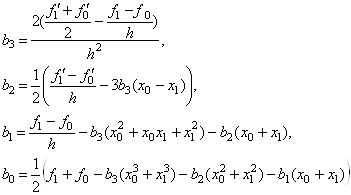Ва(26)
При отримаiмо ермiтовий сплайн з непарною кiлькiстю параметрiв . Ланка такого сплайна маi вигляд
Ва(27)
Означення 4. Нехай , 
Ва- многочлен 4-го степеня. На множинi Вазаданi значення функцii Вата ii похiдних до - го порядку включно, а на множинi Вазаданi значення функцii . Многочленним ермiтовим сплайном 4-го степеня називатимемо функцiю виду (3), яка задовольняi систему рiвнянь
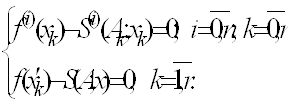Ва(28)
Згiдно з означенням 4 параметри ланки (27) ермiтового сплайна (23) задовольняють системi рiвнянь (28):
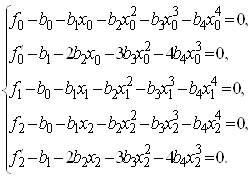Ва(29)
де . РозвтАЩяжемо систему (29) щодо невiдомих 
. РЖз першого, третього i четвертого рiвнянь системи (29) знайдемо вирази для 
. (30)
Прирiвняiмо вирази для (31) iз першого i четвертого та першого i третього рiвнянь системи (29), отримаiмо два вирази для 
Ва(31)
Ва(32)
Прирiвнявши мiж собою вирази для Ваiз (32) i (33), отримаiмо рiвняння
Ва(33)
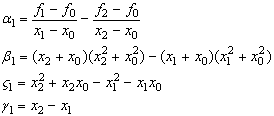
Пiдставивши перший вираз для (30) i перший вираз для (31) в друге рiвняння системи (29) отримаiмо рiвняння
Ва(34)
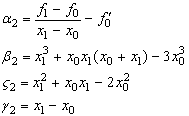
Пiдставивши третiй вираз для (30) i перший вираз для (31) в птАЩяте рiвняння системи (30) отримаiмо рiвняння
Ва(35)
Ми отримали систему трьох лiнiйних рiвнянь (23-35) щодо трьох невiдомих 
. РозвтАЩязавши ii отримаiмо
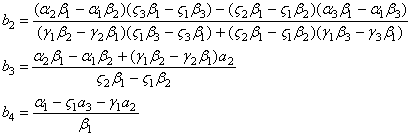Ва(36)
РЖз формул (30), (31), (32) i (36) для параметрiв 
Вавипливаi, що необхiдною умовою iснування наближення ермiтовим сплайном з ланкою (27) i виконання умови .
4. Похибки наближення ермiтовими сплайнами
Максимальна похибка 
Варiвномiрного наближення нелiнiйними ермiтовими сплайнами з парною кiлькiстю параметрiв у ланцi маi вигляд
, (37)
а для ермiтових сплайнiв з непарною кiлькiстю параметрiв
Ва(38)
де 
Ва- кiлькiсть ланок сплайна на iнтервалi , 
- вагова функцiя, 
Ва- ядро похибки наближення, 
Ва- дефект ермiтового сплайна, 
. Для ермiтового сплайна з ланкою (13) кiлькiсть параметрiв , дефект сплайна за означенням 
, величина 
. Щоб скористатись формулами (37) i(38), потрiбно мати вираз для ядра похибки наближення 
, який би не залежав вiд параметрiв 
ланки сплайна 
. Вирази для конкретних ядер можна знайти, використовуючи властивостi ядер похибок, якi випливають iз обмiнних теорем.
Теорема 1. Нехай для функцii 
Вапри 
Ваiснуi iдине наближення ермiтовим сплайном з парною кiлькiстю параметрiв з вузлами 
Ваi ланками вигляду
Ва(39)
Тодi для функцii 
Вана промiжку 
Ваз тими ж вузлами iснуi iдине наближення ермiтовим сплайном з парною кiлькiстю параметрiв i ланками вигляду
Ва(40)
Нехай 
ВатАФ найбiльша вiдносна похибка наближення функцii 
Вана промiжку
Ваермiтовим сплайном з ланкою (39), а 
ВатАФ найбiльша вiдносна похибка наближення функцii Вана промiжку Ваермiтовим сплайном з ланкою вигляду (40). В цьому випадку мiж параметрами наближень мають мiсце спiввiдношення;
Ва(41)
. (42)
Доведення. Сплайн з ланкою вигляду (39) характеризуiться системою рiвнянь
Ва(43)
а сплайн з ланкою вигляду (40) тАФ системою рiвнянь
Ва(44)
Надалi опускаiмо iндекс, який вказуi на приналежнiсть параметра до 
-i ланки. РЖз системи (44) при 
Ваматимемо
.
Подамо 
Ваяк 
, про логарифмуiмо це рiвняння i отримаiмо
,
де 
. Тобто при Варiвняння iз системи (44) зведене до рiвняння iз системи (43).
При 
рiвняння iз системи (44) маi вигляд
.
Помножимо чисельник i знаменник цього рiвняння на 
.
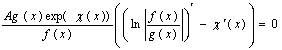Оскiльки з умов теореми 
Ване дорiвнюють нулю, то рiвнiсть досягаiться за умови, що
,
а це i i рiвняння iз системи (43) при .
Використовуючи метод математичноi iндукцii, покажемо, що рiвняння iз системи (44) зводиться до рiвнянь iз системи (43) за довiльних 
. Нехай це доведено для 
. Доведемо для 
. Рiвняння iз системи (43) при :
.
Для Варiвняння iз системи (44) маi вигляд
.
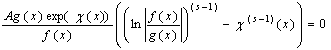Про диференцiюiмо це рiвняння i отримаiмо
Перший доданок в квадратних дужках дорiвнюi нулю через рiвнiсть нулю останнього спiвмножника. Рiвняння набере вигляду
.
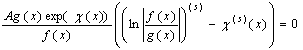Множник, який стоiть перед квадратними дужками, не дорiвнюi нулю з умов теореми, отже нулю дорiвнюi вираз у квадратних дужках. А це i i рiвняння iз системи (43). Отже, ми довели, що за довiльних Варiвняння в системах (43) i (44) еквiвалентнi, а , значить, i системи рiвносильнi. Тому 
Вапри 
, а 
.
Доведемо справедливiсть вiдношення (43) для похибок наближення. Оскiльки системи (43) i (44) рiвносильнi, то точки, в яких досягаiться максимальнi похибки, збiгаються. Нехай 
точка , в якiй досягаiться максимальна похибка наближення функцii 
Ваермiтовим сплайном з ланкою (39). Тодi похибка в цiй точцi дорiвнюi
.
РЖз цiii рiвностi випливаi, що
.
У правiй частинi маiмо вiдносну похибку наближення функцii Ваермiтовим сплайном з ланкою (40) на промiжку 
. Звiдси 
. Теорема доведена.
За допомогою цiii теореми можна отримувати наближення ермiтовим сплайном з ланкою (40) шляхом знаходження наближення ермiтовим сплайном з простiшою ланкою (39). Зокрема, наближення до функцii Ваермiтовим сплайном з ланкою вигляду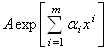
Вазводиться до наближення функцii 
Ваермiтовим сплайном з ланкою 
. При цьому найбiльша вiдносна похибка першого наближення виражаiться через найбiльшу абсолютну похибку другого наближення.
Теорема 2. Нехай для функцii 
Вапри Ваiснуi iдине наближення ермiтовим сплайном з непарною кiлькiстю параметрiв з вузлами Ваi ланками вигляду
Ва(45)
Тодi для функцii Вана промiжку Ваз тими ж вузлами iснуi iдине наближення ермiтовим сплайном з непарною кiлькiстю параметрiв i ланками вигляду
Ва(46)
Нехай ВатАФ найбiльша вiдносна похибка наближення функцii Вана промiжку Ваермiтовим сплайном з ланкою (45), а ВатАФ найбiльша вiдносна похибка наближення функцii Вана промiжку Ваермiтовим сплайном з ланкою вигляду (45). В цьому випадку мiж параметрами наближень мають мiсце спiввiдношення;
Ва(47)
.Ва (48)
Доведення. В теоремi 1 до системи рiвнянь (42) додаiться рiвняння
Ва, (49)
а до системи (43) рiвняння
Ва(50)
Для доведення цiii теореми для ермiтових сплайнiв з непарною кiлькiстю параметрiв необхiдно довести еквiвалентнiсть рiвнянь (48) i (50). Для цього перепишемо (50) у виглядi
.
Про логарифмуiмо i отримаiмо
,
де iз умови теореми 2 
, а 
.Тобто рiвняння (50) зведено до (49). Теорему доведено.
Властивiсть 1. Нехай при 
. Тодi
Ва(51)
Доведення. РЖз теорем 1 i 2 випливаi, що наближення функцii Вана 
Ваермiтовим сплайном з ланкою 
Ваможе бути знайдено через наближення функцii 
Вана цьому промiжку ермiтовим сплайном з ланкою . При цьому iз формули (42) випливаi, що максимальна вiдносна похибка 
Вапершого наближення виражаiться через максимальну абсолютну похибку 
другого наближення
РЖз рiвностi похибок i формули (37) матимемо
.
Цей вираз справедливий для довiльних Ва, Ваi промiжкiв Валише в тому випадку, якщо пiдiнтегральнi вирази рiвнi мiж собою. РЖз iх рiвностi випливаi вираз (51).
Тепер можна вивести аналiтичний вираз для ядра похибки наближення Ваермiтовим сплайном з ланкою (1). Ядро похибки наближення многочленом 
степеня 
маi вигляд 
. Застосувавши формулу (52), отримаiмо
Ва. (52)
Для ермiтового сплайна з експоненцiальною ланкою (6) ядро матиме такий вигляд:
.
А для ланки (13)
5. Рiвномiрне наближення ермiтовими сплайнами
Наближення функцii 
ермiтовим сплайном 
називаiмо рiвномiрним наближенням з заданою похибкою , якщо 
, де 
- вага наближення,
.
Алгоритм рiвномiрного наближення ермiтовими сплайнами з заданою похибкою. Алгоритм не залежить вiд виду сплайна.
1. Будуiмо ланку нелiнiйного ермiтового сплайна на всьому iнтервалi . Лiва границя 
Ваправа 
2. Знаходимо похибку наближення 
.
3. Якщо
, то наближення побудоване. Кiнець.
4. Якщо 
, то зсуваiмо праву границю iнтервалу влiво, поки похибка на даному iнтервалi не стане меншою вiд заданоi похибки . Допустимо, що при -му зсувi границi влiво (т. 
)похибка рiвна 
, а на попередньому кроцi 
( права границя 
). Тодi можна знайти таку праву границю 
, при якiй похибка 
Вабуде як завгодно мало вiдрiзнятися вiд заданоi 
. Точку 
Ваможна знайти одним iз вiдомих способiв, наприклад методом дiлення вiдрiзка навпiл або методом хорд.
5. ЗапамтАЩятовуiмо границi ланки i параметри ермiтового сплайна.
6. Лiвою границею наступноi ланки i права границя попередньоi ланки. Правою границею можна завжди вважати т. 
, але можна також екстраполювати точкою 
Ваде 
- довжина попередньоi ланки.
7. Будуiмо сплайн i знаходимо похибку.
8. Якщо , то переходимо до пункту 4.
9. ЯкщоВаi 
, то 
Ваi переходимо до пункту 7. В протилежному випадку, при 
, запамтАЩятовуiмо границi та параметри нелiнiйного ермiтового сплайна. Рiвномiрне наближення з заданою похибкою знайдено.
Очевидно, що описаний алгоритм приводить до iдиного рiшення, якщо наближувана функцiя Ваi сплайн такi що функцiя похибки
,
i неспадною функцiiю вiд . Для цього достатньо, щоб ядро наближення 
Вапри .
РЖз означення ермiтового сплайна можна запропонувати iнший алгоритм знаходження його параметрiв. При (парна кiлькiсть параметрiв) параметри визначаються iз тих же рiвнянь, що й у випадку фiксованих вузлiв, до яких додаються рiвняння для точки екстремуму
i правоi границi .
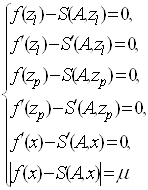Ва(53)
Потрiбно знайти залежнiсть Вавiд . Для деяких вузлiв ланок ермiтових сплайнiв, а саме ланок у виглядi многочлена, вiдношення многочлена до лiнiйноi функцii, добутку степеневоi i експоненцiальноi функцiй, степеневого виразу вiд многочлена параметри Васплайна знаходяться в аналiтичному виглядi iз перших чотирьох рiвнянь системи (53).
Вони залежать вiд 
Ваi значень функцii та ii похiдноi в цих точках. Коефiцiiнти можна пiдставити в птАЩяте i шосте рiвняння системи. В результатi система шести рiвнянь з шiстьома невiдомими зводиться до системи двох рiвнянь з двома невiдомими 
:
Ва(54)
Система (54) i системою трансцендентних рiвнянь. РЗi можна розвтАЩязати, використовуючи вiдомi наближенi методи знаходження коренiв трансцендентних систем.
Висновки
В багатьох технiчних задачах використовуiться кускова апроксимацiя однозначних функцiй. Застосування у такiй задачi нелiнiйних виразiв з метою наближення викликаi труднощi через вiдсутнiсть ефективних алгоритмiв для визначення iх параметрiв. Для цiii задачi i зручними кусковi наближення (сплайн-наближення). У роботi наведений приклад побудови ермiтового сплайна з експоненцiальною i многочленною ланками. Оскiльки похибка ермiтового сплайна з експоненцiальною ланкою в деяких випадках i меншою, нiж у многочленного ермiтового сплайна, то iх доцiльно застосовувати для наближення функцiй. Також побудовано алгоритми рiвномiрного наближення ермiтовими сплайнами.
Викладацька практика
1.10.2009 тАУ 3 пара.
Лекцiя з курсу "Теорiя масового обслуговування".
Тема: "Потоки Пальма".
Заняття проводилось для груп СРЖМ51 магiстри i спецiалiсти.
2.10.2009 тАУ 1 пара.
Лабораторна робота з курсу "Чисельнi методи".
Тема: "Однокроковi методи чисельного розвязування задачi Кошi для звичайних диференцiальних рiвнянь"
Заняття проводилось для групи ПМ41.
2.10.2009. тАУ 3 пара.
Практичне заняття з курсу "Теорiя масового обслуговування".
Тема: "Найпростiший потiк"
Заняття проводилось для груп СРЖМ51 магiстри i спецiалiсти.
Опис програми
Програма HermitтАЩs spline шукаi балансне наближення функцiй ермiтовими сплайнами. Головне вiкно програми роздiлене на двi частини: лiву i праву. У лiвiй частинi i три закладки: перша призначена для виводу результатiв програми, друга для виводу графiкiв функцii i сплайну; третя для виводу графiку похибки наближення. У правiй частинi i поля для вводу меж iнтервалу i похибки. Також i перемикачi для вибору виду сплайна i функцii.
Для роботи програми треба виконати наступнi дii:
В· у поля "2" "3" потрiбно ввести межi iнтервалу на якому функцiя визначена i диференцiйовна;
В· у поле "1" треба ввести похибку;
В· вибрати вид сплайна 4;
В· вибрати функцiю 5;
В· далi натиснути кнопку "6", яка викликаi функцiю, що будуi балансне наближення iз заданою похибкою;
В· для побудови балансного наближення iз заданою кiлькiстю ланок треба натиснути кнопку "8";
В· вивiд результатiв буде у полi "7";
В· щоб переглянути графiки функцii i сплайну потрiбно натиснути на закладку 9;
В· щоб переглянути графiк похибки наближення потрiбно натиснути на закладку 10;
Опис основних функцiй програми:
В· void ermit_1(double *a, double x0, double x1); - функцiя пошуку коефiцiiнтiв ермiтового сплайна з ланками виду 
;
В· void ermit_2(double *a, double x0, double x1); - функцiя пошуку коефiцiiнтiв ермiтового сплайна з ланками виду 
;
В· void ermit_3(double *a, double x0, double x2); - функцiя пошуку коефiцiiнтiв ермiтового сплайна з ланками виду ;
В· void ermit_4(double *b, double x0, double x2); - функцiя пошуку коефiцiiнтiв ермiтового сплайна з ланками виду 
;
В· void ermit_5(double *a, double zl, double zp); - функцiя пошуку коефiцiiнтiв ермiтового сплайна з ланками виду
;
В· void ermit_rp(double *a, double a1, double b1, double nyu, int n); - рiвномiрне наближення ермiтовими сплайнами iз заданною похибкою;
В· void ermit_rl (double*a, double zl, double b1, int n, int p, int r); - рiвномiрне наближення ермiтовими сплайнами iз заданною кiлькiстю ланок.
Лiтература
1. Пiзюр Я.В., Попов Б.О. Рiвномiрне наближення ермiтовими сплайнами з парною кiлькiстю параметрiв.// Контрольно-вимiрювальна технiка.- 1993. тАУ Вип. 50. тАУ С. 8-13
2. Пiзюр Я.В. Наближення функцiй ермiтовими сплайнами з експоненцiальними ланками// Вiсник НУ "Львiвська полiтехнiка". "Фiзико-математичнi науки" №566, 2006, тАУ С. 68-75.
3. ЗавтАЩялов Ю.С., Квасов Б.И., Мiрошниченко В.Л. Методи сплайн функцiй. тАУ М.: Наука, 1980. тАУ 352 с.
Додаток
Код програми.
private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
double zl, zp, x;
zl=Double::Parse(textBox3->Text);
zp=Double::Parse(textBox4->Text);
x =(zl+zp)/2;
int p=2,n=5;
if((s1->Checked==true)||(s2->Checked==true)||(s5->Checked==true)||(s7->Checked==true)||(s9->Checked==true)){
n=4;p=1;
}
double *a = new double[n];
if (s1->Checked == true) {
ermit_1(a, zl, zp, p);
}
if (s2->Checked == true) {
ermit_2(a, zl, zp, p);
}
if (s3->Checked == true) {
ermit_3(a, zl, zp, p);
}
if (s4->Checked == true) {
ermit_4(a, zl, zp, p);
}
if (s5->Checked == true) {
ermit_5(a, zl, zp, p);
}
if (s6->Checked == true) {
ermit_6(a, zl, zp, p);
}
if (s7->Checked == true) {
ermit_8(a, zl, zp, p);
}
if (s8->Checked == true) {
ermit_9(a, zl, zp, p);
}
if (s9->Checked == true) {
ermit_7(a, zl, zp, p);
}
chart1->Series["Function"]->Points->Clear();
chart1->Series["Spline"]->Points->Clear();
chart2->Series["error"]->Points->Clear();
double t,ch1,ch2,ch3;
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,1);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
double epx_p(double *a, double x, int p) {
return Math::Abs((f(x, p) - sp(a, x)) / w(x));
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
public: double f(double x, int p) {
if(f1->Checked==true){
return Math::Sin(x);
}
if(f2->Checked==true){
return Math::Cos(x);
}
if(f3->Checked==true){
return 1 / (2 + x * x);
}
if(f4->Checked==true){
return Math::Log(x + 1);
}
if(f5->Checked==true){
return Math::Exp(x);
}
if(f6->Checked==true){
return x*x;
}
return -1;
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
public: double fp(double x, int p) {
if(f1->Checked==true){
return Math::Cos(x);
}
if(f2->Checked==true){
return -Math::Sin(x);
}
if(f3->Checked==true){
return (-2* x ) / ((2 + x * x) * (2 + x * x));
}
if(f4->Checked==true){
return 1 / (x + 1);
}
if(f5->Checked==true){
return Math::Exp(x);
}
if(f6->Checked==true){
return 2*x;
}
return -1;
}
//*****************************************
public: void ermit_1(double *a, double x0, double x1, int p) {
a[3] = (fp(x1, p) / f(x1, p) + fp(x0, p) / f(x0, p) + 2 * (Math::Log(f(x0, p)
/ f(x1, p)) / (x1 - x0))) / ((x1 - x0) * (x1 - x0));
a[2] = ((2* x0 * x0 - x0 * x1 - x1 * x1) * a[3] - (fp(x0, p) / f(x0, p))
- (Math::Log(f(x0, p) / f(x1, p)) / (x1 - x0))) / (x1 - x0);
a[1] = (1 / (x1 - x0)) * (Math::Log(f(x1, p) / f(x0, p)) - a[3] * (x1 * x1 * x1
- x0 * x0 * x0) - a[2] * (x1 * x1 - x0 * x0));
a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0));
}
/////////////////////////////////////////////////////////////////////////////
void ermit_2(double *b, double x0, double x1, int p) {
double h;
h = x1 - x0;
b[3] = 2 * ((fp(x1, p) + fp(x0, p)) / 2 - (f(x1, p) - f(x0, p)) / h) / (h
* h);
b[2] = 0.5 * ((fp(x1, p) - fp(x0, p)) / h - 3* b [3] * (x0 + x1));
b[1] = fp(x1, p) - 2* b [2] * x1 - 3* b [3] * x1 * x1;
b[0] = 0.5 * (f(x1, p) + f(x0, p) - b[3] * (x0 * x0 * x0 + x1 * x1 * x1)
- b[2] * (x0 * x0 + x1 * x1) - b[1] * (x0 + x1));
}
////////////////////////////////////////////////////////////////
void ermit_3(double *a, double x0, double x2, int p) {
double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;
double x1;
x1 = (x0 + x2) / 2;
a1 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - Math::Log(f(x2, p) / f(x0, p)) / (x2 - x0);
b1 = (x1 + x0) * (x1 * x1 + x0 * x0) - (x2 + x0) * (x2 * x2 + x0 * x0);
z1 = x1 * x1 + x1 * x0 - x2 * x2 - x2 * x0;
g1 = x1 - x2;
a2 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x0, p) / f(x0, p);
b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;
z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;
g2 = x1 - x0;
a3 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x2, p) / f(x2, p);
b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;
z3 = x1 * x1 + x0 * x1 + x0 * x0 - 3* x2 * x2;
g3 = x1 + x0 - 2* x2 ;
a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)
* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)
+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));
a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1 * b2);
a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;
a[1] = (1 / (x2 - x0)) * (Math::Log(f(x2, p) / f(x0, p)) - a[4] * (x2 * x2 * x2
* x2 - x0 * x0 * x0 * x0) - a[3] * (x2 * x2 * x2 - x0 * x0 * x0)
- a[2] * (x2 * x2 - x0 * x0));
a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0 + a[4] * x0 * x0 * x0 * x0));
}
///////////////////////////////////////////////////////////////////////////
void ermit_4(double *a, double x0, double x2, int p) {
double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;
double x1, h;
x1 = (x0 + x2) / 2;
h = x1 - x0;
a1 = (f(x2, p) - f(x0, p)) / (x2 - x0) - (f(x1, p) - f(x0, p)) / (x1 - x0);
b1 = (x2 + x0) * (x2 * x2 + x0 * x0) - (x1 + x0) * (x1 * x1 + x0 * x0);
z1 = x2 * x2 + x2 * x0 - x1 * x1 - x1 * x0;
g1 = x2 - x1;
a2 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x0, p);
b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;
z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;
g2 = x1 - x0;
a3 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x2, p);
b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;
z3 = (x1 * x1 + x0 * x1 + x0 * x0) - 3* x2 * x2;
g3 = (x1 + x0 - 2* x2 );
a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)
* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)
+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));
a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1
* b2);
a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;
a[1] = (f(x1, p) - f(x0, p)) / h - a[2] * (x1 + x0) - a[3] * (x1 * x1 + x1
* x0 + x0 * x0) - a[4] * (x1 + x0) * (x1 * x1 + x0 * x0);
a[0] = f(x0, p) - a[1] * x0 - a[2] * x0 * x0 - a[3] * x0 * x0 * x0 - a[4]
* x0 * x0 * x0 * x0;
}
////////////////////////////////////////////////////////////////
void ermit_5(double *a, double zl, double zp, int p) {
double h, x1;
h = (zp - zl) / 2;
x1 = (zp + zl) / 2;
a[3] = ((h * h * (fp(zp, p) - fp(zl, p))) / (f(zp, p) - f(zl, p) - h * (fp(
zp, p) + fp(zl, p)))) - x1;
a[2] = ((fp(zp, p) - fp(zl, p)) * (((x1 + a[3]) * (x1 + a[3]) - h * h)
* ((x1 + a[3]) * (x1 + a[3]) - h * h))) / (4* h * (x1 + a[3]));
a[0] = fp(zl, p) + a[2] / ((x1 + a[3] - h) * (x1 + a[3] - h));
a[1] = f(zl, p) - a[0] * (x1 - h) - a[2] / (x1 - h + a[3]);
}
////////////////////////////////////////////////////////////////////
void ermit_8(double *a, double zl, double zp, int p) {
double j0, j1, j2, m0, m1;
j0 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p))) / (zp - zl);
j1 = (zl * zl - zp * zp) / (zp - zl);
j2 = (zl * zl * zl - zp * zp * zp) / (zp - zl);
m0 = (f(zl, p) * Math::Exp(f(zl, p)) - j0) / (j1 - 2* zl );
m1 = (2* zl * zl - j2) / (j1 - 2* zl );
a[3] = (-fp(zp, p) * Math::Exp(f(zp, p)) + j0 + m0 * j1 - 2* zp * m0) / (3* zp
* zp + 2* zp * m1 - j2 - m1 * j1);
a[2] = m0 + a[3] * m1;
a[1] = j0 + j1 * a[2] + a[3] * j2;
a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl;
}
///////////////////////////////////////////////////////////////////
void ermit_9(double *a, double zl, double zp, int p) {
double j1, j2, j3, j4, m1, m2, m3, k1, k2, z;
z = (zp + zl) / 2;
j1 = (zp * zp - z * z) / (z - zp);
j2 = (zp * zp * zp - z * z * z) / (z - zp);
j3 = (zp * zp * zp * zp - z * z * z * z) / (z - zp);
j4 = (Math::Exp(f(z, p)) - Math::Exp(f(zp, p))) / (z - zp);
m1 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p)) + j4 * (zl - zp)) / (zp * zp - zl * zl + j1 * (zp - zl));
m2 = (zl * zl * zl - zp * zp * zp + j2 * (zl - zp)) / (zp * zp - zl * zl
+ j1 * (zp - zl));
m3 = (zl * zl * zl * zl - zp * zp * zp * zp + j3 * (zl - zp)) / (zp * zp
- zl * zl + j1 * (zp - zl));
k1 = (Math::Exp(f(zl, p)) * fp(zl, p) - j4 - m1 * j1 - 2* zl * m1) / (j2 + 3* zl
* zl + j1 * m2 + 2* m2 * zl);
k2 = (j3 + 4* zl * zl * zl + j1 * m3 + 2* m3 * zl) / (j2 + 3* zl * zl + j1
* m2 + 2* m2 * zl);
a[4] = (Math::Exp(f(zp, p)) * fp(zp, p) - j4 - m1 - j1 - 2* zp * m1 - k1 * j2
- 3* zp * zp * k1 - k1 * j1 * m2 - 2* m2 * zp * k1) / (j3 + 4* zp
* zp * zp + j1 * m3 + 2* m3 * zp - k2 * j2 - 3* zp * zp * k2 - k2
* j1 * m2 - 2* m2 * zp * k2);
a[3] = k1 - k2 * a[4];
a[2] = m1 + a[3] * m2 + a[4] * m3;
a[1] = j4 + a[2] * j1 + a[3] * j2 + a[4] * j3;
a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl
- a[4] * zl * zl * zl * zl;
}
///////////////////////////////////////////////////////////////////
double poldiv_p3(double*a, double zl, double b1, int n, int p) {
double zp, ny, x, nyu,ny1,ny2, x1, x2;
textBox2->Text="";
nyu=Double::Parse(textBox1->Text);
String ^ path = Path::GetFileName("rez.txt");
FileInfo^ fi = gcnew FileInfo(path);
StreamWriter ^ sw = fi->CreateText();
int l = 0;
double t,ch1,ch2,ch3;
chart1->Series["Function"]->Points->Clear();
chart1->Series["Spline"]->Points->Clear();
chart2->Series["error"]->Points->Clear();
zp = zl + 0.00510101101;;
while (1) {
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики