Элементы тензороного исчисления
Возникновение тензорного исчисления было подготовлено в 19 веке развитием теории алгебраических форм, с одной стороны, и теории квадратичных дифференциальных форм - с другой. Исследования в области теории дифференциальных квадратичных форм были непосредственно связаны с дифференциальной геометрией: с геометрией поверхностей (К. Гаусс) и с геометрией многомерного метрического пространства (Б. Риман). Современную форму тензорному исчислению придал итальянский математик Г. Риччи-Курбастро, поэтому тензорное исчисление иногда называется исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915-16) общей теории относительности А. Эйнштейна, математическая часть которой целиком основана на тензорном исчислении.
Тензор (от лат. tensus - напряжённый, натянутый), математический термин, появившийся в середине 19 века и с тех пор применяющийся в двух различных смыслах. Наибольшее распространение термин ВлтензорВ» получил в современном тензорном исчислении, где это название присваивается особого рода величинам, преобразующимся по особому закону. В механике, особенно в теории упругости, термин ВлтензорВ» широко применяется как синоним симметрического аффинора, то есть линейного оператора F, преобразующего вектор х в вектор Fх, и симметрического в том смысле, что скалярное произведение уFх не меняется при перестановке векторов х и у. Здесь термин был первоначально связан с малыми растяжениями (и сжатиями), возникающими при упругой деформации (откуда и название ВлтензорВ»), а затем перенесён в другие области механики. Так появились тензор деформации, тензор напряжения, тензор инерции и др.
Вз1. Линейные преобразования
Пусть переменные 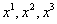 Вапреобразуются в новые
Вапреобразуются в новые 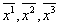 Вас помощью линейного преобразования
Вас помощью линейного преобразования
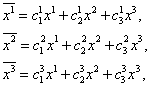
где 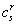 Ва- константы (все индексы пробегают значения 1, 2, 3.., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
Ва- константы (все индексы пробегают значения 1, 2, 3.., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
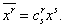 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.1)
Мы предполагаем, что определитель преобразования 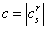 Ване равен нулю. Пусть
Ване равен нулю. Пусть 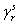 Ваявляется алгебраическим дополнением элемента
Ваявляется алгебраическим дополнением элемента 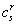 Вав определителе c деленным на величину
Вав определителе c деленным на величину 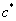 (
(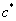 - обратная матрица). Тогда
- обратная матрица). Тогда
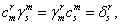 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.2)
и мы можем разрешить систему уравнений (1.1) относительно x
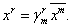 ВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.3)
ВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.3)
Это показывает, что данное преобразование обратимо.
Кроме того, если 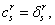 Вамы имеем
Вамы имеем
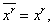
т. е. тождественное преобразование.
Если перейти сначала от переменных 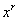 к
к 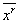 по (1.1), а затем от переменных
по (1.1), а затем от переменных 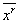 к
к 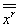 при помощи преобразования
при помощи преобразования
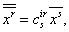
то мы видим, что переход от первоначальных переменных 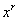 Вак
Вак 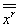 определяется формулой
определяется формулой
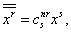
где
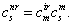
Это преобразование, следовательно, также линейное.
Говорят, что совокупность преобразований образует группу, когда она удовлетворяет следующим условиям: 1) если преобразования от 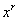 к
к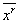 и от
и от 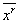 к
к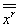 принадлежат данной совокупности, то преобразование от
принадлежат данной совокупности, то преобразование от 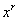 к
к 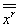 также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
Таким образом, совокупность линейных преобразований образует группу.
Вз 2. Индексные обозначения
Если нам дана совокупность трех независимых переменных, то они могут быть обозначены тремя различными буквами, например x,y,z, но мы считаем более удобным обозначать переменные данной совокупности одной и той же буквой, различая их посредством индексов. Таким образом, мы можем записать три переменные в виде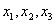 , или в более компактной форме:
, или в более компактной форме:
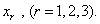 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.1)
Здесь мы написали индекс внизу, но в равной мере мы могли бы использовать вместо этого верхний значок, так что переменные были бы записаны в виде 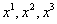 Ваили
Ваили
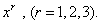 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.2)
Однородная линейная функция переменных обычно записывается в виде
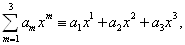 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
где 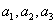 Ва- константы. Таким образом, коэффициенты линейной формы могут быть записаны в виде
Ва- константы. Таким образом, коэффициенты линейной формы могут быть записаны в виде
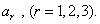
Объекты, которые, подобно 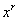 и
и 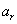 , зависят только от одного индекса, называются объектами первого порядка, а отдельные буквы с индексами
, зависят только от одного индекса, называются объектами первого порядка, а отдельные буквы с индексами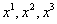 и
и 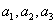 Ваназываются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовем трехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов
Ваназываются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовем трехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов
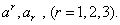 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)
С другой стороны, однородная квадратичная функция трех переменных имеет вид
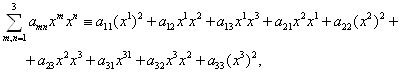 ВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)
где атп - константы. Мы видим, что коэффициенты квадратичной формы зависят от двух индексов и записываются так:
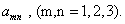
Составляющие этого объекта преобразуются следующим образом:
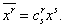
Следовательно, эта формула дает один из способов, с помощью которого может быть преобразован объект первого порядка. Любой объект, составляющие которого преобразуются по этому закону, называется контравариантным вектором. Таким образом, есть контравариантный вектор, если при линейном преобразовании переменных (1.1) его преобразованные составляющие определяются формулами
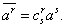 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.6)
Имеется и другой способ преобразования элементов объекта первого порядка. Мы уже видели, что коэффициенты линейной формы переменных x также образуют объект первого порядка. Таким образом, коэффициенты линейной формы 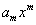 Ваявляются составляющими объекта
Ваявляются составляющими объекта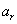 . Предположим, что составляющие
. Предположим, что составляющие 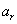 Вапреобразуются таким образом, что линейная форма
Вапреобразуются таким образом, что линейная форма 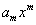 Ваостается инвариантной относительно преобразования переменных (1.1). Если мы обозначим через
Ваостается инвариантной относительно преобразования переменных (1.1). Если мы обозначим через 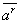 новые составляющие объекта
новые составляющие объекта 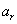 Ва(после преобразования), то получим
Ва(после преобразования), то получим
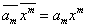 ,
,
так как эта линейная форма есть инвариант. Тогда из (1.3) следует
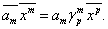
Поскольку немой индекс может быть обозначен любой буквой, то эту систему уравнений можно записать в виде
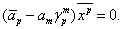
Если это соотношение справедливо для всех значений переменных 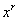 , то должно выполняться равенство
, то должно выполняться равенство
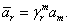 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.7)
Это преобразование, очевидно, отлично от преобразования, задаваемого формулой (2.6). Объект первого порядка, составляющие которого преобразуются по этому закону, называется ковариантным вектором.
Таким образом, у нас есть два типа тензоров первого порядка, и мы условимся различать их с помощью положения индекса. Если - тензор контравариантен, мы используем верхний индекс, если же он ковариантен, то нижний. Другими словами, верхний индекс обозначает контравариантностъ, а нижний индекс тАФ ковариантность.
Объекты, которые зависят от двух индексов, называются объектами второго порядка. Из того, что индексы бывают верхние и нижние, следует, что объекты второго порядка могут быть трех типов:
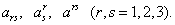 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.8)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.8)
Легко видеть, что в этом случае каждый объект имеет 9 составляющих.
Аналогично можно получить объекты третьего порядка, которые будут зависеть от трех индексов и могут принадлежать к любому из четырех типов:
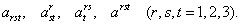 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.9)
Здесь каждый объект содержит 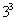 или 27 составляющих. Мы можем продолжать это построение и получить объекты любого порядка.
или 27 составляющих. Мы можем продолжать это построение и получить объекты любого порядка.
Для законченности этой последовательности мы назовем объект а, не имеющий индексов, объектом нулевого порядка. Если этот объект имеет одно и то же значение и в новых переменных 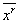 Ваи в старых переменных
Ваи в старых переменных 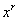 , то он называется скаляром, или инвариантом. Следовательно, если а есть инвариант, то
, то он называется скаляром, или инвариантом. Следовательно, если а есть инвариант, то
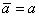 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)
где 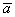 Ваесть значение данного объекта в новых переменных.
Ваесть значение данного объекта в новых переменных.
Мы взяли число измерений равным трем лишь для определенности. Все, что было сказано выше, применимо также к любому числу измерений, если условиться, что число значений, пробегаемых индексом, равно числу измерений. Например, если число измерений равно четырем, следует считать, что индексы могут пробегать значения от 1 до 4, а не от 1 до 3, как предполагалось выше.
Вз 3. Общее определение тензоров
Векторы, ковекторы, линейные операторы, и билинейные формы - примеры тензоров. Они являются геометрическими объектами, которые представляются в числовой форме, после того, как выбран базис в пространстве. Это числовое представление является своим для каждого из них: векторы и ковекторы представляются одномерными массивами, линейные операторы и квадратичные формы - двумерными массивами. Кроме количества индексов, имеет значение также и их расположение. Координаты вектора нумеруются одним верхним индексом, который называется контравариантным индексом. Координаты ковектора нумеруются одним нижним индексом, который называется ковариантным индексом. В матрице билинейной формы мы используем два нижних индекса; поэтому билинейные формы называют дважды-ковариантными тензорами. Линейные операторы - тензоры смешанного типа; их элементы нумеруются одним нижним и одним верхним индексами. Число индексов и их положения определяют правила преобразования, т.е. то как компоненты каждого конкретного тензора ведут себя при смене базиса. В общем случае, любой тензор представляет собой многомерный массив с определенным числом верхних и нижних индексов. Давайте обозначать число этих индексов через r и . Тогда получится тензор типа (r,); или иногда используется термин валентность. Тензор типа (r,), или тензор валентности (r,) - это r-раз контравариантный и s-раз ковариантный тензор.
Все это была терминология; теперь давайте перейдем к точному определению.
Оно базируется на следующих общих формулах преобразования:
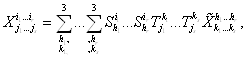 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.1)
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.2)
Определение 1. Геометрический объект X, который в каждом базисе представляется (r + )-мерным массивом 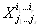 вещественных чисел, удовлетворяющих правилам преобразования (3.1) и (3.2) при смене базиса, называется тензором типа (r,), или валентности (r,).
вещественных чисел, удовлетворяющих правилам преобразования (3.1) и (3.2) при смене базиса, называется тензором типа (r,), или валентности (r,).
Индексы 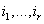 Ваи
Ваи 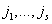 - свободные индексы. В правой стороне равенства (3.1) они распределены в S-ках и T-шках, каждый имеет только одно вхождение и сохраняет свою позицию при переходе из левой в правую часть равенства, т.е. верхние индексы
- свободные индексы. В правой стороне равенства (3.1) они распределены в S-ках и T-шках, каждый имеет только одно вхождение и сохраняет свою позицию при переходе из левой в правую часть равенства, т.е. верхние индексы 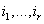 Ваостаются верхними, а нижние индексы
Ваостаются верхними, а нижние индексы 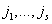 остаются нижними в правой части равенства (3.1).
остаются нижними в правой части равенства (3.1).
Остальные индексы 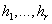 Ваи
Ваи 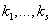 Ва- это индексы суммирования, они входят в правую часть (3.1) парами: один раз в качестве верхнего индекса и один раз в качестве нижнего индекса, один раз в S-матрице либо в T-матрице и второй раз среди индексов в компонентах массива
Ва- это индексы суммирования, они входят в правую часть (3.1) парами: один раз в качестве верхнего индекса и один раз в качестве нижнего индекса, один раз в S-матрице либо в T-матрице и второй раз среди индексов в компонентах массива 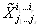 .
.
При выражении 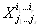 Вачерез
Вачерез 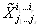 Вакаждый верхний индекс обслуживается ровно один раз матрицей прямого перехода S, порождая при этом ровно одно суммирование в формуле (3.1):
Вакаждый верхний индекс обслуживается ровно один раз матрицей прямого перехода S, порождая при этом ровно одно суммирование в формуле (3.1):
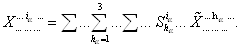 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.3)
Подобным же образом, каждый нижний индекс обслуживается матрицей обратного перехода T и тоже порождает одно суммирование в формуле (1):
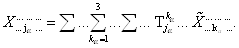 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.4)
Формулы (3.3) и (3.4) совпадают с (3.1), они записаны для того, чтобы сделать более понятным то, как записывается формула (3.1). Итак, определение тензоров дано.
Вз 4. Скалярное произведение и метрический тензор
Ковекторы, линейные операторы и билинейные формы, те, что мы рассматривали выше, все это были искусственно построенные тензоры. Однако, есть некоторое количество тензоров естественного происхождения. Давайте вспомним, что мы живем в метрическом мире. Мы можем измерять расстояния между точками (следовательно, мы можем измерять длины векторов) и измерять углы между двумя направлениями в пространстве. Поэтому для любых двух векторов x и y мы можем определить их скалярное произведение:
(x,y) = |xycos(φ), ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.1)
где φ - угол между векторами x и y. Это естественное скалярное произведение, порожденное нашей способностью измерять длины или, вернее сказать, тем, что понятие длины дано нам в ощущениях в том мире, где мы живем.
Вспомним следующие свойства естественного скалярного произведения (4.1):
(1) (x+y, z) = (x, z)+(y, z);
(2) (αx, y) = α(x, y);
(3) (x, y+z) = (x, y)+(x, z);
(4) (x, αy) = α(x, y);
(5) (x, y) = (y, x);
(6) (x, x)≥0 и (x, x) = 0 влечетx = 0.
Обратите внимание, что первые четыре свойства скалярного произведения
(4.1) очень похожи на свойства квадратичной формы. Это не случайное совпадение.
Давайте рассмотрим два произвольных вектора x и y вместе с их разложениями в некотором базисе 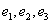 . Это означает, что мы имеем следующие выражения для них:
. Это означает, что мы имеем следующие выражения для них:
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.2)
Подставим (4.2) в формулу (4.1) и, используя четыре свойства(1)тАУ(4) из шести упомянутых в упражнении, выведем следующую формулу для скалярного произведения векторов x и y:
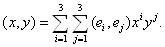 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.3)
Обозначим 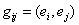 Ваи запишите (4.3) в виде
Ваи запишите (4.3) в виде
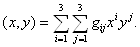 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.4)
Рассмотрим другой базис 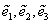 , обозначим
, обозначим 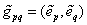 Ваи посредством формул преобразования
Ваи посредством формул преобразования
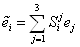 и
и 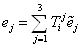
докажем, что матрицы 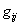 и
и 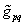 являются компонентами геометрического объекта, подчиняющимися преобразованиям
являются компонентами геометрического объекта, подчиняющимися преобразованиям
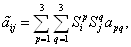 Ваи
Ваи 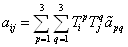
при замене базиса. Таким образом мы докажем, что эта матрица Грама
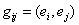 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.5)
задает тензор типа (0,2). Это очень важный тензор; его называют метрическим тензором. Оно описывает не только скалярное произведения в форме (4.4), но и всю геометрию нашего пространства. Свидетельства этого факта приводятся ниже.
Матрица (4.5) симметрична из-за свойства (5). Теперь, сравнивая формулу (4.4) с формулой

и помня о тензорной природе матрицы (4.5), мы приходим к выводу, что скалярное произведение тАУ это симметричная билинейная форма:
(x, y) = g(x,y). ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.6)
Квадратичная форма, соответствующая (4.6), очень проста: f(x) = g(x,x) =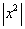 . Обратная матрица для (4.5) обозначается тем же самым символом g, но она имеет два верхних индекса:
. Обратная матрица для (4.5) обозначается тем же самым символом g, но она имеет два верхних индекса: 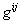 . Это определяет тензор типа (2,0). Такой тензор называется дуальным метрическим тензором.
. Это определяет тензор типа (2,0). Такой тензор называется дуальным метрическим тензором.
Вз5. Действия с тензорами
1)ВаВаВаВаВа Линейные операции.
Так как 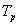 Ва- пространство тензоров ранга р - является линейным пространством, то в нем определены действия сложения и умножения на число:
Ва- пространство тензоров ранга р - является линейным пространством, то в нем определены действия сложения и умножения на число:
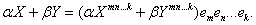 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.1)
Если тензоры представлены своими компонентами в одном и том же базисе, то линейной комбинации тензоров соответствует та же линейная комбинация их компонент.
2)ВаВаВаВаВа Тензорное умножение.
В отличие от линейных операций, это действие совершается с произвольными тензорами, не обязательно имеющими одинаковый ранг.
Если X - тензор ранга р, а Y - тензор ранга q, то результатом будет тензор ранга +q, обозначаемый XY:
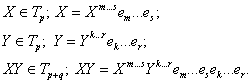 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.2)
Тензорное произведение произвольного числа тензоров обладает свойством ассоциативности.
Для того чтобы перейти к другим действиям с тензорами, нам понадобится следующее определение.
Определение. Тензоры, представимые в виде abcтАжh, называются разложимыми.
Не каждый тензор является разложимым, но любой тензор может быть представлен в виде линейной комбинации разложимых.
3)ВаВаВаВаВа Перестановка (i,j).
Перестановкой T(i,j) называется линейная функция, действующая из 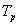 Вав
Вав 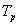 Ва(т.е. не меняющая ранг тензора) и состоящая для разложимых тензоров во взаимной перестановке векторов, стоящих на i-м и j-м местах:
Ва(т.е. не меняющая ранг тензора) и состоящая для разложимых тензоров во взаимной перестановке векторов, стоящих на i-м и j-м местах:
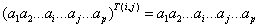 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(5.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(5.3)
Например,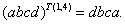
На произвольные тензоры операция перестановки распространяется по линейности, например:
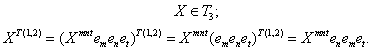
Для тензоров второго ранга возможна только одна перестановка - Т(1,2), обозначаемая просто буквой Т:
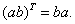
Для произвольного тензора второго ранга X имеем:
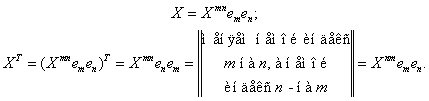
Из полученного соотношения для 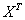 Вавидно, что матрица компонент тензора
Вавидно, что матрица компонент тензора 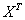 в простом базисе является транспонированной матрицей компонент тензора X в том же базисе. Именно поэтому операция перестановки тензоров второго ранга называется еще транспонированием.
в простом базисе является транспонированной матрицей компонент тензора X в том же базисе. Именно поэтому операция перестановки тензоров второго ранга называется еще транспонированием.
4) Свертывание (i,j).
Свертыванием 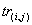 Ваназывается линейная функция, действующая из
Ваназывается линейная функция, действующая из 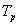 в
в 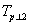 Ва(понижающая ранг тензора на 2) и состоящая для разложимых тензоров в скалярном перемножении вектора, занимающего i-е место, на вектор, занимающий j-е место:
Ва(понижающая ранг тензора на 2) и состоящая для разложимых тензоров в скалярном перемножении вектора, занимающего i-е место, на вектор, занимающий j-е место:
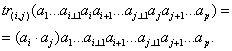 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.4)
Например, 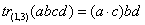 .
.
На произвольные тензоры операция свертывания переносится по линейности, например:
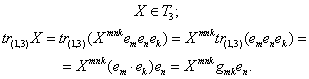
Для тензоров второго ранга возможно только одно свертывание - 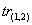 , обозначаемое просто
, обозначаемое просто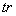 :
:
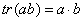
Скаляр 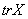 Ваназывается следом тензора второго ранга X.
Ваназывается следом тензора второго ранга X.
Если тензор записан в смешанных компонентах, то
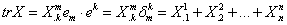
(п - размерность пространства Эп). Таким образом, след тензора второго ранга совпадает со следом матрицы его смешанных компонент.
Для матриц ко- или контравариантных компонент предыдущее утверждение, вообще говоря, не верно:
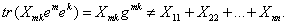
5)ВаВаВаВаВа Простое умножение.
Простым умножением тензора X ранга р на тензор Y ранга q называется операция, состоящая в свертывании (р,р + 1) тензорного произведения XY и обозначаемая 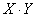 :
:
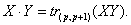 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.5)
Другими словами, простое умножение сводится к скалярному перемножению последних векторов в разложении тензора X на первые векторы в разложении тензора Y. Для разложимых тензоров:
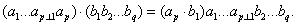
Для произвольных тензоров:
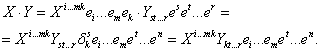
В результате простого умножения тензора ранга р на тензор ранга q получается тензор ранга р+q-2. В частности, результатом простого умножения двух тензоров второго ранга будет тензор второго ранга.
6)ВаВаВаВаВа Косое умножение.
Это действие имеет смысл только для тензоров, построенных на основе трехмерного векторного пространства  . Как уже упоминалось, в
. Как уже упоминалось, в 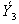 определено векторное произведение векторов
определено векторное произведение векторов 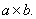
Пусть 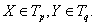 Операция косого умножения, обозначаемая
Операция косого умножения, обозначаемая 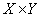 , приводит к тензору ранга р+q-1 и состоит в векторном перемножении последних векторов в разложении тензора X на первые векторы в разложении тензора Y:
, приводит к тензору ранга р+q-1 и состоит в векторном перемножении последних векторов в разложении тензора X на первые векторы в разложении тензора Y:
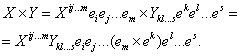 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (5.6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (5.6)
Очевидно, что в случае двух векторов операция косого умножения совпадает с векторным умножением.
Для тензоров второго ранга с использованием векторного умножения строится еще одна операция - векторный инвариант. Это унарная (т.е. имеющая один аргумент) операция, применительно к тензору T обозначаемая как Тх, определяется для разложимых тензоров следующим образом
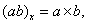 ,
,
и распространяется на произвольные тензоры по линейности:
7) Полное умножение.
Пусть  , причем р>q.
, причем р>q.
Операцию полного умножения, обозначаемую 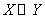 , определим сначала для разложимых тензоров следующим образом: при полном умножении (разложимого) тензора X на тензор Y производится скалярное умножение последнего вектора в разложении тензора X на последний вектор в разложении тензора Y, затем скалярное умножение предпоследних векторов в разложениях этих тензоров и т.д., пока не будут исчерпаны все векторы в разложении тензора Y:
, определим сначала для разложимых тензоров следующим образом: при полном умножении (разложимого) тензора X на тензор Y производится скалярное умножение последнего вектора в разложении тензора X на последний вектор в разложении тензора Y, затем скалярное умножение предпоследних векторов в разложениях этих тензоров и т.д., пока не будут исчерпаны все векторы в разложении тензора Y:
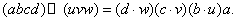 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5.7)
Для произвольных тензоров полное умножение производится по правилу "многочлен на многочлен". Результатом полного умножения тензора ранга р на тензор ранга q является тензор ранга р -q.
Если X и Y - тензоры одинакового ранга, то полное умножение 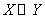 совпадает с введенным ранее скалярным произведением в пространстве
совпадает с введенным ранее скалярным произведением в пространстве 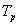 .
.
Вз6. Поднятие и опускание индексов
Предположим, что X - это тензор типа (r,s). Давайте выберем его α-тый нижний индекс: 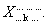 ВаСимволы, используемые для других индексов, несущественны. Поэтому, мы обозначили их точками. Затем рассмотрим тензорное произведение
ВаСимволы, используемые для других индексов, несущественны. Поэтому, мы обозначили их точками. Затем рассмотрим тензорное произведение 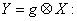
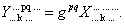 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.1)
Здесь g - дуальный метрический тензор с элементами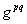 . На следующем шаге свернем (6.1) по паре индексов k и q. Для этой цели мы заменяем их на и проводим суммирование:
. На следующем шаге свернем (6.1) по паре индексов k и q. Для этой цели мы заменяем их на и проводим суммирование:
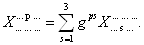 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.2)
В целом вся операция (6.2) называется поднятием индекса. Эта операция обратима. Обратная операция называется опусканием индексов:
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.3)
Подобно (6.2), операция опускания индекса (6.3) включает в себя две операции над тензорами: тензорное произведение и свертку.
Вз7.Тензоры в криволинейных координатах
Мы будем рассматривать область 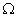 Вааффинного пространства, отнесенную к криволинейным координатам
Вааффинного пространства, отнесенную к криволинейным координатам 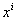 . Радиус-вектор х произвольной точки М области
. Радиус-вектор х произвольной точки М области 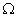 , отсчитываемый от фиксированной точки О, будет выражаться функцией
, отсчитываемый от фиксированной точки О, будет выражаться функцией
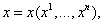 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.1)
достаточное число раз непрерывно дифференцируемой. В дальнейшем мы предполагаем, что все рассматриваемые точки принадлежат области 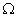 .
.
Для ориентации в строении данной координатной системы весьма полезны координатные линии. Так мы будем называть кривые, вдоль которых меняется лишь одна из координат 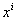 Ваа остальные остаются постоянными. Рассмотрим, например, координатную линию
Ваа остальные остаются постоянными. Рассмотрим, например, координатную линию 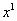 . Это значит, что
. Это значит, что 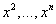 Вазакреплены на постоянных значениях, так что радиус-вектор х (7.1) остается функцией одного лишь
Вазакреплены на постоянных значениях, так что радиус-вектор х (7.1) остается функцией одного лишь 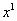 ; мы получаем кривую, отнесенную к параметру
; мы получаем кривую, отнесенную к параметру 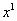 .
.
Через каждую точку М пройдет одна и только одна координатная линия 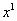 , именно, если
, именно, если 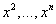 Вазакрепить на значениях, которые они имеют в точке М. Частная производная
Вазакрепить на значениях, которые они имеют в точке М. Частная производная 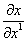 Вадает касательный вектор к координатной линии
Вадает касательный вектор к координатной линии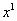 . Все сказанное справедливо и для любых координатных линий, так что через каждую точку М проходят п координатных линий с касательными векторами
. Все сказанное справедливо и для любых координатных линий, так что через каждую точку М проходят п координатных линий с касательными векторами 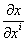 . Эти векторы мы будем обозначать кратко
. Эти векторы мы будем обозначать кратко
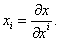 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.2)
Они, как мы знаем, всегда линейно независимы, и потому в каждой точке М могут быть приняты за векторы аффинного репера 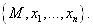 Таким образом, задание криволинейных координат в области
Таким образом, задание криволинейных координат в области 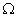 Вавлечет появление в каждой ее точке М вполне определенного аффинного репера
Вавлечет появление в каждой ее точке М вполне определенного аффинного репера 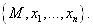 ВаЭтот аффинный репер мы будем называть локальным репером в точке М.
ВаЭтот аффинный репер мы будем называть локальным репером в точке М.
Когда в качестве частного случая криволинейных координат мы берем аффинные координаты, функция (7.1) принимает вид:
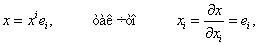 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.3)
и локальный репер в каждой точке М имеет те же векторы, что и основной репер, на котором построена данная аффинная координатная система.
Для рассмотрения локальных реперов имеются глубокие основания. Именно вспомним те простые свойства, которыми обладали аффинные координаты точек: приращения этих координат при переходе из точки 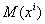 Вав точку
Вав точку 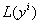 Вавыражали координаты вектора смещения
Вавыражали координаты вектора смещения 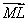 :
:
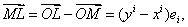
поскольку
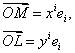
(говоря о координатах вектора, мы всегда будем иметь в виду его аффинные координаты; криволинейные координаты для векторов не имеют смысла). В этом, можно сказать, и состояла сущность аффинных координат точек.
Для криволинейных координат 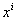 Ваэти простые свойства теряются. Однако мы находим их снова, если рассматривать криволинейные координаты в бесконечно малой окрестности данной точки М.
Ваэти простые свойства теряются. Однако мы находим их снова, если рассматривать криволинейные координаты в бесконечно малой окрестности данной точки М.
Смещаясь из точки 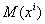 Вав бесконечно близкую точку
Вав бесконечно близкую точку 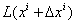 ,мы находим вектор смещения
,мы находим вектор смещения 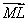 , как приращение радиуса вектора х точки М:
, как приращение радиуса вектора х точки М:
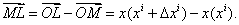
Пренебрегая бесконечно малыми высшего порядка, заменяем приращение полным дифференциалом и получаем:
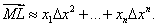 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.4)
Это значит, что вектор смещения 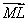 Вав локальном репере
Вав локальном репере 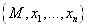 имеет координа-ты, равные приблизительно приращениям
имеет координа-ты, равные приблизительно приращениям 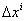 .
.
Итак, для бесконечно малых смещений из точки М приращения криволинейных координат 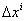 Васнова выражают координаты вектора смещения
Васнова выражают координаты вектора смещения 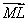 , если эти последние вычислять в локальном репере в точке М, пренебрегая бесконечно малыми высшего порядка.
, если эти последние вычислять в локальном репере в точке М, пренебрегая бесконечно малыми высшего порядка.
Таким образом, при помощи локального репера криволинейным координатам возвращаются свойства аффинных координат, правда, теперь уже лишь в бесконечно малой окрестности данной точки.
Можно сказать также, что приращения 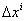 Вакриволинейных координат в бесконечно малой окрестности точки М совпадают с точностью 1-го порядка с аффинными координатами относительно локального репера, построенного в точке М.
Вакриволинейных координат в бесконечно малой окрестности точки М совпадают с точностью 1-го порядка с аффинными координатами относительно локального репера, построенного в точке М.
Естественно, что, занимаясь геометрией аффинного пространства в криволинейных координатах, мы постоянно будем сталкиваться с локальными реперами.
Выясним теперь, что происходит с локальными реперами, когда криволинейные координаты подвергаются преобразованию
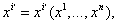 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.5)
которое предполагается однозначно обратимым и непрерывно дифференцируемым в обе стороны. Выражая, обратно,
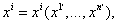 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.6)
мы можем считать в уравнении (7.1) радиус-вектор х сложной функцией от 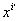 . Частная производная по
. Частная производная по 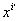 Вавыразится тогда по известной формуле:
Вавыразится тогда по известной формуле:
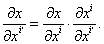
В правой части по i, конечно, происходит суммирование. Заметим, что мы будем без стеснения прилагать обычные формулы дифференцирования к выражениям, содержащим векторы, так как справедливость этих формул устанавливается тривиальным образом: достаточно свести дифференцирование векторов к дифференцированию их координат. Окончательно получаем:
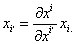 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(7.7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(7.7)
Итак, преобразование криволинейных координат влечет за собой преобразование локального репера в каждой точке М, причем векторы нового локального репера разлагаются по векторам старого с коэффициентами 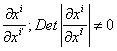 .Сравнивая с нашей прежней записью преобразования аффинного репера
.Сравнивая с нашей прежней записью преобразования аффинного репера
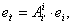
мы видим, что (7.7) представляет собой ее частный случай, когда
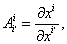 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.8)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.8)
а роль векторов 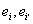 играют
играют 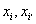 .
.
Рассмотрим теперь произвольное тензорное поле, например, 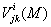 . Точка М может при этом пробегать всю область
. Точка М может при этом пробегать всю область 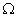 Ваили только некоторую поверхность в ней, или даже линию в зависимости от того, где тензорное поле задано.
Ваили только некоторую поверхность в ней, или даже линию в зависимости от того, где тензорное поле задано.
Координаты тензора 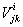 можно вычислять относительно любого аффинного репера. Однако в дальнейшем мы всегда будем считать, что аффинное пространство (по крайней мере в пределах области
можно вычислять относительно любого аффинного репера. Однако в дальнейшем мы всегда будем считать, что аффинное пространство (по крайней мере в пределах области 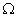 ) отнесено к каким-либо криволинейным координатам
) отнесено к каким-либо криволинейным координатам 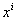 . Тогда в каждой точке М возникает локальный репер, и координаты тензора
. Тогда в каждой точке М возникает локальный репер, и координаты тензора 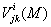 Вамы будем брать относительно именно этого репера. Эти координаты мы будем кратко называть координатами тензора
Вамы будем брать относительно именно этого репера. Эти координаты мы будем кратко называть координатами тензора 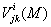 Вав данной системе криволинейных координат
Вав данной системе криволинейных координат 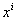 .
.
Когда в дальнейшем мы будем говорить о тензорном поле
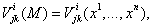 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (76.9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (76.9)
то всегда будем подразумевать сказанное выше.
Если тензорное поле задано не во всей области  , а лишь на некоторой поверхности (линии), то в уравнениях (7.9)
, а лишь на некоторой поверхности (линии), то в уравнениях (7.9)  нужно задавать, конечно, как функции параметров этой поверхности (линии). Тензорное поле может выродиться и в задание тензора
нужно задавать, конечно, как функции параметров этой поверхности (линии). Тензорное поле может выродиться и в задание тензора 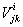 в одной только точке М.
в одной только точке М.
Вслед за преобразованием криволинейных координат происходит преобразование локального репера в каждой точке М, а значит, и преобразование координат тензора 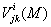 по обычному тензорному закону:
по обычному тензорному закону:
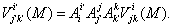 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.10)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.10)
При этом, как мы видели, матрица 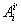 Васовпадает с матрицей
Васовпадает с матрицей 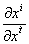 , а следовательно, обратная матрица
, а следовательно, обратная матрица 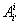 Ва- с матрицей
Ва- с матрицей 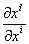 :
:
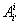 =
=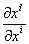 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.11)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7.11)
Следовательно, закон преобразования (7.10) принимает вид
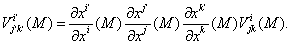 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(7.12)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(7.12)
Таким образом, переход от одних криволинейных координат к другим, влечет за собой преобразование координат тензорного поля 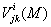 Вапо закону (7.12). При этом частные производные
Вапо закону (7.12). При этом частные производные 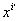 Вапо
Вапо 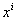 и обратно берутся в той же точке М, как и координаты тензора, что и отмечено в записи.
и обратно берутся в той же точке М, как и координаты тензора, что и отмечено в записи.
Вз8. Примеры вычислений
Пример1 (Динамика частицы)
В качестве простого приложения тензорного исчисления чуть переформулируем уравнения классической динамики материальной точки.
Второй закон Ньютона 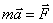 Вав компонентах записывается как
Вав компонентах записывается как
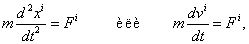 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.1)
Откуда сразу видна его ковариантность по отношению к преобразованиям из группы О (3). Если силовое поле потенциально, то
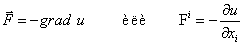 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(8.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(8.2)
Умножая обе части (8.1) на 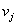 Ваи свертывая по индексам, получим
Ваи свертывая по индексам, получим
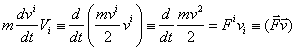
т.е.
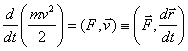 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.3)
Вводя кинетическую энергию частицу 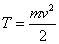 Ваи элементарную работу силы
Ваи элементарную работу силы 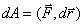 , придем к теореме живых сил.
, придем к теореме живых сил.
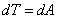 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8.4)
Инвариантной относительно ортогональных преобразований. Для потенциального стационарного поля сил и
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики