Некоторые линейные операторы
Наиболее доступными для изучения среде операторов, действующих в линейных нормированных пространствах, являются линейные операторы. Они представляют собой достаточно важный класс операторов, так как среди них можно найти операторы алгебры и анализа.
Целью дипломной работы является показать некоторые из линейных операторов, исследовать их на непрерывность и ограниченность, найти норму ограниченного оператора, а также спектр оператора и его резольвенту.
В первом и втором параграфах приведены основные сведения теории операторов: определение линейного оператора, непрерывности и ограниченности линейного оператора, его нормы. Рассмотрены некоторые примеры.
В третьем параграфе даны определения обратного оператора, спектра оператора и его резольвенты. Рассмотрены примеры.
В четвертом параграфе исследуется оператор умножения на непрерывную функцию: Ах(t) = g(t)x(t).
В пятом параграфе приведен пример оператора интегрирования Аf(t)=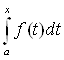 .
.
В седьмом параграфе исследуется оператор сдвига Af(x) = f(x+a).
Показана линейность, непрерывность, ограниченность, найдена норма, точки спектра и резольвента всех трех операторов.
В шестом параграфе исследуется оператор дифференцирования Дf(x)=f/(x), в пространстве дифференцируемых функции D[a, b]. Показана его линейность. Доказано, что Д не является непрерывным оператором, а также как из неограниченности оператора следует его разрывность.
Вз1. Определение линейного оператора. Примеры
Определение 1. Пусть Ex и Ey[1]
тАУ линейные пространства над полем комплексных (или действительных) чисел. Отображение А: Ex Во Ey называется линейным оператором, если для любых элементов х1 и х2 пространства Ex и любого комплексного (действительного) числа 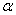 Вавыполняются следующие равенства [2]
Вавыполняются следующие равенства [2]
:
1. А(х1+х2) = Ах1 + Ах2;
2. А(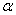 х) =
х) = 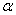 А(х);
А(х);
Примеры линейных операторов:
1) Пусть Е = Е1 тАУ линейное топологическое пространство. Оператор А задан формулой:
Ax = x для всех x  ВаЕ.
ВаЕ.
Такой оператор, переводящий каждый элемент пространства в себя является линейным и называется единичным оператором.
2) Рассмотрим D[a,b] тАУ пространство дифференцируемых функций, оператор дифференцирования Д в пространстве D[a,b] задан формулой:
Дf(x) = f/(x).
Где f(x)  ВаD[a, b], f/(x)
ВаD[a, b], f/(x)  ВаC[a, b].
ВаC[a, b].
Оператор Д определен не на всем пространстве C[a, b], а лишь на множестве функций имеющих непрерывную производную. Его линейность, очевидно, следует из свойств производной.
3) Рассмотрим пространство С[- , +
, + ] тАУ пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:
] тАУ пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:
Аf(x) = f(x+a).
Проверим линейность оператора А:
1) А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
Исходя из определения суммы функции, аксиома аддитивности выполняется.
2) A(kf(x)) = kf(x+a) = kA(f(x)).
Верна аксиома однородности.
Можно сделать вывод, что А тАУ линейный оператор.
4) Пусть 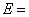
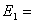
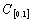 Ва(пространство непрерывных функций на отрезке [0,1], и дано отображение
Ва(пространство непрерывных функций на отрезке [0,1], и дано отображение 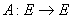 1, заданное формулой:
1, заданное формулой:
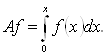
Так как интеграл с переменным верхним пределом от непрерывной функции является функцией дифференцируемой, а, следовательно, непрерывной, то 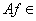
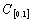 . В силу линейности определенного интеграла данное отображение является линейным оператором.
. В силу линейности определенного интеграла данное отображение является линейным оператором.
Вз2. Непрерывные линейные операторы в нормированном
пространстве. Ограниченность и норма линейного оператора
Пусть 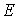 ,
, 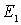 ВатАУ нормированные пространства.
ВатАУ нормированные пространства.
Определение 2 .Оператор А: Е 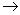 ВаЕ1 называется непрерывнымв точке
ВаЕ1 называется непрерывнымв точке 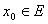 , если какова бы не была последовательность xn
, если какова бы не была последовательность xn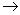 Ваx0, А(xn) сходится к А(x0). То есть, при p (xn, x0)
Ваx0, А(xn) сходится к А(x0). То есть, при p (xn, x0) 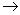 Ва0, p (А(xn), А(x0))
Ва0, p (А(xn), А(x0)) 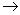 Ва0.
Ва0.
Известно и другое (равносильное) определение непрерывности линейного оператора.
Определение 3. Отображение А называется непрерывным в точке x0, если какова бы не была окрестность[3]
U точки y0 = А (x0) можно указать окрестность V точки x0 такую, что А(V) 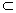 ВаU.
ВаU.
Иначе 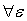 >0
>0 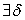 >0, что как только p (x, x0) <
>0, что как только p (x, x0) < 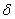 , p (f(x), f(x0)) <
, p (f(x), f(x0)) < 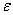 .
.
Теорема 1.
Если линейный оператор непрерывен в точке х0 = 0, то он непрерывен и в любой другой точке этого пространства.
Доказательство. Линейный оператор А непрерывен в точке х0=0 тогда и только тогда, когда 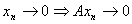 . Пусть оператор А непрерывен в точке х0=0. Возьмем последовательность точек пространства хnВох1, тогда хnтАУх1Во0, отсюда А(хnтАУх1)ВоА(0)=0, т. е. А(хnтАУх1)Во0.
. Пусть оператор А непрерывен в точке х0=0. Возьмем последовательность точек пространства хnВох1, тогда хnтАУх1Во0, отсюда А(хnтАУх1)ВоА(0)=0, т. е. А(хnтАУх1)Во0.
Так как А тАУ это линейный оператор, то А(хnтАУх1)ВоАхnтАУАх0, а тогда
Ахn-Ах0 Во 0, или АхnВоАх0.
Таким образом, из того, что линейный оператор А непрерывен в точке х0=0, следует непрерывность в любой другой точке пространства.
т. д-на.
Пример.
Пусть задано отображение F(y) = y(1) пространства С[0, 1] в R. Проверим, является ли это отображение непрерывным.
Решение.
Пусть y(x) тАУ произвольный элемент пространства С[0, 1] и yn(x) тАУ произвольная сходящаяся к нему последовательность. Это означает:
 Ваp (yn, y) =
Ваp (yn, y) = 
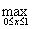 |yn(x)- y(x))| = 0.
|yn(x)- y(x))| = 0.
Рассмотрим последовательность образов: F(yn) = yn(1).
Расстояние в R определено следующим образом:
p (F(yn), F(y)) = |F(yn) - F(y))| = | yn(1) - y(1)| 
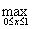 |yn(x)- y(x))|=p(yn,y),
|yn(x)- y(x))|=p(yn,y),
то есть p (F(yn), F(y)) 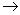 Ва0.
Ва0.
Таким образом, F непрерывно в любой точке пространства С[a, b], то есть непрерывно на всем пространстве.
С понятием непрерывности линейного оператора тесно связано понятие ограниченности.
Определение 4. Линейный оператор А: Е  ВаЕ1 называется ограниченным, если можно указать число K>0 такое, что
ВаЕ1 называется ограниченным, если можно указать число K>0 такое, что
||Аx||  ВаK||x||. ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(1)
ВаK||x||. ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(1)
Теорема 2.
Среди всех констант K, удовлетворяющих (1), имеется наименьшее.
Доказательство:
Пусть множество S тАУ множество всех констант K, удовлетворяющих (1), будучи ограниченным снизу (числом 0), имеет нижнюю грань k. Достаточно показать, что k  ВаS.
ВаS.
По свойству нижней грани в S можно указать последовательность (kn), сходящуюся к k. Так как kn ВаS, то выполняется неравенство: |А(x)|
ВаS, то выполняется неравенство: |А(x)|  Ваkn||x||, (x
Ваkn||x||, (x E). Переходя в этом неравенстве к пределу
E). Переходя в этом неравенстве к пределу
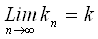
получаем |А(x)|  Ваk||x||, где (x
Ваk||x||, где (x E), (k
E), (k  ВаS).
ВаS).
т. д-на.
Определение 5. Наименьшая из этих констант K, для которых выполняется неравенство (1), называется нормой оператора А и обозначается ||A||[4]
.
||А||  ВаK, для
ВаK, для 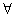 K, подходящего для (1), то есть |А(x)|
K, подходящего для (1), то есть |А(x)|  Ва||А||||x||, где
Ва||А||||x||, где
||А|| = 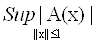
 x
x E.
E.
Между ограниченностью и непрерывностью линейного оператора существует тесная связь, а именно справедлива следующая теорема.
Теорема 3.
Для того, чтобы линейный оператор А действующий из Ex в Ey был ограничен, необходимо и достаточно, чтобы оператор А был непрерывен.
Необходимость:
Дано: А тАУ ограничен;
Доказать: А тАУ непрерывен;
Доказательство:
Используя теорему 1 достаточно доказать непрерывность А в нуле.
Дано, что ||Аx||  ВаK||x||.
ВаK||x||.
Докажем, что А непрерывен в нуле, для этого должно выполняться 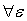 >0,
>0, 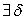 >0 что ||x||<
>0 что ||x||< 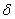
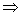 Ва||Ax|| <
Ва||Ax|| < 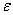 .
.
Выберем 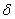 Ватак, чтобы K*||x|| <
Ватак, чтобы K*||x|| < 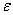 , ||x|| <
, ||x|| < 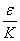 , (К>0), значит
, (К>0), значит 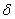 Ва=
Ва= 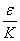 , тогда если ||x||<
, тогда если ||x||< 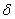 , то ||Аx||
, то ||Аx||  ВаK||x|| < K
ВаK||x|| < K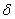 =
= 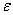
Непрерывность в нуле доказана, следовательно доказана непрерывность в 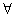 Ваточке.
Ваточке.
Достаточность:
Дано: А тАУ непрерывен;
Доказать А тАУ ограничен;
Доказательство:
Допустим, что А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1 такой, что ||A x1|| > 1|| x1||.
Числу 2 найдется вектор x2, что ||A x2|| > 2|| x2|| и т.д.
Числу n найдется вектор xn, что ||A xn|| > n|| xn||.
Теперь рассмотрим последовательность векторов yn = 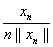 , где
, где
||yn|| = 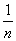 .
.
Следовательно последовательность yn Ва0 при n
Ва0 при n 
 .
.
Так как оператор А непрерывен в нуле, то Аyn Ва0, однако
Ва0, однако
||Аyn || = ||A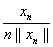 || =
|| = 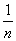 ||Axn ||
||Axn ||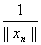 Ва> n|| xn||
Ва> n|| xn||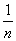
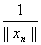 Ва= 1, получаем противоречие с Аyn
Ва= 1, получаем противоречие с Аyn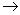 Ва0, то есть А тАУ ограничен
Ва0, то есть А тАУ ограничен
Для линейных операторов ограниченность и непрерывность оператора эквивалентны.
Примеры.
1) Покажем, что норма функционала[5]
F(y) = 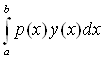 Вав C[a, b], где p(x) тАУ непрерывная на [a,b] функция, равна
Вав C[a, b], где p(x) тАУ непрерывная на [a,b] функция, равна 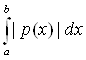 .
.
По определению 5: ||F|| = 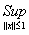 |F(x)| =
|F(x)| = 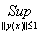 |
|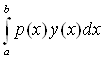 |.
|.
|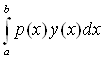 |
|  Ва|
Ва|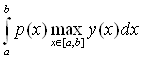 | = |
| = |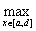 y(x)||
y(x)||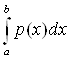 |
| 
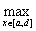 |y(x)||
|y(x)||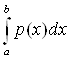 |;
|;
||F|| = 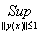 (
(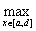 |y(x)||
|y(x)||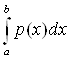 |) =
|) = 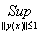 ||y(x)|||
||y(x)|||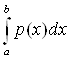 | = |
| = |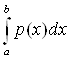 |
| 
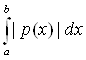 .
.
Таким образом, норма F(y) = 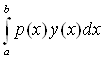 Вабудет ||F|| =
Вабудет ||F|| = 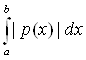 ;
;
2) Найдем норму функционала, определенного на C[0, 2], где p(x)=(x-1)
F(y) = 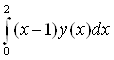 .
.
По выше доказанному ||F|| =  Ва= 1.
Ва= 1.
Вз3. Обратный оператор. Спектр оператора и резольвента
Пусть 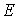 ,
, 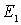 ВатАУ нормированные пространства,
ВатАУ нормированные пространства, 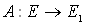 ВатАУ линейный оператор, DA- область определения оператора, а RA тАУ область значений.
ВатАУ линейный оператор, DA- область определения оператора, а RA тАУ область значений.
Определение 6. Оператор А называется обратимым, если для любого элемента у, принадлежащего RA, уравнение Ах=у имеет единственное решение.
Если оператор А обратим, то каждому элементу у, принадлежащему RA, можно поставить в соответствие единственный элемент х, принадлежащий DA и являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным оператором к оператору А и обозначается А-1.
Теорема 4.
Для того чтобы линейный оператор 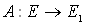 Ваимел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство:
Ваимел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство:
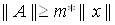 , (m>0).
, (m>0).
Доказательство:
Достаточность.
Пусть выполняется данное неравенство. Тогда равенство Ax=0 возможно лишь тогда, когда x тАУ нулевой вектор. Получим 0 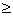 Ваm*||x||, отсюда ||x||
Ваm*||x||, отсюда ||x||  Ва0, но так как норма не может быть <0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1 существует.
Ва0, но так как норма не может быть <0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1 существует.
Докажем его ограниченность.
y=Ax.
x=A-1y, норма ||A-1y||=||x||, но ||x|| 
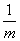 ||Ax||=
||Ax||=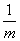 ||y||.
||y||.
Отсюда ||A-1y|| 
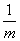 ||y||, то есть обратный оператор существует и он ограничен.
||y||, то есть обратный оператор существует и он ограничен.
Если за m возьмем наибольшую из возможных, то получим, что ||A-1||=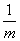 .
.
Необходимость.
Пусть от А имеется ограниченный обратный А-1 на нормированном пространстве.
Итак, ||A-1y||  ВаМ||y||.
ВаМ||y||.
Подставляем значение y и значение A-1y,получим ||x||  ВаM||Ax|| (М всегда можно считать положительным числом).
ВаM||Ax|| (М всегда можно считать положительным числом).
Отсюда ||Ax|| 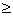
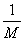 ||x||.
||x||.
Положим 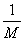 =m, получим ||Ax||
=m, получим ||Ax|| 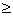 Ваm||x||.
Ваm||x||.
т. д-на.
В теории операторов важную роль играет понятие спектра оператора. Рассмотрим это понятие сначала для конечномерного пространства.
Определение 7. Пусть А тАУ линейный оператор в n-мерном пространстве Еn. Число λ называется собственным значением оператора А, если уравнение Ах=λх имеет ненулевые решения. Совокупность всех собственных значений называется спектромоператора А, а все остальные значения λ тАУ регулярными. Иначе говоря, λ есть регулярная точка, если оператор 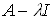 , где I тАУ единичный оператор, обратим, При этом оператор (А тАУ λI)-1, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности:
, где I тАУ единичный оператор, обратим, При этом оператор (А тАУ λI)-1, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности:
1) уравнение Ах=λх имеет ненулевое решение, то есть λ является собственным значением для оператора А; оператор (А тАУ λI)-1 при этом не существует;
2) существует ограниченный оператор (А тАУ λI)-1, то есть λ есть регулярная точка.
В бесконечном пространстве имеется еще и третья возможность, а именно:
3) оператор (А тАУ λI)-1 существует, то есть уравнение Ах=λх имеет лишь нулевое решение, но этот оператор не ограничен.
Введем следующую терминологию. Число λ мы назовем регулярным для оператора А, действующего в линейном нормированном пространстве Е, если оператор (А тАУ λI)-1, называемый резольвентой оператора А, определен на всем пространстве Е и непрерывен. Совокупность всех остальных значений λ называется спектром оператора А. Спектру принадлежат все собственные значения оператора А, так как, если (А тАУ λI)х=0 при некотором х≠0, то оператор (А тАУ λI)-1 не существует. Их совокупность называется точечным спектром. Остальная часть спектра, то есть совокупность тех λ, для которых (А тАУ λI)-1 существует, но не непрерывен, называется непрерывным спектром. Итак, каждое значение λ является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра тАУ существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
Определение 8. Оператор 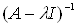 , где
, где 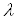 ВатАУ регулярная точка оператора А, называется резольвентой[6]
ВатАУ регулярная точка оператора А, называется резольвентой[6]
оператора А и обозначается 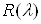 Ва(или
Ва(или 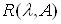 ).
).
Теорема 5. Пусть 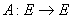 ВатАУ линейный непрерывный оператор,
ВатАУ линейный непрерывный оператор, 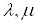 Ваего регулярные числа. Тогда
Ваего регулярные числа. Тогда 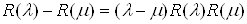 .
.
Доказательство. Умножим обе части равенства на 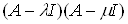 :
: 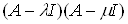 (
(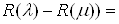
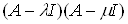
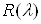
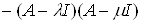
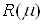 =
=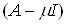
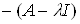 =
=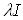
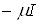 . С другой стороныВа получим
. С другой стороныВа получим 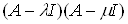
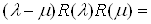
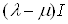 . Так как числа
. Так как числа 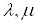 ВатАУ регулярные для оператора А, то оператор
ВатАУ регулярные для оператора А, то оператор 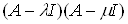 Ваимеет обратный. Значит, из равенства
Ваимеет обратный. Значит, из равенства 
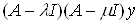 Васледует, что
Васледует, что 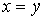 . Значит, утверждение теоремы верно.
. Значит, утверждение теоремы верно.
т. д-на.
Примеры.
1) Рассмотрим в пространстве C[0,1] оператор умножения на независимую переменную t: Ax = tx(t).
Уравнение Аx= x принимает в этом случае вид:
x принимает в этом случае вид:
tx(t) -  x(t) = y(t),
x(t) = y(t),
решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая.
Если  Валежит вне отрезка [0, 1], то уравнение Аx=
Валежит вне отрезка [0, 1], то уравнение Аx= x имеет при любом y(t) единственное непрерывное решение:
x имеет при любом y(t) единственное непрерывное решение:
x(t) = 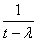 y(t),
y(t),
откуда следует, что все такие значения параметра  Ваявляются регулярными, и резольвента есть оператор умножения на
Ваявляются регулярными, и резольвента есть оператор умножения на 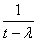 :
:
R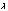 (y) =
(y) = 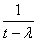 y(t).
y(t).
Все значения параметра, принадлежащие отрезку[0, 1], являются точками спектра. В самом деле, пусть  0
0 Ва[0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке
Ва[0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке  0, y(
0, y( 0) = a
0) = a 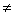 Ва0. Для такой функции равенство (t -
Ва0. Для такой функции равенство (t -  0)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t =
0)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t =  0 левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при
0 левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при  Ва=
Ва=  0 уравнение Аx=
0 уравнение Аx= x не имеет решения для произвольной правой части, что и доказывает принадлежность
x не имеет решения для произвольной правой части, что и доказывает принадлежность  0 спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t -
0 спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t -  )x(t) = 0,
)x(t) = 0, 
 Ва[0, 1], при любом t, отличном от
Ва[0, 1], при любом t, отличном от  , а следовательно, в силу непрерывности и при t =
, а следовательно, в силу непрерывности и при t =  , обращается в нуль, т.е. тождественно равно нулю.
, обращается в нуль, т.е. тождественно равно нулю.
2) Пусть оператор А действующий из Е 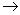 ВаЕ, задается матрицей А=
ВаЕ, задается матрицей А= .
.
Аx = 
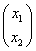 Ва=
Ва= 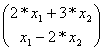 .
.
Введем обозначения:
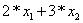 Ва= y1
Ва= y1
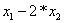 Ва= y2
Ва= y2
x1, x2, y1, y2 ВаE;
ВаE;
A -  *I =
*I = 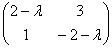 , найдем определитель A -
, найдем определитель A -  *I:
*I:
D(A -  *I) =
*I) = 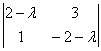 Ва= (2-
Ва= (2- )*(-2-
)*(-2- ) тАУ 3 =
) тАУ 3 =  2 тАУ 7;
2 тАУ 7;
Если определитель отличен от нуля, то есть если  Ване есть корень уравнения
Ване есть корень уравнения  2 тАУ 7 = 0, следовательно, все такие значения параметра
2 тАУ 7 = 0, следовательно, все такие значения параметра  Варегулярные.
Варегулярные.
Корни уравнения  2 тАУ 7 = 0 образуют спектр:
2 тАУ 7 = 0 образуют спектр:
 1 =
1 = 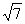 ;
;  2 = -
2 = -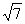 ;
;
 1,
1,  2 тАУ собственные значения.
2 тАУ собственные значения.
Найдем собственные векторы для собственных значений  :
:
при  Ва=
Ва= 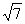 Ваполучаем:
Ваполучаем:
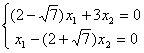
откуда x1 = (2+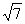 )x2; 1-й собственный вектор: ((2+
)x2; 1-й собственный вектор: ((2+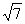 )x, x);
)x, x);
при  Ва= -
Ва= -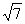 получаем:
получаем:
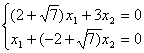
откуда x1 = (2 - 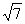 )x2 ; 2-й собственный вектор: ((2 -
)x2 ; 2-й собственный вектор: ((2 - 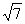 )x, x);
)x, x);
Вз4. Оператор умножения на непрерывную функцию
Рассмотрим пространство 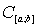 Ванепрерывных на отрезке
Ванепрерывных на отрезке 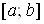 Вафункций, и оператор А, заданный формулой:
Вафункций, и оператор А, заданный формулой:
Ах(t) = g(t) x(t).
g(t) - функция, непрерывная на [a, b]; a,b R.
R.
Проверим является ли оператора А линейным, то есть, по определению 1, должны выполняться аксиомы аддитивности и однородности.
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = (g(t)+f(t))x(t) = g(t)x(t)+f(t)x(t) = A(f) + A(g).
2) Аксиома однородности: A(k*f) = k*A(f).
A(k*f) = A(k*x(t)) = k*g(t)x(t) = kA(x(t)) = k*A(f).
По средствам арифметических операции над функциями, аксиомы аддитивность и однородность выполняются. Оператор А является линейным по определению.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn(x), f0(x)) 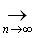 Ва0ВаВаВа
Ва0ВаВаВа 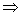 ВаВаВаВаp (A fn(x), Af0(x))
ВаВаВаВаp (A fn(x), Af0(x)) 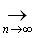 0.
0.
Оператор А, действует в пространстве C[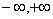 ], в котором расстояние между функциями определяется следующим образом:
], в котором расстояние между функциями определяется следующим образом:
p (fn(x), f0(x)) = 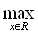 | fn(x) - f0(x)|.
| fn(x) - f0(x)|.
Решение:
p (A xn(t), Ax0(t)) = 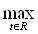 |Axn(t) - Ax0(t)| =
|Axn(t) - Ax0(t)| = 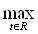 |xn(t)g(t) - x0(t)g(t)|
|xn(t)g(t) - x0(t)g(t)| 
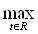 |g(t)|
|g(t)| 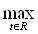 |xn(t) - x0(t)| =
|xn(t) - x0(t)| = 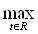 |g(t)|p (xn(t), x0(t))
|g(t)|p (xn(t), x0(t)) 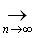 Ва0.
Ва0.
Итак, p (A xn(t), Ax0(t)) 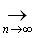 Ва0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен.
Ва0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен.
4) Оператор А ограниченный, следовательно у него можно найти норму.
По определению 5: ||A||=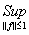 |A(f)|.
|A(f)|.
Решение.
||A||=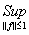 |A(f)|=
|A(f)|=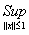 |g(t)x(t)|.
|g(t)x(t)|.
|g(t)x(t)|  Ва|g(t)
Ва|g(t) 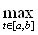 x(t)| = |g(t)| |
x(t)| = |g(t)| |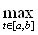 x(t)|
x(t)| 
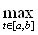 |x(t)| |g(t)|.
|x(t)| |g(t)|.
||A||=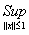
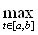 |x(t)| |g(t)| =
|x(t)| |g(t)| = 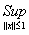 Ва||x(t)|| |g(t)|
Ва||x(t)|| |g(t)|  Ва|g(t)|.
Ва|g(t)|.
Норма оператора А: ||A|| = |g(t)|.
5) Обратимость оператора А, его спектр и резольвента.
Возьмем произвольное число 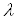 Ваи составим оператор
Ваи составим оператор 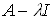 :
:
(А-lI) x(t) = (g(t) тАУl ) х(t).
Чтобы найти обратный оператор, нужно решить уравнениеВа 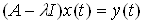 Ваотносительно функции
Ваотносительно функции 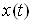 . Это возможно, если
. Это возможно, если 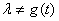 Вадля любого
Вадля любого 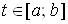 :
:
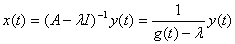 .
.
Если число 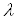 Ване является значение функции g(t), то знаменатель не обращается в 0, и функция
Ване является значение функции g(t), то знаменатель не обращается в 0, и функция 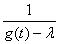 Ванепрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке
Ванепрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке 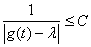 . Отсюда следует, что оператор
. Отсюда следует, что оператор 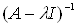 Ваявляется ограниченным.
Ваявляется ограниченным.
Если же 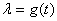 , то оператор
, то оператор 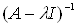 Ване существует. Следовательно, спектр оператора состоит из всех l = g(t).
Ване существует. Следовательно, спектр оператора состоит из всех l = g(t).
Резольвента оператора имеет вид 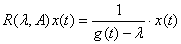 .
.
Отметим, что точки спектра 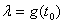 ,
, 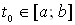 , не являются собственными числами. Не существует такой непрерывной функции
, не являются собственными числами. Не существует такой непрерывной функции 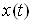 , для которой
, для которой 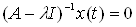 , или
, или 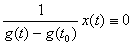 . Поэтому весь спектр данного оператора является непрерывным.
. Поэтому весь спектр данного оператора является непрерывным.
Вывод:
Оператор A, заданный формулой: Ах(t) = g(t)x(t), где g(t) - функция, непрерывная на [a, b], a,b R:
R:
1. Валинейный;
2. непрерывный;
3. ограниченный, с нормой ||A|| = |g(t)|;
4. обратим при 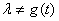 , для любого
, для любого 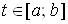 ;
;
5. спектр оператора состоит из всех l = g(t); спектр данного оператора является непрерывным;
6. резольвента имеет вид 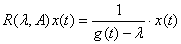 .
.
Вз5.Оператор интегрирования
Рассмотрим оператор интегрирования, действующий в пространстве непрерывных функций - C[a,b], определенных на отрезке [a,b], заданный следующим образом:
Аf(t) = 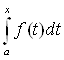 .
.
f(t) тАУ функция, непрерывная на [a, b],t  Ва[a,x]; x
Ва[a,x]; x  Ва[a,b]; a,b
Ва[a,b]; a,b R;
R;
Поскольку 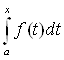 Ва- интеграл с переменным верхним пределом, есть функция от верхнего предела тАУ F(x), a
Ва- интеграл с переменным верхним пределом, есть функция от верхнего предела тАУ F(x), a  Ваx
Ваx  Ваb; Следовательно можно утверждать, что А тАУ оператор.
Ваb; Следовательно можно утверждать, что А тАУ оператор.
Проверим оператор A на линейность. По определению 1:
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = 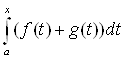 Ва=
Ва= 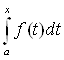 Ва+
Ва+ 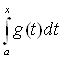 Ва= A(f) + A(g).
Ва= A(f) + A(g).
2) Аксиома однородности: A(kf) = kA(f).
A(kf) = 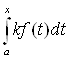 Ва= k*
Ва= k*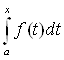 Ва= kA(f).
Ва= kA(f).
Исходя из свойств интеграла:
1. интеграл от суммы, есть сумма интегралов;
2. вынесение const за знак интеграла.
Можно сделать вывод: оператор А является линейным.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn(t), f0(t)) 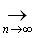 Ва0ВаВаВа
Ва0ВаВаВа 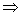 ВаВаВаВаp (A fn(t), Af0(t))
ВаВаВаВаp (A fn(t), Af0(t)) 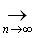 0.
0.
Оператор А, действует в пространстве C[a,b], в котором расстояние между функциями определяется следующим образом:
p (fn(t), f0(t)) = 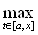 | fn(t) - f0(t)|.
| fn(t) - f0(t)|.
Решение:
p (A fn(t), Af0(t)) = 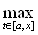 |
|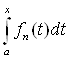 Ва-
Ва- 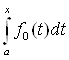 |.
|.
|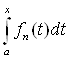 Ва-
Ва- 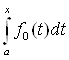 | = |
| = |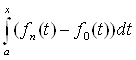 |
| 
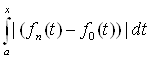

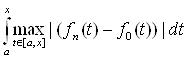 Ва= p (fn(t), f0(t))
Ва= p (fn(t), f0(t)) 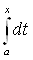 Ва= p (fn(t), f0(t)) (x-a)
Ва= p (fn(t), f0(t)) (x-a) 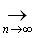 Ва0
Ва0
a x
x b.
b.
Таким образом p (A fn(t), Af0(t)) 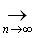 Ва0. следовательно по определению 2 оператор А непрерывен.
Ва0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
|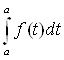 |
|  Ва|
Ва|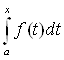 |
|  Ва|
Ва|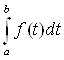 |
|
|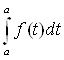 | = 0; |
| = 0; |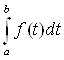 | = |b-a|.
| = |b-a|.
0  Ва|
Ва|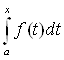 |
|  Ва|b-a|.
Ва|b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||=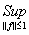 |A(f)|):
|A(f)|):
||A|| = 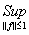 |A(f)| =
|A(f)| = 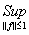 Ва|
Ва|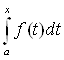 |
| 
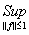
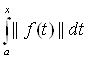

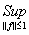
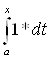 Ва= (x-a);
Ва= (x-a);
a  Ваx
Ваx  Ваb;
Ваb;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f  ВаC[0,b] / f(0) = 0} с нормой ||f|| =
ВаC[0,b] / f(0) = 0} с нормой ||f|| = 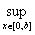 |f(x)|.
|f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 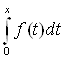
x  Ва[0,b], t
Ва[0,b], t  Ва[0,x];
Ва[0,x];
Найдем оператор обратный к (A -  *I),
*I), 
 ВаR;
ВаR;
(A -  *I)*f = g
*I)*f = g
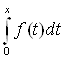 Ва-
Ва-  *f(x) = g(x)ВаВаВаВаВаВаВаВаВа (1)
*f(x) = g(x)ВаВаВаВаВаВаВаВаВа (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f -  *f/ = g/ВаВаВаВаВаВаВаВаВаВа (2)
*f/ = g/ВаВаВаВаВаВаВаВаВаВа (2)
Это уравнение (2) тАУ дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
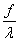 Ва- f/ =
Ва- f/ = 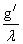
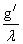 Ва-
Ва- 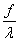 Ва+ f/ = 0ВаВаВаВаВаВаВаВаВаВа (3)
Ва+ f/ = 0ВаВаВаВаВаВаВаВаВаВа (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
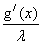 Ва-
Ва- 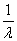 *U*V + U/ *V + U*V/ Ва= 0
*U*V + U/ *V + U*V/ Ва= 0
U/ *V + U*V/ - 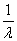 *U*V = -
*U*V = - 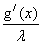
U/ *V + U*(V/ - 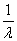 *V) = -
*V) = - 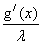 ВаВаВаВаВаВаВаВаВа(4)
ВаВаВаВаВаВаВаВаВа(4)
Решаем однородное линейное уравнение:
V/ - 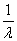 *V = 0
*V = 0
V/ = 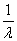 *V
*V
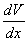 Ва=
Ва= 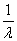 *V
*V
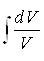 Ва=
Ва= 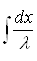
LnV = 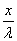 Ва+ c
Ва+ c
V = 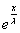 *
*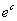 , пусть
, пусть 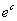 Ва= с1
Ва= с1
V = с1*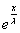
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/ - 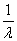 *V = 0.
*V = 0.
Получим уравнение:
U/ * с1*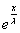 Ва= -
Ва= - 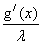
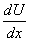 Ва= -
Ва= -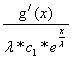
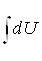 Ва= -
Ва= - 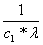 *
*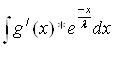
U = -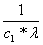 *
*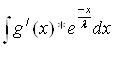
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1*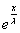 *(-
*(-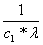 )*
)*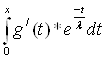
найдем интеграл Y = 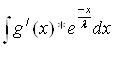 , интегрируем по частям:
, интегрируем по частям:
dz = g/(x)dx;
z = 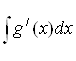 Ва= g(x);
Ва= g(x);
j = 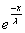 ;
;
dj = - 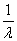 *
*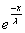 dx;
dx;
Y = g(x)* 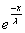 Ва+
Ва+ 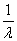 *
*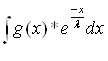
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = -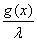 Ва-
Ва- 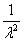 *
*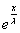 *
*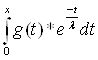 ;
;
Получим оператор В:
Bg = -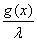 Ва-
Ва- 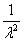 *
*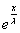 *
*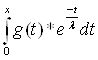 ;
;
x  Ва[0,b], t
Ва[0,b], t  Ва[0,x], g(x)
Ва[0,x], g(x)  ВаS,
ВаS,  Ва- произвольное число.
Ва- произвольное число.
Оператор В не существует, если  Ва= 0;
Ва= 0;
Рассмотрим ограниченность оператора В для всех 
 ВаR,
ВаR, 
 Ва0;
Ва0;
||Bg|| = ||f(x)|| =  |f(x)| =
|f(x)| =  |-
|-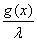 Ва-
Ва- 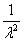 *
*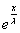 *
*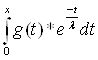 |
| 
 (|
(|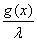 | + |
| + |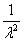 *
*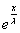 *
*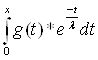 |)
|) 
 |
|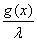 | +
| +  |
|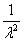 *
*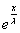 *
*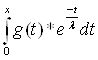 |
| 
 |
|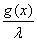 | +
| +  |
|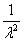 *
*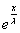 |*
|* |g(x)*
|g(x)* 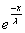 |*|x|
|*|x| 
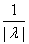 *
* |g(x)| +
|g(x)| + 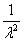

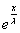 *
* |g(x)|*
|g(x)|*  (|
(|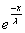 |*|x|)
|*|x|) 
 |g(x)|*(
|g(x)|*( 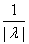 Ва+
Ва+ 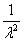 *
*
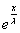 *
*
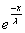 *b);
*b);
При  Ва> 0
Ва> 0

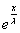 Ва=
Ва= 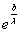 ;
;

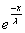 Ва= 1;
Ва= 1;
При  Ва< 0
Ва< 0

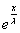 Ва=1;
Ва=1;

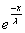 Ва=
Ва= 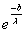 ;
;
Эти оба случая можно записать в общем виде: 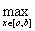 {1,
{1, 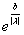 }, тогда
}, тогда
 |g(x)|*(
|g(x)|*( 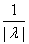 Ва+
Ва+ 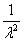 *
* Вместе с этим смотрят:
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики