Нестандартные методы решения задач по математике
1. Метод функциональной подстановки
2. Метод тригонометрической подстановки
3. Методы, основанные на применении численных неравенств
4. Методы, основанные на монотонности функций
5. Методы решения функциональных уравнений
6. Методы, основанные на применении векторов
7. Комбинированные методы
8. Методы, основанные на использовании ограниченности функций
9. Методы решения симметрических систем уравнений
10. Методы решения уравнений, содержащих целые или дробные части числа
Заключение
Литература
Введение
В настоящее время на занятиях по математике в математических классах общеобразовательных школ, гимназий и лицеев все большее внимание уделяется изучению нестандартных методов решения уравнений и неравенств из различных разделов математики (алгебра, тригонометрия и геометрия). В известной степени это вызвано тем, что в последние годы имеет место устойчивая тенденция к усложнению заданий, предлагаемых на вступительных экзаменах по математике в ведущих высших учебных заведениях Беларуси и Российской Федерации.
В данной работе предлагаются нестандартные методы решения задач по математике, которые имеют довольно-таки широкое распространение. Многие из приведенных здесь задач предлагались совсем недавно на вступительных экзаменах по письменной математике в Белгосуниверситете.
1. Метод функциональной подстановки
Метод функциональной подстановки является, пожалуй, самым распространенным методом решения сложных задач школьной математики. Суть метода состоит в введении новой переменной 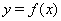 , применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
, применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
Основная трудность решения задач методом функциональной подстановки заключается в том, что зачастую трудно угадать вид самой подстановки и вид уравнений (или неравенств), где эту подстановку можно использовать. В настоящем разделе предлагаются наиболее распространенные уравнения и неравенства, которые эффективно решаются методом функциональной подстановки.
Задачи и решения
Пример 1Решить уравнение
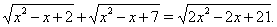
Решение. Введем новую переменную 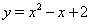 , тогда из Ошибка! получаем уравнение
, тогда из Ошибка! получаем уравнение 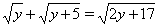 . Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение
. Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение 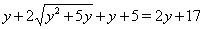 . Отсюда вытекает
. Отсюда вытекает 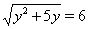 ,
, 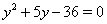 Ваи
Ваи 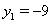 ,
, 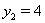 .
.
Рассмотрим два уравнения
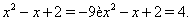
Первое уравнение корней не имеет, а из второго получаем 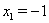 Ваи
Ваи 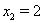 . Подстановкой в Ошибка! убеждаемся в том, что найденные значения переменной
. Подстановкой в Ошибка! убеждаемся в том, что найденные значения переменной 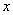 Ваявляются корнями исходного уравнения.
Ваявляются корнями исходного уравнения.
Ответ: 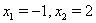 .
.
Пример 2Решить уравнение
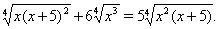
Решение. Нетрудно видеть, что 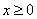 Ваи
Ваи 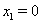 Ваявляется корнем уравнения.
Ваявляется корнем уравнения.
Пусть теперь 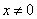 , тогда обе части уравнения Ошибка! разделим на
, тогда обе части уравнения Ошибка! разделим на 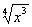 Ваи получим уравнение
Ваи получим уравнение
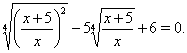
Если обозначить 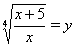 , то уравнение Ошибка! принимает вид квадратного уравнения
, то уравнение Ошибка! принимает вид квадратного уравнения  , корнями которого являются
, корнями которого являются 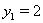 Ваи
Ваи 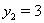 .
.
Рассмотрим уравнения 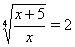 Ваи
Ваи 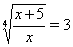 , откуда следует, что
, откуда следует, что 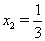 Ваи
Ваи 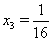 . Так как
. Так как 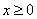 , то наиденные значения
, то наиденные значения 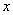 Ваявляются корнями уравнения.
Ваявляются корнями уравнения.
Ответ: 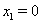 ,
, 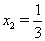 ,
, 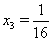 .
.
Пример 3Решить уравнение
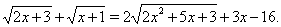
Решение. Перепишем уравнение в виде
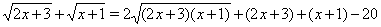
Положим, что 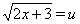 Ваи
Ваи 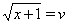 , тогда из Ошибка! получим уравнение
, тогда из Ошибка! получим уравнение  , из которого следует
, из которого следует 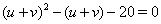 Ваи
Ваи 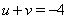 ,
, 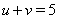 . Так как
. Так как 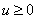 Ваи
Ваи 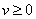 , то
, то 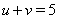 Ваи при этом
Ваи при этом 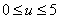 .
.
Поскольку 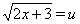 Ваи
Ваи 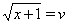 , то
, то 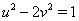 . Отсюда получаем систему уравнений
. Отсюда получаем систему уравнений
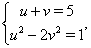
где 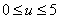 . Решением системы уравнений Ошибка! относительно
. Решением системы уравнений Ошибка! относительно 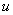 Ваявляется
Ваявляется 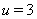 . Так как при этом
. Так как при этом 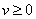 Ваи
Ваи 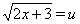 , то
, то 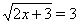 Ваи
Ваи 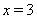 .
.
Ответ: 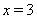 .
.
Пример 4Решить уравнение
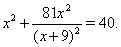
Решение. Для преобразования левой части уравнения Ошибка! воспользуемся очевидным равенством 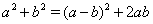 . Тогда из уравнения Ошибка! имеем
. Тогда из уравнения Ошибка! имеем
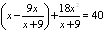
и
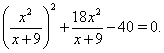
Если затем положить 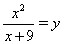 , то получим уравнение
, то получим уравнение 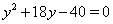 , корни которого равны
, корни которого равны 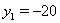 Ваи
Ваи 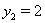 .
.
Таким образом, необходимо рассмотреть два уравнения 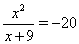 Ваи
Ваи 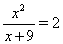 , т.е.
, т.е. 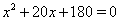 Ваи
Ваи 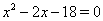 , где
, где  . Первое уравнение корней не имеет, а из второго получаем
. Первое уравнение корней не имеет, а из второго получаем 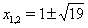 .
.
Ответ: 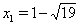 ,
, 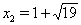 .
.
Пример 5Решить уравнение
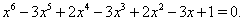
Решение. Первоначально убедимся, что 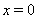 Ване является корнем уравнения Ошибка!. Так как
Ване является корнем уравнения Ошибка!. Так как 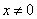 , то разделим обе части уравнения Ошибка! на
, то разделим обе части уравнения Ошибка! на 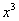 . Тогда получим
. Тогда получим
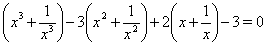 (1)
(1)
Пусть 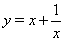 , тогда
, тогда
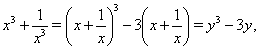
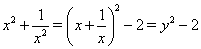
и из уравнения (1) следует 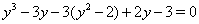 Ваили
Ваили 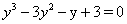 . Последнее уравнение представим в виде
. Последнее уравнение представим в виде 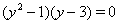 . Отсюда следует, что
. Отсюда следует, что 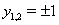 Ваи
Ваи 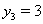 .
.
Далее, рассмотрим три уравнения 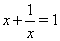 ,
, 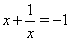 Ваи
Ваи 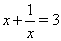 . Первые два уравнения корней не имеют, а корнями третьего уравнения
. Первые два уравнения корней не имеют, а корнями третьего уравнения 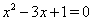 Ваявляются
Ваявляются 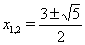
Ответ: 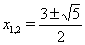
Пример 6Решить неравенство
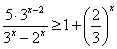 (2)
(2)
Решение. Разделим числитель и знаменатель дроби в левой части неравенства (2) на 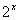 Ваи обозначим
Ваи обозначим 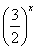 Вачерез
Вачерез 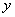 . Тогда неравенство (2) можно переписать как
. Тогда неравенство (2) можно переписать как
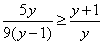
и
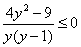 (3)
(3)
Решая неравенство (3) с учетом того, что 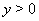 , получаем
, получаем 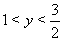 . Поскольку
. Поскольку 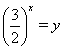 , то
, то 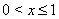 .
.
Ответ: 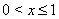 .
.
Пример 7
Решить уравнение
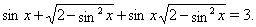 (4)
(4)
Решение. Выполним замену переменных, пусть 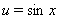 Ваи
Ваи 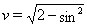 . Так как
. Так как 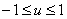 Ваи
Ваи 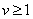 , тo
, тo 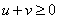 . Кроме того, имеем
. Кроме того, имеем 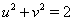 .
.
В таком случае из уравнения (4) получаем систему уравнений
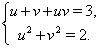 (5)
(5)
Пусть теперь 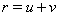 Ваи
Ваи 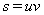 , тогда из системы уравнений (5) следует
, тогда из системы уравнений (5) следует 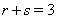 Ваи
Ваи 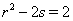 . Отсюда с учетом того, что
. Отсюда с учетом того, что 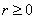 , получаем
, получаем 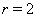 Ваи
Ваи 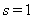 . Следовательно, имеет место
. Следовательно, имеет место 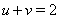 ,
, 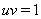 Ваи
Ваи 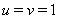 .
.
Поскольку 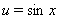 Ваи
Ваи 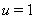 , то
, то 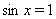 Ваи
Ваи 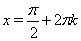 , где
, где 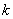 Ва--- целое число.
Ва--- целое число.
Ответ: 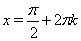 , где
, где 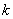 Ва--- целое число.
Ва--- целое число.
2. Метод тригонометрической подстановкиК числу, нестандартных методов решения алгебраических уравнений относится метод, основанный на применении тригонометрической подстановки. Использование такого метода целесообразно в том случае, когда искомые уравнения напоминают известные тригонометрические формулы. Это относится преимущественно к уравнениям (системам уравнений), решение которых обычными приемами весьма затруднительно, и которые после введения тригонометрических подстановок сводятся к несложным тригонометрическим уравнениям. Суть тригонометрической подстановки состоит в замене неизвестной переменной 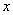 Ватригонометрической функцией, например
Ватригонометрической функцией, например 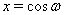 Ваили
Ваили 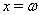 , а также в замене
, а также в замене 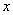 Ванекоторой функцией от
Ванекоторой функцией от 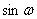 ,
, 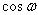 Ваили
Ваили 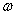 .
.
Полученные корни тригонометрических уравнений позволяют находить корни исходных уравнений как в тригонометрической, так и в алгебраической форме. Следует особо отметить, что тригонометрические уравнения имеют, как правило, бесконечное число корней, а исходные уравнения --- конечное их число.
Задачи и решения
Пример 8Решить уравнение
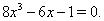 (6)
(6)
Решение. Поскольку 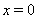 Ване является корнем уравнения (6), то разделим обе его части на
Ване является корнем уравнения (6), то разделим обе его части на 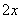 . Тогда
. Тогда
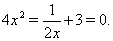 (7)
(7)
Если 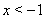 Ваили
Ваили 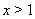 , то левая часть уравнения (7) будет больше
, то левая часть уравнения (7) будет больше 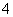 , а правая его часть --- меньше
, а правая его часть --- меньше 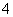 . Следовательно, корни уравнения (6) находятся на отрезке
. Следовательно, корни уравнения (6) находятся на отрезке 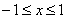 .
.
Пусть 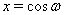 , где
, где 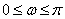 . Тогда уравнение (6) принимает вид тригонометрического уравнения
. Тогда уравнение (6) принимает вид тригонометрического уравнения
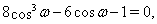
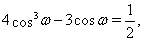
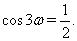
Решением уравнения 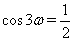 Ваявляются
Ваявляются 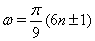 , где
, где 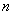 Ва--- целое число. Однако
Ва--- целое число. Однако 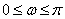 , поэтому
, поэтому 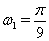 ,
, 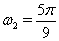 Ваи
Ваи 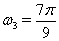 . Так как
. Так как 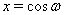 , то
, то 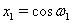 ,
, 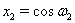 Ваи
Ваи 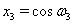 .
.
Ответ: 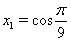 ,
, 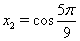 Ваи
Ваи 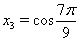 .
.
Пример 9Решить уравнение
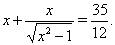 (8)
(8)
Решение. Нетрудно видеть, что
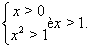
Выполним замену 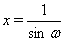 , где
, где 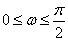 . В таком случае левая часть уравнения (8) принимает вид
. В таком случае левая часть уравнения (8) принимает вид
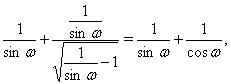
а из уравнения (8) следует тригонометрическое уравнение вида
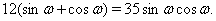 (9)
(9)
Сделаем еще одну замену переменных, пусть 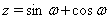 , тогда
, тогда 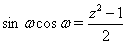 Ваи из (9) получаем квадратное уравнение относительно переменной
Ваи из (9) получаем квадратное уравнение относительно переменной 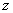 , т.е.
, т.е. 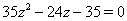 , решением которого являются
, решением которого являются 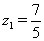 Ваи
Ваи 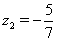 . Так как
. Так как 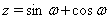 Ваи
Ваи 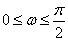 , то
, то 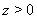 Ваи
Ваи 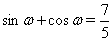 . С учетом того, что
. С учетом того, что 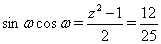 , получаем систему тригонометрических уравнений
, получаем систему тригонометрических уравнений
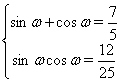 (10)
(10)
Из уравнений системы (10) составим квадратное уравнение относительно 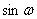 Вавида
Вавида 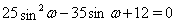 Ваи получаем
Ваи получаем 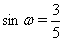 Ваи
Ваи 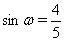 . Так как
. Так как 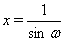 , то
, то 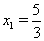 Ваи
Ваи 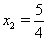
Ответ: 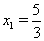 ,
, 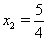 .
.
Пример 10
Решить систему уравнений
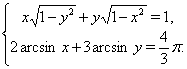 (11)
(11)
Решение. Поскольку 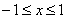 Ваи
Ваи 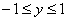 , то положим
, то положим 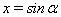 Ваи
Ваи 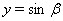 , тогда
, тогда 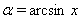 Ваи
Ваи 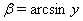 . Тогда
. Тогда 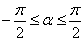 Ваи
Ваи 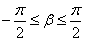 . В таком случае
. В таком случае 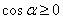 ,
, 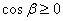 Ваи система уравнений (11) принимает вид
Ваи система уравнений (11) принимает вид
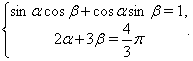 (12)
(12)
Из первого уравнения системы (12) получаем 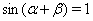 . Поскольку
. Поскольку 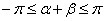 , то
, то 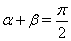 , Следовательно, получаем систему
, Следовательно, получаем систему
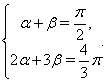
Отсюда следует 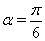 Ваи
Ваи 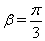 . Так как
. Так как 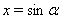 Ваи
Ваи 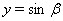 , то
, то 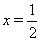 Ваи
Ваи 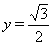 .
.
Ответ: 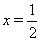 ,
, 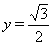 .
.
3. Методы, основанные на применении численных неравенствНестандартными методами в математике являются также методы, в основу которых положено использование известных в математике численных неравенств (Коши, Бернулли и Коши--Буняковского), изучению которых в общеобразовательной школе не уделяется или почти не уделяется никакого внимания. Однако многие математические задачи (особенно задачи повышенной сложности) эффективно решаются именно такими методами. В этой связи незнание последних может существенно ограничить круг успешно решаемых задач.
Первоначально приведем формулировки неравенства Коши, неравенства Бернулли и неравенства Коши--Буняковского, а затем проиллюстрируем их применение на примерах, взятых из программы вступительных экзаменов по письменной математике в Белгосуниверситете.
Неравенство Коши
Пусть 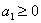 ,
, 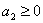 , ..,
, .., 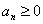 , тогда
, тогда
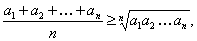 (13)
(13)
где 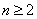 . Причем неравенство превращается в равенство тогда и только тогда, когда
. Причем неравенство превращается в равенство тогда и только тогда, когда 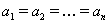 . В частности, если в (13) положить
. В частности, если в (13) положить 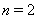 , то
, то
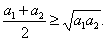 (14)
(14)
Это неравенство чаще всего встречается при решении школьных задач по математике. Если в (14) положить 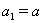 Ваи
Ваи 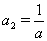 , где
, где 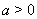 , то
, то
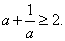 (15)
(15)
Здесь неравенство равносильно равенству лишь при 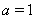 .
.
Следует отметить, что имеется аналог неравенства (15) для отрицательных значений  , а именно, если
, а именно, если 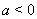 , то
, то
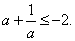 (16)
(16)
Данное неравенство превращается в равенство при 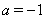 .
.
Неравенство Бернулли
Наиболее распространенным является классическое неравенство Бернулли, которое формулируется в следующей форме: если 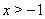 , то для любого натурального
, то для любого натурального 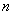 Ваимеет место
Ваимеет место
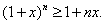 (17)
(17)
Причем равенство в (17) достигается при 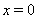 Ваили
Ваили 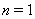 .
.
Наряду с (17) существует обобщенное неравенство Бернулли, которое содержит в себе два неравенства:
Ваесли 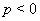 Ваили
Ваили 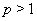 , то
, то
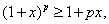 (18)
(18)
если 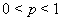 , то
, то
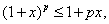 (19)
(19)
где 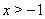 .
.
Следует отметить, что равенства в (18) и (19) имеют место только при 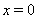 . Верно также и обратное утверждение.
. Верно также и обратное утверждение.
Неравенство Коши--Буняковского
Для произвольных 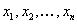 Ваи
Ваи 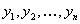 Ваимеет место
Ваимеет место
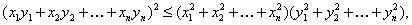 (20)
(20)
где 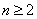 .
.
Причем равенство в (20) достигается в том и только в том случае, когда числа 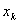 . и
. и 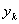 Вапропорциональны, т.е. существует константа
Вапропорциональны, т.е. существует константа 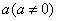 Ватакая, что для всех
Ватакая, что для всех 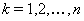 Вавыполняется равенство
Вавыполняется равенство 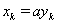 .
.
На основе использования неравенства Коши--Буняковского (20) можно доказать неравенство
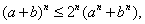 (21)
(21)
которое справедливо для произвольных 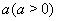 ,
, 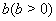 Ваи натурального числа
Ваи натурального числа 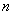 .
.
Задачи и решения
Пример 11Доказать неравенство
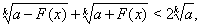 (22)
(22)
где 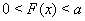 .
.
Доказательство. Преобразуем левую часть неравенства (22) с использованием неравенства (19), т.е.
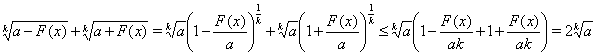
Так как по условию 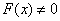 , то равенства в неравенстве Бернулли (19) не будет, поэтому доказано строгое неравенство (22).
, то равенства в неравенстве Бернулли (19) не будет, поэтому доказано строгое неравенство (22).
Пример 12Доказать, что если 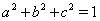 , то
, то
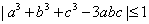 (23)
(23)
Доказательство. Введем обозначения 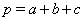 Ваи
Ваи 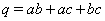 . Тогда
. Тогда 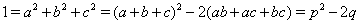 Ваи
Ваи 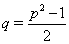 .
.
Используя неравенство Коши-Буняковского (20), можно записать 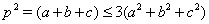 . Так как
. Так как 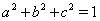 , то
, то 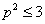 Ваи
Ваи 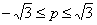 .
.
Имеет место равенство 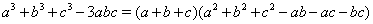 , из которого следует
, из которого следует 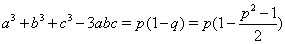 .
.
Следовательно, для доказательства неравенства (23) достаточно показать, что 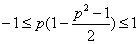 Ваили
Ваили 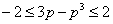 , где
, где 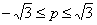 .
.
Пусть 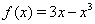 . Для доказательства неравенства (23) требуется показать, что
. Для доказательства неравенства (23) требуется показать, что 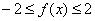 , где
, где 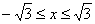 .
.
Так как 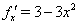 , то корни уравнения
, то корни уравнения 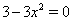 Ваявляются точками, подозрительными на экстремум функции
Ваявляются точками, подозрительными на экстремум функции 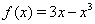 . Уравнение
. Уравнение 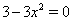 Ваимеет два корня:
Ваимеет два корня: 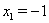 ,
, 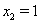 . Поскольку
. Поскольку 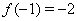 ,
, 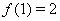 ,
, 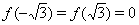 , то
, то 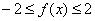 .
.
Отсюда следует, что неравенство (23) доказано.
Пример 13Доказать, если 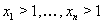 , то
, то
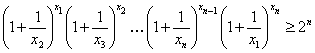
Доказательство. Для получения нижней оценки левой части требуемого неравенства первоначально воспользуемся неравенством Бернулли (18), а затем неравенством Коши (14), тогда
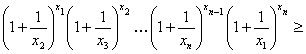
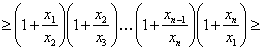
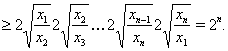
Пример 14Решить уравнение
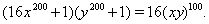 (24)
(24)
Решение. Используя неравенство Коши (14), можно записать
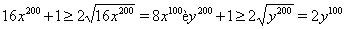
т.е. имеет место неравенство
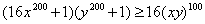
Отсюда и из уравнения (24) следует, что приведенные выше неравенства Коши обращаются в равенства. А это возможно лишь в том случае, когда 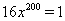 Ваи
Ваи 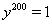 .
.
Следовательно, имеем 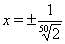 Ваи
Ваи 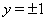 .
.
Ответ: 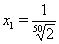 ,
, 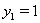 ;
; 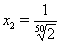 ,
, 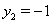 ;
; 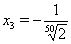 ,
, 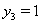 ;
; 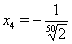 ,
, 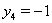 .
.
Пример 15Решить уравнение
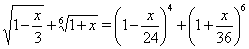 (25)
(25)
Решение. Применим к левой части уравнения (25) неравенство Бернулли (19), а к правой части --- неравенство (18), тогда
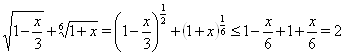
и
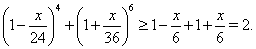
Отсюда следует, что неравенства Бернулли, примененные к обеим частям уравнения (25), обращаются в равенство, а это возможно лишь в том случае, когда 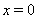 .
.
Ответ: 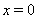 .
.
Пример 16Доказать неравенство
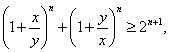 (26)
(26)
Вагде 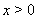 ,
, 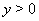 .
.
ВаДоказательство. Непосредственно из неравенства (21) следует 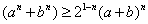 . Используя это неравенство и неравенство Коши (15), получаем неравенство (26) следующим образом:
. Используя это неравенство и неравенство Коши (15), получаем неравенство (26) следующим образом:
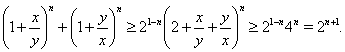
Пример 17Доказать, что
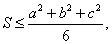 (27)
(27)
где  ,
, 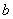 ,
, 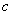 Ва--- стороны треугольника, a
Ва--- стороны треугольника, a 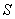 Ва--- его площадь.
Ва--- его площадь.
Доказательство. Известно, что 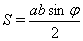 , где
, где 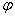 Ва--- угол между сторонами
Ва--- угол между сторонами  Ваи
Ваи 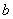 . Поскольку
. Поскольку 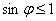 , то
, то 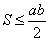 . Используя неравенство Коши
. Используя неравенство Коши 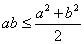 , получаем верхнюю оценку площади треугольника
, получаем верхнюю оценку площади треугольника 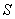 Вавида
Вавида 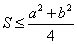 . По аналогии с изложенным выше имеет место
. По аналогии с изложенным выше имеет место 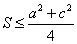 Ваи
Ваи 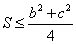 .
.
Тогда 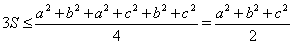 .
.
Отсюда следует справедливость неравенства (27).
Пример 18Доказать, что для всякого прямоугольного параллелепипеда с ребрами 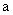 ,
, 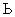 ,
, 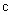 Ваи диагональю
Ваи диагональю 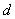 Ваимеет место неравенство
Ваимеет место неравенство
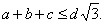 (28)
(28)
Доказательство. Воспользуемся неравенством Коши--Буняковского (20), тогда 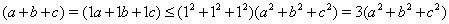 .
.
Поскольку в прямоугольном параллелепипеде 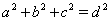 Ва(теорема Пифагора), то
Ва(теорема Пифагора), то 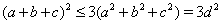 . Отсюда следует справедливость неравенства (28). Заметим, что равенство в (28) достигается тогда и только тогда, когда прямоугольный параллелепипед является кубом.
. Отсюда следует справедливость неравенства (28). Заметим, что равенство в (28) достигается тогда и только тогда, когда прямоугольный параллелепипед является кубом.
Пример 19
Пусть  Ва--- точка, лежащая внутри прямоугольника
Ва--- точка, лежащая внутри прямоугольника  , и
, и 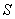 Ва--- его площадь. Доказать, что
Ва--- его площадь. Доказать, что
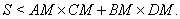 (29)
(29)
Доказательство. Через точку 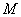 , лежащую внутри прямоугольника
, лежащую внутри прямоугольника 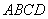 , проведем
, проведем 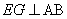 Ваи
Ваи 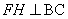 . Обозначим
. Обозначим 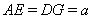 ,
, 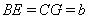 ,
, 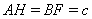 Ваи
Ваи 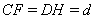 . Тогда
. Тогда 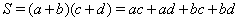 ,
, 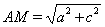 ,
, 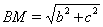 ,
, 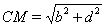 ,
, 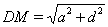 Ваи требуемое неравенство (29) принимает вид
Ваи требуемое неравенство (29) принимает вид
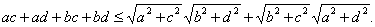 (30)
(30)
Используя неравенство Коши--Буняковского (20), можно записать два неравенства
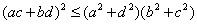
и
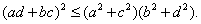
Следовательно, имеет место
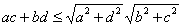
и
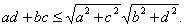
Складывая приведенные выше неравенства, получаем неравенство (30).
4. Методы, основанные на монотонности функцийПри решении уравнений типа 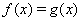 Вав ряде случаев весьма эффективным является метод, который использует монотонность функций
Вав ряде случаев весьма эффективным является метод, который использует монотонность функций 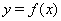 Ваи
Ваи 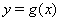 . Если функция
. Если функция 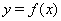 Ванепрерывна и возрастает (убывает) на отрезке
Ванепрерывна и возрастает (убывает) на отрезке 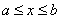 , а функция
, а функция 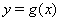 Ванепрерывна и убывает (возрастает) на этом же отрезке, то уравнение
Ванепрерывна и убывает (возрастает) на этом же отрезке, то уравнение 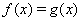 Вана отрезке
Вана отрезке 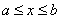 Ваможет иметь не более одного корня.
Ваможет иметь не более одного корня.
Напомним, что функция 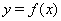 Ваназывается возрастающей (или убывающей) на отрезке
Ваназывается возрастающей (или убывающей) на отрезке 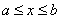 , если для любых
, если для любых 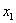 ,
, 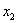 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 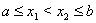 , выполняется неравенство
, выполняется неравенство 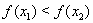 Ва(соответственно,
Ва(соответственно, 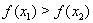 ). Если функция
). Если функция 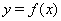 Ваявляется на отрезке
Ваявляется на отрезке 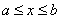 Вавозрастающей или убывающей, то она называется монотонной на этом отрезке.
Вавозрастающей или убывающей, то она называется монотонной на этом отрезке.
В этой связи при решении уравнения 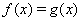 Ванеобходимо исследовать функции
Ванеобходимо исследовать функции 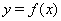 Ваи
Ваи 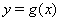 Вана монотонность, и если одна из этих функций на отрезке
Вана монотонность, и если одна из этих функций на отрезке 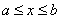 Ваубывает, а другая функция --- возрастает, то необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Если, например, функция
Ваубывает, а другая функция --- возрастает, то необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Если, например, функция 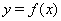 Вавозстает, a
Вавозстает, a 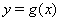 Ваубывает для
Ваубывает для 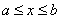 Ваи при этом
Ваи при этом 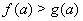 , то корней уравнения
, то корней уравнения 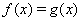 Васреди
Васреди 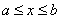 Ванет. Особенно такой метод эффективен в том случае, когда обе части уравнения
Ванет. Особенно такой метод эффективен в том случае, когда обе части уравнения 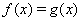 Вапредставляют собой весьма ``неудобные'' для совместного исследования функции. Кроме того, если функция
Вапредставляют собой весьма ``неудобные'' для совместного исследования функции. Кроме того, если функция 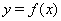 Ваявляется монотонной на отрезке
Ваявляется монотонной на отрезке 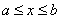 Ваи уравнение
Ваи уравнение 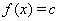 Ва(где
Ва(где 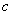 Ва--- некоторая константа) имеет на этом отрезке корень, то этот корень единственный.
Ва--- некоторая константа) имеет на этом отрезке корень, то этот корень единственный.
Задачи и решения
Пример 20Решить уравнение
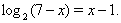 (31)
(31)
Решение. Областью допустимых значений уравнения (31) являются 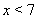 . Рассмотрим функции
. Рассмотрим функции 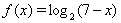 Ваи
Ваи 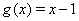 . Известно, что функция
. Известно, что функция 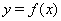 Вадля
Вадля 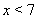 Ваявляется убывающей, а функция
Ваявляется убывающей, а функция 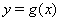 Ва--- возрастающей. В этой связи уравнение (31) может иметь только один корень, т.е.
Ва--- возрастающей. В этой связи уравнение (31) может иметь только один корень, т.е. 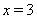 , который легко находится подбором.
, который легко находится подбором.
Ответ: 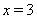 .
.
Пример 21Решить уравнение
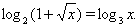 (32)
(32)
Решение. Введем новую переменную 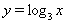 . Тогда
. Тогда 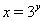 ,
, 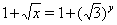 Ваи уравнение (32) принимает вид
Ваи уравнение (32) принимает вид
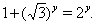 (33)
(33)
Уравнение (33) имеет очевидный корень 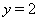 . Покажем, что других корней нет. Для этого разделим обе части уравнения (33) на
. Покажем, что других корней нет. Для этого разделим обе части уравнения (33) на 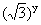 , тогда
, тогда
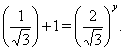 (34)
(34)
Так как 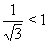 , а
, а 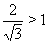 , то левая часть уравнения (34) является убывающей функцией, а правая часть --- возрастающей функцией. Поэтому уравнение (34) если имеет корень, так только один. Ранее было установлено, что
, то левая часть уравнения (34) является убывающей функцией, а правая часть --- возрастающей функцией. Поэтому уравнение (34) если имеет корень, так только один. Ранее было установлено, что 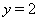 Ва--- корень уравнения (33). Следовательно, этот корень единственный.
Ва--- корень уравнения (33). Следовательно, этот корень единственный.
Таким образом, имеем 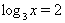 . Тогда единственным корнем уравнения (32) является
. Тогда единственным корнем уравнения (32) является 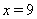 .
.
Ответ: 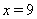 .
.
Пример 22
Решить уравнение
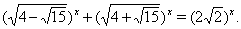 (35)
(35)
Решение. Разделим обе части уравнения (35) на 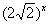 , тогда
, тогда
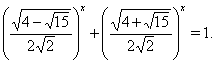 (36)
(36)
Подбором нетрудно установить, что 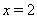 Ваявляется корнем уравнения (36). Покажем, что других корней это уравнение не имеет.
Ваявляется корнем уравнения (36). Покажем, что других корней это уравнение не имеет.
Обозначим  Ваи
Ваи 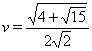 . Очевидно, что
. Очевидно, что 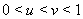 . Следовательно, каждая из функций
. Следовательно, каждая из функций 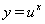 Ваи
Ваи 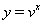 Ваявляется убывающей и при этом
Ваявляется убывающей и при этом 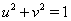 .
.
Если 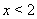 , то
, то 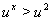 ,
, 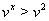 Ваи
Ваи 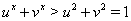 .
.
Если 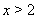 , то
, то 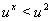 ,
, 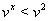 Ваи
Ваи 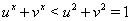 .
.
Следовательно, среди 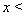 2 или
2 или 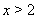 Вакорней уравнения (36) нет.
Вакорней уравнения (36) нет.
Ответ: 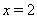 .
.
5. Методы решения функциональных уравненийК числу наиболее сложных задач на вступительных конкурсных экзаменах по математике относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида
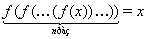 (37)
(37)
или
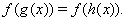 (38)
(38)
Вагде 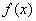 ,
, 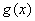 ,
, 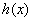 Ва--- некоторые функции и
Ва--- некоторые функции и 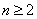 .
.
Методы решения функциональных уравнений (37), (38) основаны на использовании следующих теорем.
Теорема 23
Корни уравнения 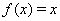 Ваявляются корнями уравнения (37)
Ваявляются корнями уравнения (37)
Доказательство. Пусть 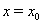 Ва--- корень уравнения
Ва--- корень уравнения 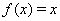 , т.е.
, т.е. 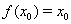 . Тогда справедливы равенства
. Тогда справедливы равенства
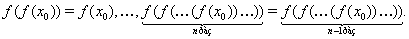
Отсюда следует, что
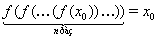
т.е. 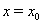 Ваявляется корнем уравнения (37).
Ваявляется корнем уравнения (37).
Теорема 24
Если 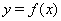 Ва--- возрастающая функция на отрезке
Ва--- возрастающая функция на отрезке 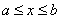 Ваи
Ваи 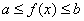 , то на данном отрезке уравнения (37) и
, то на данном отрезке уравнения (37) и 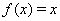 Варавносильны.
Варавносильны.
Доказательство. Пусть 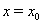 Ваявляется корнем уравнения (37), т.е.
Ваявляется корнем уравнения (37), т.е. 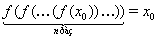 . Предположим, что
. Предположим, что 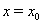 Ване является корнем уравнения
Ване является корнем уравнения 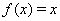 , т.е.
, т.е. 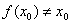 . He нарушая общности рассуждений, будем считать, что
. He нарушая общности рассуждений, будем считать, что 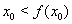 . Тогда в силу возрастания функции
. Тогда в силу возрастания функции 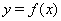 Васправедливы неравенства
Васправедливы неравенства
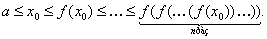
Так как 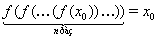 , то из приведенных выше неравенств следует
, то из приведенных выше неравенств следует 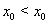 . Таким образом, получили ложное неравенство. А это означает, что
. Таким образом, получили ложное неравенство. А это означает, что 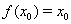 .
.
Отсюда и из теоремы 23 следует справедливость теоремы 24.
Следствие 25
Если функция 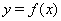 Вавозрастает для любого
Вавозрастает для любого 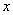 , то уравнения (37) и
, то уравнения (37) и 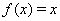 Варавносильны.
Варавносильны.
Следствие 26
Если функция 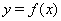 Вавозрастает на своей области определения, то уравнения (37) и
Вавозрастает на своей области определения, то уравнения (37) и 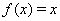 Варавносильны.
Варавносильны.
Более сложным является решение уравнения (37) в том случае, когда на некотором отрезке 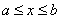 Вафункция
Вафункция 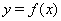 Ваявляется убывающей.
Ваявляется убывающей.
В данном случае имеют место аналоги теоремы 24 и двух следствий только при условии, что в уравнении (37) число 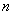 Ванечетное.
Ванечетное.
Теорема 27
Если 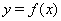 Ва--- убывающая функция на отрезке
Ва--- убывающая функция на отрезке 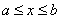 ,
, 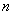 Ва--- нечетное и
Ва--- нечетное и 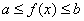 , то на данном отрезке уравнения (37) и
, то на данном отрезке уравнения (37) и 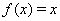 Варавносильны.
Варавносильны.
Доказательство. Пусть 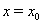 Ваявляется корнем уравнения (37), т.е.
Ваявляется корнем уравнения (37), т.е.
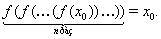
Предположим, что 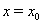 Ване является корнем уравнения
Ване является корнем уравнения 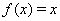 , т.е.
, т.е. 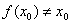 . Не нарушая общности рассуждений, будем считать, что
. Не нарушая общности рассуждений, будем считать, что 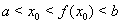 . Тогда в силу убывания функции
. Тогда в силу убывания функции 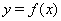 Вана отрезке
Вана отрезке 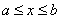 Ваполучаем неравенства
Ваполучаем неравенства 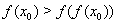 ,
, 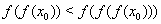 ,
, 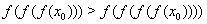 , и т. д.
, и т. д.
Так как 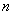 Ва--- нечетное, то
Ва--- нечетное, то 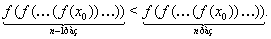
Поскольку 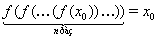 , то из последнего неравенства получаем
, то из последнего неравенства получаем 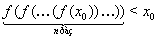 .
.
Так как  Ва--- убывающая функция, то
Ва--- убывающая функция, то 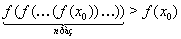 , т.е.
, т.е. 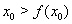 . Получили противоречие тому, что по предположению
. Получили противоречие тому, что по предположению 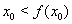 . Следовательно,
. Следовательно, 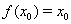 .
.
Отсюда, с учетом теоремы 23, следует справедливость теоремы 27.
Следствие 28
Если функция 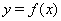 Ваубывает для любого
Ваубывает для любого 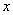 Ваи
Ваи 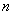 Ва--- нечетное, то уравнения (37) и
Ва--- нечетное, то уравнения (37) и ![]() Вместе с этим смотрят:
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики