Новый метод решения кубического уравнения

Автор: Фильчев Э.Г.

Решение кубического уравнения в системе mn параметров

Решение кубического уравнения на основе современных методов не представляется тривиальным. В любом справочнике по математике предлагаются следующие методы

- разложение левой части на линейные множители ( если возможно )

- с помощью формулы Кардана

- применение специальных таблиц

(см. например, И.Н.Бронштейн. К.А.Семендяев. Справочник по математике тАжМ. Наука 1980. стр.219).

В данной статье рассматривается метод решения любых кубических уравнений включая неприводимый случай формулы Кардана!

Задача "Задано кубическое уравнение вида ax3 + bx2+ cx + d = 0.

Используя формулы системы mn параметров предложить метод определения нулей исходного уравнения ". Пусть а = 1.

Решение

На сайте fgg-fil1.narod.ru/fmat16.doc приведена, полученная автором, формула mn преобразования степенной функции. Для кубического уравнения эта формула имеет вид

(2mn)² + ( 3x + )(2mn) + 3x² + 2bx +с = 0 ( 1 )

где

x - любой из нулей ( корней) исходного уравнения

2mn - разность любой пары из трех нулей исходного уравнения

Решив уравнение (1) относительно х и подставив это значение в исходное уравнение, в результате, после простых, но громоздких преобразований, получим

(2mn)⁶ +2( 3c тАУ b² )(2mn)⁴+(3c тАУ b² )²(2mn)² + [ 4( 3c тАУ b² )³ + ( 2b³ тАУ 9bc + 27d )²]/27 = 0 ( 2 )

Это уравнение устанавливает связь коэффициентов исходного уравнения с параметром (2mn) и является кубическим относительно (2mn)2. На основании формул Виета и уравнения (2) можно сделать следующее утверждение

Утверждение1 "Для любого кубического уравнения вида x3 + bx2+ cx + d = 0 справедливы уравнения

3x2 + 2bx + c = - (2mn)1( 2mn)2

2(3c-b2) = - [(2mn)12+( 2mn)22+( 2mn)32Ва]

[4(3c-b2)3+(2b3 - 9bc+27d)2]/27 = - (2mn)12( 2mn)22( 2mn)32

где (2mn)_j - разность любой пары корней исходного уравнения.

x - один ( любой ) из корней исходного уравнения. "

1. Для любого кубического уравнения вида x3 + bx2+ cx + d = 0 определяем значение

D₁= - 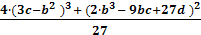Ва= - (2mn)₁² ∙ ( 2mn)₂² ∙ ( 2mn)₃²

2. Определяем значение

D₂ = - 2( 3c тАУ ² ) = - [(2mn)12Ва+ ( 2mn)22Ва+ ( 2mn)32]

Из этих уравнений следует, что

- если выражение - 2(3c - ) - целое число, то оно разложимо на сумму трех квадратов

- и если при этом выполняется равенство D₁ = - (2mn)12( 2mn)22( 2mn)32Ва, то в результате получим решение для (2mn)1,( 2mn)2,( 2mn)3.

3. Определяем значение корней исходного уравнения

3x2 + 2bx + c = - (2mn)1( 2mn)2

3x2 + 2bx + c = (2mn)1( 2mn)2

3x2 + 2bx + c = - (2mn)1( 2mn)3

3x2 + 2bx + c = (2mn)1( 2mn)3

3x2 + 2bx + c = - (2mn)2( 2mn)3

3x2 + 2bx + c = (2mn)2( 2mn)3

Задача решена !

Пример 1 Решить уравнение с помощью формул системы mn параметров

x3 - 9x2+ 23x - 15 = 0

гдеa =1, b = - 9, c = 23, d = -15

Решение

1. Определяем значение D₁ = = -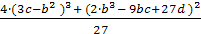

-→ D₁ = - [4(69-81)3+( - 1458 + 1863 - 405)2]/27= - [4(69-81)3+0]/27= 256 = 162

Обратим внимание, что в этом примере (2b3-9bc+27d) = 0

2.Определяем значение D₂= - 2(3c - )

-→ D₂ = - 2( 3∙23 - 81 ) = 24 = 4 + 16 + 4

Это единственное разложение числа 24 на три квадрата. Следовательно

имеем (2mn)₁ = 2, (2mn)₂ = 4, (2mn)₃ = 2.

3. Определяем значение нулей ( корней ) исходного уравнения

3.13x2 + 2bx + c = - (2mn)1( 2mn)2

-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 31 = 0. Нет действительных решений.

3.23x2 + 2bx + c = (2mn)1( 2mn)2

-→ 3x2 - 18x + 23 = -> 3x2 - 18x + 15 = 0 -→ x2 - 6x + 5 = 0

-→ X₁ = 3 + 2 = 5 , X₂ = 3 - 2 = 1

Здесь X₁ = 5 - одно из решений исходного уравнения.

Здесь X₂ = 1 второе решение исходного уравнения.

3.3 3x2 + 2bx + c = - (2mn)1( 2mn)3

-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 27 = 0 -→ x2 - 6x + 9 = 0

-→ X₂ = 3

Здесь X= 3 - последнее из решений исходного уравнения.

3.4 3x2 + 2bx + c = (2mn)1( 2mn)3

-→ 3x2 - 18x + 23 = 2∙2 -→ 3x2 - 18x + 19 = 0. Нет решений исходного уравнения.

Задача решена!

Пример 2 Решить уравнение с помощью формул системы mn параметров

x3 - 20x2+ 113x - 154 = 0

гдеa =1, b = - 20, c =113, d = -154

Решение

1. Определяем значение D₁ = -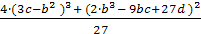

-→D₁ = - [4(339-400)3+( - 16000 + 20340 - 4158)2]/27= - [- 907924+33124]/27=32400

2.Определяем значение D₂ = - 2(3c - )

-→ D₂ = - 2( - 400 ) = 122 = 3² + 7² + 8² = 4² + 5² + 9²

Здесь имеет место два представления числа 122 в виде суммы трех квадратов.

Поэтому, проверяем на соответствие с числом D₁ = 32400.

2.1 3² ∙ 7² ∙ 8² = 28224 ≠ 32400

2.2 4² ∙ 5² ∙ 9² = 32400 . Этот вариант подходит!

-→ (2mn)₁₁ = 4, (2mn)₁₂ = - 4,

(2mn)₂₁ = 5, (2mn)₂₂ = - 5,

(2mn)₃₁ = 9, (2mn)₃₂ = - 9.

3. Определяем значение нулей ( корней ) исходного уравнения

3.13x2 + 2bx + c = - (2mn)1( 2mn)2

-→ 3x2 - 40x + 113 = - 4∙5 -> 3x2 - 40x + 133 = 0.

-→ X₁= 7, X₂ =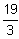

4. Таким образом, определен один из корней исходного кубического уравнения X₁= 7, и кроме того, известны значения (2mn)₁₁ ÷ (2mn)₃₂. Этих данных достаточно для определения двух остальных корней.

4.1 Пусть (2mn)₁₁ = 4 = (X₁ - X₂) -→ X₂ = X₁ тАУ 4 = 7 тАУ 4 = 3. Нет решения(это не корень).

4.2 Пусть (2mn)₁₂ = - 4 = (X₁ - X₂) -→ X₂ = X₁ + 4 = 7 + 4 = 11. Это второй корень.

4.3 Пусть (2mn)₂₁ = 5 = (X₂ - X₃) -→ X₃ = X₂ - 5 = 7 - 5 = 2. Это третий корень.

Решением исходного уравнения будет X₁= 7, X₂= 2, X₃ = 11.

Расчет закончен !

Пример 3 Решить уравнение с помощью формул системы mn параметров

x3 - 10x2 - 49x + 130 = 0

гдеa =1, b = - 10, c = - 49, d = 130

Решение

1. Определяем значение D₁ = -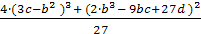

-→D₁ = - [4( -147 - 100)3+( 2000 + 4410 - 3510)2]/27= - [- 60276892+8410000]/27= 1920996

2.Определяем значение D₂ = - 2( 3c - )

-→ D₂ = - 2( - 147 - 100 ) = 494 = 1² + 3² + 22² = 2² + 7² + 21² = 7² + 11² + 18²

Из этих трех вариантов представления числа 494 в виде суммы трех квадратов подходит последний вариант , т.к. 7² ∙ 11² 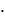Ва18² = 1920996

-→ (2mn)₁₁ = 7, (2mn)₁₂ = - 7,

(2mn)₂₁ = 11, (2mn)₂₂ = - 11,

(2mn)₃₁ = 18, (2mn)₃₂ = - 18.

3. Определяем значение нулей ( корней ) исходного уравнения

3.13x2 + 2bx + c = - (2mn)11( 2mn)21

-→ 3x2 - 20x - 49 = 7∙11 -> 3x2 - 20x - 126 = 0. Эти значения X не подходят!

3.23x2 + 2bx + c = (2mn)11( 2mn)22

-→ 3x2 - 20x - 49 =- 77 -→ 3x2 - 20x + 28 = 0.

-→ X₁ = 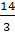, X₂= 2 тАУ это один из корней исходного уравнения!

4. Таким образом, определен один из корней исходного кубического уравнения X₁= 2, и кроме того, известны значения (2mn)₁₁ ÷ (2mn)₃₂. Этих данных достаточно для определения двух остальных корней.

4.1 Пусть (2mn)₁₁ = 7 = (X₁ - X₂) -→ X₂ = X₁ тАУ 7 = 2 тАУ 7 = - 5. Это второй корень!

4.2 Пусть (2mn)₁₂ = - 7 = (X₁ - X₂) -→ X₂ = X₁ +7 = 2 + 7 = 9. Это не корень.

4.3 Пусть (2mn)₂₁ = 11 = (X₁ - X₃) -→ X₃ = X₁ - 11= 2 - 11 = - 9. Это не корень.

4.4 Пусть (2mn)₂₁ = -11 = (X₁ - X₃) -→ X₃ = X₁ + 11= 2 + 11 = 13. Это третий корень!

Решением исходного уравнения будет X₁= 2, X₂= - 5, X₃ = 13.

Расчет закончен !

Пример 4 Решить уравнение с помощью формул системы mn параметров

x3 - 6.85x2 + 13.425x тАУ 8.1 = 0

гдеa =1, b = - 6.85, c = 13.425, d = - 8.1

В этом уравнении имеют место нецелые значения коэффициентов. Это указывает на то, что и корни также могут иметь нецелые значения.

Решение

1. Определяем значение D₁ = -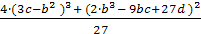

-→D₁ = - [4( 40.275 тАУ 46.9225)3+(- 642.83825 + 827.65125 тАУ 218.7)2]/27

-→D₁ = - [- 1174.9923236875+1148.328769]/27= 0.987539062500

2.Определяем значение D₂ = - 2( 3c - )

-→ D₂ = - 2(40.275 тАУ 46.9225 ) = 13.2950

В этом случае имеют место дробные значения для D₁ и D₂ . Предлагаемый метод решения куб.уравнения оперирует только с целыми числами, поэтому необходимо умножить на 10^k .

При этом значение степени k должно определяться

- для D₂ числом знаков в мантиссе ( для данного примера k₂ = 4 )

- для D₁ =3∙ (число знаков в мантиссе для D₂ ). -→ k₁ = 3∙ k₂ ( для данного примера k₁ = 12 ).

Для дальнейшего рассмотрения используем два числа

- D₁₁ = 987539062500

- D₂₁ = 132950.

3. Далее задача заключается в том, чтобы определить три значения таких целых чисел ( А,Б,Д), при которых выполняются равенства D₂₁ = А² + Б² + Д² и D₁₁ = А² ∙ Б² ∙ Д² .

Для нахождения значений чисел А,Б,Д можно использовать две методики

- найти все варианты представления числа D₂₁ в виде суммы трех квадратов. При этом один из этих вариантов будет соответствовать условию D₂₁ = А² + Б² + Д² и D₁₁ = А² ∙ Б² ∙ Д² .

- найти все варианты представления числа D₁₁ в виде произведения трех квадратов. При этом один из этих вариантов будет соответствовать условию D₂₁ = А² + Б² + Д² и D₁₁ = А² ∙ Б² ∙ Д² .

Вариант D₁₁ = А² ∙ Б² ∙ Д² следует считать более удобным.

Для рассматриваемого примера

D₁₁ = 987539062500 = 250² ∙ 265² ∙ 15²

D₂₁ = 132950 = 250² + 265² + 15².

4. В расчетах п.2 была произведена операция перехода к целым числам путем умножения соответствующих чисел на множители k₁ и k₂ . Совершая обратную операцию, получим

(2mn)₁₁ = 2.5, (2mn)₁₂ = - 2.5,

(2mn)₂₁ = 2.65, (2mn)₂₂ = - 2.65,

(2mn)₃₁ = 0.15, (2mn)₃₂ = - 0.15.

5. Определяем значение нулей ( корней ) исходного уравнения

5.13x2 + 2bx + c = - (2mn)11( 2mn)21

-→ 3x2 - 2∙(6.85)∙ x + 13.425 = (2.5)∙(2.65) -> 3x2 тАУ 13.7x + 6.8 = 0.

-→ X₁= 4 тАУ это один из корней исходного уравнения!

6. Таким образом, определен один из корней исходного кубического уравнения X₁= 4, и

кроме того, известны значения (2mn)₁₁ ÷ (2mn)₃₂. Этих данных достаточно для

определения двух остальных корней.

6.1 Пусть (2mn)₁₁ = 2.5 = (X₁ - X₂) -→ X₂ = X₁ тАУ 2.5 = 4 тАУ 2.5 = 1.5 . Это второй корень!

6.2 Пусть (2mn)₁₂ = - 2.5 = (X₁ - X₂) -→ X₂ = X₁ +2.5 = 4 + 2.5 = 6.5. Это не корень.

6.3 Пусть (2mn)₂₁ = 2.65 = (X₁ - X₃) -→ X₃ = X₁ тАУ 2.65= 4 тАУ 2.65 = 1.35. Это третий корень!

Решением исходного уравнения будет X₁= 4, X₂= 1.5, X₃ = 1.35.

Расчет закончен !

Неприводимый случай формулы Кардана

Если для кубического уравнения имеет место случай одного действительного и двух мнимых сопряженных корней, то такой вариант называют неприводимым случаем формулы Кардана.

Рассмотрим неприводимый случай формулы Кардана с позиций системы mn параметров.

Задача "Задано кубическое уравнение вида ax3 + bx2+ cx + d = 0. Известно, что нули этого уравнения имеют один действительный и два мнимых сопряженных корня . Используя формулы системы mn параметров предложить метод определения нулей исходного уравнения ".

Пусть а = 1.

Решение

Ранее было показано, что для любого кубического уравнения имеют место формулы

D₁= - (2mn)12( 2mn)22( 2mn)32

D₂= - [(2mn)12Ва+ ( 2mn)22Ва+ ( 2mn)32],

где

- (2mn)jВа- разность любой пары корней исходного уравнения

- D₁ = -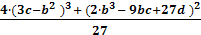

- D₂ = - 2( 3c тАУ ² )

- ( b,c,d) тАУ коэффициенты исходного уравнения.

По условиям задачи имеем один действительный корень ( обозначим его X₁ = g₁) и два сопряженных мнимых корня X₂ =( g₂ - hi), X₃ = ( g₂ + hi). Тогда

(2mn)₁ = ( X₁ - X₂) = (g₁ - g₂ ) + hi

(2mn)₂ = ( X₁ - X₃) = (g₁ - g₂ ) тАУ hi

(2mn)₃ = ( X₂ - X₃) = g₂ - hi - g₂ тАУ hi = - 2hi

-→ D₁= - ( 2mn)₁² ∙ ( 2mn)₂² ∙ ( 2mn)₃² = - [(g₁ - g₂ ) + hi]² ∙ [(g₁ - g₂ ) - hi]² ∙ [2 hi]²

-→ D₁= [(g₁ - g₂ )² + h² ]² ∙ 4h²

Обратим внимание на то, что в этой формуле в квадратных скобках имеют место

- знак тАЬ + тАЬ

- только действительные числа.

Таким образом, метод решения поставленной задачи заключается в следующем

1. На основании значений коэффициентов исходного уравнения по формулам

D₁ = -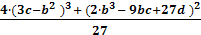

D₂ = - 2( 3c - ² )

определяются значения D₁ и D₂.

2. Определяются D₁ - как произведение двух квадратов

D₂- как удвоенная сумма двух квадратов.

3.Определяются значения g₁, g₂,h.

4. Определяются значения (2mn)₁₁, (2mn)₂₁, (2mn)₃₁

5. Определяются значения корней исходного уравнения.

Пример 5 Решить уравнение с помощью формул системы mn параметров

x3 - 9x2 + 73x тАУ 265 = 0

гдеa =1, b = - 9, c = 73, d = - 265

В этом уравнении имеет место неприводимый случай формулы Кардана.

Решение

1. Определяем значение D₁ = -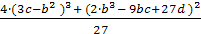

-→D₁ = - [4(219 тАУ 81)3+(- 1458 + 5913 тАУ 7155)2]/27 = - [ 10512288 + 7290000]/27= - 659344

2. Для дальнейших расчетов общий знак тАЬ - тАЬ не имеет значения, поэтому будем рассматривать D₁ как положительную величину.

-→D₁ = [(g₁ - g₂ )² + h² ]² ∙ 4h² = 659344 = 2∙2∙2∙2∙7∙7∙29∙29 = 4∙2∙2∙7∙7∙29∙29= 4∙7² ∙ 58²

Здесь число 659344 представлено в виде всех сомножителей с целью наглядности формирования множителей в соответствии с формулой [(g₁ - g₂ )² + h² ]² ∙ 4h² . Тогда можно записать

h = 7, (g₁ - g₂ )² + h² = 58 -→ (g₁ - g₂ )² = 58 тАУ 49 = 9 -→( g₁ - g₂ ) = В± 3

3. Для определения g₁ и g₂ воспользуемся свойством корней исходного уравнения

- b = X₁+X₂+X₃ -→ - ( - 9) = g₁ + g₂ + hi + g₂ тАУ hi = g₁ + 2 g₂ -→ 9 = g₁ + 2g_2.

4. Теперь, имея два уравнения ( g₁ - g₂ )= В± 3 и (g₁ + 2 g₂) = 9, можно определить значения g₁ и g₂

Пусть ( g₁ - g₂ )= 3 -→ g₂ = g₁ тАУ 3 -→ g₁ + 2(g₁ тАУ 3) = 9 -→ 3g₁ = 15 -→ g₁ = 5 -→g₂ = 2.

-→ X₁ = 5, X₂ = 2 + 7i , X₃ = 2 тАУ 7i

Расчет закончен !

Пример 6 Решить уравнение с помощью формул системы mn параметров

x3 - 30x2 + 322x тАУ 1168 = 0

гдеa =1, b = - 30, c = 322, d = - 1168

В этом уравнении имеет место неприводимый случай формулы Кардана.

Решение

1. Определяем значение D₁ = -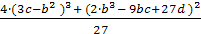

-→D₁ = - [4(966 тАУ 900)3+(- 54000 + 86940 тАУ 31536)2]/27 = - [ 1149984 + 1971216]/27= - 115600

2. Для дальнейших расчетов общий знак тАЬ - тАЬ не имеет значения, поэтому будем рассматривать D₁ как положительную величину.

-→D₁ = [(g₁ - g₂ )² + h² ]² ∙ 4h² = 115600 = 2∙2∙2∙2∙5∙5∙17∙17 = 4∙2∙2∙5∙5∙17∙17= 4∙ 5² ∙34²

Здесь число 115600 представлено в виде всех сомножителей с целью наглядности формирования множителей в соответствии с формулой [(g₁ - g₂ )² + h² ]² ∙ 4h² . Тогда можно записать

h = 5, (g₁ - g₂ )² + h² = 34 -→ (g₁ - g₂ )² = 34 тАУ 25 = 9 -→( g₁ - g₂ ) = В± 3

3. Для определения g₁ и g₂ воспользуемся свойством корней исходного уравнения

- b = X₁+X₂+X₃ -→ - ( - 30) = g₁ + g₂ + hi + g₂ тАУ hi = g₁ + 2 g₂ -→ 30 = g₁ + 2g_2.

4.Теперь, имея два уравнения ( g₁ - g₂ )= В± 3 и (g₁ + 2 g₂) = 30, можно определить значения g₁ и g₂

Пусть ( g₁ - g₂ )= - 3 -→ g₂ = g₁ тАУ 3 -→ g₁ + 2(g₁ тАУ 3) = 30 -→ 3g₁ = 24 -→ g₁ = 8 -→g₂ = 11.

-→ X₁ = 8, X₂ = 11 + 5i , X₃ = 2 тАУ 5i

Расчет закончен !

Новый метод решения кубических уравнений

Из анализа результатов вышеприведенных примеров можно предложить новый метод решения кубических уравнений.Для корней кубического уравнения могут

иметь место следующие случаи

- три корня имеют одинаковые действительные значения

- три корня имеют действительные значения, при этом два из них являются сопряженными, т.е. если X₁ = g + h, то X₂ = g тАУ h или X₁ =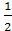Ва(g + h), то X₂ = (g тАУ h), Наличие множителя Ваобусловлено численным значением коэффициента при X для X³ + bX² + cX + d = ( X тАУ X₁)∙( X² + X + c) = 0.

- один корень имеет действительное значение, два других- комплексные и сопряженные, т.е. если X₁ = g + ih, то X₂ = g тАУ ih.

Первый случай тАУ тривиальный . (x тАУ a )³ = x³ тАУ 3ax²+3a²x тАУ a³= 0. Определение корней для остальных случаев является непростой задачей.

Три разных действительных корня

Пусть имеем один действительный корень ( обозначим его X₁ = g₁) и два сопряженных действительных корня. Если исходное уравнение разделить на разность ( X тАУ g₁ ), то получим квадратное уравнение вида

[ X тАУ (g₂ + h)]∙[ X тАУ (g₂ - h)] = 0

-→ X² тАУ 2g₂X + (g₂² тАУ h²) = 0

-→ X₁ = g₁, X_2,3 = g₂ В± h -→ X₂ =( g₂ - h), X₃ = ( g₂ + h)

-→ (2mn)₁ = ( X₁ - X₂) = (g₁ - g₂ ) + h

(2mn)₂ = ( X₁ - X₃) = (g₁ - g₂ ) тАУ h

(2mn)₃ = ( X₂ - X₃) = g₂ - h - g₂ тАУ h = - 2h

-→ D₁ = - ( 2mn)₁² ∙ ( 2mn)₂² ∙ ( 2mn)₃² = - [(g₁ - g₂ ) + h]² ∙ [(g₁ - g₂ ) - h]² ∙ [2h]²

-→ D₁= [(g₁ - g₂ )² - h² ]² ∙ 4h²(3)

-→ D₂ = - [ (2mn)₁² + (2mn)₂² + (2mn)₃² ] = - [(g₁ - g₂ ) + h]² + [(g₁ - g₂ ) - h]² + 4h²

→ D₂ = - [(g₁ - g₂ )² + 2(g₁ - g₂ )∙ h + h² + (g₁ - g₂ )² - 2(g₁ - g₂ )∙ h + h² + 4h²]

→ D₂ = - [ 2(g₁ - g₂ )² + 6h²] = - 2[(g₁ - g₂ )² +3h²] (8)

На основании формул системы mn параметров имеем

D₁ = - 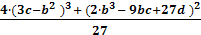Ва(4)

D₂ = - 2( 3c - ² ), (5)

где ,c,d- коэффициенты исходного кубического уравнения.

Три действительных корня и два одинаковых

Пусть имеем один действительный корень ( обозначим его X₁ = g₁) и два равных действительных корня. Тогда имеем h =0 и (2mn)_I = 0

При (2mn)_I = 0 на основании уравнения (1) будем иметь

3x² + 2bx +с = 0 (6)

→ X₂ =( g₂ - h), X₃ = ( g₂ + h) → X₂ = X₃ = g₂

→ (2mn)₁ = ( X₁ - X₂) = (g₁ - g₂ )

(2mn)₂ = ( X₁ - X₃) = (g₁ - g₂ )

(2mn)₃ = ( X₂ - X₃) = g₂ - g₂ = 0

→ D₁= - ( 2mn)₁² ∙ ( 2mn)₂² ∙ ( 2mn)₃² = 0

→ D₂ = - [ (2mn)₁² + (2mn)₂² + (2mn)₃² ] = - [ (2mn)₁² + (2mn)₂² ]

→ D₂ = 2 (2mn)₁² = 2 (g₁ - g₂ )² = - 2( 3c тАУ b² ) = 2( b² тАУ 3c )

→ (g₁ - g₂ )² = ( b² - 3c )

На основании свойств корней исходного уравнения можно записать - =X₁ + 2X₂

→ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа g₁ + 2g₂ = -

Решая систему из двух уравнений будем иметь g₂ = -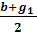

→ВаВаВаВаВаВаВаВаВаВаВаВа X_11,12 = g_11,12= [ - b В± Ва]

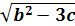→ X_21,22 = g_21,22= [ - В± Ва]

Расчет закончен !

Пример 7 Решить уравнение с помощью формул системы mn параметров

x3 - 41x2 + 475x тАУ 1083 = 0

гдеa =1, b = - 41, c = 475, d = - 1083

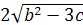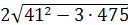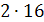1. X_11,12 = g_11,12 = [ - b В± Ва] → X_11,12 = [ 41 В± Ва] = [ 41 В± Ва]

→ X₁₁ = 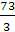Ва, X₁ = 3

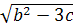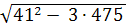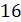X_21,22 = g_21,22 = [ - b В± Ва] → g_21,22 = [ 41 В± Ва]= [ 41 В± Ва]

→ X₂₁ = 19, X₂₂ = 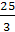Ва→ X₂ = X₃ = 19

Расчет закончен !

Вывод основных формул

Задано исходное уравнение x3 + bx2+ cx + d = 0 . Необходимо найти значения корней.

1. Определяем значение D₁ = -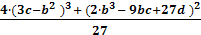

2. Разделим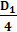

3. Представляем число 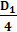Вав виде произведения двух квадратов 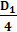= [(g₁ - g₂ )² - h² ]² ∙ h².

4. Меньший множитель принимаем за h²→ [(g₁ - g₂ )² - h² ]² =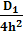

→ (g₁ - g₂ ) = 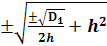Ва(6)

5. Для получения второго уравнения используем свойство корней исходного уравнения

Из исходного уравнения b = - (X₁ + X₂ + X₃ ) → b = - (g₁ + g₂ - h + g₂ +h )

→ = - ( g₁ + 2g₂ ) (7)

6. Решая систему из двух уравнений (26) и (27) в итоге получим

X₁ = g₁= 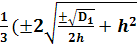Ва- b )

→ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа X₁₁ = g₁₁= 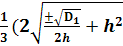Ва- b )ВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)

→ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа X₁₂ = g₁₂= 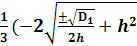Ва- b )ВаВаВаВаВаВаВаВаВаВаВа (9)

Таким образом получили значение одного из корней исходного уравнения.

7.→ g₂ = -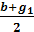

→ g₂₁ = -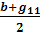

→ g₂₂ = -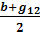

8. Определяем два остальных корня

X₂₁ = g₂₁ + h

X₂₂ = g₂₂ + h

X₃₁ = g₂₁ тАУ h

X₃₂ = g₂₂ тАУ h

Этими формулами определены по два варианта каждого из трех корней. Среди этих вариантов имеют место и корни исходного кубического уравнения.

Задача решена!

Пример 8 Решить уравнение с помощью формул системы mn параметров

x3 - 33x2 + 311x тАУ 663 = 0

гдеa =1, b = - 30, c = 322, d = - 1168

Решение

1. Определяем значение D₁ = -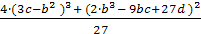

-→D₁ = - [4(933 тАУ 1089)3+(- 71874 + 92367 тАУ 17901)2]/27 = - [- 15185664 +6718464 ]/27=313600

-→ D₁ = [(g₁ - g₂ )² - h² ]² ∙ 4h² = 313600 = 4∙4²∙7²∙10² = 4∙40²∙7² = 4∙70²∙4² = 4∙28²∙10²

313600 = 4∙140²∙2² = 4∙7²∙40² = 4∙5²∙56²

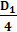-→ Ва= 40²∙7² = 70²∙4² = 28²∙10² = 140²∙2² =5²∙56²

2. Пусть h₁²= 7²

→ X₁ = g₁₁= 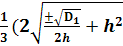Ва- b ) = 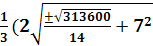Ва- b) =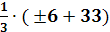

→ g₁₁ =X₁₁ = 13, X₁₂ = 9.

→ g₂₁ = - 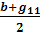Ва= - 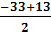Ва= 10

→ X_2,3 = g₂₁ + h₁ = 10 В± 7 → X₂ = 17, X₃ = 3

Задача решена!

Неприводимый случай формулы Кардана

Пусть имеем один действительный корень ( обозначим его X₁ = g₁) и два мнимых сопряженных корня

X₂ =( g₂ - ih), X₃ = ( g₂ + ih).

-→ (2mn)₁ = ( X₁ - X₂) = (g₁ - g₂ ) +ih

(2mn)₂ = ( X₁ - X₃) = (g₁ - g₂ ) тАУ ih

(2mn)₃ = ( X₂ - X₃) = g₂ - ih - g₂ тАУ ih = - 2ih

Задано исходное уравнение x3 + bx2+ cx + d = 0 . Необходимо найти значения корней.

1. Определяем значение D₁ = -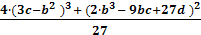

2. Разделим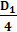

3. Представляем число 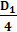Вав виде произведения двух квадратов 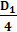= [(g₁ - g₂ )² + h² ]² ∙ h².

4. Меньший множитель принимаем за h²→ [(g₁ - g₂ )² + h² ]² =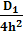

→ (g₁ - g₂ ) =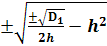

5. Для получения второго уравнения используем свойство корней исходного уравнения

Из исходного уравнения b = - (X₁ + X₂ + X₃ ) → b = - (g₁ + g₂ - ih + g₂ + ih )

→ b = - ( g₁ + 2g₂ )

6. X₁ = g₁= 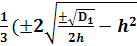Ва- b )

→ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа X₁₁ = g₁₁= 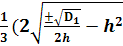Ва- b )

→ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа X₁₂ = g₁₂= 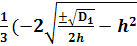Ва- b )

7.→ g₂ = -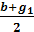

→ g₂₁ = -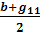

→ g₂₂ = -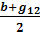

8. Определяем два остальных корня

X₂₁ = g₂₁ + h

X₂₂ = g₂₂ + h

X₃₁ = g₂₁ тАУ h

X₃₂ = g₂₂ тАУ h

Пример 9 Решить уравнение с помощью формул системы mn параметров

x3 - 6x2 + 58x тАУ 200 = 0

гдеa =1, b = - 6, c = 58, d = - 200

Решение

1. Определяем значение D₁ = -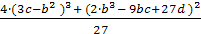

-→D₁ = - [4(174 тАУ 36)3+(- 432 + 3132 тАУ 5400)2]/27 = - [ 10512288 + 7290000 ]/27= 659344

-→ D₁ = [(g₁ - g₂ )² - h² ]² ∙ 4h² = 659344 = 4∙2²∙7²∙29² = 4∙14²∙29² = 4∙7²∙58² = 4∙2²∙203²

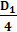-→ Ва= 203²∙2² = 58²∙7² = 29²∙14²

Пусть h₁²= 7²

→ X₁ = g₁₁= 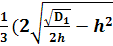Ва- b ) = 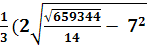Ва+ 6) = 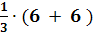Ва= 4

→ X₁ = 4

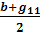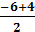→ВаВаВаВаВа g₂₁ = - Ва= - Ва= 1

→ X_2,3 = g₂₁ + ih₁ = 1 В± 7i → X₂ = 1 - 7i, X₃ = 1 + 7i

Задачарешена!

Пример 10 Дано уравнение

x3 - 6x2 + 21x тАУ 52 = 0

где a =1, b = - 6, c = 21, d = - 52

Решить уравнение с помощью формул системы mn параметров

Решение

1. Определяем значение D₁ = -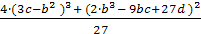

-→D₁ = - [4(63 тАУ 36)3+(- 432 + 1134 тАУ 1404)2]/27 = - [ 78732 + 492804 ]/27= 21168

→ D₁ =[(g₁ - g₂ )² - h² ]² ∙ 4h² = 21168 = 4∙2²∙7² ∙ 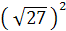Ва= 4∙14²∙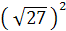Ва= 4∙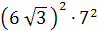

→ D₁ =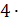

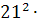
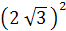
Пусть h₁²=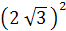

→ X₁ = g₁₁= 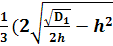Ва- b ) = 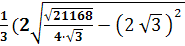Ва+ 6) = 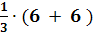Ва= 4

→ X₁ = 4

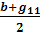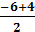→ВаВаВаВаВа g₂₁ = - Ва= - Ва= 1

→ X_2,3 = g₂₁ + ih₁ = 1 В± 2i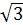Ва→ X₂ = 1 + 2i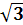Ва, X₃ = 1 - 2i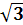

Сравните метод решения и результат с первоисточником.

[И.Н.Бронштейн. К. А.Семендяев .Справочник по математике. М. Наука.1980. Стр. 220 ]

Вывод новых формул

Основные свойства корней квадратного и кубического уравнений выражаются известными формулами Виета. Использование системы mn параметров дает возможность получения новых, ранее неизвестных, формул отражающих свойства корней указанных уравнений.

Рассмотрим кубическое уравнение и проведем анализ формулы (1)

(2mn)² + ( 3x + )(2mn) + 3x² + 2bx +с = 0

Если в это уравнение подставить значение любого из корней исходного кубического уравнения, то получим

(2mn)² + ( 3x_i + )(2mn) + 3x_i² + 2bx_i +с = 0

→ (2mn)² + ( 3x₁ + )(2mn) + 3x₁² + 2bx₁ +с = 0

→ (2mn)² + ( 3x₂ + )(2mn) + 3x₂² + 2bx₂ +с = 0

→ (2mn)² + ( 3x₃ + )(2mn) + 3x₃² + 2bx₃ +с = 0

Таким образом, исходное кубическое уравнение распадается на три квадратных уравнения. При этом для каждого положительного значения (2mn)_Iобязательно найдется отрицательное значение (2mn)_j. Поэтому общая сумма всех корней вида (2mn) будет равна нулю.

→ ( 3x₁ + ) + ( 3x₂ + ) + ( 3x₃ + ) = 0 → 3( x₁ + x₂ + x₃ ) = - 3

→ ( x₁ + x₂ + x₃ ) = - .

Таким образом получили строгое доказательство одного из уравнений Виета.

Рассмотрим любых два уравнения, например,

→ (2mn)² + ( 3x₁ + )(2mn) + 3x₁² + 2bx₁ +с = 0

(2mn)² + ( 3x₂ + )(2mn) + 3x₂² + 2bx₂ +с = 0.

Здесь в качестве свободных членов имеем 3x₁² + 2bx₁ +с и 3x₂² + 2bx₂ +с. Их сумма равна

→ Σ = 3(x₁² + 3x₂²) + 2(x₁ + x₂ ) + 2 с. Расчеты показывают, что

3(x₁² +x₂²) + 2( x₁ + x₂ ) + 2 с = ( x₁ - x₂ )²

→ (x₁ + x₂)² + ( x₁ + x₂ ) + с - x₁∙ x₂ = 0

Тогда для трех корней исходного уравнения будем иметь

→ВаВаВаВаВа (x₁ + x₂)² + ( x₁ + x₂ ) + с - x₁∙ x₂ = 0

→ВаВаВаВаВа (x₁ + x₃)² + ( x₁ + x₃ ) + с - x₁∙ x₃ = 0

→ (x₂ + x₃)² + ( x₂ + x₃ ) + с - x₂∙ x₃ = 0

Это новые формулы, отражающие свойства корней исходного кубического уравнения!

В общем случае эта формула имеет вид

( x_i + x_j)² + ( x_i + x_j ) + с - x_i∙ x_j= 0 ( 10 )

Пример 11 Проверить формулу ( 10 )

x3 - 20x2+ 113x - 154 = 0

где a =1, b = - 20, c =113, d = -154

Здесь X₁= 7, X₂= 2, X₃ = 11.

→ (x₁ + x₂)² + ( x₁ + x₂ ) + с - x₁∙ x₂ = 0 → (7 + 2)² - 20( 7 + 2 ) + 113 - 7∙ 2= 0

→ (x₁ + x₃)² + ( x₁ + x₃ ) + с - x₁∙ x₃ = 0 → (7 + 11)² - 20( 7 + 11 ) + 113 - 7∙ 11= 0

→ (x₂ + x₃)² + ( x₂ + x₃ ) + с - x₂∙ x₃ = 0 → (2 + 11)² - 20( 2 + 11 ) + 113 - 2∙ 11= 0

Расчет подтверждает верность формулы ( 10 ).

Три действительных корня и два одинаковых

При наличии двух одинаковых корней имеет место нулевая разность, т.е. (2mn) = 0.

Тогда из уравнения (2) следует 3x₁² + 2bx₁ +с = 0. Подставив значения коэффициентов и с и решив это уравнение получим значение корня- дубля.

Пример 12 Пусть имеемв качестве исходногоуравнение x³ тАУ 25x² + 203x тАУ 539 = 0. Необходимо найти решения данного уравнения.

Решение Допустим, что для данного уравнения имеют место два одинаковых корня. Тогда имеем 3x₁² + 2bx₁ +с = 0 → 3x₁² - 50x₁ + 203 = 0 → x_1,2 = 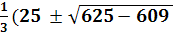Ва) → x₁ = 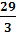Ва, x₂ = 7.

Подставив значение x = 7 в исходное уравнение, убеждаемся, что это один из корней- дубля исходного уравнения. Определить третий корень исходного уравнения не представляет особого труда. Таким образом, решением заданного исходного уравнения является

XВместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики