Основи теорii графiв. Властивостi ойлерових та гамiльтонових графiв

КУРСОВА РОБОТА

з дисциплiни

тАЮАлгебра та теорiя чиселтАЭ

за темою

тАЮОснови теорii графiв.

Властивостi ойлерових та гамiльтонових графiвтАЭ

ЗМРЖСТ

ВСТУП

РОЗДРЖЛ РЖ ВВЕДЕННЯ В ТЕОРРЖЮ ГРАФРЖВ

1.1 Основнi поняття та означення

1.2 Лема про рукостискання

1.3 Оцiнки для числа ребер з 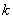Вакомпонентами зв тАШязностi

1.4 Орiiнтованi графи, графи з петлями, графи з паралельними дугами

РОЗДРЖЛ РЖРЖ ОЙЛЕРОВРЖ ГРАФИ

2.1 Ойлерова ломиголовка ВлКенiгзберзьких мостiвВ»

2.2 Основнi поняття та означення ойлерових графiв

2.3 Приклади ойлерових графiв

РОЗДРЖЛ РЖРЖРЖ ГАМРЖЛЬТОНОВРЖ ГРАФИ

3.1 Сутнiсть гамiльтонових графiв

3.2 Основнi поняття та означення

3.3 Приклади гамiльтонових графiв

ВИСНОВКИ

СПИСОК ВИКОРИСТАНОРЗ ЛРЖТЕРАТУРИ

ВСТУП

Роком виникнення теорii графiв одностайно вважаiться рiк 1736, коли Леонард Ойлер опублiкував розвтАЩязок так званоi задачi про кенiгсберзькi мости, а також знайшов загальний критерiй iснування ойлерового циклу в графi.

Отримання дальших суттiвих результатiв у цiй галузi датують серединою ХIХ столiття. Однак початок проведення активних систематичних дослiджень та становлення теорii графiв як окремiшного авторитетного роздiлу сучасноi математики вiдбулося ще майже 100 рокiв по тому, тобто в серединi ХХ столiття. Саме з цього часу граф стаi однiiю з найпоширенiших i найпопулярнiших математичних моделей у багатьох сферах науки i технiки. Картинка у виглядi набору точок на площинi та лiнiй, проведених мiж деякими з них, стала зручною i наочною формою зображення найрiзноманiтнiших обтАЩiктiв, процесiв та явищ.

Великою мiрою це повтАЩязано з виникненням, бурхливим розвитком та поширенням електронних обчислювальних машин i, як наслiдок, значним зростанням ролi задач дискретного характеру. Математика вiд "обслуговування" переважно фiзики переходить до проникнення своiх методiв у iншi сфери людськоi дiяльностi. Одним з потужних iнструментiв такого проникнення i граф.

РЖз суто формальноi точки зору граф можна розглядати як один з рiзновидiв алгебраiчноi системи (а саме, як модель), а отже, i всю теорiю графiв - як роздiл сучасноi алгебри. Справдi, результати та методи алгебри широко використовуються в теорii графiв. Однак за останнi пiвстолiття активного iнтенсивного та екстенсивного розвитку теорiя графiв виробила свою достатньо специфiчну власну проблематику i методологiю. На сьогоднi теорiя графiв i однiiю зi складових математичного апарату кiбернетики, важливим роздiлом дискретноi математики.

ВаВ курсовi роботi дослiдженi властивостi ойлерових та гамiльтонових ланцюгiв та циклiв в теорii графiв, а також наведенi приклади графiв.

РОЗДРЖЛ РЖВВЕДЕННЯ В ТЕОРРЖЮ ГРАФРЖВ

1.1 Основнi поняття та означення

Основнi елементи геометричних фiгур, якi застосовуються у теорii графiв наведенi на рис.1. та складаються з вершин графу, ребер графу та дуг графу.

Сполучення цих елементiв визначаi поняття: неорiiнтований граф, орiiнтований граф та змiшаний граф [6].

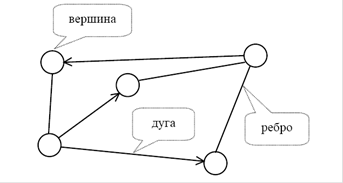
Рис.1.1. Основнi елементи графу (вершина, ребро, дуга)

Неорiiнтований граф (неограф) тАФ це граф (рис.1.2), для кожного ребра якого несуттiвий порядок двох його кiнцевих вершин.

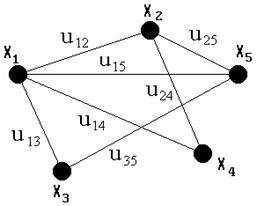
Рис.1.2. Неорiiнтований граф (вершини та ребра)

Орiiнтований граф (орграф) тАФ це граф, для кожного ребра якого iстотний порядок двох його кiнцевих вершин. Орграф представлений на рис.1.3, ребра орграфа iнодi називають дугами.

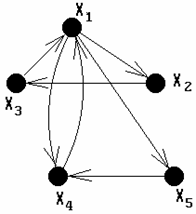
Рис. 1.3. Орiiнтований граф

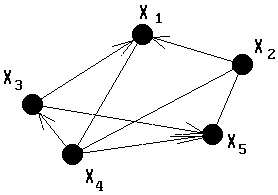
Рис. 1.4. Змiшаний граф

Змiшаний граф (рис.1.4) тАУ це граф, що мiстить як орiiнтованi, так i неорiiнтованi ребра. Кожноi з перерахованих видiв графа може мiстити одне або кiлька ребер, у яких обидва кiнцi сходяться в однiй вершинi, такi ребра називаються петлями (рис.1.5).

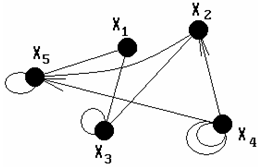
Рис. 1.5. Змiшаний граф з петлями

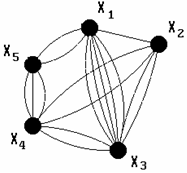
Рис. 1.6. Загальний випадок графа

У загальному випадку множина ребер може складатися iз трьох непересiчних пiдмножин: пiдмножини ланок, пiдмножини дуг i пiдмножини петель (рис.1.6).

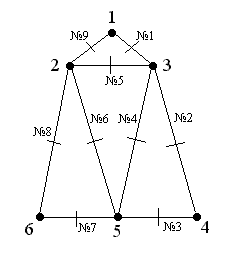
Рис.1.7. Сутнiсть геометричноi конфiгурацii графа, в якому всi вершини можна обiйти за маршрутом без перетинання ребер графу

Наочно граф можна уявляти як геометричну конфiгурацiю ( див. рис.1.7), яка складаiться з точок (вершин графу 1,2,3,4,5,6) i ребер (лiнiй або вiдрiзкiв №1(1-3), №2(3-4), №3(4-5), №4(3-5), №5(2-3), №6(2-5), №7(5-6), №8(6-2), №9(2-1), якi сполучають деякi точки (вершини) за вибраним алгоритмом обходу вершин графу) [5].

Дамо формальне математичне означення графа згiдно [11].

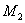Нехай тАУдеяка скiнченна множина (множина вершин),Ва- множина всiх невпорядкованих пар елементiв (ребер або дуг графу) з множини вершин, .

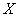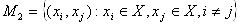Означення 1.1.

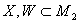Граф ВатАУ пара множин. Множина 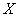тАУце множина вер-шин, множина 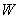тАУце множина ребер. Якщо 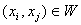, то ми говоримо, що ребро 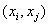Васполучаi вершину 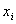Ваз вершиною 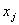; iнша термiнологiя тАУ ребро 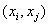Ваi вершини 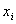Вата 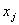Ва- iнцидентнi.

Означення 1.2.

Граф називаiться повним , якщо 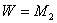, тобто граф складаiться з максимально можливоi кiлькостi ребер, якi попарно зтАЩiднують точки 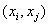Вайого вершин (див.рис.1.8). Якщо множина 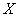Вамiстить 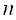Вавершин, то, очевидно , число ребер повного графа дорiвнюi .

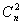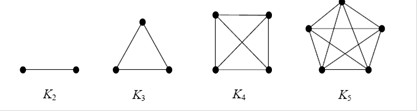
Рис.1.8. Приклади повних графiв

Означення 1.3.

Граф називаiться порожнiм, якщо 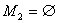, тобто граф не маi ребер (див.рис.1.9).

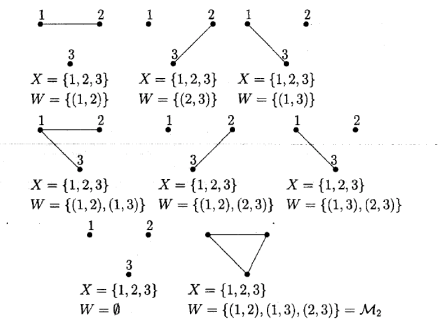
Рис.1.9. Приклад побудови 3-х вершинного графу з рiзною кiлькiстю ребер (заповнення графу вiд ВлпорожньогоВ» до ВлповногоВ»)

Природно виникаi питання: скiльки i рiзних графiв з множиною вершин 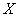Ва, якщо 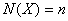. Для цього доведемо наступну теорему.

Теорема 1.1.

Число усiх рiзних графiв з 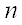Вавершинами дорiвнюi (табл.1.1):

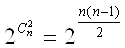
Доведення. Справдi, граф Ваповнiстю визначено, якщо вказано множину 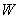, яка i пiдмножиною 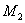. Множина 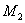Вамiстить 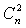Ваелементiв, тому число усiх ii пiдмножин дорiвнюi 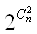Ва.

Таблиця 1.1

Зображення повних графiв з кiлькiстю вершин вiд 5 до 11 [3]

Означення 1.4.

Вершини 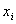Вата 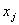Ваграфа Ваiнцидентнi, якщо .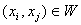

Означення 1.5.

Степенем 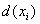Вавершини 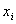Ваграфа Ваназиваiться число вершин 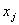, якi iнцидентнi вершинi 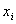Ва( число вiдрiзкiв якi виходять з вершини 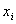) тАУ див.рис.1.10.

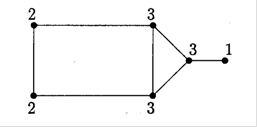
Рис.1.10. Визначення степенiв вершин графу по кiлькостi ребер, що виходять iз вершин

Означення 1.6.

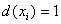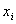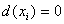Якщо , то вершина Ваназиваiться кiнцевою вершиною графа . Якщо , то вершини 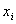Ваназиваiться iзольованою(див рис. 1.11)

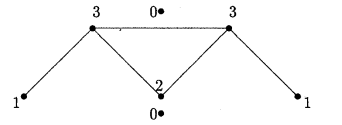
Рис.1.11. Визначення кiнцевих та iзольованих вершин графа

1.2 Лема про рукостискання

Формулювання цiii леми просте тАУ тАЮкiлькiсть рук, що приймають участь у рукостисканнi N-пар людей, дорiвнюi 2*NтАЭ. Лему можна представити у формi графу, де N вершин зтАЩiднанi ребрами d(x_i,x_j) рукостискання i та j тАУ вершин (див. рис.1.12), виконавши наступне доведення.

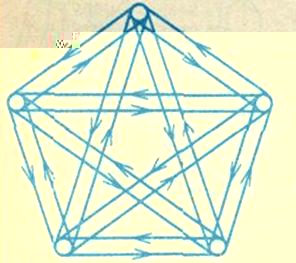
Рис.1.12. тАЮЛема про рукостисканнятАЭ 5 осiб у виглядi графу тАЮвзаiмно-простягнутих руктАЭ (10 пар рук для повноi множини рукостискань) [3]

Нехай Ваграф з множиною верщин . Тодi

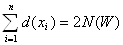Ва(1.1)

Доведення. Зауважимо,що кожне ребро графа в сумi 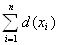Вавраховуiться двiчi (див. рис.1.5), i тому спараведива рiвнiсть (1.1). Зауважимо, що сума сту-пенiв усiх вершин у графi (або мультiграфi без петель) повинна бути парною. Це випливаi з того, що якщо взяти вершини, взагалi не пов'язанi одна з одною, то сума ступенiв цих вершин дорiвнюi нулю. Додаючи будь-яке ребро, що пов'язуi двi вершини, збiльшуiмо суму всiх ступенiв на 2 одиницi. Таким чи-ном, сума всiх ступенiв вершин парна. З рiвностi 1.1 випливаi такi твердження: число вершин непарного степеня в графi обовязково i парним числом.

Для визначення матрицi сумiжностi, розглянемо граф . Нехай

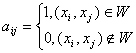
Означення 1.7.

Матриця 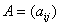називаiться матрицею сумiжностi ( iнцидентностi) графа .

Матриця сумiжностi - це симетрична матриця, елементи якоi до-рiвнюють нулевi або одиницi ( дiагональнi елементи дорiвнюють нулевi) i така, що сума чисел в будь-якому рядку i будь-якому стовпцi дорiвнюi степенi вiд-повiдноi вершини. Так, для графу, наведеного на рис.1.13, матриця сумiжностi побудуiться у виглядi:

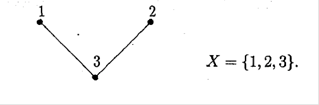
Рис.1.13. До побудови матрицi сумiжностi 3-х вершинного графу

Означення 1.8.

Послiдовнiсть ребер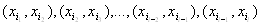, в якiй сусiднi ребра iнцидентнi однiй i тiй же вершинi називаються ланцюгом. Ланцюг називаiться простим, якщо всi вершини, належнi йому (крiм, можливо, першоi i останньоi), рiзнi; число в цьому випадку називають довжиною ланцюга.

Якщо 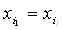Ва, то ланцюг називаiться циклом. Цикл, в якому всi вершини рiзнi, називаiться простим. Приклади простих ланцюгiв та простих циклiв наведенi на рис.1.14:

(1,3), (3,4), (4,6) тАУ простий ланцюг;

(1,2), (2,5), (5,6) тАУ простий ланцюг;

(1,3), (3,4), (4,6), (6,5), (5,2)Ю (2,1) тАУ простий цикл.

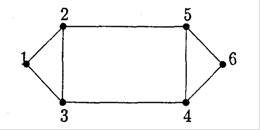
Рис 1.14. Приклад графа з простими ланцюгами та простими циклами

Означення 1.9.

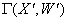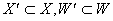Граф i пiдграфом графа , якщо .Якщо 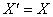Ва, то пiдграф 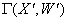Ваназиваiться остовним пiдграфом.

Означення 1.10.

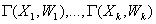Граф Ваi сумою графiв , якщо

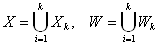
ця сума називаiться прямою, якщо ,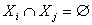

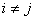
1.3 Оцiнки для числа ребер з 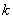Вакомпонентами зв тАШязностi

Означення 1.11.

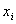Граф називаiться зв язним , якщо будь-якi вершини Вата 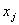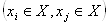Васполученi ланцюгом з початком в 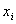Ваi кiнцем в 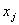. З симетрii випливаi, що в цьому випадку i вершина 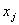Васполучена з вершиною .

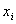Теорема 1.2.

Кожен граф i прямою сумою зв язних графiв.

Доведення. На множинi вершин 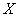Ваграф визначимо вiдношення

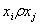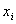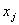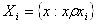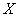, якщо Васполучаiться з Ва.Вiдношення Ваi вiдношенням еквiвалентнос-тi. Позначимо через .Тодi Ваi i розбиття Вана класи еквiвалентностi. Графи 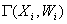Ваi зв язними графами i

Ва(1.2)

i прямою сумою звтАЩязних графiв.

Цi графи називаються компонентами звтАЩязностi.

Розглянемо оцiнки для числа ребер з 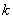Вакомпонентами звтАЩязностi.

Теорема 1.3.

Нехай граф, який складаiться з 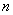Вавершин, 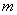Варебер i 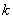компонент зв язностi. Тодi виконуються нерiвностi

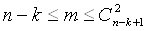
Доведення . Доведемо спочатку нерiвнiсть 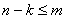.Будемо доводити iндукцiiю за числом ребер. Припустимо, що нерiвнiсть справедлива для всiх графiв з числом ребер 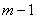. Нехай граф з 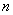вершин, 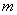Варебер i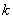

компонентами звтАЩязностi. Викреслимо максимальне можливе число ребер так, щоб не змiнювалося число компонент звтАЩязностя. Число ребер в отриманому графi позначемо .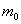

Розглянемо для прикладу граф, зображений на рисунку (1.15)

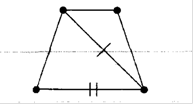
Рис. 1.15. Приклад 1 графу для оцiнки звтАЩязностi

В ньому 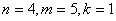.Викресливши два ребра, отримаiмо граф 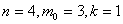. Викреслити далi яке-небудь ребро, не порушуючи зв язностi, вже не можна (див.рис.1.16).

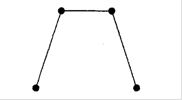
Рис. 1.16. Приклад 1 графу для оцiнки звтАЩязностi

Повернемося до графу, отриманого з . Викресливши в ньому ще одне ребро, ми отримаiмо граф з числом компонент зв язностi на одиницю бiльшим. В силу iндуктивного припущення, справедливого, бо 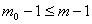, маiмо 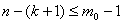Ва, звiдки .

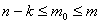Для доведення верхньоi оцiнки в нерiвностi (1.3) замiнимо кожну компо-ненту повним графом. Нехай 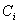Вата 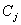Вадва повних, отриманих з компонент звтАЩ язностi 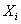Ват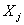а Ва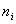, а Вата 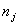Вачисло ребер в цих компонентах 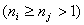. Замiнемо 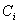Вана повний граф, додавши одну вершину, а 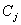Вазамiнемо на повний граф, вiднявши одну вершину. Тодi загальне число вершин не змiнеться, а число ребер збiльшиться на додатню величину

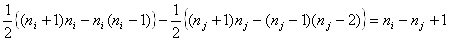
Отже, для того, щоб число ребер у графi було максимально можливим (при фiксованих 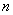Ваi 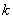), граф повинен складатись з 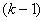Ваiзольованих вершин i повного графа з 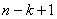Вавершинами.Звiдси й випливаi нерiвнiсть (1.3). Теорема доведена.

З нерiвностi (1.3) випливаi такий наслiдок.

Наслiдок. Будь-який граф з 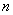Ваi бiльше нiж 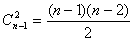Варебрами i звтАЩязним.

Справдi, якщо граф з 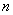Вавершинами маi двi компоненти звтАЩязностi, то максимальне число ребер не перевищуi .

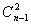Найти компоненти сильноi звтАЩязностi графу на рис.1.17.

Вiдповiдi

Рис.1.17. 7-ми вершинний граф для обчислення компонентiв звтАЩязностi [10]

1.4 Орiiнтованi графи, графи з петлями, графи з паралельними дугами

Дамо означення орiiнтованих графiв, графiв з петлями та графiв з пара-лельними дугами.

Неформально, граф виглядаi як дiаграма, тобто множина точок площини (вершин, або вузлiв), зтАЩiднаних мiж собою лiнiями (ребрами). Дiаграма даi уяву про звтАЩязки мiж елементами (вершинами), але нiчого не каже про метричнi властивостi (довжина лiнiй, iх форма тощо).

Залежно вiд типу ребер вiдрiзняють кiлька типiв графiв. Петля тАФ це реб-ро, що зтАЩiднуi вершину саму з собою. У мультиграфi петлi не допускаються, але пари вершин можуть зтАЩiднуватися кiлькома ребрами, якi називаються крат-ними, або паралельними. У псевдографi допускаються петлi й кратнi ребра. В звичайному графi немаi нi петель, нi кратних ребер.

За допомогою графiв подаються структурнi залежностi мiж елементами, вiдповiдний граф називаiться орiiнтованим, або орграфом, а його орiiнтованi ребра тАФ дугами. Граф, що маi орiiнтованi та неорiiнтованi ребра одночасно, називаiться змiшаним.

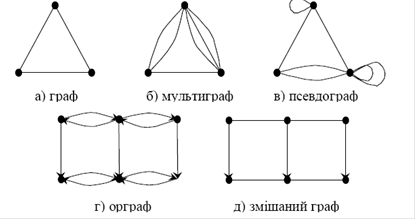
Рис.1.18. Види орiiнтованих графiв

Означення 1.12.

Нехай 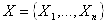Вамножина вершин , Ва- множина впорядкованих пар елементiв з 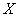Ва( будемо називати iх дугами).Орiiнтованим графом Ваназиватимемо пару множин 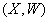Ва, де .

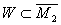Дуга 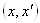Ваназиваiться дугою з 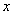Вав 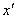Ва(див.рис.1.19).

Рис. 1.19. Орiiнтований 3-х вершинний граф (,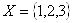

.)

Теорема 1.4. Число усiх орiiнтованих графiв з 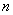Вавершинами дорiвнюi .

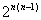Доведення . Справдi , число впорядкованих пар елементiв з 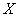Вадорiвнюi 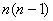, тому число всiх можливих множин дуг дорiвнюi .

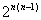Означення 1.13.

Нехай -множина вершин. Орiiнтованим графом з петлями будемо називати пару множин 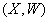, де 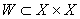Ва(див.рис.1.20).

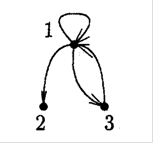
Рис.1.20. Орiiнтований граф з петлями в якому ,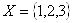

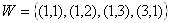
Теорема 1.5. Число орiiнтованих графiв з петлями , якi мають 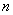Вавершин, дорiвнюi .

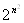Доведення. Справдi, число рiзних множин 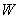(пiдмножин множини 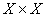) дорiвнюi .

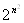Якщо розглядаiться одночасно декiлька типiв графiв, то графи якi описуються означення (1.1), будемо називати простими графами.

Якщо в означеннi (1.1) до множини 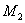Ваневпорядкованих пар приiднати ще множину всiх пар виду 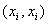, то вiдповiдний граф називаiться простим графом з петлями.

З теореми 1.5 випливаi довiд теореми 1.6 про простi графи.

Теорема 6. Число всiх простих графiв з 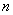Вавершинами i петлями дорiвнюi

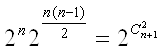
Надалi, ми будемо розглядати простi графи.

РОЗДРЖЛ РЖРЖОЙЛЕРОВРЖ ГРАФИ

2.1 Ойлерова ломиголовка ВлКенiгзберзьких мостiвВ»

Для рiшення серйозних математичних задач математик Ойлер(Euler) використовував наочнi ломиголовки. Одна з них поклала початок зовсiм новiй областi дослiджень, що виросла згодом у самостiйний роздiл математики - теорiю графiв i топологiю. Особливiсть цiii теорii - у геометричному пiдходi до вивчення об'iктiв.

Теорiя графiв тАУ одна з небагатьох математичних дисциплiн, дата народження якоi може бути встановлена абсолютно точно.

Перша робота з теорii графiв належить Леонарду Ойлеру. Вона зтАЩявилась в публикацiях Санкт-Петербургзськоi Академii наук у 1736 роцi.

Праця Ойлера розпочиналася з розгляду однiii ломиголовки так званоi тАЮзадачi про кенiгзберзькi моститАЭ

Мiсто Кенiгзберг (нинi Калiнiнград) розташоване на берегах рiчки Прегель i двох островах. Рiзнi частини мiста сполученi сiмома мостами. Щонедiлi жителi мiста любили здiйснювати прогулянки по мiсту. Ойлер поставив питання: чи можна здiйснити прогулянку, вийшовши з дому i повернувшись до нього , таку , щоб по кожному мосту пройти рiвно один раз.

Сформулюiмо задачу, як задачу теорii графiв. Схематична карта мiста зображена на рисунку 2.1.

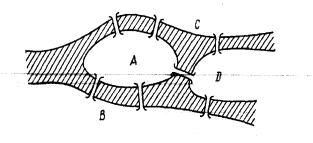
Рис. 2.1. Схема мостiв в Кенiгзберзi [11]

Чотири частини мiста зображенi лiтерами 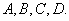ВаОскiльки нас цiкав-лять лише переходи через мости, ми можемо вважати 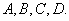Вавершинами графа, ребра якого вiдповiдають мостам. Цей граф зображено на рисунку 2.2.

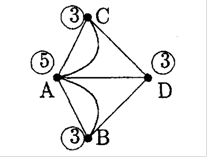
Рис. 2.2. Граф ВлКенiгзберзьких мостiвВ» в ломи головцi Ойлера

Ойлер зауважив, що цей граф не являi iдиного циклу; з якоi б вершини ми не почали б обхiд , ми не можемо обiйти весь граф i повернутись назад, не проходячи жодного ребра двiчi. Якби такий цикл iснував, то з кожноi вершини виходило б стiльки ребер , скiльки в неi входить , iнакше кажучи степiнь кожноi вершини була б парним числом. Таким чином, вiдповiдь на питання Ойлера-негативна.

Виклавши розв язання задачi про кенiгзберзькi мости , Ойлер в своiй працi поставив питання : на яких графах можна знайти цикл, який мiстить всi ребра графа, при чому кожне ребро зустрiчаiться в циклi рiвно один раз?

Це дало початок системному математичному пiдходу до побудови та вивчення властивостi графiв.

2.2 Основнi поняття та означення ойлерових графiв

Означення 2.1

ЗвтАЩ яний граф називаiться ойлеровим графом, якщо iснуi замкнений ланцюг, який проходить через кожне ребро.Такий ланцюг будемо називати ойлеровим ланцюгом, або ойлеровим циклом (див.рис.2.3)

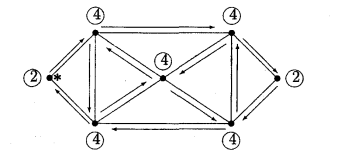
Рис.2.3. Структура вершин та ребер в неорiiнтованому ойлеровому графi (* - означено точку входу ойлерового ланцюга - циклу)

Означення 2.2

Граф називаiться напiвойлеровим, якщо iснуi ланцюг , який проходить через кожне його ребро рiвно один раз (див рис.2.4).

Рис.2.4. Структура вершин та ребер в неорiiнтованому напiвойлеровому графi (* - означено точку початку та кiнця ойлерового ланцюгу)

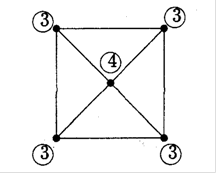
Рис.2.5. Приклад неойлерового графу

Дослiдивши структуру неойлерового графу, наведеного на рис.2.5, розг-лянемо необхiднi i достатнi умови для того, щоб граф був ойлеровим. Доведемо лему, яка далi буде грати iстотну роль.

Лема 2.1

Якщо степiнь кожноi вершини графа Ване менше двох , то граф мiстить цикл.

Доведення. Якщо в графi i петлi або кратнi дуги, то твердження леми оче-видне. Тому надалi будемо припускати , що Ваi простим графом. Нехай 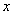тАУ довiльна вершина графа . Побудуiмо по iндукцii маршрут

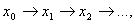
обираючи вершину 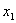, сумiжну з 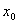, а при 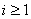Ваобираючи вершину 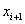, сумiж-ну з 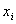Ваi вiдмiнну вiд 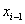Ва(iснування такоi вершини випливаi з умови леми). Оскiльки Вамаi скiнченне число вершин, то врештi-решт ми прийдемо до вершини 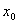, з якоi вийшли. Отримаiмо цикл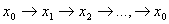

Лема доведена.

Теорема 2.1 Для звтАЩязного графа Ванаступнi умови еквiвалентнi:

1. - ойлерiв граф;

2. кожна вершина Вамаi парний степiнь;

3. множину ребер графа Ваможна розбити на простi цикли.

Доведення.

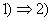Нехай 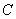- ойлерiв цикл графа . Будемо рухатись по циклу 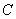. Проходження кожноi вершини збiльшуi степiнь кожноi вершини на 2, i оскiльки кожне ребро входить в 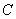Варiвно раз , то будь-яка вершина маi парний степiнь .

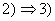Оскiльки 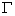Ва- звтАЩязний граф , степiнь кожноi вершини дорiвнюi принаймнi 2; тому в силу леми 2.1 мiстить простий цикл 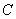. Виключимо ребра циклу 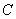, отримаiмо остовний пiдграф 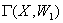, в якому кожна вершина маi парний степiнь. Якщо 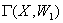Ванемаi ребер , то (3) доведено. В протилеж-ному випадку застосуiмо проведенi вище мiркування до 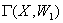, отримаiмо граф 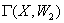, в якому степенi всiх вершин i парними i так далi. Одночасно з порожнiм графом 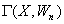Ва, 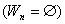Ваотримаiмо розбиття множини ребер на 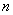Вациклiв

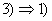ВаНехай множину ребер можна розбити на простi цикли. Нехай 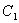ВатАУ один з простих циклiв. Якщо складаiться тiльки з цього циклу , то -ойлерiв граф. В протилежному випадку iснуi iнший простий цикл, який маi вершину 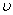Ва, спiльну з 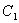. Ланцюг, який розпочинаiться з 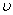Ваi складаiться з циклу 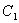Ваi наступного за ним циклу 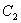, i замкненим ланцюгом, який мiстить всi ребра графа , кожне один раз . Отже , - ойлерiв граф.

З теореми 2.1 випливаi наступна теорема.

Теорема 2.2. ЗвтАЩязний граф i ойлеровим тодi i тiльки тодi, коли кожна його вершина маi парний степiнь.

.

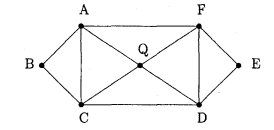
Рис.2.6. Приклад ойлерового графу в теоремi 2.2

Доведення. Граф зображений на рисунку 2.6. i ойлеровим, оскiльки

1. Степiнь вершин А, F, D, C, Q = 4(парнi);

2. Степiнь вершин B, E = 2(парнi);

3. Множина ребер цього графа i обтАЩ iднання двох простих циклiв

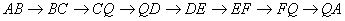Ваi .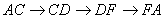

Теорема 2.3. ЗвтАЩязний граф i напiвойлеровим тодi i тiльки тодi , коли в ньому не бiльше двох вершин непарного степеня.

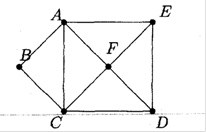
Рис. 2.7. Приклад напiвойлерового графу до теореми 2.3

Доведення. Граф зображений на рисунку 2.7. i нпiвойлеровим, оскiльки

1. Степiнь вершин А, F, C = 4(парнi);

2. Степiнь вершин B = 2(парна);

3. Степiнь вершин E,D = 3(непарна);

4. Ось один з можливих варiантiв обходу 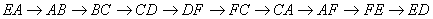. Початковою точкою маршрута i точка 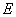, а кiнцевою i точка .

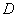Якщо граф маi двi вершини з непарними степенями (див.рис.2.7), то для будь-якого напiойлерового ланцюга одна з цих вершин буде початковою, а дру-га кiнцевою. Для доведення досить сполучити вiдрiзком вершини з непарними степенями.

Зауважимо , що згiдно з Вллемою про рукостисканняВ» - число вершин непарного степеня i парним.

Спробуiмо для довiльного графа вказати найменше число ланцюгiв та-ких, що жоднi два не мають спiльних ребер i всi вони повнiстю накривають ра-зом весь граф. Очевидно, якщо на графi i таке сiмейство ланцюгiв , то кожна вершина непарного степеня повинна бути або початковою, або кiнцевою вер-шиною якогось ланцюга. Загальне число вершин з непарним степенем згiдно з лемою про рукостискання i парним, скажiмо рiвним . Таким чином, кожне сiмейство ланцюгiв, якi накривають граф , повинно мiстити принаймнi 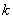Валан-цюгiв.

Доведемо, що iснування Вавершин з непарним степенем i i достатньою умовою iснування ланцюгiв, якi накривають граф.

Теорема 2.4. На будь-якому звтАЩязному графi з Вавершинами непарного степеня iснуi сiмейство ланцюгiв, якi в сукупностi мiстять всi ребра графа в точностi один раз кожне.

Доведення. Позначимо вершини з непарними степенями

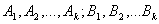
Якщо ми додамо до нашого графу ребра

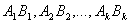
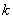то всi вершини отриманого графа будуть парними i на ньому знайдеться ойле-рiв цикл . При вiдкиданнi доданих ребер цикл Варозпадеться на Ваокремих ланцюгiв , якi мiстять всi ребра графа.

Граф , зображений на рисунку 2.8 маi чотири вершини з непарним степе-нем 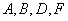Ваi накриваiться двома ланцюгами 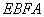Ваi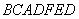

Рис.2.8. Граф з непарним степенем вершин до теореми 2.4

В розважальнiй математицi ось уже впродовж декiлькох столiть розгляд-даються задачi, якi можна сформулювати як задачу пошуку певних маршрутiв в графах, зокрема, пошуку ойлерових циклiв.

Так, граф на рисунку 2.9. називаiться Влшаблею МагометаВ», а ойлерiв цикл необхiдно побудувати за маршрутом, не вiдриваючи пера ручки вiд рисунку за одним разом ( тобто розчерком), викреслити фiгуру, подану на рис.2.9.

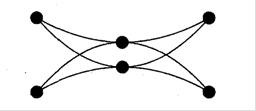
Рис. 2.9. Ойлерiв цикл в графi тАУ ВлШабля МагометаВ»

Бiльшiсть збiрникiв математичних задач з розважальноi математики мiстять задачi про лабiринти. Лабiринт складаiться з коридорiв та iх перех-ресть. Отже , вiн може бути зображений графом, в якому ребра вiдповiдають коридорам, а вершини тАУ перехрестям.

Ойлеровим графом повинен бути i план огляду будь-якоi виставки, i вздовж примiщень виставки потрiбно розставити покажчики обходу таким шля-хом, щоб кожен експонат був оглянутий рiвно один раз.

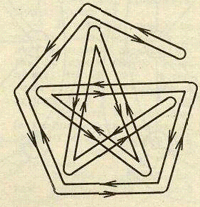
Рис.2.10. Застосування апарату ойлерових циклiв при розвтАЩязаннi задач тАЬмаршрут виставкиВ» [3]

Припустимо, що експонати розташованi з обох сторiн шляху, який про-ходить територiiю виставки. Виявляiться, що тодi, яким би не був вiдповiдний граф ( або лишень вiн був звтАЩязний), можна провести вiдвiдувача так, щоб кож-ний шлях був пройдений двiчi - по одному разу в кожному напрямi (див.рис.2.10).

Теорема 2.5. В звтАЩязному графi iснуi орiiнтований цикл, який проходить через ребро по одному разу в кожному з двох напрямiв.

Доведення.

Сформулюiмо загальне правило побудови ланцюга, який проходить взовж всiх ребер графа в точностi по одному разу в кожному напрямi. Розпоч-немо з довiльноi вершини 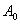Ваi пройдемо вздовж 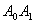, вiдзначивши це ребро маленькою стрiлкою в точцi 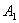, яка показуi вибраний напрям. Потiм перехо-димо послiдовно до iнших вершин. Однiй й тi ж вершини можна вiдвiдувати i декiлька раз. Кожного разу , потрапивши в якусь вершину, ми будемо ставити на вiдповiдному ребрi стрiлку, яка вказуi напрям прибуття. Крiм того, потрап-ляючи в якусь вершину вперше, ми як-небудь вiдзначимо вхiдне ребро, щоб потiм його можна було вiдрiзнити вiд iнших.