Логiка i множини

Мiнiстерство освiти i науки Украiни

Реферат

на тему "Логiка i множини"

з дисциплiни "Дискретна математика"

Харкiв 2011

Змiст

Вступ

1. Логiчнi операцii над пропозицiями

2. Таблиця iстинностi

3. Тавтологiя i логiчна еквiвалентнiсть

4. Функцii висловлювань i множини

5.Функцii множин

6. Логiка квантифiкаторiв

Лiтература

Вступ

Пропозицiя це виcлiв (твердження), який може бути iстинним або хибним тАУ третього не дано. В цьому полягаi один iз фундаментальних принципiв логiки тАУ принцип виключення третього. РЖстиннiсть i хибнiсть називаються логiчними значеннями пропозицii. Пропозицiя "2 + 2 = 4" iстинна, а "p i рацiональне число" хибна. З точки зору граматики пропозицiя i речення тАУ закiнчена думка. Будемо розрiзняти елементарнi пропозицii i складнi. Елементарнiй пропозицii вiдповiдаi просте речення з простими пiдметом i присудком. Виясняти, який з окремих елементарних висловiв i iстинним чи хибним, не i завданням логiки. Логiка займаiться знаходженням логiчних значень складних пропозицiй при умовi, що логiчнi значення складових елементарних пропозицiй вiдомi. РЖснуi багато тверджень, iстиннiсть або хибнiсть яких нiкому не вдаiться довести. Наприклад, вiдома теорема Гольдбаха що "кожне парне число бiльше 2 i сумою двох простих чисел". В даному вище означеннi пропозицii i великий дефект, згiдно нього не завжди можна визначити, чи i дане твердження пропозицiiю. Наприклад, вираз "Я завжди говорю неправду". Тому iнколи замiсть замiсть термiну "пропозицiя" вживають бiльш нейтральний термiн "вислiв", в цьому разi не обовтАЩязково треба знати, iстинний вислiв чи хибний.

1. Логiчнi операцii над пропозицiями

Спочатку зтАЩясуiмо правила зтАЩiднання висловiв для одержання нових висловiв. Позначимо довiльнi вислови p i q.

Означення 1. (КонтАЩюнкцiя) Говорять, що вислiв p∧q (p i q) iстинний, якщо обидва вислови p, q iстиннi i хибний в противному випадку.

Приклад 1. Вислiв "2 + 2 = 4" i "2 + 3 = 5" i iстинним.

Приклад 2. Вислiв "2 + 2 = 4" i "p i число рацiональне" хибний.

Означення 2. (ДизтАЩюнкцiя). Говорять, що вислiв p ∨ q (p або q) хибний, якщо хоча б один з висловiв p, q iстинний, i хибний в противному випадку.

Приклад 3. Вислiв "2 + 2 = 2" або "1 + 3 = 5" хибний.

Приклад 4. Вислiв "2 + 2 = 4" або "p i число рацiональне" iстинний.

Означення 3. (Заперечення) Говоримо, що Ваp (не p) iстинний, якщо p хибний, i навпаки, хибний, якщо p iстинний.

Зауваження. В деяких пiдручниках замiстьВа p вживають позначення , в залежностi вiд зручностi ми будемо користуватися обома.

Приклад 5. Заперечення вислову "2 + 2 = 4" i вислiв "2 + 2 ¹ 4".

Приклад 6. Заперечення вислову "p i число рацiональне" i вислiв "p i число iррацiональне". Означення 4. (РЖмплiкацiя). Говорять, що вислiв p → q (якщо p, то q) iстинний, якщо p хибний, або q iстинний, або обидва iстиннi i хибний в противному випадку. Зауваження. Простiше визначити вислiв p → q як хибний у випадку, коли p iстинний, а q хибний. Це треба розумiти наступним чином. Якщо ми зробили хибний висновок з iстинного, то наше мiркування помилкове. Але допускаiмо, що iстинний висновок може бути одержаний i з хибного припущення.

Приклад 7. Вислiв "якщо 2 + 2 = 2", то "1 + 3 = 5" iстинний, тому що вислiв "2 + 2 = 2" хибний.

Приклад 8. Вислiв "якщо 2 + 2 = 4", то "p i число рацiональне " хибний.

Приклад 9. Вислiв "якщо p i число рацiональне" , то "2 + 2 = 4" iстинний.

Означення 5. (Еквiвалентнiсть) Говорять, що вислiв p Вл q (p тодi i лише тодi, коли q) iстинний у випадку, коли p, q iстиннi або хибнi одночасно i хибний в противному випадку.

Приклад 10. Вислiв "2 + 2 = 4" тодi i лише тодi, коли "p i число рацiональне " iстинний.

Приклад 11. Вислiв "2 + 2 ¹ 4" тодi i лише тодi, коли "p i число рацiональне " також iстинний.

2. Таблиця iстинностi

Якщо вжити Т "true" для позначення iстинного вислову i F "false" для хибного, вище наведенi означення можуть бути представленi у виглядi таблицi iстинностi "truth table":

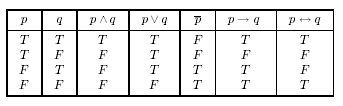
Приклад 1 Побудуiмо таблицю iстинностi для бiльш складноi логiчноi конструкцii

3. Тавтологiя i логiчна еквiвалентнiсть

Означення 1. Тавтологiя це iстинний в логiчному значеннi вислiв.

Важко привести приклад елементарноi пропозицii, яку б можна було назвати тавтологiiю. Як правило це поняття характерне для складних пропозицiй i означаi, якi б не були логiчнi значення складових пропозицiй, складна пропозицiя завжди буде iстинною, якщо вона i тавтологiiю. Всi можливi комбiнацii логiчних значень складових називаються iнтерпретацiями. Вище наведенi таблицi iстинностi показують, що для двох складових iснуi всього 4 iнтерпретацii. Якщо трохи подумати, то прийдемо до висновку, що три складовi мають 23 = 8 iнтерпретацiй i взагалi, n складових мають 2n iнтерпретацiй. Використовуючи цей термiн можна перефразувати означення 1.1 як : тавтологiя тАУ це пропозицiя iстинна при всiх iнтерпретацiях ii складових. Керуючись цим означенням легко довести iстиннiсть наступних пропозицiй:

Приклад 1. Вислови

i тавтологii. Це даi можливiсть писати p ∧ q ∧ r без дужок, узагальнивши поняття контАЩюнкцii для бiльше нiж двох висловiв.

Приклад 2. Вислови

i тавтологii. Це даi можливiсть писати p Ú q Ú r без дужок, узагальнивши поняття дизтАЩюнкцii для бiльше нiж двох висловiв.

Приклад 3. Вислiв p ∨ p i тавтологiя.

Приклад 4. Вислiв (p → q) Вл (q → p) i тавтологiя.

Приклад 5. Вислiв (p → q) Вл (p ∨ q) i тавтологiя.

Приклад 6. Вислiв (p Вл q) Вл ((p∨q)∧(p ∧ q)) i тавтологiя; про що свiдчить наступна таблиця iстинностi:

Пропонуiмо студентам довести, що наступнi вислови i тавтологii.

Розподiльний закон.

(a) (p ∧ (q ∨ r)) Вл ((p ∧ q) ∨ (p ∧ r)); (b) (p ∨ (q ∧ r)) Вл ((p ∨ q) ∧ (p ∨ r)).

Закон де Моргана.

(a) (p ∧ q) Вл (p ∨ q); (b) (p ∨ q) Вл (p ∧ q).

Правила виводу.

(a) (MODUS PONENS) (p ∧ (p → q)) → q;

(b) (MODUS TOLLENS) ((p → q) ∧ q) → p;

Всi цi закони з точки зору логiки i тавтологii, що можна легко довести за допомогою таблицi iстинностi.

Означення 1. Говорять, що вислови p i q логiчно еквiвалентнi, якщо вислiв p Вл q i тавтологiя.

Приклад 7. Вислови p → q i q → p логiчно еквiвалентнi. Останнiй вислiв називають контра позицiiю першого.

Зауваження. Вислови p → q i q → p не i логiчно еквiвалентними. Останнiй називаiться обернений до першого.

4. Функцii висловлювань i множини

В багатьох випадках ми вживаiмо вислови типу "x i парне число", що мiстять одну або декiлька змiнних. Ми будемо називати iх функцiями висловлювань або пропозицiй. В наведеному прикладi вислiв i iстинний для одних значень х i хибний для iнших. Виникають наступнi питання:

Якi значення x допустимi?

Чи вислiв i iстинним при всiх допустимих значеннях x ?

При яких саме допустимих значеннях x вислiв i iстинним?

Щоб вiдповiсти на цi питання нам потрiбно поняття множини. Нехай Р i множина i х i елемент цiii множини. Цей факт позначають x ∈ P. Елементи множини можна задати двома способами:

В· Перечисленням, наприклад {1, 2, 3} означаi множину, що складаiться з чисел 1, 2, 3 i нiчого бiльше;

В· Визначенням властивостi (функцii висловлювань p(x)). В цьому випадку важливо визначити множину U допустимих значень x . Тодi можемо написати

P = {x : x ∈ U i p(x) iстинно} або, просто , P = {x : p(x)}.

Множина без жодного елемента називаiться пустою i позначаiться Æ.

N = {1, 2, 3, 4, 5, ..} називаiться множиною натуральних чисел.

Z = {. . . ,-2,-1, 0, 1, 2, . . .} називаiться множиною цiлих чисел.

{x : x ∈ N i -2 < x < 2} = {1}.

{x : x ∈ Z i -2 < x < 2} = {-1, 0, 1}.

{x : x ∈ N i -1 < x < 1} = Æ.

5. Функцii множин

Припустимо, що функцii висловiв p(x), q(x) вiдносяться до множин P, Q, тобто P = {x : p(x)} i Q = {x : q(x)}. Визначимо наступнi операцii над множинами перетин P ∩ Q = {x : p(x) ∧ q(x)};

обтАЩiднання P ∪ Q = {x : p(x) ∨ q(x)};

доповнення CP = {x : p(x)};

рiзницю P \ Q = {x : p(x) ∧ q(x)}.

Цi означення легко перефразувати у форму

P ∩ Q = {x : x ∈ P i x ∈ Q};

P ∪ Q = {x : x ∈ P або x ∈ Q};

СP = {x : x Ï P};

P \ Q = {x : x ∈ P i x Ï Q}.

Множина P i пiдмножиною Q i позначаiться P ⊆ Q або Q ⊇ P, якщо кожен елемент P i елементом Q. РЖншими словами, для множин P = {x : p(x)} i Q = {x : q(x)} маiмо P ⊆ Q тодi i тiльки тодi, коли p(x) → q(x) для всiх допустимих значень x ∈ U.

Множини P i Q називаються рiвними P = Q якщо вони мiстять тi ж самi елементи, iншими словами, якщо P ⊆ Q i Q ⊆ P.

Множина P називаiться власною пiдмножиною Q i позначаiться P ⊂ Q або Q ⊃ P, якщо P ⊆ Q i P ¹ Q.

Наступнi властивостi функцiй множин можуть бути легко доведенi на основi iх аналогiв в логiцi.

Розподiльний закон. Якщо P,Q,R i множини, то

(a) P ∩ (Q ∪ R) = (P ∩ Q) ∪ (P ∩ R);

(b) P ∪ (Q ∩ R) = (P ∪ Q) ∩ (P ∪ R).

логiка тавтологiя еквiвалентнiсть квантифiкатор

Закон де Моргана. Якщо P,Q i множини, то

(a) С (P ∩ Q) = СP∪ СQ;

(b) С(P ∪ Q) = СP ∩ СQ.

Зробимо це, наприклад, для першого розподiльного закону. Припустимо, що функцii p(x), q(x), r(x) вiдносяться до множин P, Q, R , тобто P = {x : p(x)}, Q = {x : q(x)} i R = {x : r(x)}. Тодi

P ∩ (Q ∪ R) = {x : p(x) ∧ (q(x) ∨ r(x))}

(P ∩ Q) ∪ (P ∩ R) = {x : (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x))}.

Припустимо, що x ∈ P ∩ (Q ∪ R). Тодi p(x) ∧ (q(x) ∨ r(x)) iстинно. По першому розподiльному закону для логiчних функцiй маiмо тавтологiю

(p(x) ∧ (q(x) ∨ r(x))) Вл ((p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)))

Звiдси слiдуi, що (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)) iстинно, так що x ∈ (P ∩ Q) ∪ (P ∩ R). А це значить, що

(1) P ∩ (Q ∪ R) ⊆ (P ∩ Q) ∪ (P ∩ R).

Тепер припустимо, що x ∈ (P ∩ Q) ∪ (P ∩ R). Тодi (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)) iстинно. З першого розподiльного закону для логiчних функцiй слiдуi, що p(x) ∧ (q(x) ∨ r(x)) iстинно, так що x ∈ P ∩ (Q ∪ R). Це даi

(2) (P ∩ Q) ∪ (P ∩ R) ⊆ P ∩ (Q ∪ R).

Потрiбний результат слiдуi з (1) i (2).

6. Логiка квантифiкаторiв

Повернемось до прикладу "x i парне число". Обмежимо x множиною цiлих чисел Z . Tодi вислiв "x i парне число" iстинний лише для деяких x в Z. Звiдси слiдуi, що вислiв "деякi x ∈ Z парнi" iстинний, якщо вислiв "всi x ∈ Z непарнi" хибний.

В загальному випадку розглянемо функцiю вислiв p(x) в якiй змiнна x належить певнiй множинi. Введемо наступнi позначення для висловiв

∀x, p(x) (для всiх x, p(x) iстинний);

∃x, p(x) (для деяких x, p(x) iстинний).

Символ ∀ (для всiх) i ∃ (для деяких) називаються вiдповiдно унiверсальним квантифiкатором i квантифiкатором iснування. Зауважимо, що змiнна x не i суттiва, вона може бути замiнена будь якою iншою, так що ∀x, p(x) i ∀y, p(y) означають одне й те ж саме.

(Теорема Лагранжа) Кожне натуральне число i сума квадратiв чотирьох цiлих чисел. Це можна записати як

∀n ∈ N, ∃a, b, c, d ∈ Z, n = a2 + b2 + c2 + d2.

(Гiпотеза Гольдбаха) Кожне парне число бiльше 2 i сума двох простих чисел. Це можна записати як

∀n ∈ N \ {1}, ∃p, q простi, 2n = p + q.

Ще невiдомо, чи це дiйсно так. Це одна з найцiкавiших з ще не розвтАЩязаних проблем математики.

Заперечення

Розглянемо заперечення висловiв з квантифiкаторами. Давайте скажемо, що всi люди дурнi. Дехто з вас з цим не погодиться. Можна здогадатися, що запереченням вислову ∀x, p(x) буде вислiв ∃x, p(x). Тепер будемо не так категоричними i скажемо, що дехто з вас дурень. Якщо i цього разу заперечите, то запереченням вислову ∃x, p(x) буде ∀x, p(x). Отже, маiмо формули аналогiчнi законам де Моргана для квантiфiкаторiв

∀x, p(x) Вл ∃x, p(x)

∃x, p(x) Вл ∀x, p(x).

Пiдсумовуючи сказане, заперечуючи вислiв з кавантифiкатрором ми змiнюiмо квантифiкатор i заперечуiмо функцiю висловiв. Застосовуючи це правило послiдовно декiлька раз одержимо заперечення бiльш складного вислову

спочатку як

Потiм

i, нарештi,

Запереченням гiпотези Гольдбаха в термiнах квантифiкаторiв буде

∃n ∈ N \ {1}, ∀p, q простi числа, 2n ¹ p + q.

РЖншими словами, iснуi парне число бiльше 2, яке не i сумою двох простих чисел. Отже, щоб вiдкинути гiпотезу Гольдбаха досить знайти таке число. Це називаiться "привести контр приклад".

Лiтература

1. Вища математика: Основнi означення, приклади i задачi. У 2-х кн. / За ред. РЖ.П.Васильченко. _ К: Либiдь, 1994.- 280 ст.

2. Шкiль М.РЖ. Вища математика: Пiдручник у 3-х кн./ Шкiль М.РЖ., Колеснiк Т.В., Котлова В.М. тАУ К.: Либiдь, 1994.

3. Вища математика: Основнi означення, приклади i задачi. У 2-х кн. / За ред. Г.Л. Кулiнiча: Пiдручник К.: Либiдь, 1994.

4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, 1985.

5. Карасев А.И., Аксютина Э.М., Савельева Т.И. Курс высшей математики для экономических вузов. М.: Высшая школа. ч. 1,2. 1990.

6. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, 1988, т.1,2.

7. Ильин В.Н., Позняк З.Г. Аналитическая геометрия. М. :Наука, 1984.

8. Ильин В.Н., Позняк З.Г. Линейная алгебра. М.: Наука, 1989.

9. Бахвалов С.В. Аналитическая геометрия. - М.: Высшая школа, 1992.

10. Цубербиллер О.Н. Задачи по аналитической геометрии. М.: Высшая школа, 1984.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики