Числовi характеристики системи випадкових величин та iх граничнi теореми
Числовi характеристики системи випадкових величин та iх граничнi теореми
1. Кореляцiйний момент, коефiцiiнт кореляцii
Кореляцiйним моментом (коварiацiiю) випадкових величин ![]() Ваi
Ваi ![]() Ваназиваiться математичне сподiвання добутку вiдповiдних ним центрованих величин:
Ваназиваiться математичне сподiвання добутку вiдповiдних ним центрованих величин:
![]() Ва. (1)
Ва. (1)
Властивостi коварiацii:
1. | ||
2. | ||
3. |
Першi двi з них очевиднi, остання доводиться також легко:
![]()
Коефiцiiнтом кореляцii називаiться кореляцiйний момент нормованоi випадковоi величини:
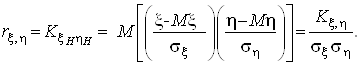
Теорема. Для будь-яких випадкових величин ![]() ,
, ![]() Вакоефiцiiнт кореляцii
Вакоефiцiiнт кореляцii ![]() Вапричому знак рiвностi можливий тодi i тiльки тодi, коли
Вапричому знак рiвностi можливий тодi i тiльки тодi, коли ![]() Ваi
Ваi ![]() Ваз iмовiрнiстю 1 пов'язанi лiнiйно.
Ваз iмовiрнiстю 1 пов'язанi лiнiйно.
Доведення. Обчислимо дисперсiю лiнiйноi комбiнацii випадкових величин ![]() Ваi
Ваi ![]() Ваз довiльним коефiцiiнтом
Ваз довiльним коефiцiiнтом ![]() Вата врахуiмо, що з властивостей дисперсii вона i невiд'iмною.
Вата врахуiмо, що з властивостей дисперсii вона i невiд'iмною.
При цьому отримаiмо невiдтАЩiмну квадратичну форму вiдносно змiнноi ![]() Ваз невiдтАЩiмним коефiцiiнтом при
Ваз невiдтАЩiмним коефiцiiнтом при ![]() .
.
![]()
Це можливо лише за умови, що ii дискримiнант ![]() . З урахуванням визначення (1) цю нерiвнiсть можна переписати у виглядi:
. З урахуванням визначення (1) цю нерiвнiсть можна переписати у виглядi:
![]()
або
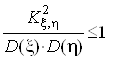
або мовою середнiх квадратичних вiдхилень випадкових величин
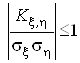 .
.
Тобто
![]()
Доведемо тепер другу частину теореми: ![]() Ватодi i тiльки тодi, коли
Ватодi i тiльки тодi, коли ![]() Ваi
Ваi ![]() Ваз iмовiрнiстю 1 пов'язанi лiнiйно.
Ваз iмовiрнiстю 1 пов'язанi лiнiйно.
Необхiднiсть:
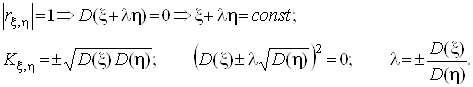
Достатнiсть:
![]() ,
,  ,
, ![]() ,
,
![]() ,
, 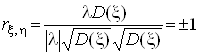 .
.
Випадковi величини x,h називаються некорельованими, якщо iх коварiацiя дорiвнюi нулю. Якщо випадковi величини x, h незалежнi, то вони некорельованi.
![]() .
.
Зворотне твердження, взагалi кажучи, не маi мiсця.
Наприклад,
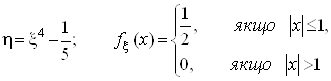 .
.
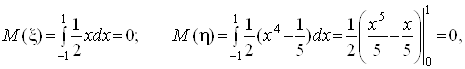
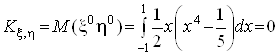 .
.
Для опису зв'язкiв, що iснують мiж проекцiями випадкового вектора (x,h), крiм коварiацii ![]() Ваможна використовувати числовi характеристики умовних законiв розподiлу
Ваможна використовувати числовi характеристики умовних законiв розподiлу ![]() ,
, ![]() .
.
Умовним середнiм значенням ![]() Ваi умовною дисперсiiю
Ваi умовною дисперсiiю ![]() Вавипадковоi величини x за умови h =y називаються величини:
Вавипадковоi величини x за умови h =y називаються величини:
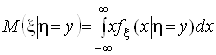 ,
,
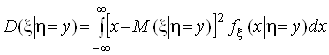 .
.
Аналогiчно визначаються характеристики ![]() Ваi
Ваi ![]() .
.
Для опису випадкового вектора також вводять початковi i центральнi моменти:
![]() ,
, ![]() .
.
2. Комплексна випадкова величина, характеристичнi функцii
Комплексна випадкова величина, що вводиться за формулою ![]() , i iншим способом опису випадкового вектора (
, i iншим способом опису випадкового вектора (![]() ,
,![]() ).
).
Випадковi величини ![]() Ваi
Ваi ![]() Ваназиваються незалежними, якщо незалежними i випадковi вектори (
Ваназиваються незалежними, якщо незалежними i випадковi вектори (![]() ,
,![]() ) i (
) i (![]() ,
,![]() ).
).
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Характеристичною функцiiю випадковоi величини ![]() Ваназиваiться середнi значення виразу
Ваназиваiться середнi значення виразу ![]() .
.
![]() .
.
Функцiю ![]() Ваназивають також характеристичною функцiiю вiдповiдного закону розподiлу:
Ваназивають також характеристичною функцiiю вiдповiдного закону розподiлу:
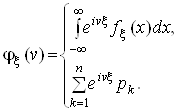 Ва(2)
Ва(2)
Як видно з (2), характеристична функцiя ![]() Ваi перетворенням Фур'i вiдповiдноi iй щiльностi iмовiрностi:
Ваi перетворенням Фур'i вiдповiдноi iй щiльностi iмовiрностi:
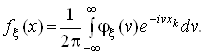
Властивiсть 1. При додаваннi незалежних випадкових величин iхнi характеристичнi функцii перемножуються.

Властивiсть 2. Розкладання характеристичноi функцii в ряд за ступенями ![]() Вадозволяi знайти всi моменти
Вадозволяi знайти всi моменти ![]() ,
, ![]() ,
, ![]() ,тАжвипадковоi величини
,тАжвипадковоi величини ![]() .
.

3. Види збiжностi випадкових величин
Послiдовнiсть випадкових величин x1, x2тАжназиваiться такою, що збiгаiться з випадковою величиною x в розумiннi середнього квадратичного, якщо границя математичного сподiвання квадрата абсолютного значення вiдхилення ![]() Вавiд
Вавiд ![]() Вапрямуi до нуля за умови, що
Вапрямуi до нуля за умови, що ![]() , тобто
, тобто
![]() .
.
Величина x називаiться ще СК границею послiдовностi {xn}.
![]() Вачи
Вачи ![]() .
.
Оскiльки
![]() ,
,
СК збiжнiсть рiвносильна виконанню умов:
![]() .
.
Послiдовнiсть випадкових величин ![]() Вазбiгаiться з випадковою величиною
Вазбiгаiться з випадковою величиною ![]() Вапри
Вапри ![]() Ваза iмовiрнiстю, якщо для кожного будь-якого e>0
Ваза iмовiрнiстю, якщо для кожного будь-якого e>0
![]() ,
,
![]() .
.
Збiжнiсть послiдовностi ![]() Вадо випадковоi величини
Вадо випадковоi величини ![]() Ваза ймовiрнiстю символiчно позначаiться таким чином:
Ваза ймовiрнiстю символiчно позначаiться таким чином:
![]() .
.
Для будь-якоi випадковоi величини ![]() Вапри будь-якому e>0
Вапри будь-якому e>0
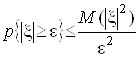 .
.
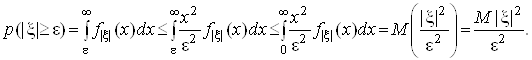
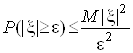 .
.
Наслiдок.
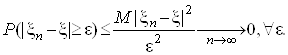
Зi збiжностi у СК випливаi збiжнiсть за ймовiрнiстю.
4. Граничнi теореми теорii ймовiрностей
Нерiвнiсть Чебишева.
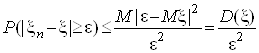 .
.
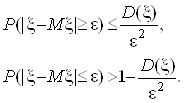 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
Як випливаi з нерiвностей (3) зi зменшенням дисперсii ![]() , основна частина площi пiд кривоi fx(x) виявляiться зосередженою в околi точки
, основна частина площi пiд кривоi fx(x) виявляiться зосередженою в околi точки ![]() .
.
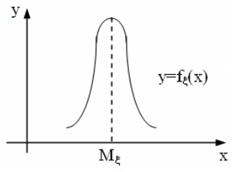
Рисунок 1
Внаслiдок своii загальностi нерiвнiсть Чебишева даi дуже грубу оцiнку ймовiрностi, що входить до неi.
Наприклад, 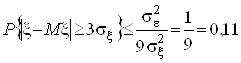 .
.
![]() , якщо
, якщо ![]() .
.
Вважають, що послiдовнiсть функцiй розподiлу ![]() ,
, ![]() ,
, ![]() ,..,
,.., ![]() ,.. збiгаiться до функцii розподiлу
,.. збiгаiться до функцii розподiлу ![]() , якщо
, якщо
![]()
в усiх точках неперервностi.
Якщо ![]() , то
, то ![]() .
.
Практичне використання теорii ймовiрностей засновано на такому принципi: випадкову подiю, ймовiрнiсть якоi досить близька до 1, можна вважати достовiрною та неможливою при дуже малiй ймовiрностi.
Теореми, що забезпечують виконання такоi схеми обробки даних, називаються законами великих чисел.
Теорема Чебишева
Нехай h1, h2тАжтАУпослiдовнiсть попарно незалежних випадкових величин, дисперсii яких обмеженi
![]() , k=1,2 тАж
, k=1,2 тАж
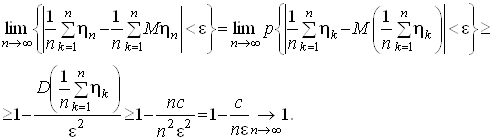
Тодi при будь-якому e>0
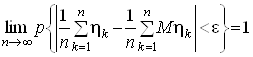 .
.
Теорема Бернуллi.
Нехай xn тАУ число появ деякоi подii А в серii з n незалежних iспитiв, р тАУ ймовiрнiсть появи А в окремому iспитi.
Тодi
![]()
тобто для кожного e>0
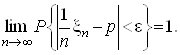
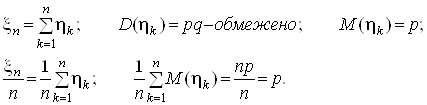
Застосовуючи теорему Чебишева, одержимо формулу, що очiкуiмо при необмеженiй кiлькостi випробувань.
![]() Вор.
Вор.
Збiг теоретичних розрахункiв iз закономiрностями, що фактично спостерiгаються, свiдчить про правильну схему побудови теорii ймовiрностей. збiжнiсть випадковий величина ймовiрнiсть
Центральна гранична теорема.
Нехай x1,x2,тАжпослiдовнiсть незалежних випадкових величин, що мають дисперсiю D1,D2,тАжDnтАжТретi абсолютнi центральнi моменти iх обмеженi mk=M|xk-Mxk|3£C.
Тодi випадкова величина
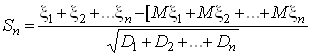
розподiлена асимптотично нормально iз середнiм ![]() Ваi
Ваi ![]() , тобто
, тобто
Р(a
при nВо¥.
Теорема Муавра-Лапласса (окремий випадок).
Нехай xn тАУ число появ деякоi подii А у серii з n незалежних випробувань, р тАУ ймовiрнiсть появи подii А в окремому випробуваннi. Тодi
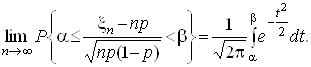
Теорема дозволяi при досить великих n одержати ймовiрнiсть:

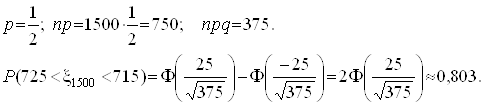
Приклад 1. Обчислити ймовiрнiсть Р(715
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики