Решение задач по высшей математике

КОНТРОЛЬНАЯ РАБОТА

Решение задач по высшей математике

Задача 1

Вычислить определители:

;

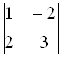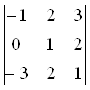Решение

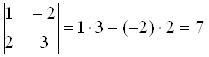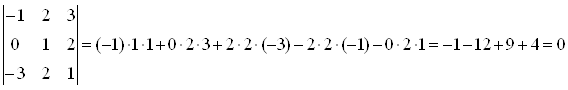
Задача 2

Вычислить определитель:

Решение

Используя теорему Лапласа, разложим определитель по элементам третьего столбца

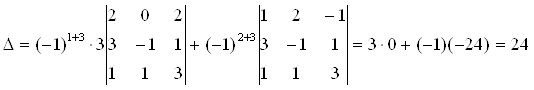Задача 3

Найти матрицу, обратную к матрице .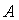

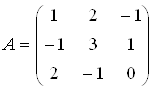
Решение

Находим определитель матрицы и все алгебраические дополнения :

;

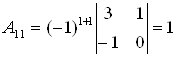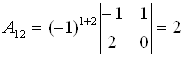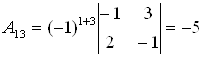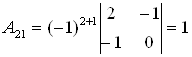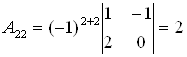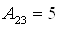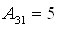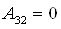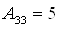Ответ: Обратная матрица имеет вид:

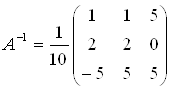Задача 4

С помощью элементарных преобразований вычислить ранг матрицы

Решение

Прибавляя к последней строке учетверенную вторую строку и сокращая затем последнюю строку на , а после этого складывая последний столбец со вторым и третьим последовательно, получим

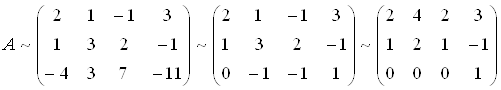Знак ~ обозначает, что матрицы получены одна из другой с помощью элементарных преобразований и их ранги равны. Сокращая второй столбец на два и вычитая первый столбец со всех остальных столбцов, а затем вычитая последнюю строку из первой и меняя местами столбцы, получаем

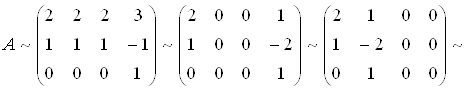
Ответ: Ранг матрицы равен двум.

Задача 5

Решить следующую систему линейных алгебраических уравнений по правилу Крамера:

;

Решение

Вычислим главный определитель системы 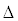Ваи вспомогательные определители , ,.

;

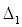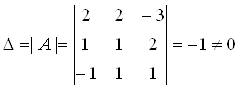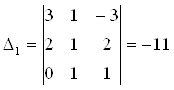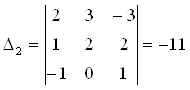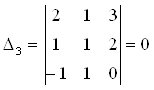По формуле Крамера, получим

;

; .

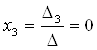Задача 6

Исследовать на совместность систему линейных алгебраических уравнений и, в случае положительного ответа, найти её решение.

Решение

Матрица 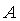Ваи 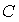Ваимеют вид

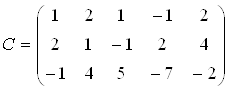Их ранги равны . Система совместна. Выделим следующую подсистему

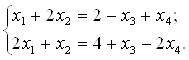
Считая 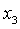Ваи Ваизвестными, решение подсистемы находим по формулам Крамера . Оно имеет вид

; ,

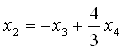где 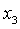, Ва- могут принимать произвольные значения. Пусть 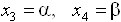Ва, где 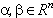ВаТогда ответом будет служить множество

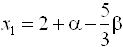
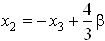
Задача 7

Даны начало 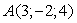Ваи конец Вавектора 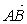. Найти вектор 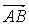Ваи его длину.

Решение

Имеем 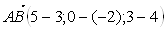, откуда Ваили .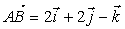

Далее 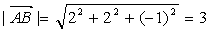, т.е. .

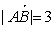Задача 8

Даны вершины треугольника 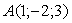, 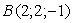Ваи 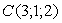. Найти с точность до Ваугол Вапри вершине .

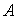Решение

Задача сводится к нахождению угла между векторам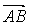и Ваи :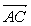

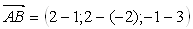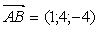, ; . Тогда , .

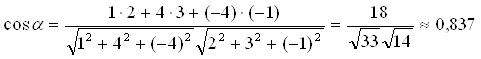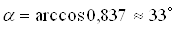Задача 9

Даны вершины треугольника 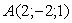, 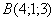Ваи 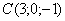. Вычислить площадь этого треугольника.

Решение

Так как площадь треугольника Варавна половине площади параллелограмма, построенного на векторах 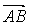Ваи 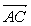как на сторонах, т.е. 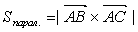, то 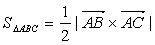. Найдем векторы 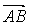Ваи :

; ; .

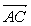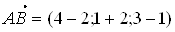Вычислим их векторное произведение:

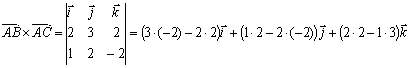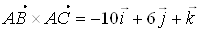Откуда

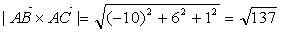. Следовательно, 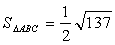Ва(кв. ед.).

Задача 10

Даны вершины треугольной пирамиды 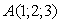, , 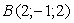Ваи 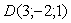. Найти ее объем.

Решение

Имеем 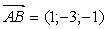, Ваи 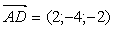. Найдем векторное произведение

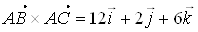Этот вектор скалярно умножим на вектор :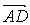

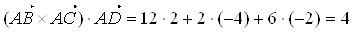Это смешанное произведение можно найти непосредственно по приведенной формуле:

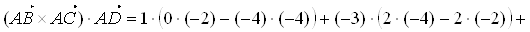
Следовательно, объем:

, Ва(куб. ед.).

Задача 11

Составить уравнение прямой, проходящей через точки 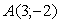Ваи .

Решение

За первую вершину примем 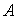Ва(на результат это не влияет); следовательно,

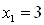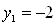Имеем

, , ,

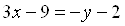Ответ: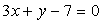Ва- общее уравнение искомой прямой.

Задача 12

Составить уравнение прямой, проходящей через точку , параллельно и перпендикулярно прямой .

Решение

Найдем угловой коэффициент данной прямой: 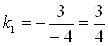. Согласно условиям параллельности и перпендикулярности двух прямых, угловой коэффициент параллельной прямой будет равен 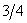, а перпендикулярной прямой будет равен тАУ4 /3. Составляем уравнения искомых прямых:

1) параллельной: 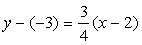, Ва- общее уравнение прямой, параллельной данной;

2) перпендикулярной: 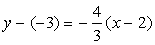, 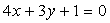Ва- общее уравнение прямой, перпендикулярной к данной.

Задача 13

Найти расстояние между двумя параллельными прямыми 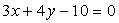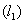Ваи .

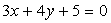
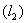Решение

Выберем на одной из данных прямых точку 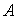. Пусть 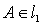. Для определения координат точки 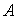Вана прямой 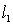Ваодну координату выберем произвольно, а вторую определим из уравнения. Возьмём ; тогда 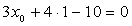, Ваи 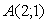. По формуле расстояния от точки до прямой находим:

; .

Задача 14

Исследовать на абсолютную и условную сходимость

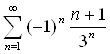Решение

Проверим выполнение условий теоремы Лейбница

а)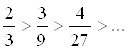

б)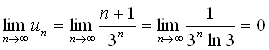

(при вычислении предела применялось правило Лопиталя). Условия выполняются, следовательно, ряд сходится. Исследуем ряд на абсолютную сходимость.

Имеем:

Тогда по признаку Даламбера:

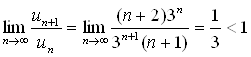, и ряд, составленный из абсолютных величин элементов исходного ряда, будет сходится. Следовательно, ряд 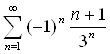Васходится абсолютно.

а)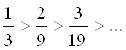

б) ,

следовательно ряд 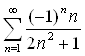Ва- сходится.

2) Пусть 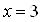. Тогда 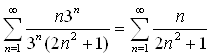. Применим признак сравнения, сравнивая его с расходящимся гармоническим рядом 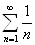. Имеем

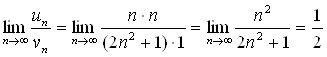Таким образом, ряд 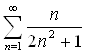Ва- расходится.

Ответ

Область сходимости ряда Ваесть интервал .

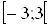Задача 15

Вычислить предел .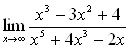

Решение

Для вычисления этого предела непосредственно применить указанные теоремы нельзя, так как пределы функций, находящихся в числителе и знаменателе, не существуют. Здесь имеется неопределенность вида , для раскрытия которой в данном случае следует числитель и знаменатель дроби разделить на наибольшую степень переменной 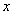, т.е. на :

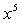так как 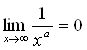Вапри .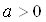

Задача 16

Вычислить придел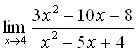

Решение

Так как предел знаменателя равен нулю, то теорема 3 неприменима. Здесь имеется неопределенность вида 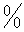. Для раскрытия этой неопределенности в числителе и знаменателе следует выделить бесконечно малый множитель, на который затем сократить дробь. Для этого воспользуемся формулой разложения квадратного трехчлена на множители

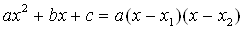, где 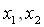Ва- его корни.

Тогда

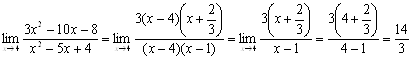Задача 17

Вычислить предел .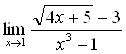

Решение

Умножив числитель и знаменатель на выражение, сопряженное к числителю, получим:

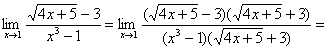
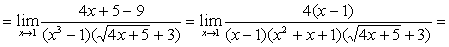
Задача 18

Вычислить предел .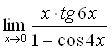

Решение

Легко убедиться, что Ва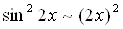и Вапри .

Поэтому

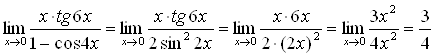Задача 19

Вычислить предел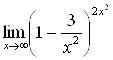

Решение

Для того, чтобы воспользоваться вторым замечательным пределом, в показателе степени выделим величину, обратную второму слагаемому основания и получим

Задача 20

Найти предел .

Решение

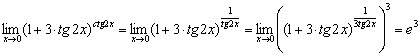Задача 21

Продифференцировать функцию .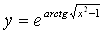

Решение

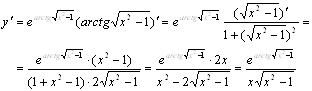Задача 22

Вычислить при помощи дифференциала .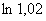

Решение

Пусть . Тогда 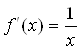. Обозначим: ; . Отсюда 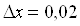. Находим 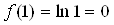Ваи .

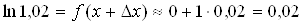Итак, .

Задача 23

Найти .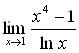

Решение

Подстановка в заданную функцию значения Ваприводит к неопределенности вида 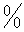. Применив правило Лопиталя, получим:

Задача 24

Исследовать на экстремум функцию

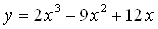Решение

1. Находим область определения функции:.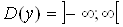

2. Находим производную функции: .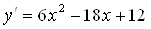

3. Находим критические точки, решая уравнение 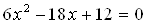Ваили . Критические точки , .

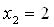4. Область определения функции разбиваем критическими точками Ваи Вана интервалы, в каждом из которых определяем знак , делаем вывод о характере монотонности функции на каждом из интервалов и отмечаем наличие экстремумов.


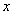
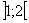
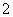
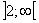
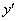
+	0	тАФ	0	+
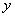
Возрастает	Max	убывает	Min	Возрастает

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики