Незалежнi випробування
Курсова робота
з дисциплини: Теорема ймовiрностi
на тему: Незалежнi випробування
Введення
При практичному застосуваннi теорii ймовiрностей часто доводиться зустрiчатися iз задачами, у яких те саме випробування повторюiться неодноразово. У результатi кожного випробування може з'явитися або не з'явитися деяка подiя А, причому нас не цiкавить результат кожного окремого випробування, а загальне число появ подii А в результатi серii досвiдiв. Наприклад, якщо виробляiться група пострiлiв по однiii й тiй же метi, нас, як правило, не цiкавить результат кожного пострiлу, а загальне число влучень. У подiбних задачах потрiбно вмiти визначати ймовiрнiсть будь-якого заданого числа появ подii в результатi серii досвiдiв. Такi задачi й будуть розглянутi. Вони вирiшуються досить просто у випадку, коли випробування i незалежними.
Визначення. Випробування називаються незалежними, якщо ймовiрнiсть того або iншого результату кожного з випробувань не залежить вiд того, якi результати мали iншi випробування.
Наприклад, кiлька кидань монети являють собою незалежнi випробування.
1. Формула Бернуллi
Нехай зроблено два випробування(n=2). У результатi можливе настання одного з наступних подiй: ![]()
Вiдповiднi ймовiрностi даних подiй такi: ![]() .
.
![]() Ваабо
Ваабо ![]() Ва- настання подii тiльки в одному випробуваннi.
Ва- настання подii тiльки в одному випробуваннi.
![]() Ва- iмовiрнiсть настання подii два рази.
Ва- iмовiрнiсть настання подii два рази.
![]() Ва- iмовiрнiсть настання подii тiльки один раз.
Ва- iмовiрнiсть настання подii тiльки один раз.
![]() Ва- iмовiрнiсть настання подii нуль раз.
Ва- iмовiрнiсть настання подii нуль раз.
Нехай тепер n=3. Тодi можливе настання одного з наступних варiантiв подiй:
![]() .
.
Вiдповiднi ймовiрностi рiвнi ![]() .
.
Очевидно, що отриманi результати при n=2 i n=3 i елементами
![]() и.
и.![]()
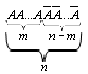
Тепер допустимо, зроблено n випробувань. Подiя А може наступити n раз, 0 разiв, n-1 раз i т.д. Напишемо подiю, що складаiться в настаннi подii А m раз
![]()
Необхiдно знайти число випробувань, у яких подiя А наступить m раз. Для цього треба знайти число комбiнацiй з n елементiв, у яких А повторюiться m раз, а ![]() Ваn-m раз.
Ваn-m раз.
![]()
![]() Ва- iмовiрнiсть настання подii А.
Ва- iмовiрнiсть настання подii А.
![]() (1)
(1)
Остання формула називаiться формулою Бернуллi i являi собою загальний член розкладання ![]() :
:
![]() .
.
З формули (1) видно, що ii зручно використовувати, коли число випробувань не занадто велике.
Приклади
№1. Кидаiться монета 7 разiв. Знайти ймовiрнiсть настання орла три рази.
Рiшення.
n=7, m=3
![]()
![]()
![]() .
.
№2. Щодня акцii корпорацii АВС пiднiмаються в цiнi або падають у цiнi на один пункт iз ймовiрностями вiдповiдно 0,75 i 0,25. Знайти ймовiрнiсть того, що акцii пiсля шести днiв повернуться до своii первiсноi цiни. Прийняти умову, що змiни цiни акцii нагору й долiлиць - незалежнi подii.
Рiшення. Для того, щоб акцii повернулися за 6 днiв до своii первiсноi цiни, потрiбно, щоб за цей час вони 3 рази пiднялися в цiнi й три рази опустилися в цiнi. Шукана ймовiрнiсть розраховуiться по формулi Бернуллi
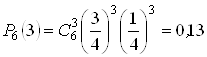
№3. Мотори багатомоторного лiтака виходять iз ладу пiд час польоту незалежно один вiд iншого з iмовiрнiстю р. Багатомоторний лiтак продовжуi летiти, якщо працюi не менш половини його моторiв. При яких значеннях р двомоторний лiтак надiйнiше чотиримоторного лiтака?
Рiшення. Двомоторний лiтак терпить аварiю, якщо вiдмовляють обоi його мотора. Це вiдбуваiться з iмовiрнiстю р2. Чотиримоторний лiтак терпить аварiю, якщо виходять iз ладу всi 4 мотори а це вiдбуваiться з iмовiрнiстю р4, або виходять iз ладу три мотори з 4-х. РЖмовiрнiсть останньоi подii обчислюiться по формулi Бернуллi: ![]() . Щоб двомоторний лiтак був надiйнiше, нiж чотиримоторний, потрiбно, щоб виконувалася нерiвнiсть
. Щоб двомоторний лiтак був надiйнiше, нiж чотиримоторний, потрiбно, щоб виконувалася нерiвнiсть
р2<р4+4p3(1тАУp)
Ця нерiвнiсть зводиться до нерiвностi (3 р-р-1)( р-р-1)<0. Другий спiвмножник у лiвiй частинi цiii нерiвностi завжди негативний (за умовою задачi). Отже, величина 3 р-р-1 повинна бути позитивноi, звiдки треба, що повинне виконуватися умову р>1/3. Слiд зазначити, що якби ймовiрнiсть виходу з ладу мотора лiтака перевищувала одну третину, сама iдея використання авiацii для пасажирських перевезень була б дуже сумнiвною.
№4. Бригада з десяти чоловiк iде обiдати. РД двi однаковi iдальнi, i кожний член бригади незалежно один вiд iншого йде обiдати в кожну iз цих iдалень. Якщо в одну з iдалень випадково прийде бiльше вiдвiдувачiв, чим у нiй i мiсць, то виникаi черга. Яке найменше число мiсць повинне бути в кожнiй з iдалень, щоб iмовiрнiсть виникнення черги була менше 0,15?
Рiшення. Рiшення задачi прийде шукати перебором можливих варiантiв. Спочатку помiтимо, що якщо в кожнiй iдальнi по 10 мiсць, то виникнення черги неможливо. Якщо в кожнiй iдальнi по 9 мiсць, то черга виникне тiльки у випадку, якщо всi 10 вiдвiдувачiв потраплять в одну iдальню. З умови задачi треба, що кожний член бригади вибираi дану iдальню з iмовiрнiстю 1/2. Виходить, усi зберуться в однiй iдальнi з iмовiрнiстю 2(1/2)10=1/512. Це число багато менше, нiж 0,15, i варто провести розрахунок для iдалень. Якщо в кожнiй iдальнi по 8 мiсць, то черга виникне, якщо всi члени бригади прийдуть в одну iдальню, iмовiрнiсть цiii подii вже обчислена, або 9 чоловiк пiдуть в одну iдальню, а 1 чоловiк вибере iншу iдальню. РЖмовiрнiсть цiii подii розраховуiться за допомогою формули Бернуллi ![]() . Таким чином, якщо в iдальнях по 8 мiсць, то черга виникаi з iмовiрнiстю 11/512, що поки ще менше, нiж 0,15. Нехай тепер у кожнiй з iдалень по 7 мiсць. Крiм двох розглянутих варiантiв, у цьому випадку черга виникне, якщо в одну з iдалень прийде 8 чоловiк, а в iншу 2 чоловiк. Це може вiдбутися з iмовiрнiстю
. Таким чином, якщо в iдальнях по 8 мiсць, то черга виникаi з iмовiрнiстю 11/512, що поки ще менше, нiж 0,15. Нехай тепер у кожнiй з iдалень по 7 мiсць. Крiм двох розглянутих варiантiв, у цьому випадку черга виникне, якщо в одну з iдалень прийде 8 чоловiк, а в iншу 2 чоловiк. Це може вiдбутися з iмовiрнiстю ![]() .
.
Виходить, у цьому випадку черга виникаi з iмовiрнiстю 56/512=0,109375<0,15. Дiючи аналогiчним образом, обчислюiмо, що якщо в кожнiй iдальнi 6 мiсць, то черга виникаi з iмовiрнiстю 56/512+120/512=176/512=0,34375. Звiдси одержуiмо, що найменше число мiсць у кожнiй iдальнi повинне рiвнятися семи.
№5. В урнi 20 бiлих i 10 чорних куль. Вийняли 4 кулi, причому кожну вийняту кулю повертають в урну перед добуванням наступнi й кулi в урнi перемiшують. Знайти ймовiрнiсть того, що iз чотирьох вийнятих куль виявиться 2 бiлих.
Рiшення. Подiя А тАУ дiстали бiлу кулю. Тодi ймовiрностi
![]() ,
, ![]() .
.
По формулi Бернуллi необхiдна ймовiрнiсть дорiвнюi
![]() .
.
№6. Визначити ймовiрнiсть того, що в родинi, що маi 5 дiтей, буде не бiльше трьох дiвчинок. РЖмовiрностi народження хлопчика й дiвчинки передбачаються однаковими.
Рiшення. РЖмовiрнiсть народження дiвчинки
![]() , тодi
, тодi ![]() .
.
Знайдемо ймовiрностi того, що в родинi немаi дiвчинок, народилася одна, двi або три дiвчинки:
бернуллi формула лаплас ймовiрнiсть
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Отже, шукана ймовiрнiсть
![]() .
.
№7. Серед деталей, оброблюваних робiтником, буваi в середньому 4% нестандартнi. Знайти ймовiрнiсть того, що серед узятих на випробування 30 деталей двi будуть нестандартними.
Рiшення. Тут досвiд полягаi в перевiрцi кожноi з 30 деталей на якiсть. Подiя А - "поява нестандартноi деталi", його ймовiрнiсть ![]() , тодi
, тодi ![]() . Звiдси по формулi Бернуллi знаходимо
. Звiдси по формулi Бернуллi знаходимо
![]() .
.
№8. При кожному окремому пострiлi зi знаряддя ймовiрнiсть поразки мети дорiвнюi 0,9. Знайти ймовiрнiсть того, що з 20 пострiлiв число вдалих буде не менш 16 i не бiльше 19.
Рiшення. Обчислюiмо по формулi Бернуллi:
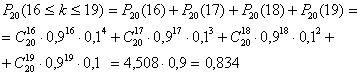
№9. Незалежнi випробування тривають доти, поки подiя А не вiдбудеться k раз. Знайти ймовiрнiсть того, що буде потрiбно n випробувань (n i k), якщо в кожному з них ![]() .
.
Рiшення. Подiя В тАУ рiвно n випробувань до k-го появи подii А тАУ i добуток двох наступних подiй:
D тАУ в n-ом випробуваннi А вiдбулося;
С тАУ у першi (nтАУ1)-ом випробуваннях А з'явилося (до-1) раз.
Теорема множення й формула Бернуллi дають необхiдну ймовiрнiсть:
![]() .
.
№10. З n акумуляторiв за рiк зберiгання k виходить iз ладу. Вибирають m акумуляторiв. Визначити ймовiрнiсть того, що серед них l справних n = 100, k = 7, m = 5, l = 3.
Рiшення: Маiмо схему Бернуллi з параметрами p=7/100=0,07 (iмовiрнiсть того, що акумулятор вийде з ладу), n = 5 (число випробувань), k = 5-3 =2 (число "успiхiв", несправних акумуляторiв). Будемо використовувати формулу Бернуллi (iмовiрнiсть того, що в n випробуваннях подiя вiдбудеться k раз).
![]()
Одержуiмо
![]()
№11. Пристрiй, що складаiться з п'яти незалежно працюючих елементiв, включаiться за час Т. РЖмовiрнiсть вiдмови кожного з них за цей час дорiвнюi 0,2. Знайти ймовiрнiсть того, що вiдмовлять: а) три елементи; б) не менш чотирьох елементiв; в) хоча б один елемент.
Рiшення: Маiмо схему Бернуллi з параметрами p = 0,2 (iмовiрнiсть того, що елемент вiдмовить), n = 5 (число випробувань, тобто число елементiв), k (число "успiхiв", що вiдмовили елементiв). Будемо використовувати формулу Бернуллi (iмовiрнiсть того, що для n елементiв вiдмова вiдбудеться в k елементах): ![]() . Одержуiмо а)
. Одержуiмо а) ![]() Ва- iмовiрнiсть того, що вiдмовлять рiвно три елементи з п'яти. б)
Ва- iмовiрнiсть того, що вiдмовлять рiвно три елементи з п'яти. б) ![]() Ва- iмовiрнiсть того, що вiдмовлять не менш чотирьох елементiв з п'яти (тобто або чотири, або п'ять). в)
Ва- iмовiрнiсть того, що вiдмовлять не менш чотирьох елементiв з п'яти (тобто або чотири, або п'ять). в) ![]() Ва- iмовiрнiсть того, що вiдмовить хоча б один елемент (знайшли через iмовiрнiсть протилежноi подii - жоден елемент не вiдмовить).
Ва- iмовiрнiсть того, що вiдмовить хоча б один елемент (знайшли через iмовiрнiсть протилежноi подii - жоден елемент не вiдмовить).
№12. Скiльки варто зiграти партiй у шахи з iмовiрнiстю перемоги в однiй партii, рiвноi 1/3, щоб число перемог було дорiвнюi 5?
Рiшення: Число перемог k визначаiться з формули ![]() ВаТут p =1/3 (iмовiрнiсть перемоги), q = 2/3 (iмовiрнiсть програшу), n - невiдоме число партiй. Пiдставляючи даного значення, одержуiмо:
ВаТут p =1/3 (iмовiрнiсть перемоги), q = 2/3 (iмовiрнiсть програшу), n - невiдоме число партiй. Пiдставляючи даного значення, одержуiмо:
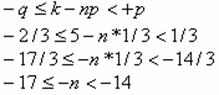
Одержуiмо, що n = 15, 16 або 17.
2. Локальна формула Муавра-Лапласа
Легко бачити, що користуватися формулою Бернуллi при бiльших значеннях n досить важко, тому що формула вимагаi виконання дiй над величезними числами. Природно, виникаi питання: чи не можна обчислити ймовiрнiсть, що цiкавить нас,, не прибiгаючи до формули Бернуллi.
В 1730 р. iнший метод рiшення при p=1/2 знайшов Муавр; в 1783 р. Лаплас узагальнив формулу Муавра для довiльного p, вiдмiнного вiд 0 i 1.
Ця формула застосовуiться при необмеженому зростаннi числа випробувань, коли ймовiрнiсть настання подii не занадто близька до нуля або одиницi. Тому теорему, про яку мова йде, називають теоремою Муавра-Лапласа.
Теорема Муавра-Лапласа. Якщо ймовiрнiсть p появи подii А в кожному випробуваннi постiйне й вiдмiнна вiд нуля й одиницi, то ймовiрнiсть ![]() Ватого, що подiя А з'явиться в n випробуваннях рiвно k раз, приблизно дорiвнюi(тим точнiше, чим бiльше n) значенню функцii
Ватого, що подiя А з'явиться в n випробуваннях рiвно k раз, приблизно дорiвнюi(тим точнiше, чим бiльше n) значенню функцii

При ![]() .
.
РД таблицi, у яких помiщенi значення функцii
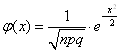 ,
,
вiдповiдним позитивним значенням аргументу x(див. додаток 1). Для негативних значень аргументу користуються тими ж таблицями, тому що функцiя ![]() Вапарна, тобто
Вапарна, тобто ![]() .
.
Отже, iмовiрнiсть того, що подiя A з'явиться в n незалежних випробуваннях рiвно k раз, приблизно дорiвнюi
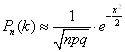 ,
,
де ![]() .
.
№13. Знайти ймовiрнiсть того, що подiя А наступить рiвно 80 разiв в 400 випробуваннях, якщо ймовiрнiсть появи цiii подii в кожному випробуваннi дорiвнюi 0,2.
Рiшення. За умовою n=400; k=80; p=0,2; q=0,8. Скористаiмося формулою Лапласа:
![]() .
.
Обчислимо обумовлене даними задачi значення x:
![]() .
.
По таблицi додатка 1 знаходимо ![]() .
.
Шукана ймовiрнiсть
![]() .
.
№14. РЖмовiрнiсть поразки мiшенi стрiльцем при одному пострiлi p=0,75.
Знайти ймовiрнiсть того, що при 10 пострiлах стрiлок уразить мiшень 8 разiв.
Рiшення. За умовою n=10; k=8; p=0,75; q=0,25.
Скористаiмося формулою Лапласа:
![]() .
.
Обчислимо обумовлене даними задачi значення x:
![]() .
.
По таблицi додатка 1 знаходимо
![]()
Шукана ймовiрнiсть
![]() .
.
№15. Знайти ймовiрнiсть того, що подiя А наступить рiвно 70 разiв в 243 випробуваннях, якщо ймовiрнiсть появи цiii подii в кожному випробуваннi дорiвнюi 0,25.
Рiшення. За умовою n=243; k=70; p=0,25; q=0,75. Скористаiмося формулою Лапласа:
![]() .
.
Знайдемо значення x:
![]() .
.
По таблицi додатка 1 знаходимо
![]() .
.
Шукана ймовiрнiсть
![]() .
.
№16. Знайти ймовiрнiсть того, що подiя А наступить 1400 разiв в 2400 випробуваннях, якщо ймовiрнiсть появи цiii подii в кожному випробуваннi дорiвнюi 0,6.
Рiшення. За умовою n=2400; k=1400; p=0,6; q=0,4. Як i в попередньому прикладi, скористаiмося формулою Лапласа:
![]()
Обчислимо x:
![]() .
.
По таблицi додатка 1 знаходимо
![]()
Шукана ймовiрнiсть
![]() .
.
3. Формула Пуассона
Ця формула застосовуiться при необмеженому зростаннi числа випробувань, коли ймовiрнiсть настання подii досить близька до 0 або 1.
![]() ,
,
![]() .
.
Доказ.
![]()
![]() .
.
![]() .
.
У такий спосiб одержали формулу:
![]() .
.
Приклади
№17. РЖмовiрнiсть виготовлення негiдноi деталi дорiвнюi 0,0002. Знайти ймовiрнiсть того, що серед 10000 деталей тiльки 2 деталi будуть негiдними.
Рiшення. n=10000; k=2; p=0,0002. ![]()
![]() .
.
№18. РЖмовiрнiсть виготовлення бракованоi деталi дорiвнюi 0,0004. Знайти ймовiрнiсть того, що серед 1000 деталей тiльки 5 деталi будуть бракованими.
Рiшення. n=1000; k=5; p=0,0004.
![]()
Шукана ймовiрнiсть
![]() .
.
№19. РЖмовiрнiсть виграшу лотереi дорiвнюi 0,0001. Знайти ймовiрнiсть того, що з 5000 спроб виграти вдасться 3 рази.
Рiшення. n=5000; k=3; p=0,0001.
![]()
Шукана ймовiрнiсть
![]() .
.
4. Теорема Бернуллi про частоту ймовiрностi
Теорема. РЖмовiрнiсть того, що в n незалежних випробуваннях, у кожному з яких iмовiрнiсть появи подii дорiвнюi p, абсолютна величина вiдхилення вiдносноi частоти появи подii вiд iмовiрностi появи подii не перевищить позитивного числа ![]() , приблизно дорiвнюi подвоiноi функцii Лапласа при
, приблизно дорiвнюi подвоiноi функцii Лапласа при ![]() :
:
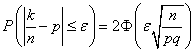 .
.
Доказ. Будемо вважати, що виробляiться n незалежних випробувань, у кожному з яких iмовiрнiсть появи подii А постiйна й дорiвнюi p. Поставимо перед собою задачу знайти ймовiрнiсть того, що вiдхилення вiдносноi частоти ![]() Вавiд постiйноi ймовiрностi p по абсолютнiй величинi не перевищуi заданого числа
Вавiд постiйноi ймовiрностi p по абсолютнiй величинi не перевищуi заданого числа ![]() . РЖнакше кажучи, знайдемо ймовiрнiсть здiйснення нерiвностi
. РЖнакше кажучи, знайдемо ймовiрнiсть здiйснення нерiвностi
![]() . (*)
. (*)
Замiнимо нерiвнiсть (*) йому рiвносильними:
![]() .
.
Множачи цi нерiвностi на позитивний множник ![]() , одержимо нерiвностi, рiвносильнi вихiдному:
, одержимо нерiвностi, рiвносильнi вихiдному:
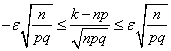 .
.
Тодi ймовiрнiсть знайдемо в такий спосiб:
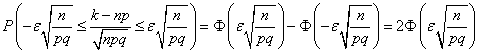 .
.
Значення функцii ![]() Ваперебуваi по таблицi(див. додаток 2).
Ваперебуваi по таблицi(див. додаток 2).
Приклади
№20. РЖмовiрнiсть того, що деталь не стандартна, p=0,1. Знайти ймовiрнiсть того, що серед випадково вiдiбраних 400 деталей вiдносна частота появи нестандартних деталей вiдхилиться вiд iмовiрностi p=0,1 по абсолютнiй величинi не бiльш, нiж на 0,03.
Рiшення. n=400; p=0,1; q=0,9; ![]() =0,03. Потрiбно знайти ймовiрнiсть
=0,03. Потрiбно знайти ймовiрнiсть![]() . Користуючись формулою
. Користуючись формулою
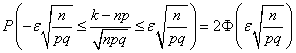 ,
,
маiмо
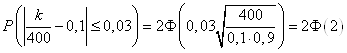 .
.
По таблицi додатка 2 знаходимо ![]() . Отже,
. Отже, ![]() . Отже, шукана ймовiрнiсть дорiвнюi 0,9544.
. Отже, шукана ймовiрнiсть дорiвнюi 0,9544.
№21. РЖмовiрнiсть того, що деталь не стандартна, p=0,1. Знайти, скiльки деталей треба вiдiбрати, щоб з iмовiрнiстю, рiвноi 0,9544, можна було затверджувати, що вiдносна частота появи нестандартних деталей(серед вiдiбраних) вiдхилиться вiд постiйноi ймовiрностi p по абсолютнiй величинi не бiльше нiж на 0,03.
Рiшення. За умовою, p=0,1; q=0,9; ![]() =0,03;
=0,03; ![]() . Потрiбно знайти n. Скористаiмося формулою
. Потрiбно знайти n. Скористаiмося формулою
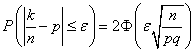 .
.
У силу умови

Отже,
![]()
По таблицi додатка 2 знаходимо ![]() . Для вiдшукання числа n одержуiмо рiвняння
. Для вiдшукання числа n одержуiмо рiвняння ![]() . Звiдси шукане число деталей n=400.
. Звiдси шукане число деталей n=400.
№22. РЖмовiрнiсть появи подii в кожному з незалежних випробувань дорiвнюi 0,2. Знайти, яке вiдхилення вiдносноi частоти появи подii вiд його ймовiрностi можна чекати з iмовiрнiстю 0,9128 при 5000 випробуваннях.
Рiшення. Скористаiмося тiiю же формулою, з якоi треба:
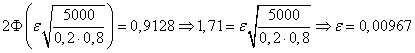 .
.
Лiтература
1. Гмурман Е.В. Теорiя ймовiрностей i математична статистика. тАУ К., 2003
2. Гмурман Е.В. Керiвництво до рiшення задач по теорii ймовiрностей i математичнiй статистицi. тАУ К., 2004.
3. Гнеденко Б.В. Курс теорii ймовiрностей. тАУ К., 2007.
4. Колемаiв В.А., Калiнiна В.Н., Соловйов В.И., Малихин В.РЖ., Курочкин О.П. Теорiя ймовiрностей у прикладах i задачах. тАУ К., 2004.
5. Вентцель Е.С. Теорiя ймовiрностей. тАУ К., 2004
Додатки
Додаток 1
Таблиця значень функцii ![]()

Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1.6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1.7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0648 | 0833 | 0818 | 0804 |
| 1.8 | 0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1.9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2.1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2.2 | 0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2.3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2.5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2.6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2.9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0043 |
| 3,0 | 0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 |