Поверхневi iнтеграли
ПОВЕРХНЕВРЖ РЖНТЕГРАЛИ
1. Поверхневi iнтеграли першого роду
Поверхневi iнтеграли першого роду i узагальненням подвiйних iнтегралiв.
Нехай у точках деякоi кусково-гладкоi поверхнi ![]() Вавизначена обмежена функцiя
Вавизначена обмежена функцiя ![]() . (Поверхня називаiться гладкою, якщо в кожнiй ii точцi iснуi дотична площина i при переходi вiд точки до точки положення цiii дотичноi площини змiнюiться неперервно. Поверхня, яка складаiться iз скiнченного числа неперервно зтАЩiднаних гладких поверхонь, називаiться кусково-гладкою.) Розiб'iмо поверхню
. (Поверхня називаiться гладкою, якщо в кожнiй ii точцi iснуi дотична площина i при переходi вiд точки до точки положення цiii дотичноi площини змiнюiться неперервно. Поверхня, яка складаiться iз скiнченного числа неперервно зтАЩiднаних гладких поверхонь, називаiться кусково-гладкою.) Розiб'iмо поверхню ![]() Вана
Вана ![]() Вадовiльних частин
Вадовiльних частин ![]() Вабез спiльних внутрiшнiх точок (рис. 1); нехай
Вабез спiльних внутрiшнiх точок (рис. 1); нехай ![]() ВатАУ площа, а
ВатАУ площа, а ![]() ВатАУ дiаметр частини поверхнi
ВатАУ дiаметр частини поверхнi ![]() . У кожнiй частинi
. У кожнiй частинi ![]() Вавиберемо довiльну точку
Вавиберемо довiльну точку ![]() Ваi складемо суму
Ваi складемо суму
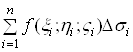 .(1)
.(1)
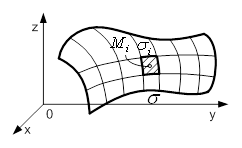
Рисунок 1 тАУ Поверхня ![]()
Цю суму називають iнтегральною сумою для функцii ![]() Вапо поверхнi
Вапо поверхнi ![]() .
.
Якщо при ![]() Ваiнтегральнi суми (1) мають скiнченну межу, яка не залежить нi вiд способу розбиття поверхнi
Ваiнтегральнi суми (1) мають скiнченну межу, яка не залежить нi вiд способу розбиття поверхнi ![]() , нi вiд вибору точок
, нi вiд вибору точок ![]() , цю границю називають поверхневим iнтегралом першого роду вiд функцii
, цю границю називають поверхневим iнтегралом першого роду вiд функцii ![]() Вапо поверхнi
Вапо поверхнi ![]() Ваi позначають
Ваi позначають ![]() .
.
Таким чином, за означенням
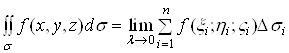 .(2)
.(2)
У цьому разi функцiя ![]() Ваназиваiться iнтегровною по поверхнi
Ваназиваiться iнтегровною по поверхнi ![]() , а поверхня
, а поверхня ![]() ВатАУ областю iнтегрування.
ВатАУ областю iнтегрування.
Якщо функцiя ![]() Ванеперервна на поверхнi
Ванеперервна на поверхнi ![]() , то вона iнтегровна по
, то вона iнтегровна по ![]() .
.
Обчислення поверхневого iнтеграла першого роду зводиться до обчислення подвiйного iнтеграла.
Нехай гладка поверхня ![]() , задана рiвнянням
, задана рiвнянням ![]() , проектуiться на площину
, проектуiться на площину ![]() Вав область
Вав область ![]() . Припустимо, що функцiя
. Припустимо, що функцiя ![]() Ванеперервна на поверхнi
Ванеперервна на поверхнi ![]() , а функцii
, а функцii ![]() Ванеперервнi в областi
Ванеперервнi в областi ![]() .
.
Внаслiдок розбиття поверхнi ![]() Вана частини
Вана частини ![]() Ваобласть
Ваобласть ![]() Варозiб'iться на частини
Варозiб'iться на частини ![]() , якi i вiдповiдними проекцiями частин
, якi i вiдповiдними проекцiями частин ![]() Вана площину
Вана площину ![]() Ва(рис. 2).
Ва(рис. 2).
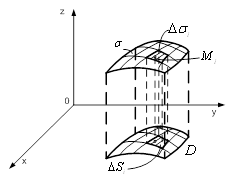
Рисунок 2 тАУ Розбиття поверхнi ![]() Вана частини
Вана частини ![]()
Якщо ![]() ВатАУ площа областi
ВатАУ площа областi ![]() ,
, ![]() ВатАУ площа поверхнi
ВатАУ площа поверхнi ![]() , то
, то
![]() ,
,
тому iнтегральну суму (1) можна записати у виглядi
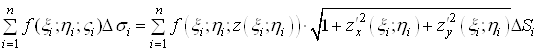 .(3)
.(3)
Права частина цiii рiвностi i iнтегральною сумою для функцii
![]() ,
,
тому з рiвностей (2) i (3) випливаi, що
![]() .(4)
.(4)
Формула (4) виражаi поверхневий iнтеграл першого роду через подвiйний iнтеграл по проекцii поверхнi ![]() Вана площину
Вана площину ![]() .
.
Аналогiчно можна отримати формули, що виражають iнтеграл по поверхнi ![]() Вачерез подвiйнi iнтеграли по ii проекцiях на площини
Вачерез подвiйнi iнтеграли по ii проекцiях на площини ![]() Вата
Вата ![]() . Якщо поверхня
. Якщо поверхня ![]() Вазадаiться рiвнянням
Вазадаiться рiвнянням ![]() Ваабо
Ваабо ![]() , то
, то
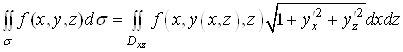
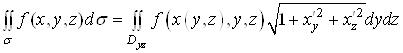 ,
,
де ![]() Вата
Вата ![]() ВатАУ проекцii поверхнi
ВатАУ проекцii поверхнi ![]() Вана координатнi площини
Вана координатнi площини ![]() Вата
Вата ![]() Вавiдповiдно.
Вавiдповiдно.
Якщо у формулi (2) покласти ![]() Вана поверхнi
Вана поверхнi ![]() , то отримаiмо
, то отримаiмо
![]() ,(5)
,(5)
де ![]() ВатАУ площа поверхнi
ВатАУ площа поверхнi ![]() , тобто за допомогою поверхневого iнтеграла першого роду можна обчислювати площi поверхонь.
, тобто за допомогою поверхневого iнтеграла першого роду можна обчислювати площi поверхонь.
Крiм того, поверхневi iнтеграли першого роду застосовують при обчисленнi маси, координат центра маси, моменту iнерцii матерiальноi поверхнi з вiдомою поверхневою густиною розподiлу маси. Виведення вiдповiдних формул по сутi не вiдрiзняiться вiд виводу аналогiчних формул для матерiальноi пластинки.
Якщо на кусково-гладкiй поверхнi ![]() Варозподiлено масу з поверхневою густиною
Варозподiлено масу з поверхневою густиною ![]() , то:
, то:
а) маса матерiальноi поверхнi
![]() ;
;
б) координати центра маси поверхнi:
![]() ,
,
де ![]() ВатАУ статичнi моменти поверхнi
ВатАУ статичнi моменти поверхнi ![]() Вавiдносно осей
Вавiдносно осей ![]() ;
;
в) моменти iнерцii поверхнi вiдносно осей координат i початку координат:
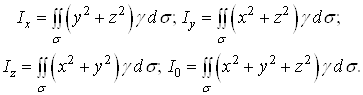
2. Поверхневi iнтеграли другого роду
Введемо поняття сторони поверхнi. Вiзьмемо на гладкiй поверхнi ![]() Вадовiльну точку
Вадовiльну точку ![]() , проведемо в нiй нормаль
, проведемо в нiй нормаль ![]() Вапевного напряму i розглянемо на поверхнi
Вапевного напряму i розглянемо на поверхнi ![]() Вадовiльний замкнений контур, який виходить з точки
Вадовiльний замкнений контур, який виходить з точки ![]() Ваi повертаiться в точку
Ваi повертаiться в точку ![]() , не перетинаючи при цьому межi поверхнi
, не перетинаючи при цьому межi поверхнi ![]() . Перемiщатимемо точку
. Перемiщатимемо точку ![]() Вапо замкненому контуру разом з вектором
Вапо замкненому контуру разом з вектором ![]() Ватак, щоб вектор
Ватак, щоб вектор ![]() Вавесь час залишався нормальним до
Вавесь час залишався нормальним до ![]() . При обходi заданого контуру ми можемо повернутися в точку
. При обходi заданого контуру ми можемо повернутися в точку ![]() Ваз тим самим або з протилежним напрямом нормалi.
Ваз тим самим або з протилежним напрямом нормалi.
Якщо у довiльну точку ![]() Ваповерхнi
Ваповерхнi ![]() Вапiсля обходу довiльного замкненого контуру, розмiщеного на поверхнi
Вапiсля обходу довiльного замкненого контуру, розмiщеного на поверхнi ![]() , який не перетинаi ii межу, ми повертаiмося з початковим напрямом нормалi
, який не перетинаi ii межу, ми повертаiмося з початковим напрямом нормалi ![]() , то поверхню називають двосторонньою.
, то поверхню називають двосторонньою.
Якщо при обходi деякого контуру напрям нормалi змiнюiться на протилежний, то поверхню називають односторонньою.
Прикладами двостороннiх поверхонь i площина, сфера, довiльна замкнена поверхня без самоперетинiв, довiльна поверхня, задана рiвнянням ![]() , де
, де ![]() ВатАУ функцii, неперервнi в деякiй областi
ВатАУ функцii, неперервнi в деякiй областi ![]() Ваплощини
Ваплощини ![]() .
.
Прикладом односторонньоi поверхнi i так званий лист Мебiуса (рис. 3).

Рисунок 3 тАУ Лист Мебiуса
Модель цiii поверхнi можна отримати, якщо прямокутну полоску паперу![]() , перекрутивши один раз, склеiти так, щоб точка
, перекрутивши один раз, склеiти так, щоб точка ![]() Вазбiгалася з
Вазбiгалася з ![]() , а точка
, а точка ![]() ВатАУ з
ВатАУ з ![]() .
.
Двосторонню поверхню називають орiiнтовною, а вибiр певноi ii сторони орiiнтацiiю поверхнi. Направивши в кожнiй точцi замкненоi поверхнi нормаль всередину об'iму, обмеженого поверхнею, отримаiмо внутрiшню сторону поверхнi, а направивши нормаль зовнi поверхнi-зовнiшню ii сторону. Надалi розглядатимемо двостороннi поверхнi. Одностороннi поверхнi неорiiнтовнi.
Нехай ![]() ВатАУ орiiнтовна (сторона уже обрана) поверхня, обмежена контуром
ВатАУ орiiнтовна (сторона уже обрана) поверхня, обмежена контуром ![]() , який не маi точок самоперетину. Вважатимемо за додатний той напрям обходу контуру
, який не маi точок самоперетину. Вважатимемо за додатний той напрям обходу контуру ![]() , при якому спостерiгач, розмiщений так, що напрям нормалi збiгаiться з напрямом вiд нiг до голови при русi, залишаi поверхню злiва вiд себе (рис. 4).
, при якому спостерiгач, розмiщений так, що напрям нормалi збiгаiться з напрямом вiд нiг до голови при русi, залишаi поверхню злiва вiд себе (рис. 4).
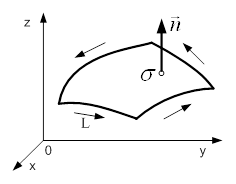
Рисунок 4 тАУ Орiiнтовна поверхня ![]()
Протилежний напрям обходу називаiться вiд'iмним. Якщо змiнити орiiнтацiю поверхнi на протилежну, то додатний i вiд'iмний напрями обходу контуру ![]() Вапомiняються мiсцями.
Вапомiняються мiсцями.
З'ясуiмо тепер поняття поверхневого iнтеграла другого роду.
Нехай ![]() ВатАУ гладка поверхня, задана рiвнянням
ВатАУ гладка поверхня, задана рiвнянням ![]() Ваi
Ваi ![]() ВатАУ обмежена функцiя, визначена в точках поверхнi
ВатАУ обмежена функцiя, визначена в точках поверхнi ![]() . Зорiiнтуiмо поверхню
. Зорiiнтуiмо поверхню ![]() . Розiб'iмо ii довiльно на
. Розiб'iмо ii довiльно на ![]() Вачастин. Позначимо через
Вачастин. Позначимо через ![]() Вапроекцiю
Вапроекцiю ![]() -i частини поверхнi
-i частини поверхнi ![]() Вана площину
Вана площину ![]() , а через
, а через ![]() ВатАУ площу
ВатАУ площу ![]() , взяту iз знаком плюс, якщо обрана зовнiшня сторона поверхнi
, взяту iз знаком плюс, якщо обрана зовнiшня сторона поверхнi ![]() , та iз знаком мiнус, якщо обрана внутрiшня сторона поверхнi
, та iз знаком мiнус, якщо обрана внутрiшня сторона поверхнi ![]() . Виберемо в кожнiй частинi
. Виберемо в кожнiй частинi ![]() Вадовiльну точку
Вадовiльну точку ![]() Ваi складемо суму
Ваi складемо суму
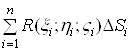 .(6)
.(6)
Вираз (6) називаiться iнтегральною сумою. Нехай ![]() ВатАУ максимальний дiаметр поверхонь
ВатАУ максимальний дiаметр поверхонь ![]() .
.
Якщо при ![]() Ваiнтегральнi суми (6) мають скiнченну границю, яка не залежить нi вiд способу розбиття поверхнi
Ваiнтегральнi суми (6) мають скiнченну границю, яка не залежить нi вiд способу розбиття поверхнi ![]() , нi вiд вибору точок
, нi вiд вибору точок ![]() , то цю границю називають поверхневим iнтегралом другого роду i позначають так:
, то цю границю називають поверхневим iнтегралом другого роду i позначають так: ![]() . Отже, за означенням
. Отже, за означенням
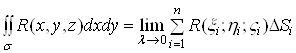 .(7)
.(7)
З означення поверхневого iнтеграла другого роду випливаi, що при змiнi сторони поверхнi на протилежну iнтеграл змiнюi знак, бо змiнюi знак ![]() .
.
Поверхню ![]() Ваможна також проектувати на координатнi площини
Ваможна також проектувати на координатнi площини ![]() Вата
Вата ![]() . Тодi матимемо ще два поверхневi iнтеграли
. Тодi матимемо ще два поверхневi iнтеграли ![]() , де
, де ![]() ВатАУ функцii, визначенi в точках поверхнi
ВатАУ функцii, визначенi в точках поверхнi ![]() .
.
Оскiльки ![]() Ва(рис. 5),
Ва(рис. 5),
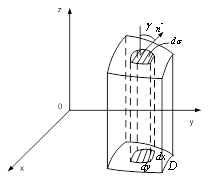
Рисунок 5 тАУ Проекцiя поверхнi ![]() Вана координатну площину
Вана координатну площину ![]()
де ![]() ВатАУ елемент площi поверхнi
ВатАУ елемент площi поверхнi ![]() ВатАУ кути мiж нормаллю до поверхнi
ВатАУ кути мiж нормаллю до поверхнi ![]() Вата осями
Вата осями ![]() Вавiдповiдно, то справедливi такi формули:
Вавiдповiдно, то справедливi такi формули:
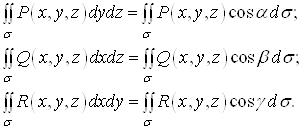
На практицi найпоширенiшими i поверхневi iнтеграли, якi об'iднують усi названi, тобто
![]() .(8)
.(8)
Якщо, наприклад, вектор ![]() Ваi швидкiстю рiдини, то кiлькiсть
Ваi швидкiстю рiдини, то кiлькiсть ![]() Варiдини, яка протiкаi через поверхню
Варiдини, яка протiкаi через поверхню ![]() Ваза одиницю часу, називаiться потоком вектора
Ваза одиницю часу, називаiться потоком вектора ![]() Вачерез поверхню
Вачерез поверхню ![]() Ваi знаходиться за формулою:
Ваi знаходиться за формулою:
![]() .
.
У цьому полягаi фiзичний змiст поверхневого iнтеграла другого роду. Зрозумiло, коли вектор ![]() Вамаi iншу природу, поверхневий iнтеграл маi iнший фiзичний змiст.
Вамаi iншу природу, поверхневий iнтеграл маi iнший фiзичний змiст.
Формула (8) виражаi загальний поверхневий iнтеграл другого роду через поверхневий iнтеграл першого роду.
Поверхневi iнтеграли другого роду обчислюються за допомогою подвiйних iнтегралiв.
Нехай функцiя ![]() Ванеперервна в усiх точках гладкоi поверхнi
Ванеперервна в усiх точках гладкоi поверхнi ![]() , яка задана рiвнянням
, яка задана рiвнянням ![]() , де область
, де область ![]() ВатАУ проекцiя поверхнi
ВатАУ проекцiя поверхнi ![]() Вана площину
Вана площину ![]() . Виберемо верхню сторону поверхнi
. Виберемо верхню сторону поверхнi ![]() , де нормаль до поверхнi утворюi з вiссю
, де нормаль до поверхнi утворюi з вiссю ![]() Вагострий кут, тодi
Вагострий кут, тодi ![]() . Оскiльки
. Оскiльки ![]() , то суму (6) можна записати у виглядi
, то суму (6) можна записати у виглядi
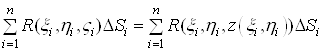 . (9)
. (9)
У правiй частинi рiвностi (9) мiститься iнтегральна сума для функцii ![]() . Ця функцiя неперервна в областi
. Ця функцiя неперервна в областi ![]() , тому iнтегрована в нiй.
, тому iнтегрована в нiй.
Перейшовши в рiвностi (9) до границi при ![]() , отримаiмо формулу
, отримаiмо формулу
![]() ,
,
яка виражаi поверхневий iнтеграл другого роду по змiнних ![]() Ваi
Ваi ![]() Вачерез подвiйний. Якщо вибрати нижню сторону поверхнi (нормаль до поверхнi утворюi з вiссю
Вачерез подвiйний. Якщо вибрати нижню сторону поверхнi (нормаль до поверхнi утворюi з вiссю ![]() Ватупий кут), то одержаний подвiйний iнтеграл беруть iз знаком ВлмiнусВ», тому
Ватупий кут), то одержаний подвiйний iнтеграл беруть iз знаком ВлмiнусВ», тому
![]() .(10)
.(10)
Аналогiчно
![]() ;(11)
;(11)
![]() .(12)
.(12)
У формулi (11) гладку поверхню ![]() Вазадано рiвнянням
Вазадано рiвнянням ![]() , а у формулi (12) тАУ рiвнянням
, а у формулi (12) тАУ рiвнянням ![]() . Знак ВлплюсВ» беремо у цих формулах тодi, коли нормаль до поверхнi утворюi вiдповiдно з вiссю
. Знак ВлплюсВ» беремо у цих формулах тодi, коли нормаль до поверхнi утворюi вiдповiдно з вiссю ![]() , з вiссю
, з вiссю ![]() Вагострий кут, а знак ВлмiнусВ» тАУ коли тупий кут;
Вагострий кут, а знак ВлмiнусВ» тАУ коли тупий кут; ![]() ,
, ![]() ВатАУ проекцii поверхнi
ВатАУ проекцii поверхнi ![]() Вана площини
Вана площини ![]() Вата
Вата ![]() Вавiдповiдно.
Вавiдповiдно.
Для обчислення загального iнтеграла (8) використовують формули (10) тАУ (12), проектуючи поверхню ![]() Вана всi три координатнi площини. Таким чином,
Вана всi три координатнi площини. Таким чином,
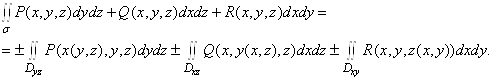
Правильнiсть вибору знакiв перед подвiйними iнтегралами можна перевiрити за допомогою формули
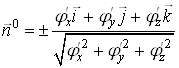 ,
,
яка визначаi одиничний нормальний вектор до поверхнi ![]() . Подвiйний знак у цiй формулi вiдповiдаi двом сторонам поверхнi
. Подвiйний знак у цiй формулi вiдповiдаi двом сторонам поверхнi ![]() . З формули (8) випливаi, що знак перед подвiйним iнтегралом збiгаiться iз знаком вiдповiдного напрямного косинуса нормалi
. З формули (8) випливаi, що знак перед подвiйним iнтегралом збiгаiться iз знаком вiдповiдного напрямного косинуса нормалi ![]() :
:
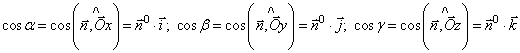 .
.
Якщо поверхня ![]() Ванеоднозначно проектуiться на будь-яку координатну площину, то цю поверхню розбивають на частини, а iнтеграл (8) тАУ на суму iнтегралiв по одержаних частинах поверхнi
Ванеоднозначно проектуiться на будь-яку координатну площину, то цю поверхню розбивають на частини, а iнтеграл (8) тАУ на суму iнтегралiв по одержаних частинах поверхнi ![]() .
.
3. Формула Остроградського-Гаусса
Формула Остроградського-Гаусса встановлюi зв'язок мiж поверхневим iнтегралом по замкненiй поверхнi i потрiйним iнтегралом по просторовiй областi, обмеженiй цiiю поверхнею. Ця формула i аналогом формули Грiна, яка, як вiдомо, встановлюi зв'язок криволiнiйного iнтеграла по замкненому контуру з подвiйним iнтегралом по плоскiй областi, обмеженiй цим контуром.
Нехай замкнена область ![]() Ваобмежена замкненою поверхнею
Ваобмежена замкненою поверхнею ![]() , причому знизу та зверху обмежена гладкими поверхнями
, причому знизу та зверху обмежена гладкими поверхнями ![]() Вата
Вата ![]() , рiвняння яких
, рiвняння яких ![]() Вата
Вата ![]() Ва(рис. 7).
Ва(рис. 7).
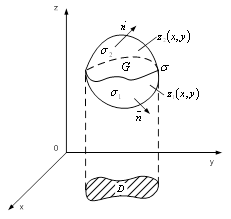
Рисунок 7 тАУ Замкнена область ![]()
Припустимо, що проекцiiю областi ![]() Вана площину
Вана площину ![]() Ваi область
Ваi область ![]() . Нехай в областi
. Нехай в областi ![]() Вавизначено неперервну функцiю
Вавизначено неперервну функцiю ![]() , яка в цiй областi маi неперервну похiдну
, яка в цiй областi маi неперервну похiдну ![]() .
.
Розглянемо потрiйний iнтеграл
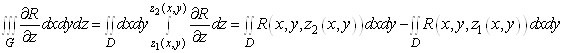 .
.
У правiй частинi цiii рiвностi перший подвiйний iнтеграл запишемо за допомогою поверхневого iнтеграла по зовнiшнiй сторонi поверхнi ![]() , а другий подвiйний iнтеграл тАУ по зовнiшнiй сторонi поверхнi
, а другий подвiйний iнтеграл тАУ по зовнiшнiй сторонi поверхнi ![]() . Враховуючи кути мiж нормаллю
. Враховуючи кути мiж нормаллю ![]() Вата вiссю
Вата вiссю ![]() , отримуiмо
, отримуiмо
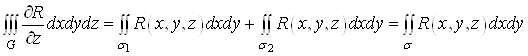 .(13)
.(13)
Аналогiчно, припустивши, що функцii ![]() ,
, 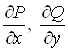 Ванеперервнi в областi
Ванеперервнi в областi ![]() , можна отримати формули
, можна отримати формули
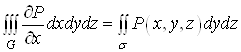 ,(14)
,(14)
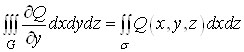 .(15)
.(15)
Додавши почленно рiвностi (13), (14) i (15), отримаiмо формулу
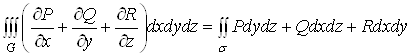 ,(16)
,(16)
яку називають формулою Остроградського-Гаусса. Ця формула справедлива i для довiльноi областi ![]() , яку можна розбити на скiнченне число областей, для яких виконуються рiвностi (13) тАУ (15).
, яку можна розбити на скiнченне число областей, для яких виконуються рiвностi (13) тАУ (15).
За допомогою формули Остроградського-Гаусса зручно обчислювати поверхневi iнтеграли по замкнених поверхнях.
4. Формула Стокса
Формула Стокса встановлюi зв'язок мiж поверхневим i криволiнiйним iнтегралами. Нехай ![]() ВатАУ поверхня, задана рiвнянням
ВатАУ поверхня, задана рiвнянням ![]() , причому функцii
, причому функцii ![]() ВатАУ неперервнi в областi
ВатАУ неперервнi в областi ![]() ВатАУ проекцii поверхнi
ВатАУ проекцii поверхнi ![]() Вана площину
Вана площину ![]() ;
; ![]() ВатАУ контур, який обмежуi
ВатАУ контур, який обмежуi ![]() , а
, а ![]() ВатАУ проекцiя контуру
ВатАУ проекцiя контуру ![]() Вана площину
Вана площину ![]() , тобто
, тобто ![]() ВатАУ межа областi
ВатАУ межа областi ![]() .
.
Виберемо верхню сторону поверхнi ![]() Ва(рис. 8).
Ва(рис. 8).
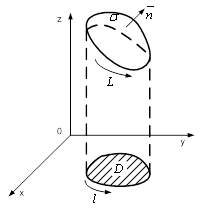
Рисунок 8 тАУ Поверхня ![]()
Якщо функцiя ![]() Ванеперервна разом iз своiми частинними похiдними першого порядку на поверхнi
Ванеперервна разом iз своiми частинними похiдними першого порядку на поверхнi ![]() , то справедлива формула
, то справедлива формула
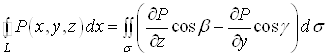 .(17)
.(17)
поверхневий iнтеграл формула стокс
Доведення
Перетворимо криволiнiйний iнтеграл, який мiститься у лiвiй частинi рiвностi (17). Оскiльки контур ![]() Валежить на поверхнi
Валежить на поверхнi ![]() , то координати його точок задовольняють рiвняння
, то координати його точок задовольняють рiвняння ![]() , i тому значення функцii
, i тому значення функцii ![]() Вау точках контуру
Вау точках контуру ![]() Вадорiвнюють значенням функцii
Вадорiвнюють значенням функцii ![]() Вау вiдповiдних точках контуру
Вау вiдповiдних точках контуру ![]() . Звiдси випливаi, що
. Звiдси випливаi, що
![]() .
.
Застосовуючи до знайденого iнтеграла формулу Грiна, отримаiмо
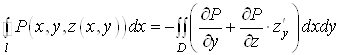 .
.
Тут пiдiнтегральна функцiя дорiвнюi частиннiй похiднiй по ![]() Вавiд складеноi функцii
Вавiд складеноi функцii ![]() .
.
Оскiльки ![]() ВатАУ верхня сторона поверхнi, тобто
ВатАУ верхня сторона поверхнi, тобто ![]() Ва(
Ва(![]() ВатАУ гострий кут мiж нормаллю
ВатАУ гострий кут мiж нормаллю ![]() Вадо поверхнi
Вадо поверхнi ![]() Ваi вiссю
Ваi вiссю ![]() ), то нормаль маi проекцii
), то нормаль маi проекцii ![]() . Але напрямнi косинуси нормалi пропорцiйнi вiдповiдним проекцiям, тому
. Але напрямнi косинуси нормалi пропорцiйнi вiдповiдним проекцiям, тому
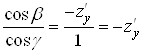 ,
,
Тодi
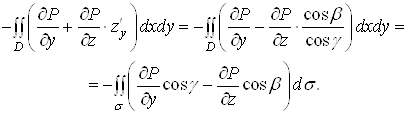
Отже,
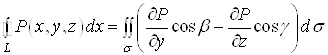 .
.
Аналогiчно можна довести, що при вiдповiдних умовах справедливi формули:
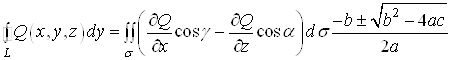 ;(18)
;(18)
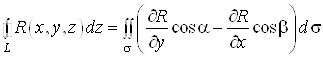 .(19)
.(19)
Додаючи почленно рiвностi (17), (18) i (19), отримуiмо формулу
![]() ,
,
яка називаiться формулою Стокса. За допомогою формули (8), яка пов'язуi поверхневi iнтеграли першого та другого роду, цю формулу можна записати так:
![]() (20)
(20)
Формула Стокса даi змогу обчислювати криволiнiйнi iнтеграли по замкнутих контурах за допомогою поверхневих iнтегралiв.
З формули Стокса випливаi, що коли виконуються рiвностi
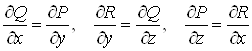 ,(21)
,(21)
то криволiнiйний iнтеграл по довiльному просторовому замкненому контуру ![]() Вадорiвнюi нулю:
Вадорiвнюi нулю:
![]() .(22)
.(22)
А це означаi, що в даному випадку криволiнiйний iнтеграл не залежить вiд форми контура iнтегрування.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики