Представлення i перетворення фiгур

ПРЕДСТАВЛЕННЯ РЖ ПЕРЕТВОРЕННЯ ТОЧОК

Представлення точок здiйснюiться наступним чином:

На площинi

У просторi

Перетворення точок.

Розглянемо результати матричного множення , що визначаi точку Р, i матрицi перетворення 2х2 загального виду:

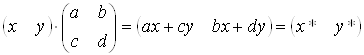(3.1)

Дослiдимо декiлька часткових випадкiв.

1) а=d=1 i c==0. Змiн не вiдбуваiться

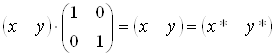.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (3.2)

2) d=1, =c=0. Змiна масштабу по осi x

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.3)

3) =c=0. Змiна масштабу по осях x i y

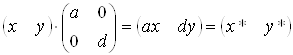.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (3.4)

4) =c=0, d=1, a=-1. Вiдображення координат вiдносно осi y

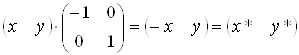.ВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (3.5)

5) =c=0, a=d<0. Вiдображення вiдносно початку координат

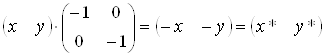.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.6)

6) а=d=1,c=0. Зсув

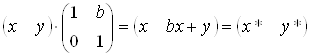.ВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.7)

Для початку координат маiмо iнварiантно

.

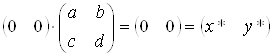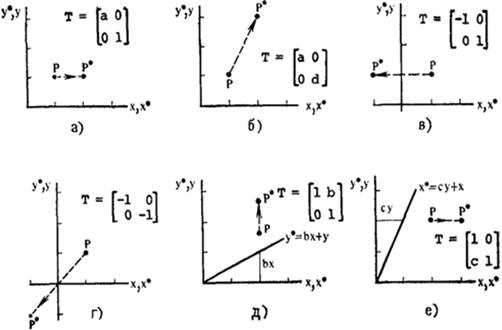
Рис.3.1. Перетворення точок.

ПЕРЕТВОРЕННЯ ПРЯМИХ ЛРЖНРЖЙ

Пряма задана 2 векторами.

Вектори положення точок А i В рiвнi Ваi .

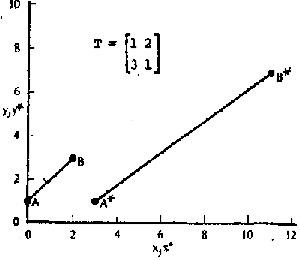
Рис.3.2. Перетворення прямих лiнiй.

Матриця перетворення

.

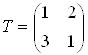Одержимо:

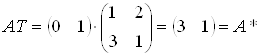,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.8)

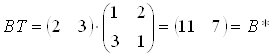.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.9)

Альтернативне представлення лiнii AB

.

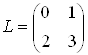Пiсля цього множення матрицi L на Т дасть

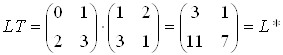.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.10)

Операцiя зсуву збiльшила довжину лiнii i змiнила ii положення.

ОБЕРТАННЯ

Розглянемо плоский трикутник ABC.

Здiйснимо поворот на 90В° проти годинниковоi стрiлки.

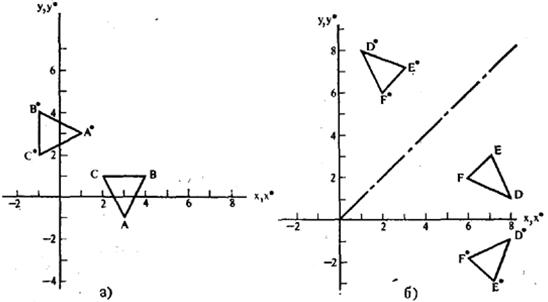
Рис.3.3. Обертання i вiдображення.

Одержимо

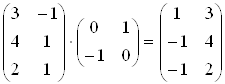.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.11)

В результатi отримаiмо трикутник A*B*C*. Поворот на 180В° задаiться матрицею

,

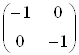поворот на 270В° навколо початку координат - за допомогою матрицi:

.

ВРЖДОБРАЖЕННЯ

Вiдображення визначаiться поворотом на 180В° навколо осi, що лежить у площинi ху.

1) Обертання навколо прямоi y=x задаiться матрицею:

.

Новi вирази визначаються спiввiдношенням:

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.12)

2) Обертання навколо осi y=0 задаiться матрицею:

.

Новi вершини визначаються спiввiдношенням:

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.13)

ЗМРЖНА МАСШТАБУ

Змiна масштабу визначаiться значенням 2-х елементiв головноi дiагоналi матрицi.

Якщо використовуiмо матрицю Вамаiмо збiльшення в 2 рази.

Якщо значення елементiв не рiвнi, то маi мiсце спотворення.

Трикутник ABC перетворений за допомогою матрицi . Трикутник DEF перетворений за допомогою матрицi 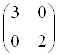. Маiмо спотворення.

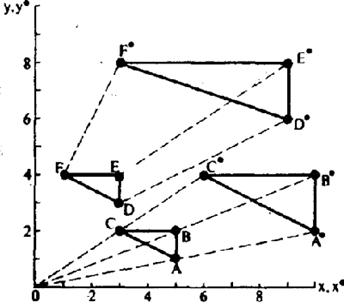
Рис.3.4. Рiвномiрна i нерiвномiрна змiна масштабiв.

ДВОВИМРЖРНИЙ ЗСУВ РЖ ОДНОРРЖДНРЖ КООРДИНАТИ

Введемо третiй компонент у вектори точок Ваi -Ваi .

Матриця перетворення матиме вигляд:

перетворення фiгура площина точка

.

Таким чином,

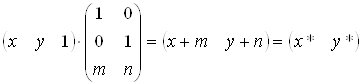.ВаВаВаВаВаВаВаВаВаВа (3.14)

Константи m, викликають зсув x* i y* вiдносно x i y.

Матриця 3х2 не квадратна - вона не маi оберненоi матрицi.

Доповнимо матрицю перетворення до квадратноi

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.15)

Третiй компонент не змiнюiться.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики