Напрямки теорii ймовiрностей та математичнi дii над ними
Контрольна робота з теми:
Напрямки теорii ймовiрностей та математичнi дii над ними
1. Основнi напрямки теорii ймовiрностей. Безпосереднiй пiдрахунок ймовiрностей
Подiiю (або випадковою подiiю) називаiться будь-який факт, що внаслiдок експерименту може вiдбутися або не вiдбутися.
Ймовiрнiстю подii називаiться чисельна мiра ступеня об'iктивноi можливостi цiii подii. Ймовiрнiсть подii А позначаiться 
.
Достовiрною i подiя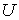 
, яка внаслiдок експерименту неодмiнно повинна вiдбутися:
.
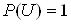Неможливою i подiя, яка внаслiдок експерименту не може вiдбутися:
.
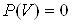Ймовiрнiсть будь-якоi подii знаходиться мiж нулем та одиницею:
.
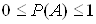Декiлька подiй утворюють повну групу, якщо внаслiдок експерименту неодмiнно повинна вiдбутися хоча б одна з них, тобто поява хоча б однiii з подiй повноi групи i достовiрна подiя.
Декiлька подiй в даному експериментi називаються несумiсними, якщо поява однiii з них виключаi появу iншоi в одному i тому ж випробуваннi.
Декiлька подiй i рiвноймовiрними, якщо немаi пiдстав вважати яку-небудь з них бiльш можливою, нiж будь-яку iншу.
Кожний з можливих результатiв випробування i елементарним наслiдком. Вони утворюють повну групу, несумiснi та рiвноймовiрнi.
Елементарнi наслiдки i такими, що сприяють подii, якщо поява цих виходiв спричиняi появу подii.
Вiдповiдно до класичного визначення, ймовiрнiсть подii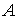 
Ваобчислюiться за формулою:
,
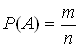де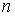 
ВатАУ загальне число елементарних наслiдкiв, 
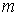ВатАУ число наслiдкiв, що сприяють подii .
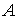При безпосередньому пiдрахунку ймовiрностей використовують основнi формули та правила комбiнаторики.
Перестановками i комбiнацii, що складаються з однакових елементiв i вiдрiзняються лише порядком розташування цих елементiв. Число всiх перестановок дорiвнюi :
.
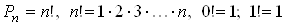Розмiщеннями i упорядкованi комбiнацii, що складаються з m рiзних елементiв даноi - елементноi множини. Число розмiщень дорiвнюi:
.
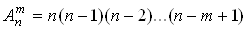Сполученнями i неупорядкованi комбiнацii, що складаються з m рiзних елементiв даноi - елементноi множини. Число сполучень дорiвнюi:
ймовiрнiсть теорiя теорема байiс
.
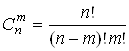Правило суми. Якщо деякий об'iкт А можна вибрати з сукупностi об'iктiв m способами, а iнший об'iкт В може бути вибраний способами, то вибрати або А, або В можна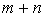 
Васпособами.
Правило множення. Якщо об'iкт А можна вибрати з сукупностi об'iктiв m способами, i пiсля кожного такого вибору об'iкт В можна вибрати способами, то пара об'iктiв А i В може бути вибрана 
Васпособами.
Приклад 1.
Кидають одночасно двi гральнi костi. Знайти ймовiрностi таких подiй:
1) А тАУ сума очок, що випали, дорiвнюi 8;
2) В тАУ добуток очок, що випали, дорiвнюi 8;
3) С тАУ сума очок, що випали, дорiвнюi 8, а добуток тАУ 15.
Розв'язок.
1) А тАУсума очок, що випали, дорiвнюi 8.
Загальне число можливих елементарних наслiдкiв експерименту дорiвнюi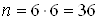 
, оскiльки кожна кiстка даi 6 наслiдкiв, а кожний з наслiдкiв кидання "першоi" костi може поiднуватися з кожним з наслiдкiв кидання "другоi" (правило множення). Наслiдки, що сприяють нашiй подii (сума очок дорiвнюi 8), i такi: (2;6), (3;5), (4;4), (5;3), (6;2), тобто 
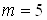. Шукана ймовiрнiсть дорiвнюi вiдношенню числа наслiдкiв, що сприяють подii, до числа всiх можливих елементарних наслiдкiв: 
.
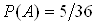2) В тАУ добуток очок, що випали, дорiвнюi 8.
Загальне число можливих елементарних наслiдкiв експерименту залишилося незмiнним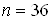 
, а число наслiдкiв, що сприяють подii В, дорiвнюi: 
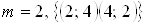. Тодi 
.
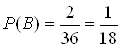3) С тАУ сума очок, що випали, дорiвнюi 8, добуток тАУ 15.
Загальне число можливих елементарних наслiдкiв експерименту залишилося 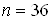. Сприяють шуканiй подii тiльки тi наслiдки, для яких виконуються двi умови: сума очок, що випали, дорiвнюi 8, а добуток тАУ 15: 
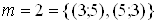. Тодi 
.
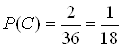Приклад 2.
У ящику 100 деталей, з них 10 бракованих. Навмання витягнули 4 деталi. Знайти ймовiрнiсть того, що серед витягнутих деталей рiвно 3 стандартнi.
РозвтАЩязок.
Подiя А тАУ серед витягнутих деталей рiвно 3 стандартнi.
Загальне число можливих наслiдкiв випробування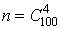 
Вадорiвнюi числу способiв, якими можна витягнути 4 деталi зi 100. Пiдрахуiмо число наслiдкiв, що сприяють нашiй подii. Три стандартнi деталi з 90 можна витягнути 
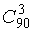Васпособами, а одна бракована деталь, що залишилася, може бути витягнута з 10 бракованих деталей 
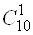Васпособами. Отже, число наслiдкiв, що сприяють нашiй подii, дорiвнюi:
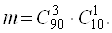Тодi шукана ймовiрнiсть дорiвнюi вiдношенню числа наслiдкiв, що сприяють подii, до числа всiх елементарних наслiдкiв:
.
Приклад 3.
На десяти картках написанi цифри: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Три з них виймаються навмання i викладаються на стiл у порядку появи. Знайти ймовiрнiсть того, що:
1) в порядку появи цифр вийде число 245;
2) з отриманих цифр можна скласти число 245.
РозвтАЩязок.
1) А тАУ в порядку появи цифр вийде число 245.
Число всiх елементарних наслiдкiв експерименту тАУ це число можливих розмiщень з 10 елементiв по три (отриманi комбiнацii елементiв можуть вiдрiзнятися одна вiд одноi або самими елементами, або iх порядком):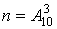 
.
З загального числа наслiдкiв експерименту тiльки один i для нашоi подii таким, що сприяi, тобто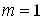 
. Шукана ймовiрнiсть:
.
2) В тАУ з отриманих цифр можна скласти число 245.
На вiдмiну вiд попередньоi задачi число можливих наслiдкiв експерименту обчислимо як число можливих сполучень з 10 по 3, оскiльки порядок появи елементiв не вiдiграi ролi, тобто елементи можна помiняти мiсцями. Шукана ймовiрнiсть:
Приклад
З п'яти букв розрiзноi азбуки складене слово "КНИГА". Дитина, що не вмii читати, розсипала цi букви i потiм склала в довiльному порядку. Знайти ймовiрнiсть того, що у неi знову вийшло слово "КНИГА".
РозвтАЩязок.
Подiя А тАУ вийшло слово "КНИГА".
Дитина може зiбрати в довiльному порядку тi п'ять букв, якi складають слово "КНИГА". Отриманi буквосполучення вiдрiзняються одне вiд iншого не самими елементами, а тiльки iх порядком, тому число всiх наслiдкiв експерименту обчислимо як число перестановок з п'яти елементiв: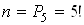 
З усiх можливих наслiдкiв експерименту тiльки один сприяi появi шуканоi подii А. Ймовiрнiсть дорiвнюi:
.
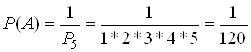Приклад 5.
Те ж завдання, але якщо було складене слово "РАКЕТА".
РозвтАЩязок.
В тАУ складене слово "РАКЕТА".
Загальне число наслiдкiв експерименту обчислимо як число перестановок з 6 (в заданому словi 6 букв) елементiв, тобто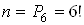 
ВаЗ усiх можливих наслiдкiв експерименту два сприяють появi знову слова РАКЕТА, оскiльки в цьому словi двi однаковi букви А i через змiну iх мiсць слово не змiниться. 
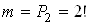ВаШукана ймовiрнiсть:
.
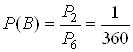2 .Теореми додавання та множення ймовiрностей
Сумою двох подiй А i В i подiя С, що вiдбуваiться у випадку появи хоча б однiii з подiй А або В.
Сумою декiлькох подiй i подiя, що вiдбуваiться у випадку появи хоча б однiii з цих подiй.
Добутком двох подiй А i В i подiя, що вiдбуваiться у разi спiльноi появи подii А та подii В.
Добутком декiлькох подiй i подiя, що вiдбуваiться у разi спiльноi появи усiх цих подiй.
Теорема. Ймовiрнiсть появи суми двох несумiсних подiй дорiвнюi сумi появ ймовiрностей цих подiй
.
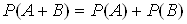Наслiдок. Ймовiрнiсть появи суми декiлькох попарно несумiсних подiй дорiвнюi сумi ймовiрностей цих подiй
.
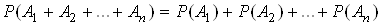Теорема. Сума ймовiрностей подiй,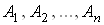 
, що створюють повну групу, дорiвнюi одиницi
.
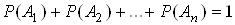Подiя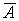 
Ваi протилежною до подii А, якщо вона полягаi в тому, що подiя А не вiдбулася.
Теорема. Сума ймовiрностей протилежних подiй дорiвнюi одиницi:
.
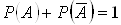Прийнятi такi позначення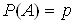 
, 
.
Теорема. Ймовiрнiсть спiльноi появи двох подiй дорiвнюi добутку ймовiрностi однiii з них на умовну ймовiрнiсть iншоi, обчислену в припущеннi, що перша подiя вже вiдбулася:
,
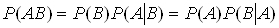де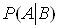 
ВатАУ умовна ймовiрнiсть подii А за умови, що подiя В вiдбулася, 
ВатАУ умовна ймовiрнiсть подii В за умови, що подiя А вiдбулася.
Наслiдок. Ймовiрнiсть спiльноi появи декiлькох подiй дорiвнюi добутку ймовiрностi однiii з них на умовнi ймовiрностi всiх iнших, причому ймовiрнiсть кожноi подальшоi подii обчислюються в припущеннi, що всi попереднi подii вже вiдбулися:
.
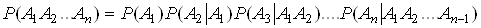Подiя В i незалежною вiд подii А, якщо поява подii А не змiнюi ймовiрностi появи подii В, тобто якщо умовна ймовiрнiсть подii В дорiвнюi ii безумовнiй iмовiрностi.
Теорема. Ймовiрнiсть спiльноi появи двох незалежних подiй дорiвнюi добутку ймовiрностей цих подiй:
.
Наслiдок. Ймовiрнiсть спiльноi появи декiлькох подiй, незалежних в сукупностi, дорiвнюi добутку ймовiрностей цих подiй:
.
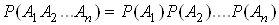Теорема. Ймовiрнiсть появи хоча б однiii з подiй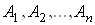 
, незалежних в сукупностi, дорiвнюi рiзницi мiж одиницею i добутком ймовiрностей протилежних подiй 
:
.
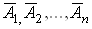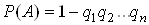Окремий випадок. Якщо подii 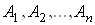Вамають однакову ймовiрнiсть, яка дорiвнюi р, то ймовiрнiсть появи хоча б однiii з цих подiй дорiвнюi:
.
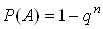Теорема. Ймовiрнiсть появи хоча б однiii з двох сумiсних подiй дорiвнюi сумi ймовiрностей цих подiй без iмовiрностi iх спiльноi появи:
.
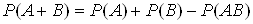Приклад 1.
Ймовiрнiсть влучення у цiль при одному пострiлi з першоi гармати дорiвнюi 0,7, другоi тАУ 0,8. Знайти ймовiрнiсть влучення у цiль при одному залпi з обох гармат.
РозвтАЩязок.
Визначимо подii: А тАУ перша гармата влучила при одному пострiлi, В тАУ при одному пострiлi влучила друга гармата. Подii сумiснi i незалежнi, отже, подiю С (влучення у цiль при залпi), можна розглядати як суму двох сумiсних подiй: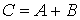
. За теоремою додавання отримаiмо:
.
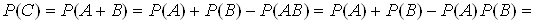
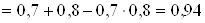Розглянемо другий спосiб розвтАЩязку.
Цiль буде вражена, якщо вiдбудеться одна з трьох несумiсних подiй:
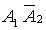ВатАУ влучила перша гармата i не влучила друга;
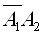ВатАУ не влучила перша гармата i влучила друга;
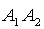ВатАУ влучили у цiль обидвi гармати.
У цьому випадку, застосувавши теореми про ймовiрностi суми i добутку подiй, отримаiмо:
.
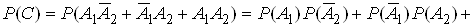
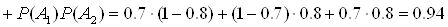Найпростiший розвтАЩязок задачi отримаiмо, якщо всi три несумiснi подii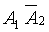 
, 
, 
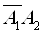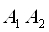Ваоб'iднаiмо в одну, сказавши "у цiль буде влучено, якщо влучить хоча б одна гармата" (подiя С).
Протилежна подiя: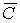 
ВатАУ в цiль не попала жодна з гармат. За теоремою про ймовiрнiсть протилежних подiй:
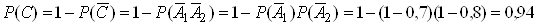
Приклад 2.
Студент прийшов на екзамен, знаючи 15 з 20 запитань програми. Знайти ймовiрнiсть того, що вiн знаi вiдповiдi на всi три запропонованi йому екзаменатором запитання.
РозвтАЩязок.
Подiя А (студент знаi вiдповiдi на всi три запитання) добутком трьох залежних подiй: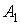 
Ва(знаi вiдповiдь на перше запитання), 
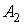Ва(знаi вiдповiдь на друге запитання) i 
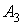Ва(знаi вiдповiдь на третi запитання).
Обчислимо ймовiрностi цих подiй:
.
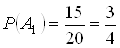За умови, що студент знаi вiдповiдь на перше запитання, ймовiрнiсть того, що знаi вiдповiдь надруге запитання:
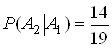Ва,
оскiльки запитання не повторюються i, якщо студент знаi вiдповiдь наперше запитання, то з 19 запитань, що залишилися, вiн знаi вiдповiдi лишена1
Припускаючи, що студент знаi вiдповiдi i на перше, i на друге запитання, обчислимо умовну ймовiрнiсть подii, яка полягаi в тому, що вiн знаi вiдповiдь натретi запитання:
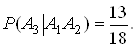
За теоремою множення маiмо:
.
Приклад 3.
З п'яти букв розрiзноi азбуки складене слово "КНИГА". Дитина, що не умiла читати, розсипала цi букви i потiм зiбрала iх в довiльному порядку. Знайти ймовiрнiсть того, що у неi знову вийшло слово "КНИГА".
РозвтАЩязок.
У попередньому роздiлi ця задача була вже розвтАЩязана. Наведемо другий можливий варiант розвтАЩязку. Щоб в порядку появи букв вийшло слово "КНИГА" першою повинна з'явитися буква К. Ймовiрнiсть цiii подii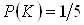 
Ва(iз заданих п'яти букв тiльки одна буква К). Припускаючи, що ця подiя сталася, знайдемо ймовiрнiсть того, що другою з'явиться буква Н: 
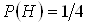. Припускаючи, що вiдбулися обидвi подii, тобто з'явилися букви К i Н обчислимо ймовiрнiсть появи наступноi букви 
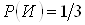. Аналогiчно 
, 
.
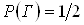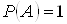За теоремою множення ймовiрностей залежних подiй отримаiмо шукану ймовiрнiсть:
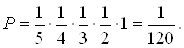
3. Формула повноi ймовiрностi. Формула Байiса
Нехай подiя Ваможе статися за умови появи однiii з несумiсних подiй (гiпотез) 
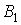Ва,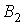
, .. ,
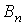, що створюють повну групу. Тодi ймовiрнiсть подii 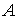Ваобчислюiться за формулою повноi ймовiрностi:
,
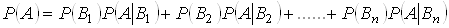
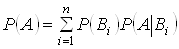де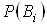 
ВатАУ ймовiрнiсть гiпотези 
; 
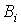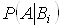ВатАУ умовна ймовiрнiсть подii 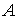Ваза умови, що подiя 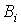Вавiдбулася.
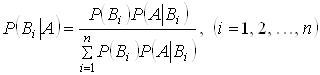
Якщо до експерименту ймовiрностi гiпотез були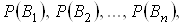 
Ваа внаслiдок експерименту вiдбулася подiя 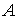, то з урахуванням цiii подii "новi", тобто умовнi, ймовiрностi гiпотез обчислюються за формулами Байiса:
.
Формули Байiса дають можливiсть "переглянути" ймовiрностi гiпотез з урахуванням результату експерименту, що спостерiгався.
Приклад.
На склад надходить продукцiя трьох фабрик, причому продукцiя першоi фабрики становить 20%, другоi тАУ 46%, третьоi тАУ 34%. Вiдомо також, що середнiй процент нестандартних деталей для першоi фабрики дорiвнюi 3%, другоi тАУ 2%, третьоi тАУ 1%.
1. Знайти ймовiрнiсть того, що вибрана навмання деталь буде нестандартною.
2. Знайти ймовiрнiсть того, що деталь виготовлена на першiй фабрицi, якщо вона виявилася нестандартною.
3. Знайти ймовiрнiсть того, що деталь виготовлена на другiй фабрицi, якщо вона виявилася стандартною.
РозвтАЩязок.
1. Вибрана навмання деталь може бути виготовлена або на першiй фабрицi (подiя 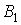) або на другiй (подiя 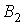) або на третiй (подiя 
). Подii несумiснi i складають повну групу. Ймовiрностi подiй данi в умовi задачi:
.
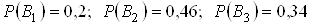В умовi заданi й умовнi ймовiрностi. Ймовiрнiсть того, що навмання вибрана деталь буде нестандартною (подiя 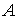) за умови, що деталь виготовлена на першiй фабрицi (подiя ): 
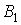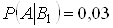. Аналогiчно, 
; 
.
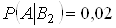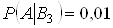Подiя 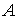Ва(навмання вибрана деталь буде нестандартною) може вiдбутися тiльки разом з однiiю з несумiсних подiй з повноi групи, тому повну ймовiрнiсть подii 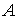Вавизначимо за формулою повноi ймовiрностi:
.
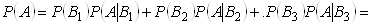
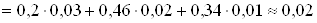2. Вiдомо, що подiя 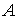Вавже вiдбулася, потрiбно знайти пiслядослiдну ймовiрнiсть гiпотези 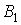. За формулою Байiса знаходимо:
.
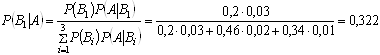3. Деталь виявилася стандартною, тобто в прийнятих нами позначеннях вiдбулася подiя 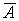. Знайти пiслядослiдну ймовiрнiсть подii 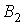. За формулою Байiса:
Подii 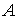Ва(навмання вибрана деталь тАУ нестандартна), 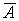Ва(навмання вибрана деталь тАУ стандартна) протилежнi, тому
.
Аналогiчно обчислюiться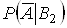 
:
.
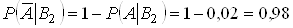Пiдставляючи обчисленi значення у формулу, отримаiмо:
.
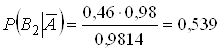Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы