Паралельнi проекцii

Лабораторна №3

Паралельнi проекцii

Метою раздiлу i ознайомлення з елементарним математичним апаратом плоских геометричних проекцiй. Для простоти будемо вважати, що при центральному проектуваннi картинна площина перпендикулярна осi z i збiгаiться з площиною z = d, а при паралельному збiгаiться з площиною z = 0. Проекцii розглядаються в системi координат спостерiгача, що i лiвосторонньою. Система координат, в якiй вiсь х спрямована вправо, вiсь у - вгору, а вiсь z - усередину екрана, природньо погоджуiться з екраном дисплея.

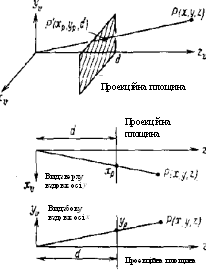
Рис.1 Центральна проекцiя

Кожну з проекцiй можна описати матрицею розмiром 4х4. Цей спосiб виявляiться зручним, оскiльки з'являiться можливiсть об'iднати матрицю проектування з матрицею перетворення, представивши в результатi двi операцii (перетворення i проектування) у видi однiii матрицi. У цьому роздiлi ми одержимо матрицi розмiром 4х4 для декiлькох проекцiй i насамперед для центральноi. На рис.1 наведенi три зображення лiвосторонньоi системи координат, у яких точка P проектуiться на проекцiйну площину, розташовану на вiдстанi d вiд початку координат. Для обчислення координат Xр i Yp проекцii точки (x, у, z) напишемо спiввiдношения, отриманi з подiбностi трикутникiв (рис.1):

Перемножуючи обидвi сторони кожного спiввiдношення на d, одержимо

Вiдстань d i в даному випадку масштабним множником, застосованим до координат Xp i Yp. Фактором, що приводить до того, що на центральнiй проекцii бiльш вiддаленi об'iкти виглядають дрiбнiше, нiж ближчi, i дiлення на z. Вiдзначимо, що допустимi всi значення z, крiм z = 0. Точки можуть розташовуватися як за центром проекцii на вiдтАЩiмнiй частинi осi z, так i мiж центром проекцii i проекцiйною площиною.

Цi перетворення можна представити у виглядi матрицi розмiром 4х4:

Множачи точку Вана матрицю . отримаiмо загальний вираз для точки в однорiдних координатах :

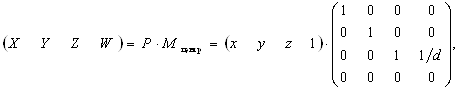
геометричний проекцiя косокутний матриця

Тепер, подiливши на W (що дорiвнюi z/d) для зворотнього переходу до трьох вимiрiв, отримаiмо

Цей результат i коректним, оскiльки мiстить перетворену z - координату з 1, що вiдповiдаi положенню проекцiйноi ПЛОЩИНИ ВЗДОВЖ ОСРЖ 2.

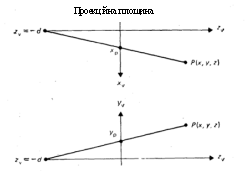
Рис. 2 РЖнша схема побудови центральноi проекцii

При iншому представленнi центрального проектування, застосовуваному в деяких роботах, проекцiйна площина сполучаiться з площиною 2 = 0, а центр проекцii розташовуiться в точцi 2 = - с (рис. 2). З подiбностi трикутникiв випливаi

Звiдси одержуiмо

Матриця записуiться у видi

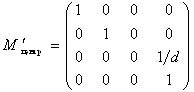
Цю матрицю можна одержати з матрицi Вашляхом переносу центра проекцii в початок координат, застосування Ваi зворотнього переносу:

Ортографiчне проектування на площину z = 0 очевидне. Напрямок проектування збiгаiться з нормаллю до площини проекцii, тобто в нашому випадку з вiссю z. Таким чином, точка Р маi координати:

Ця проекцiя описуiться матрицею

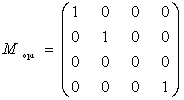
Рис. 3 Косокутна рiвнобiжна проекцiя одиничного куба.

Точка Р' i проекцiiю точки P (0, 0, 1)

Розглянемо тепер косокутну проекцiю, матриця якоi може бути записана виходячи зi значень a i l (рис. 3). На рис. 3 зображений одиничний куб, спроектований на xy-площину. З малюнка видно, що проекцiiю точки P (0, 0, 1), що знаходиться на заднiй сторонi' одиничного куба, i точка Р'(l соsа, l sinа, 0), що належить площинi ху. По визначенню це означаi, що напрям проектування збiгаiться з вiдрiзком РР', що проходить через цi двi точки (рис. 4). Цей напрям i Р'-Р= (l соsа, l sina, -1). Напрям проектування складаi кут р iз площиною ху.

Тепер розглянемо довiльну точку x, у, z i визначимо ii косокутну проекцiю (Хр,Ур) на площину ху. На рис. 5 показанi два зображення точки i проектор, що рiвнобiжний проектору, приведеному на рис.4. Рiвняння для x- i y-координат проектора як функцiй z мають вид у=mz+b. Вирiшуючи два рiвняння относительно Хр i Yр, вiдзначених на рис.5, одержуiмо

Матриця розмiром 4х4, що виконуi цi дii i, отже, описуi косокутну проекцiю, маi вигляд

Застосування матрицi Ваприведе до зсуву i наступного проектування об'iкта: площини з постiйною координатою z = z1 переносяться в напрямку х на z1*l соsa в напрямку y на z1*l sina i потiм проектуються на площину z = 0. Зсув зберiгаi паралельнiсть прямих, а також кути i вiдстанi в площинах, паралельних осi z.

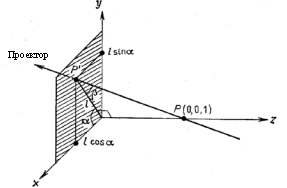
Рис. 4. Косокутна паралельна проекцiя Р'(l соsа, l sinа, 0) Вапроекцiiю точки P (0, 0, 1).

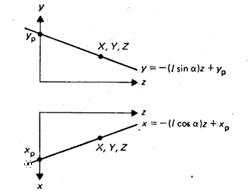
Рис. 5 Косокутна паралельна проекцiя (Xp, Yp, 0) точки (x, y, z).

Для проекцii кавальi l=1, тому кут р, показаний на рис.4.17, складаi 45В°. Для проекцii кабiнi l=1/2, а b=агtg (2) =63,4В°. У випадку ортографiчноi проекцii l = 0 i b = 90В°, тому Ваi окремим випадком .

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы