Подвiйний iнтеграл

ПОДВРЖЙНИЙ РЖНТЕГРАЛ

Содержание

1. Задачi, що приводять до поняття подвiйного iнтеграла

Задача про об'iм цилiндричного тiла

Задача про масу пластини

2. Поняття подвiйного iнтеграла. Умови його iснування та властивостi

3. Обчислення подвiйного iнтеграла

1. Задачi, що приводять до поняття подвiйного iнтеграла
Задача про об'iм цилiндричного тiла

Нехай маiмо тiло, обмежене зверху поверхнею 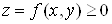, знизу - замкненою обмеженою областю Ваплощини , з бокiв - цилiндричною поверхнею, напрямна якоi збiгаiться з межею областi , а твiрнi паралельнi осi Ва(рис.1). Таке тiло називають цилiндричним.

Обчислимо його об'iм . Для цього довiльним способом розiб'iмо область Вана 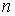Вачастин 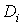, якi не мають спiльних внутрiшнiх точок, i площi яких дорiвнюють , 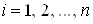. У кожнiй областi 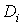Вавиберемо довiльну точку 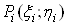, знайдемо значення функцii в цiй точцi 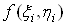Ваi обчислимо добуток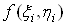 . Цей добуток дорiвнюi об'iму цилiндричного стовпчика з твiрними, паралельними осi , основою 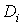Ваi висотою 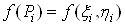. Усього таких стовпчикiв i 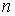, i сума iхнiх об'iмiв

Ва(1)

наближено дорiвнюi об'iму цилiндричного тiла . Це наближення тим точнiше, чим бiльше число 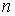Ваi чим меншi розмiри областей 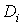. Назвемо дiаметром 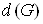Вазамкненоi обмеженоi областi 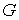Ванайбiльшу вiдстань мiж двома точками межi цiii областi. Позначимо через 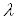Ванайбiльший з дiаметрiв областей 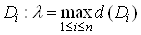. Тодi природно об'iм даного тiла визначити як границю суми (1) при :

. (2)

Задача про масу пластини

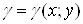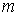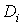Нехай маiмо плоску неоднорiдну матерiальну пластину, формою якоi i область Ва(рис.2). В областi Вазадана неперервна функцiя , яка визначаi густину пластини в точцi . Знайдемо масу Вапластини. Для цього довiльним способом розiб'iмо область Вана частини , якi не мають спiльних внутрiшнiх точок, i площi яких дорiвнюють , .

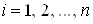У кожнiй областi 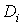Вавiзьмемо будь-яку точку 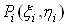Ваi знайдемо густину в цiй точцi:

.

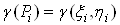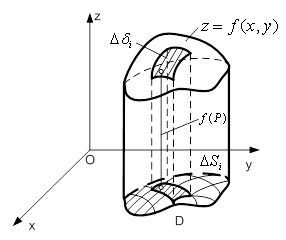
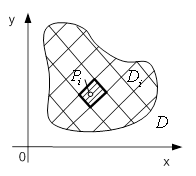
Рисунок 1 - Цилiндричне тiлоВаВаВаВаВаВа Рисунок 2 - Матерiальна пластина

Якщо розмiри областi Вадостатньо малi, то густина в кожнiй точцi Вамало вiдрiзнятиметься вiд значення . Тодi добуток Ванаближено визначаi масу тiii частини пластини, яка займаi область 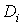, а сума

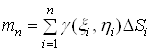Ва(3)

i наближеним значенням маси 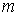Вавсiii пластини. Точне значення маси отримаiмо як границю суми (3) при :

. (4)

Таким чином, рiзнi за змiстом задачi ми звели до знаходження границь (2) i (4) одного й того самого виду. Можна навести ще ряд задач з фiзики i технiки, розв'язання яких призводить до обчислення подiбних границь. У зв'язку з цим виникаi потреба у вивченнi властивостей цих границь, незалежно вiд змiсту тiii чи iншоi задачi. Кожна така границя називаiться подвiйним iнтегралом. Дамо точнi означення.

2. Поняття подвiйного iнтеграла. Умови його iснування та властивостi

Нехай функцiя 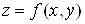Вавизначена в замкненiй обмеженiй областi . Вважатимемо, що межа областi Васкладаiться iз скiнченного числа неперервних кривих, кожна з яких визначаiться функцiiю виду 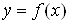Ваабо 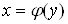. Розiб'iмо область Вана 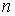Вачастини 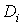, якi не мають спiльних внутрiшнiх точок i площi яких дорiвнюють , 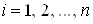. У кожнiй областi 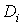Вавiзьмемо довiльну точку 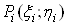i утворимо суму

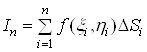, (5)

яку назвемо iнтегральною сумою для функцii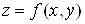 за областю . Нехай 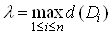Ва- найбiльший з дiаметрiв областей 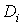. Якщо iнтегральна сума (5) при Вамаi скiнченну границю, яка не залежить нi вiд способу розбиття областi Вана частиннi областi 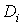, нi вiд вибору точок 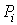Вав них, то ця границя називаiться подвiйним iнтегралом i позначаiться одним iз таких символiв:

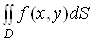Ваабо .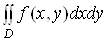

Таким чином, за означенням

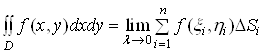. (6)

У цьому випадку функцiя 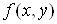Ваназиваiться iнтегровною в областi;

Ва- областю iнтегрування; 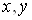Ва- змiнними iнтегрування; 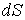Ва(або 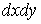) - елементом площi.

Звернемося до задач п. Якщо границi в рiвностях (2) i (4) iснують, то з цих рiвностей i формули (6) отримуiмо формули для обчислення об'iму цилiндричного тiла

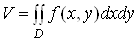Ва(7)

та маси пластинки

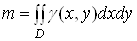. (8)

Якщо у формулi (7) покласти 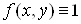, , 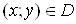то отримаiмо формулу для обчислення площi Ваобластi :

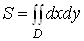. (9)

Рiвностi (7) i (8) розглядають вiдповiдно як геометричний та механiчний змiст подвiйного iнтеграла, якщо пiдiнтегральна функцiя невiд'iмна в областi.

Теорема (достатня умова iнтегровностi функцii). Якщо функцiя 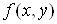Ванеперервна в замкненiй обмеженiй областi, то вона iнтегровна в цiй областi.

РД ще й iншi умови iснування подвiйного iнтеграла, але надалi ми вважатимемо, що пiдiнтегральна функцiя 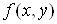Вав областi iнтегрування Ваi неперервною.

Порiвнюючи означення подвiйного iнтеграла (6) та означення визначеного iнтеграла

,

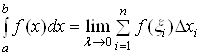бачимо, що конструктивно цi означення цiлком аналогiчнi: в обох випадках розглядаiться деяка функцiя 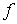, але в першому випадку це функцiя однiii змiнноi, визначена на одновимiрнiй областi - вiдрiзку 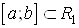, а в другому - це функцiя двох змiнних, визначена у двовимiрнiй областi. В обох випадках область визначення розбиваiться на частини, в кожнiй з яких береться довiльна точка i в нiй знаходиться значення функцii. Пiсля цього знайдене значення функцii множиться на мiру вiдповiдноi частини областi визначення. У випадку однiii змiнноi такою мiрою була довжина 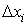Вавiдрiзка 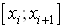, а у випадку двох змiнних - площа Ваобластi 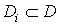. Наступнi кроки знову однаковi: утворюються iнтегральнi суми i знаходяться iхнi границi, коли мiра частин областi визначення прямуi до нуля. Пiзнiше ми побачимо, що за цiiю самою схемою будуiться i потрiйний iнтеграл, тiльки мiрою областi там i об'iм.

У зв'язку з цим, властивостi подвiйного iнтеграла аналогiчнi вiдповiдним властивостям визначеного iнтеграла. Сформулюiмо цi властивостi.

Сталий множник можна винести за знак подвiйного iнтеграла:

, .

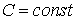Подвiйний iнтеграл вiд суми двох функцiй дорiвнюi сумi подвiйних iнтегралiв вiд цих функцiй:

.

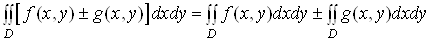Ця властивiсть маi мiсце для суми довiльного скiнченного числа функцiй.

Якщо в областi Вафункцiя, то

.

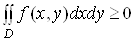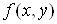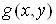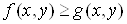Якщо функцii Ваi Вавизначенi в однiй i тiй самiй областi Ваi , то

.

(Адитивнiсть подвiйного iнтеграла). Якщо область iнтегрування функцii 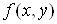Варозбити на област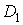i Ваi 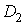, якi не мають спiльних внутрiшнiх точок, то

.

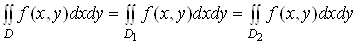Ця властивiсть називаiться адитивнiстю подвiйного iнтеграла i справедлива для довiльного скiнченого числа областей, якi складають область Ваi не мають спiльних внутрiшнiх точок.

(Оцiнка подвiйного iнтеграла). Якщо функцiя неперервна в обмеженiй замкненiй областi , яка маi площу , то

,

де 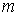Ваi 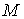Ва- вiдповiдно найменше i найбiльше значення пiдiнтегральноi функцii в областi .

(Середнi значення функцii.) Якщо функцiя 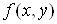Ванеперервна в замкненiй обмеженiй областi , яка маi площу , то в цiй областi iснуi така точка Ващо

.

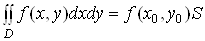Величину

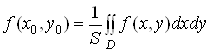
називають середнiм значенням функцii 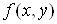Вав областi .

подвiйний iнтеграл адитивнiсть

3. Обчислення подвiйного iнтеграла

Обчислення подвiйного iнтеграла за формулою (6) як границi iнтегральноi суми, так само як i у випадку визначеного iнтеграла, пов'язане iз значними труднощами. Щоб уникнути iх, обчислення подвiйного iнтеграла зводять до обчислення так званого повторного iнтеграла - двох звичайних визначених iнтегралiв.

Покажемо, як це робиться. Припустимо, що при 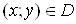Вафункцiя . Тодi, згiдно з формулою (7), подвiйний iнтеграл виражаi об'iм цилiндричного тiла (рис.3) з основою , обмеженого зверху поверхнею 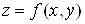. Обчислимо цей об'iм за допомогою методу паралельних перерiзiв [6]:

,

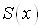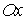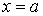де Ва- площа перерiзу тiла площиною, перпендикулярною до осi , а Вата 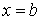Ва- рiвняння площин, якi обмежують дане тiло. Перед тим, як обчислювати площу зробимо певнi припущення вiдносно областi .

Припустимо спочатку, що область iнтегрування Ваобмежена двома неперервними кривими 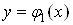Вата 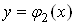Ваi двома прямими 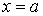Вата 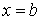, причому 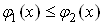Вадля всiх 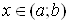Ва(рис.4). Проведемо через точку 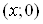, де 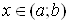, пряму, паралельну осi . Ця пряма перетинаi кривi 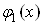та 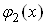Вав точках 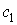Ваi 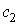, якi називатимемо вiдповiдно точкою входу в область Ваi точкою виходу з областi . Ординати цих точок позначимо вiдповiдно 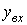Вата 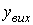, тодi , .

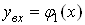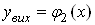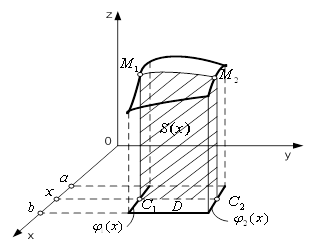
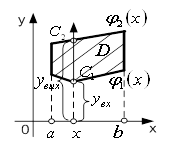
Рисунок 3 - Цилiндричне тiлоВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Рисунок 4 - Область

Визначена таким чином область називаiться правильною в напрямi осi . РЖнакше кажучи, область Ваназиваiться правильною в напрямi осi , якщо довiльна пряма, яка проходить через внутрiшню точку областi Вапаралельно осi , перетинаi межу областi не бiльше, нiж у двох точках.

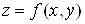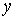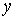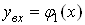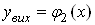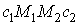Знайдемо тепер площу . Для цього проведемо через точку Ваплощину, перпендикулярну осi Ва(рис.3). У перерiзi цiii площини i цилiндричного тiла утворюiться трапецiя . Аплiката Ваточки лiнii Вапри фiксованому Ваi функцiiю лише , причому Вазмiнюiться в межах вiд Вадо . Площа Ватрапецii Вадорiвнюi визначеному iнтегралу

.

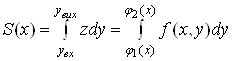Пiдставивши знайдене значення у формулу Ваi враховуючи формулу (7), отримаiмо

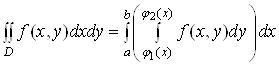
або в зручнiшiй формi

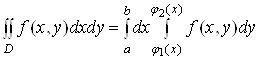. (10)

Це i i шукана формула для обчислення подвiйного iнтеграла. Праву частину формули (10) називають повторним iнтегралом вiд функцii 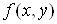Ваза областю. У повторному iнтегралi (10) iнтегрування виконуiться спочатку за змiнною 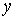Ва(при цьому Вавважаiться сталою), а потiм за змiнною . РЖнтеграл за змiнною 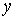Ваназивають внутрiшнiм, а за змiнною Ва- зовнiшнiм. 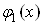У результатi обчислення внутрiшнього iнтеграла (в межах вiд Вадо 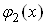) одержуiмо певну функцiю вiд однiii змiнноi . 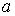РЖнтегруючи цю функцiю в межах вiд Вадо 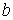, тобто обчислюючи зовнiшнiй iнтеграл, отримаiмо деяке число - значення подвiйного iнтеграла. Зауваження Наведенi геометричнi мiркування при одержаннi формули (10) можливi у випадку, коли 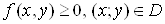. Проте формула (10) залишаiться справедливою i в загальному випадку. Зауваження 2. 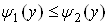Якщо область Ваобмежена двома неперервними кривими i двома прямими Вапричому Вадля всiх 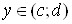, тобто якщо область Ваправильна в напрямi осi 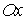Ва(рис.5), то справедлива формула

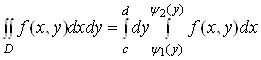. (11)

Тут внутрiшнiм i iнтеграл за змiнною . Обчислюючи його в межах вiд 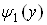до 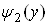Ва(при цьому 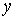Вавважаiться сталою), отримаiмо деяку функцiю вiд однiii змiнноi 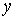. РЖнтегруючи потiм цю функцiю в межах вiд 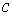Вадо 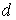, отримаiмо значення подвiйного iнтеграла.

Зауваження 3. Якщо область Ваправильна в обох напрямах, то подвiйний iнтеграл можна обчислювати як за формулою (10), так i за формулою (11). Результати матимемо однаковi.

Зауваження 4. Якщо область Ване i правильною нi в напрямi осi 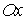, нi в напрямi осi Ва(тобто iснують вертикальнi i горизонтальнi прямi, якi, проходячи через внутрiшнi точки областi, перетинають ii межу бiльше, нiж у двох точках), то таку область необхiдно розбити на частини, кожна з яких i правильною областю у напрямi 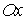Вачи . Обчислюючи подвiйнi iнтеграли по правильних областях i додаючи результати (властивiсть адитивностi), знаходимо шуканий подвiйний iнтеграл за областю . Для випадку, зображеного на рис.6 (область Ваобмежена елiпсами Ваi прямою 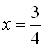), при iнтегруваннi в напрямi осi маiмо

.

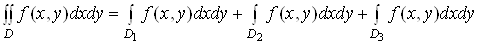У напрямi осi 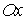Ватут потрiбно було б обчислити повторнi iнтеграли по семи областях.

Зауваження 5. Повторнi iнтеграли в правих частинах формули (10) i (11) називаються iнтегралами з рiзним порядком iнтегрування. Щоб змiнити порядок iнтегрування, потрiбно вiд формули (10) перейти до формули (11) або навпаки.

У кожному конкретному випадку, залежно вiд виду областi Вата пiдiнтегральноi функцii 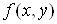, потрiбно обирати той порядок iнтегрування, який призводить до простiших обчислень.

Зауваження 6. Правильну в напрямi осi Ваобласть Вакоротко позначатимемо так:

.

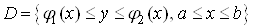Аналогiчно

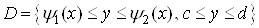
область правильна в напрямi осi .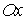

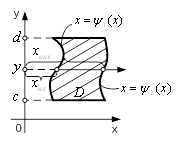
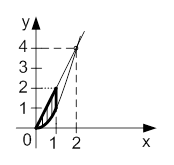
Рисунок 5 - Область ВаРисунок 6 - Область ВаРисунок 7 - Область

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы