Потрiйний iнтеграл
ПОТРРЖЙНИЙ РЖНТЕГРАЛ
1. Поняття потрiйного iнтеграла. Умови його iснування та властивостi
Схема побудови потрiйного iнтеграла така сама, як i звичайного визначеного iнтеграла та подвiйного iнтеграла.
Нехай функцiя ![]() Вавизначена в обмеженiй замкненiй областi
Вавизначена в обмеженiй замкненiй областi ![]() . Розiб'iмо область
. Розiб'iмо область ![]() Васiткою поверхонь на
Васiткою поверхонь на ![]() Вачастин
Вачастин ![]() , якi не мають спiльних внутрiшнiх точок i об'iми яких дорiвнюють
, якi не мають спiльних внутрiшнiх точок i об'iми яких дорiвнюють ![]() . У кожнiй частинi
. У кожнiй частинi ![]() Вавiзьмемо довiльну точку
Вавiзьмемо довiльну точку ![]() Ваi утворимо суму
Ваi утворимо суму
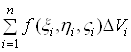 ,(1)
,(1)
яка називаiться iнтегральною сумою для функцii ![]() Ваза областю
Ваза областю ![]() . Нехай
. Нехай ![]() ВатАУ найбiльший з дiаметрiв областей
ВатАУ найбiльший з дiаметрiв областей ![]() .
.
Якщо iнтегральна сума (1) при ![]() Вамаi скiнченну границю, яка не залежить нi вiд способу розбиття областi
Вамаi скiнченну границю, яка не залежить нi вiд способу розбиття областi ![]() Вана частини
Вана частини ![]() , нi вiд вибору в них точок
, нi вiд вибору в них точок ![]() , то ця границя називаiться потрiйним iнтегралом i позначаiться одним iз таких символiв:
, то ця границя називаiться потрiйним iнтегралом i позначаiться одним iз таких символiв:
![]() Ваабо
Ваабо ![]() .
.
Таким чином, за означенням
 ,(2)
,(2)
де ![]() ВатАУ функцiя, iнтегровна в областi
ВатАУ функцiя, iнтегровна в областi ![]() ;
; ![]() ВатАУ область iнтегрування;
ВатАУ область iнтегрування; ![]() Ваi
Ваi ![]() тАУ змiннi iнтегрування;
тАУ змiннi iнтегрування; ![]() Ва(або
Ва(або ![]() ) тАУ елемент об'iму.
) тАУ елемент об'iму.
Якщо по тiлу ![]() Варозподiлено масу з об'iмною густиною
Варозподiлено масу з об'iмною густиною ![]() Вав точцi
Вав точцi ![]() , то маса
, то маса ![]() Вацього тiла знаходиться за формулою
Вацього тiла знаходиться за формулою
![]() . (3)
. (3)
Формула (3) аналогiчна формулi (1.8) i може розглядатися як механiчний змiст потрiйного iнтеграла, коли пiдiнтегральна функцiя невiд'iмна в областi ![]() . Якщо всюди в областi покласти
. Якщо всюди в областi покласти ![]() , то з формули (2) випливаi формула для обчислення об'iму
, то з формули (2) випливаi формула для обчислення об'iму ![]() Ватiла
Ватiла ![]() :
:
![]() .(4)
.(4)
Потрiйний iнтеграл i безпосереднiм узагальненням подвiйного iнтеграла на тривимiрний простiр. Теорiя потрiйного iнтеграла аналогiчна теорii подвiйного iнтеграла, тому в бiльшостi випадкiв ми обмежимося лише формулюваннями тверджень i короткими поясненнями.
Теорема (достатня умова iнтегровностi функцii). Якщо функцiя ![]() Ванеперервна в обмеженiй замкненiй областi
Ванеперервна в обмеженiй замкненiй областi ![]() , то вона в цiй областi iнтегрована.
, то вона в цiй областi iнтегрована.
Властивостi потрiйних iнтегралiв.
1. Сталий множник можна винести за знак потрiйного iнтеграла:
![]() .
.
Потрiйний iнтеграл вiд суми кiлькох iнтегровних функцiй дорiвнюi сумi потрiйних iнтегралiв вiд доданкiв:
![]() .
.
3. Якщо в областi iнтегрування ![]() , то
, то
![]() .
.
4. Якщо функцii ![]() Вата
Вата ![]() Вавизначенi в однiй i тiй самiй областi
Вавизначенi в однiй i тiй самiй областi ![]() Ваi
Ваi ![]() , то
, то
![]() .
.
5. (Адитивнiсть потрiйного iнтеграла.) Якщо область iнтегрування ![]() Вафункцii
Вафункцii ![]() Варозбити на частини
Варозбити на частини ![]() Ваi
Ваi ![]() , якi не мають спiльних внутрiшнiх точок, то
, якi не мають спiльних внутрiшнiх точок, то
![]() .
.
6. (Оцiнка потрiйного iнтеграла.) Якщо функцiя ![]() Ванеперервна в обмеженiй замкненiй областi
Ванеперервна в обмеженiй замкненiй областi ![]() , яка маi об'iм
, яка маi об'iм ![]() , то
, то
![]() ,
,
де ![]() Ваi
Ваi ![]() Вавiдповiдно найменше i найбiльше значення функцii
Вавiдповiдно найменше i найбiльше значення функцii ![]() Вав областi
Вав областi ![]() .
.
7. (Середнi значення функцii.) Якщо функцiя ![]() Ванеперервна в обмеженiй замкненiй областi
Ванеперервна в обмеженiй замкненiй областi ![]() , яка маi об'iм
, яка маi об'iм ![]() , то в цiй областi iснуi така точка
, то в цiй областi iснуi така точка ![]() , що
, що
![]() .
.
Величина
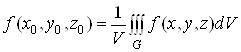
називаiться середнiм значенням функцii ![]() Вав областi
Вав областi ![]() .
.
2. Обчислення потрiйного iнтеграла
Обчислення потрiйного iнтеграла зводять до обчислення повторних, тобто до iнтегрування за кожною змiннiй окремо.
Нехай область ![]() Ваобмежена знизу i зверху поверхнями
Ваобмежена знизу i зверху поверхнями ![]() Ваi
Ваi ![]() , а з бокiв цилiндричною поверхнею, твiрнi якоi паралельнi осi
, а з бокiв цилiндричною поверхнею, твiрнi якоi паралельнi осi ![]() . Позначимо проекцiю областi
. Позначимо проекцiю областi ![]() Вана площину
Вана площину ![]() Вачерез
Вачерез ![]() Ва(рис. 1) i вважатимемо, що функцii
Ва(рис. 1) i вважатимемо, що функцii ![]() Ваi
Ваi ![]() Ванеперервнi в
Ванеперервнi в ![]() .
.
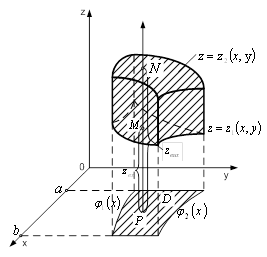
Рисунок 1 тАУ Область ![]()
Якщо при цьому область ![]() Ваi правильною, то область
Ваi правильною, то область ![]() Ваназиваiться правильною у напрямi осi
Ваназиваiться правильною у напрямi осi ![]() . Припустимо, що кожна пряма, яка проходить через кожну внутрiшню точку
. Припустимо, що кожна пряма, яка проходить через кожну внутрiшню точку ![]() Вапаралельно осi
Вапаралельно осi ![]() , перетинаi межу областi
, перетинаi межу областi ![]() Вау точках
Вау точках ![]() Ваi
Ваi ![]() . Точку
. Точку ![]() Ваназвемо точкою входу в область
Ваназвемо точкою входу в область ![]()
![]() , а точку
, а точку ![]() ВатАУ точкою виходу з областi
ВатАУ точкою виходу з областi ![]() , а iхнi аплiкати позначимо вiдповiдно через
, а iхнi аплiкати позначимо вiдповiдно через ![]() Ваi
Ваi ![]() . Тодi
. Тодi ![]() ,
, ![]() Ваi для будь-якоi неперервноi в областi
Ваi для будь-якоi неперервноi в областi ![]() Вафункцii
Вафункцii ![]() Вамаi мiсце формула
Вамаi мiсце формула
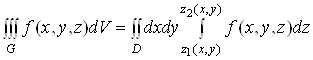 .(5)
.(5)
Змiст формули (5) такий. Щоб обчислити потрiйний iнтеграл, потрiбно спочатку обчислити iнтеграл  Ваза змiнною
Ваза змiнною ![]() , вважаючи
, вважаючи ![]() Вата
Вата ![]() Васталими. Нижньою межею цього iнтеграла i аплiката точки
Васталими. Нижньою межею цього iнтеграла i аплiката точки ![]() Вавходу
Вавходу ![]() , а верхньою тАУ аплiката
, а верхньою тАУ аплiката ![]() точки виходу
точки виходу ![]() . Внаслiдок iнтегрування отримаiмо функцiю
. Внаслiдок iнтегрування отримаiмо функцiю ![]() Вавiд змiнних
Вавiд змiнних ![]() Вата
Вата ![]() .
.
Якщо область ![]() , наприклад, обмежена кривими
, наприклад, обмежена кривими ![]() Ваi
Ваi ![]()
![]() , де
, де ![]() Ваi
Ваi ![]() ВатАУ неперервнi функцii, тобто
ВатАУ неперервнi функцii, тобто
![]() , то, переходячи вiд подвiйного iнтеграла
, то, переходячи вiд подвiйного iнтеграла ![]() Вадо повторного (п. 1.3), отримаiмо формулу
Вадо повторного (п. 1.3), отримаiмо формулу
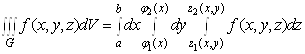 ,(6)
,(6)
яка зводить обчислення потрiйного iнтеграла до послiдовного обчислення трьох визначених iнтегралiв. Порядок iнтегрування може бути й iншим, тобто змiннi ![]() Ваi
Ваi ![]() Вау правiй частинi формули (6) за певних умов можна мiняти мiсцями.
Вау правiй частинi формули (6) за певних умов можна мiняти мiсцями.
Якщо, наприклад, область ![]() Ваправильна в напрямi осi
Ваправильна в напрямi осi ![]() :
:
![]() ,
,
де ![]() ВатАУ неперервнi функцii, то
ВатАУ неперервнi функцii, то
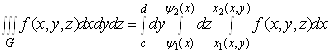 .
.
Зокрема, якщо областю iнтегрування i паралелепiпед:
![]() ,
,
то
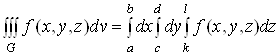 . (7)
. (7)
У цьому разi iнтегрування виконуiться в будь-якому порядку, оскiльки область ![]() Ваправильна у напрямi всiх трьох координатних осей
Ваправильна у напрямi всiх трьох координатних осей ![]() .
.
3. Замiна змiнних в потрiйному iнтегралi
Замiну змiнноi в потрiйному iнтегралi виконують за таким правилом: якщо обмежена замкнена область ![]() Вавзаiмно однозначно вiдображуiться на область
Вавзаiмно однозначно вiдображуiться на область ![]() Ваза допомогою неперервно диференцiйовних функцiй
Ваза допомогою неперервно диференцiйовних функцiй ![]() ,
, ![]() ,
, ![]() , якобiан
, якобiан ![]() Вав областi
Вав областi ![]() Ване дорiвнюi нулю:
Ване дорiвнюi нулю:

i ![]() ВатАУ неперервна в
ВатАУ неперервна в ![]() , то справедлива формула
, то справедлива формула
![]() . (8)
. (8)
На практицi найуживанiшими i цилiндричнi та сферичнi координати. При переходi вiд прямокутних координат ![]() Вадо цилiндричних
Вадо цилiндричних ![]() Ва(рис.4, а), пов'язаних з
Ва(рис.4, а), пов'язаних з ![]() спiввiдношеннями
спiввiдношеннями
![]() ;
;
![]() ,
,
якобiан перетворення
 .
.
З формули (8) отримуiмо потрiйний iнтеграл у цилiндричних координатах:
![]() .(9)
.(9)
Назва Влцилiндричнi координатиВ» пов'язана з тим, що координатна поверхня ![]() Ваi цилiндром, прямолiнiйнi твiрнi якого паралельнi осi
Ваi цилiндром, прямолiнiйнi твiрнi якого паралельнi осi ![]() .
.
При переходi вiд прямокутних координат ![]() Вадо сферичних
Вадо сферичних ![]()
(рис. 4, б), якi пов'язанi з ![]() Ваформулами
Ваформулами
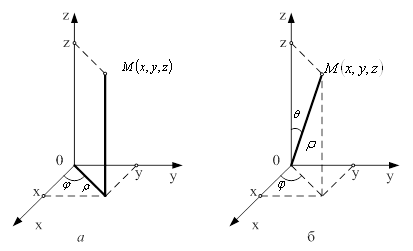
Рисунок 4 тАУ Координати: а) цилiндричнi; б) сферичнi
![]() ;
;
![]() ,
,
якобiан перетворення
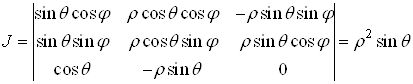 .
.
З формули (8) знаходимо потрiйний iнтеграл у сферичних координатах:
![]() . (10)
. (10)
Назва Влсферичнi координатиВ» пов'язана з тим, що координатна поверхня ![]() Ваi сферою. При обчисленнi потрiйного iнтеграла в цилiндричних чи сферичних координатах область
Ваi сферою. При обчисленнi потрiйного iнтеграла в цилiндричних чи сферичних координатах область ![]() , як правило, не будують, а межi iнтегрування знаходять безпосередньо за областю
, як правило, не будують, а межi iнтегрування знаходять безпосередньо за областю ![]() , користуючись геометричним змiстом нових координат. При цьому рiвняння поверхонь
, користуючись геометричним змiстом нових координат. При цьому рiвняння поверхонь ![]() Вата
Вата ![]() , якi обмежують область
, якi обмежують область ![]() , записують у нових координатах.
, записують у нових координатах.
Зокрема, якщо область ![]() Ваобмежена цилiндричною поверхнею
Ваобмежена цилiндричною поверхнею ![]() Вата площинами
Вата площинами ![]() , то всi межi iнтегрування в цилiндричнiй системi координат сталi:
, то всi межi iнтегрування в цилiндричнiй системi координат сталi:
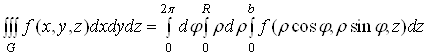
i не змiнюються при змiнi порядку iнтегрування. Те саме буде у сферичних координатах у випадку, коли ![]() ВатАУ куля:
ВатАУ куля: ![]() Ваабо кульове кiльце. Наприклад, якщо
Ваабо кульове кiльце. Наприклад, якщо ![]() ВатАУ кульове кiльце з внутрiшньою сферою
ВатАУ кульове кiльце з внутрiшньою сферою ![]() , то рiвняння цiii сфери в сферичних координатах маi вигляд
, то рiвняння цiii сфери в сферичних координатах маi вигляд
![]()
або
![]() ,
,
звiдки ![]() . Аналогiчно
. Аналогiчно ![]() ВатАУ рiвняння зовнiшньоi сфери, тому
ВатАУ рiвняння зовнiшньоi сфери, тому
![]() .
.
У випадку, коли ![]() ВатАУ куля
ВатАУ куля ![]() , у цiй формулi слiд покласти
, у цiй формулi слiд покласти ![]() . РЖнших будь-яких загальних рекомендацiй, коли необхiдно переходити до тiii чи iншоi системи координат, дати неможливо. Це залежить i вiд областi iнтегрування, i вiд пiдiнтегральноi функцii. РЖнодi потрiбно написати iнтеграл у рiзних системах координат i лише пiсля цього вирiшити, в якiй з них обчислення буде найпростiшим.
. РЖнших будь-яких загальних рекомендацiй, коли необхiдно переходити до тiii чи iншоi системи координат, дати неможливо. Це залежить i вiд областi iнтегрування, i вiд пiдiнтегральноi функцii. РЖнодi потрiбно написати iнтеграл у рiзних системах координат i лише пiсля цього вирiшити, в якiй з них обчислення буде найпростiшим.
Приклад
1. Обчислити iнтеграл ![]() , якщо область
, якщо область ![]() Ваобмежена поверхнями
Ваобмежена поверхнями ![]() Ваi
Ваi ![]() .
.
РозвтАЩязання
Область ![]() Ваi конусом (рис. 5).
Ваi конусом (рис. 5).

Рисунок 5 тАУ Область ![]()
Рiвняння конiчноi поверхнi, яка обмежуi область ![]() , можна записати у виглядi
, можна записати у виглядi ![]() , а саму область
, а саму область ![]() Ваподати таким чином:
Ваподати таким чином: ![]() , де
, де ![]() ВатАУ круг радiуса
ВатАУ круг радiуса ![]() Ваз центром
Ваз центром ![]() . Тому даний потрiйний iнтеграл можна звести до послiдовного обчислення трьох визначених iнтегралiв у прямокутних координатах:
. Тому даний потрiйний iнтеграл можна звести до послiдовного обчислення трьох визначених iнтегралiв у прямокутних координатах:
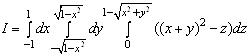 .
.
Проте зручнiше перейти до цилiндричних координат ![]() . Тодi прообраз круга
. Тодi прообраз круга ![]() Ваi прямокутник
Ваi прямокутник ![]() , прообраз конiчноi поверхнi тАУ плоска поверхня
, прообраз конiчноi поверхнi тАУ плоска поверхня ![]() , а прообраз областi
, а прообраз областi ![]() ВатАУ область
ВатАУ область ![]() . Якобiан переходу до цилiндричних координат дорiвнюi
. Якобiан переходу до цилiндричних координат дорiвнюi ![]() , пiдiнтегральна функцiя в цилiндричних координатах дорiвнюi
, пiдiнтегральна функцiя в цилiндричних координатах дорiвнюi![]() . Зводячи потрiйний iнтеграл за областю
. Зводячи потрiйний iнтеграл за областю ![]() Вадо послiдовного обчислення трьох визначних iнтегралiв, отримаiмо
Вадо послiдовного обчислення трьох визначних iнтегралiв, отримаiмо

![]()
Зазначимо, що розставлення меж iнтегрування в цилiндричних координатах, як правило, виконують, розглядаючи не область ![]() , а змiну цилiндричних координат в областi
, а змiну цилiндричних координат в областi ![]() . Наочно видно, що в областi
. Наочно видно, що в областi ![]() Вазмiнна
Вазмiнна ![]() Вазмiнюiться вiд
Вазмiнюiться вiд ![]() Вадо
Вадо ![]() , при кожному значеннi
, при кожному значеннi ![]() Вазмiнна
Вазмiнна ![]() Вазмiнюiться вiд
Вазмiнюiться вiд ![]() Вадо
Вадо ![]() , а для кожноi точки
, а для кожноi точки ![]() Ваобластi
Ваобластi ![]() Вазмiнна
Вазмiнна ![]() Вазмiнюiться в областi
Вазмiнюiться в областi ![]() Вавiд
Вавiд ![]() Ва(значення
Ва(значення ![]() Вав областi
Вав областi ![]() ) до
) до ![]() Ва(значення
Ва(значення ![]() Вана конiчнiй поверхнi).
Вана конiчнiй поверхнi).
4. Деякi застосування потрiйного iнтеграла
iнтеграл потрiйний обчислення змiнний
1. Обчислення об'iмiв. Якщо деяке тiло i обмеженою i замкненою
областю ![]() , що маi об'iм
, що маi об'iм ![]() , то згiдно з формулою (4)
, то згiдно з формулою (4)
![]() .(11)
.(11)
Застосування у механiцi. Нехай ![]() ВатАУ обмежена замкнена область простору
ВатАУ обмежена замкнена область простору ![]() , яку займаi деяке матерiальне тiло з густиною
, яку займаi деяке матерiальне тiло з густиною ![]() , де
, де ![]() ВатАУ неперервна функцiя в областi
ВатАУ неперервна функцiя в областi ![]() , тодi:
, тодi:
а)маса цього тiла
![]() ;(12)
;(12)
б)моменти iнерцii ![]() Ватiла вiдносно координатних осей
Ватiла вiдносно координатних осей ![]() Вавiдповiдно дорiвнюють
Вавiдповiдно дорiвнюють
![]() . (13)
. (13)
Моменти iнерцii ![]() Ватiла вiдносно координатних площин
Ватiла вiдносно координатних площин ![]() Ваобчислюються за формулами
Ваобчислюються за формулами
![]() .(14)
.(14)
Момент iнерцii тiла вiдносно початку координат
![]()
![]() (15)
(15)
в) статичнi моменти ![]() тiла вiдносно координатних площин
тiла вiдносно координатних площин ![]() Ваобчислюються за формулами
Ваобчислюються за формулами
![]() ;(16)
;(16)
г) координати ![]() Вацентра маси тiла визначаються за формулами
Вацентра маси тiла визначаються за формулами
 . (17)
. (17)
Доведення формули (11), як уже зазначалося, випливаi з означення потрiйного iнтеграла:
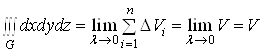 .
.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы