Системи лiнiйних рiвнянь

СИСТЕМИ ЛРЖНРЖЙНИХ РРЖВНЯНЬ

1. Основнi поняття i теореми

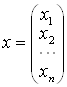
Постановка задачi. Потрiбно знайти значення х1, х2, тАж , хn , що задовольняють таким спiввiдношенням: .

Тут aij (i = 1, 2, тАж , m; j = 1, 2, тАж , ) i bk (k = 1, 2, тАж , m) тАУ заданi числа.

При цьому: ; ; .

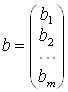
Матриця А називаiться головною матрицею системи, вектор тАУ вектором-стовпцем правих частин, вектор x тАУ вектором-стовпцем невiдомих.

Використовуючи цi позначки, можна систему записати в матричнiй формi: Ах = .

Якщо 1 = 2 = ¼ = bm = 0, то система рiвнянь називаiться однорiдною. Якщо хоча б одне з bk (k = 1, 2, ¼ , m) вiдмiнне вiд нуля, то система називаiться неоднорiдною.

.

Матриця Ваназиваiться розширеною матрицею системи.

Якщо система маi хоча б один розвтАЩязок, то вона називаiться сумiсною.

При цьому система, що маi iдиний розвтАЩязок, називаiться визначеною, а бiльше одного розвтАЩязку тАУ невизначеною.

Якщо система не маi розвтАЩязкiв, то вона називаiться несумiсною.

При розвтАЩязуваннi систем лiнiйних рiвнянь маi бути знайдена вiдповiдь на три запитання:

А. Чи сумiсна система?

В. Чи визначена система?

С. Як знайти розвтАЩязок (чи розвтАЩязки) системи, якщо вони iснують?

Правило Крамера. Якщо неоднорiдна система рiвнянь невироджена (detА ¹ 0), то система визначена, тобто маi iдиний розвтАЩязок, i його можна знайти за формулами Крамера: Ва(k = 1, 2, тАж , ) де Dk тАУ визначник матрицi, яку можна одержати, якщо в матрицi А системи k-й стовпець замiнити на стовпець вiльних членiв.

Ранг матрицi. З розвтАЩязуванням систем рiвнянь безпосередньо пов'язане поняття рангу матрицi. Ранг матрицi тАУ це найвищий порядок ii мiнора, вiдмiнного вiд нуля.

Для того щоб знайти ранг матрицi, важливо орiiнтуватися в тому, якi перетворення з матрицею можна робити, не змiнюючи при цьому ii ранг:

1) транспонування;

2) перестановка двох рядкiв (стовпцiв);

3) множення всiх елементiв рядка (або стовпця) на число a ¹ 0;

4) додавання до всiх елементiв рядка (стовпця) вiдповiдних елементiв iншого рядка (стовпця);

5) вилучення нульового рядка (стовпця);

6) викреслення рядка (стовпця), що i лiнiйною комбiнацiiю iнших рядкiв (стовпцiв).

Однорiднi системи. Розглядаiться однорiдна система лiнiйних рiвнянь з невiдомими: Ах = 0.

Якщо rangА = (detА ¹ 0), то система визначена i маi тiльки тривiальний розвтАЩязок: x1 = x2 = тАж = xn = 0.

Якщо rangА < (detА = 0), то система маi не тiльки тривiальнi розвтАЩязки. При цьому всi розвтАЩязки однорiдноi системи рiвнянь утворюють лiнiйний простiр L i dim L = тАУ rangА.

Щоб знайти базис простору розвтАЩязкiв однорiдноi системи рiвнянь, треба:

1.Знайти базисний мiнор матрицi А.

2.Якщо рядок не входить до базисного мiнора, то рiвняння, яке йому вiдповiдаi, i лiнiйною комбiнацiiю iнших рiвнянь, i його можна не брати до уваги.

3.Якщо стовпець не входить у базисний мiнор, то невiдома з вiдповiдним номером призначаiться вiльною. Усього знайдеться (тАУ rang A) вiльних невiдомих.

4.Нехай вiльнi невiдомi хr+1, хr+2, тАж , хn. Якщо дати вiльним невiдомим довiльнi значення, то одержимо неоднорiдну систему рiвнянь вiдносно хr+1, хr+2, тАж , х, у якоi визначник не дорiвнюi нулю, i, отже, система маi iдиний розвтАЩязок.

5.Дамо вiльним невiдомим значення (1, 0, 0, 0, тАж , 0), потiм (0, 1, 0, 0, тАж , 0) i т. д. РозвтАЩязуючи системи, що утворюють, одержимо вiдповiдно вектори . Цi вектори й утворюють базис простору L розвтАЩязкiв однорiдноi системи лiнiйних рiвнянь.

6.Загальний розвтАЩязок лiнiйноi системи однорiдних рiвнянь у цьому випадку i лiнiйною комбiнацiiю базисних векторiв:

.

Неоднорiднi системи. Теорема Кронекера тАУ Капеллi: система неоднорiдних лiнiйних рiвнянь Ах = сумiсна тодi i тiльки тодi, коли rangА = rang.

При цьому якщо rangА = rang= , то система маi iдиний розвтАЩязок i вiн може бути знайдений за правилом Крамера.

Якщо rangА = rang < , то система маi нескiнченно багато розвтАЩязкiв, якi утворюють лiнiйний многовид. При цьому пiдпростiр зсуву тАУ це простiр L розвтАЩязкiв однорiдноi системи рiвнянь, i його базис можна побудувати способом, який було розглянуто вище. Вектор зсуву тАУ це частинний розвтАЩязок неоднорiдноi системи рiвнянь. i вiн може бути знайдений, якщо в неоднорiднiй системi вiльнi невiдомi покласти рiвними деяким довiльним значенням (наприклад, нульовим).

Загальний розвтАЩязок неоднорiдноi системи тАУ це загальний розвтАЩязок вiдповiдноi однорiдноi системи плюс деякий частинний розвтАЩязок неоднорiдноi системи. Останнi твердження можна записати через абревiатури вiдповiдних термiнiв: З.Р.Н.С. = З.Р.О.С. + Ч.Р.Н.С.

Обернена матриця. Запишемо систему в матричному виглядi Ах = . Якщо detА ¹ 0 (така матриця А називаiться невиродженою), то для матрицi А iснуi матриця АтАУ1 така, що АтАУ1А = ААтАУ1 = Е.Така матриця називаiться оберненою до матрицi А, i розвтАЩязок системи можна записати за допомогою оберненоi матрицi у виглядi: АтАУ1Ах = АтАУ1Þ х = АтАУ1.

Таким чином, у випадку iснування оберненоi матрицi АтАУ1розвтАЩязок системи маi вигляд: х = АтАУ1.

Як же знайти обернену матрицю АтАУ1 до невиродженоi матрицi А?

I спосiб.

1) Складемо матрицю Аik з алгебраiчних доповнень до елементiв аik матрицi А;

2) транспонуiмо матрицю з алгебраiчних доповнень;

3) кожен елемент матрицi, що утворилась, дiлимо на detА.

В результатi маiмо обернену матрицю тАУ А-1.

II спосiб.

1) Запишемо матрицю А, а праворуч вiд неi, через вертикальну риску, тАУодиничну матрицю Е. Одержимо матрицю яка маi рядкiв та 2 стовпцiв;

2) у матрицi, що утворилась, за допомогою застосування до рядкiв (i тiльки до рядкiв) перетворень, що не змiнюють ранг матрицi, утворимо на мiсцi матрицi А одиничну матрицю.

На мiсцi одиничноi матрицi тепер стоiть АтАУ1.

III спосiб. Праворуч вiд матрицi припишемо одиничну матрицю Е, а знизу припишемо матрицю (тАУЕ). У правому нижньому кутi поставимо нульову матрицю. Використовуючи операцii тiльки над рядками матрицi, що утворилась, на мiсцi матрицi (тАУЕ) утворимо нульову матрицю. Тодi у правому нижньому кутi буде стояти АтАУ1.

IV спосiб. Для обернення матрицi, що маi блокову структуру, тобто матрицi вигляду: , де А тАУ квадратна матриця порядку ´ , а D тАУ квадратна матриця q ´ q, справедливi двi формули Фробенiуса:

1.Перша формула Фробенiуса (якщо detА ¹ 0):

, де H = D тАУ CAтАУ1B.

2.Друга формула Фробенiуса (якщо detD ¹ 0):

, де K = A тАУ BDтАУ1C.

2. Контрольнi питання i завдання

1. Що таке ранг матрицi i ii базисний мiнор? Чи визначаються вони однозначно?

1.2. Знайти ранг i всi базиснi мiнори матрицi: .

1.3. Як пов'язанi ранг матрицi i вимiрнiсть лiнiйноi оболонки ii рядкiв.

1.4. Чому дорiвнюi вимiрнiсть простору розвтАЩязкiв однорiдноi системи лiнiйних рiвнянь, якщо в системi 10 рiвнянь, 16 невiдомих i ранг матрицi системи дорiвнюi 6?

1.5. Чи утворюi множина розвтАЩязкiв неоднорiдноi системи лiнiйний простiр? Яка з властивостей лiнiйного простору не виконуiться?

1.6. Згадайте визначення лiнiйного многовиду. Що називаiться його базисом i вимiрнiстю?

1.7. Як визначаiться вектор зсуву для лiнiйного многовиду, що i множиною розвтАЩязкiв неоднорiдноi системи?

3. Приклади розвтАЩязування задач

Задача 1. Знайти ранг матрицi .

РозвтАЩязання. Насамперед вiдзначимо, що четвертий рядок матрицi i сумою другого i третього рядкiв i тому при вилученнi цього рядка ранг матрицi не змiниться.

1.Вiдкинемо четвертий рядок.

2.З другого i третього рядкiв матрицi вiднiмемо перший рядок, помножений, вiдповiдно, на 2 та 3.

3.В отриманiй матрицi з третього рядка вiднiмемо другий, помножений на 2.

Одержимо ланцюжок перетворень:

лiнiйний рiвняння матриця

.

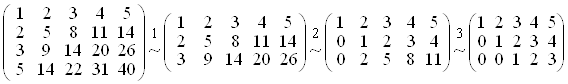У матрицi, що утворилась, мiнор, який стоiть в перших трьох стовпцях, не дорiвнюi нулю. Отже, ранг вихiдноi матрицi дорiвнюi 3 i мiнор 3-го порядку, що стоiть в перших трьох стовпцях, i базисним мiнором матрицi А.

Задача 2. Знайти матрицю, яка i оберненою до матрицi

.

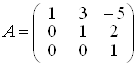РозвтАЩязання. Знайдемо обернену матрицю за визначенням. Нехай обернена матриця маi вигляд: . Тодi, за визначенням,

ААтАУ1 = Е, тобто .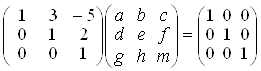

Знаходячи добуток матриць, одержимо рiвностi:

.

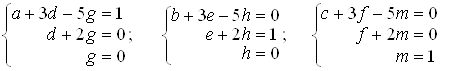РЖз цих спiввiдношень одержуiмо: g = 0, d = 0, a = 1; далi: h = 0, e =1, = тАУ3. РЖ нарештi: m = 1, f = тАУ2, c = 11. У пiдсумку дiйдемо висновку, що:

.

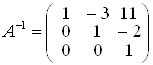Задача 3. Знайти матрицю, яка i оберненою до матрицi .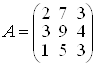

РозвтАЩязання. Побудуiмо матрицю 6 ´ 6, дописавши праворуч вiд А одиничну матрицю Е, внизу матрицю (тАУ Е), а iншi мiсця заповнимо нулями.

.

За допомогою операцiй над рядками матрицi А¢ утворимо на мiсцi (тАУЕ) нульову матрицю. Тодi в правому нижньому кутi буде стояти матриця АтАУ1.

1.До всiх рядкiв матрицi А¢ додамо третiй рядок з деяким множником, домагаючись того, щоб всi елементи першого стовпця, крiм а31, дорiвнювали нулю.

2.Перший рядок отриманоi матрицi подiлимо на (тАУ3) i, додаючи до iнших рядкiв матрицi отриманий перший рядок з деякими множниками, досягаiмо того, щоб у другому стовпцi стояли нулi, крiм елемента а12.

3.За допомогою другого рядка утворимо нулi в третьому стовпцi, крiм елемента а23.

Одержимо ланцюжок перетворень:

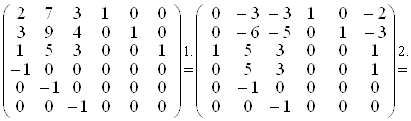
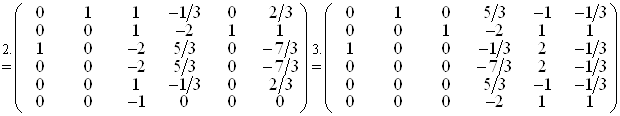
Звiдси укладаiмо, що .

Задача 4. Знайти матрицю, яка i оберненою до .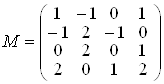

РозвтАЩязання. Для обернення матрицi застосуiмо першу формулу Фробенiуса. Позначимо: , , , .

Знаходимо послiдовно:

;

;

;

.

РЖ тодi 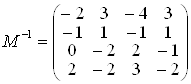. Привабливiсть зазначеного способу полягаi в тому, що для обернення матрицi 4-го порядку ми маiмо справу з оберненням матриць лише 2-го порядку, що iстотно простiше.

Задача 5. За допомогою правила Крамера розвтАЩязати систему лiнiйних неоднорiдних рiвнянь: .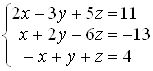

РозвтАЩязання. Головна матриця системи маi вигляд: .

РозвтАЩязок системи може бути знайдений за правилом Крамера, тому що detА = D = 18 ¹ 0. Для цього побудуiмо визначники Dх, Dу, Dz, якi вiдрiзняються вiд головного визначника тим, що в ньому стовпець коефiцiiнтiв при, вiдповiдно, х, у та z замiнено на стовпець вiльних членiв, тобто:

.

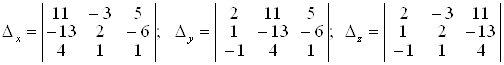Обчислюючи iх, знаходимо, що Dх = 18, Dу = 36, Dz = 54.

Отже .

Задача 6. РозвтАЩязати систему лiнiйних однорiдних рiвнянь:

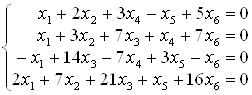
РозвтАЩязання. Насамперед вiдзначимо, що система напевне сумiсна, оскiльки однорiдна система завжди маi щонайменше нульовий розвтАЩязок.

Почнемо пошук загального розвтАЩязку даноi системи. Головна матриця системи маi вигляд: .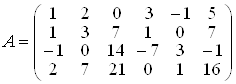

Знайдемо ранг матрицi А. Перший рядок матрицi з вiдповiдними множниками додамо до iнших рядкiв матрицi так, щоб елементи першого стовпця обернулися на нуль, крiм елемента а11. Вийде матриця А1 така, що

rangА1 = rangА i .

Вiдзначаючи, що третiй i четвертий рядки матрицi пропорцiйнi другому рядку, укладаiмо, що rangА1 = rangА2, де . Помножимо другий рядок матрицi А2 на (тАУ2) i додамо до першого рядка. Одержимо матрицю А3: , таку, що rangА3 = rangА2 = 2. У пiдсумку rangА = rangА3 = 2.

Тодi вийшла система двох рiвнянь, з яких можна написати:

х1 = 14х3 тАУ 7х4 + 3х5 тАУ х6, х2 = тАУ7х3 + 2х4 тАУ х5 тАУ 2х6 i змiннi х3, х4, х5, х6 тАУ будь-якi. Це i i розвтАЩязок системи.

Однак можна (i необхiдно) пiти далi. Множина розвтАЩязкiв лiнiйноi однорiдноi системи утворюi лiнiйний простiр L вимiрностi dimL = тАУ rangА = 6 тАУ 2 = 4. Для знаходження базисних векторiв простору розвтАЩязкiв надамо вiльним невiдомим х3, х4, х5, х6 значення: а) 1, 0, 0, 0; б) 0, 1, 0, 0; в) 0, 0, 1, 0; г) 0, 0, 0, 1. Одержимо чотири вектори, що утворять базис L: е1 = (14, тАУ7, 1, 0, 0, 0); е2 = (тАУ7, 2, 0, 1, 0, 0); е3 = (3, тАУ1, 0, 0, 1, 0); е4 = (тАУ1, тАУ2, 0, 0, 0, 1). У такий спосiб L = ℒ(е1, е2, е3, е4), i будь-який розвтАЩязок вихiдноi системи може бути записаний у виглядi лiнiйноi комбiнацii базисних векторiв, тобто у виглядi: с1(14, тАУ7, 1, 0, 0, 0) + с2(тАУ7, 2, 0, 1, 0, 0) + с3(3, тАУ1, 0, 0, 1, 0) + с4(тАУ1, тАУ2, 0, 0, 0, 1), де с1, с2, с3, с4 тАУ будь-якi значення. Це i i загальний розвтАЩязок вихiдноi лiнiйноi однорiдноi системи рiвнянь.

Задача 7. РозвтАЩязати систему лiнiйних неоднорiдних рiвнянь

РозвтАЩязання. Розширена матриця системи рiвнянь маi вигляд: 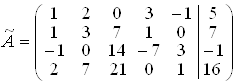, причому до вертикальноi риски записана головна матриця системи, а пiсля вертикальноi риски тАУ стовпець вiльних членiв. Перетворюючи матрицю Вааналогiчно до того, як перетворювалася матриця А в розвтАЩязку попередньоi задачi, одержимо матрицю А таку, що rang = rangА = 2 i . Звiдси можна записати загальний розвтАЩязок системи у виглядi: х1 = 1 + 14х3 тАУ 7х4 тАУ 3х5, х2 = 2 тАУ 7х3 + 2х4 тАУ х5, де х3, х4, х5 тАУ будь-якi.

Це i i загальний розвтАЩязок вихiдноi системи лiнiйних рiвнянь. Однак з метою прояснення алгебраiчноi структури розвтАЩязку системи вiдзначимо таке:

Враховуючи, що rang = rang A = 2 < = 5, можемо зазначити, що множина розвтАЩязкiв системи являi собою лiнiйний многовид. Вектором зсуву цього лiнiйного многовиду i частинний розвтАЩязок неоднорiдноi системи рiвнянь, для знаходження якого дамо вiльним невiдомим х3, х4, х5 довiльнi значення (наприклад нулi) i одержимо: f = (1, 2, 0, 0, 0). Пiдпростором зсуву i простiр розвтАЩязкiв однорiдноi системи з матрицею А2, яка збiгаiться з головною матрицею вихiдноi системи неоднорiдних рiвнянь

Ва.

Звiдси х1 = 14х3 тАУ 7х4 тАУ 3х5, х2 = тАУ 7х3 + 2х4 тАУ х5, де х3, х4, х5 тАУ будь-якi. Даючи вiльним змiнним х3, х4, х5 значення: а) 1, 0, 0; б) 0,1,0; в) 0, 0, 1; одержимо, вiдповiдно, базиснi вектори простору L розвтАЩязкiв однорiдноi системи рiвнянь: е1 = (14, тАУ7, 1, 0, 0), е2 = (тАУ7, 2, 0, 1, 0), е3 = (тАУ3, тАУ1, 0, 0, 1).

Отже, розвтАЩязки вихiдноi системи утворюють лiнiйний многовид М:

M = {x ½x = f + c1e1 + c2e2 + c3e3}, де c1, c2, c3 тАУ будь-якi,

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы